ИССЛЕДОВАНИЕ ОПЕРАЦИЙ
Текст лекций
Кафедра Технической физики
Екатеринбург
2012
СОДЕРЖАНИЕ
Введение. 5
Глава 1. Задачи исследования операций и их решение. 7
1.1. Предмет исследования операций. 7
1.2. Основные понятия и методы исследования операций. 9
1.3. Многокритериальные задачи и системный анализ. 14
Глава 2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ. 20
2.1. Примеры задач линейного программирования. 20
2.2. Общая задача линейного программирования. 22
2.3. Алгебра линейного программирования. 23
2.3.1. Операции над матрицами. 23
2.3.2. Система алгебраических уравнений. 24
2.4. Геометрия линейного программирования. 27
2.5. Идея симплекс-метода. 29
2.6. Алгебра симплекс-метода. 31
2.7. Правила работы с симплекс-таблицей. 35
2.8. Применение ЭВМ.. 42
2.9. Поиск допустимого базисного решения. 45
2.10. Понятие двойственности в линейном программировании. 47
2.11. Целочисленное программирование. 50
2.12. Транспортная задача. 52
2.13. Распределительный метод. 54
2.14. Метод потенциалов. 60
Глава 3. Основы нелинейного программирования.. 62
3.1. Особенности задач линейного программирования. 62
3.2. Методы безусловной оптимизации. 63
3.2.1. Метод покоординатного спуска. 68
3.2.2. Градиентный метод. 69
3.2.3. Метод Ньютона. 73
3.2.4. Минимизация квадратичной формы.. 75
3.2.5. Методы нулевого порядка. 76
3.2.5.1. Метод случайного поиска. 77
3.2.5.2. Метод деформируемого многогранника. 78
3.3. Методы учёта ограничений в форме равенств. 79
3.3.1. Метод прямой оптимизации. 80
3.2.2. Метод приведенного градиента. 80
3.3.3. Метод неопределенных множителей Лагранжа. 82
3.3.4. Пример решения задачи нелинейного программирования. 83
3.4 Учет ограничений в форме неравенств. 86
3.4.1 Теорема Куна-Таккера. 87
3.4.2 Методы решения общей задачи нелинейного программирования. 90
Глава 4. Основы динамического программирования.. 93
4.1. Метод динамического программирования. 93
4.2. Основное уравнение динамического программирования. 96
4.4. Методика решения задач. 103
Глава 5. Марковские случайные процессы.. 106
5.1. Понятие о марковском процессе. 106
5.2. Уравнения Колмогорова для вероятностей состояний. 109
Глава 6. Статистическое моделирование случайных
процессов.. 116
6.1. Метод статических испытаний. 116
6.2. Методы формирования случая. 118
6.3. Пример моделирования случайного процесса методом Монте-Карло. 121
Глава 7. Игровые методы выбора решений.. 126
7.1. Предмет теории игр. 126
7.2. Основные критерии теории игр. 129
7.3. Решение игр в смешанных стратегиях. 133
7.4. Решение игр n×m. 136
ОСНОВНАЯ ЛИТЕРАТУРА.. 139
Введение
Одной из задач, которые всегда и во всех сферах своей деятельности приходится решать человеку, является принятие решений. Постоянная необходимость поиска решений сопровождает всю историю человека.
В любые времена люди, приступая к своим делам, раздумывали над их организацией и выбирали те или другие способы осуществления задуманного мероприятия. Обычно решения принимались без глубокого анализа на основе опыта, интуиции и здравого смысла.
И сегодня при решении бытовых вопросов и принятии решений человек обходится без специальных расчётов, опираясь на те же рычаги. Ошибки в выборе наилучших вариантов здесь приводят к ущербам, касающимся только одного человека или небольшого круга людей.
Однако в производственной деятельности при управлении сложными технологическими процессами здравого смысла и интуиции при поиске наилучших решений уже не хватает и требуется более обоснованный и ответственный подход, ибо ошибки в этом случае могут привести к тяжёлым последствиям.

Для анализа решений на этапе выбора их целесообразно привлекать математическую науку, что позволит ускорить процесс выбора и избежать негативных последствий от неудачных решений.
Наибольшие трудности возникают, когда необходимо планировать новые мероприятия, опыта проведения которых ещё не существует, и опереться здравому смыслу не на что. Здесь только расчёты помогут избежать ошибок в выборе решений.
Очевидно, чем сложнее производственная система и чем больше вкладывается в развитие её материальных ресурсов, тем менее допустимы решения, принимаемые волевым путём без опоры на научные методы и расчёты.
Это в первую очередь относится к энергетике, наиболее сложной и капиталоёмкой производственной системе, от надёжности и экономичности которой зависит работа всех отраслей промышленности, сельского хозяйства и условия жизни людей.
Современные математические методы, облегчающие людям поиск наилучших решений, и являются предметом науки «Исследование операций». Это сравнительно молодая наука. Её возникновение относится к периоду второй мировой войны, когда в армиях США и Англии были сформированы научные группы для принятия решений по организации боевых операций.
В настоящее время исследование операций – одна из самых быстро развивающихся наук, которая находит всё более обширные области применения: промышленность, сельское хозяйство, транспорт, торговля и т. д.
Для решения практических задач в исследовании операций используется целый ряд разделов прикладной математики, среди которых математические методы оптимизации, теория случайных процессов, теория массового обслуживания, теория игр и многие другие.
Из всего многообразия методов здесь будут рассмотрены только наиболее простые и распространённые методы исследования операций.
Глава 1. Задачи исследования операций и их решение
1.1. Предмет исследования операций
Сегодня трудно найти такую область практической деятельности человека, где бы не применялись в разной степени математические модели и методы исследования операций.
Чтобы получить представление о специфике этой науки, рассмотрим ряд типичных для неё задач. Эти задачи, хотя и рассматриваются в упрощённой постановке и взяты из разных предметных областей, имеют практический интерес и дают представление о том, каков предмет и каковы цели исследования операций.
1. Планирование развития энергосистемы. Имеется ряд площадок для сооружения электростанций, необходимых для снабжения электроэнергией новых потребителей. Известны удельные затраты на сооружение электростанций и транспорт электроэнергии. Надо так выбирать тип и мощность блоков, чтобы покрыть дефицит мощности при минимальных затратах.
2. Определение оптимального режима тепловой электрической станции. Имеется ТЭС с заданным составом работающих блоков и известной суммарной нагрузкой, определяемой диспетчером энергосистемы. Необходимо так распределить нагрузку между блоками ТЭС, чтобы обеспечить диспетчерский график выдачи мощности с минимальным расходом топлива.
3. Раскрой металлических полос. При производстве комплектных распределительных устройств требуются отрезки шин нескольких размеров, которые нарезаются из алюминиевых или медных полос различной длины. Необходимо так раскроить имеющиеся полосы, чтобы укомплектовать максимальное число устройств, и свести до минимума обрезки.
4. Планирование производства. Предприятие выпускает трансформаторы разных типов, продажа которых даёт различную прибыль. При производстве используются различные материалы: медный или алюминиевый провод, трансформаторное железо, изоляция и другие материалы, запасы которых известны. Необходимо так спланировать производство, чтобы при имеющихся ресурсах обеспечить максимальную прибыль.
5. План снабжения предприятий сырьем. Имеется ряд предприятий, использующих известные виды сырья, и есть несколько сырьевых баз, которые могут поставлять это сырьё предприятиям. Базы связаны с потребителями имеющимися путями сообщения разных типов известными тарифами. Требуется найти такой план снабжения предприятий сырьём, в котором затраты на транспорт были бы минимальными.
6. Задачи о пищевом рационе. Имеется несколько видов продуктов питания с известной стоимостью каждого. Требуется составить из этих продуктов пищевой рацион, который должен содержать определённое количество различных составляющих (белки, жиры, углеводы и т. п.), необходимых для сбалансированного питания. Рацион должен обеспечить минимальные затраты.
7. Задача о перехвате самолёта противника. Нарушено воздушное пространство страны. Группа истребителей поднята в воздух для перехвата одиночного самолёта противника. Цель операции – сбить самолёт.
Подобных примеров можно привести гораздо больше, но и этих достаточно, чтобы отметить общие черты наиболее популярного класса задач исследования операций. В каждом из примеров речь идёт о мероприятии, имеющем определённую цель. При этом известны некоторые условия и параметры, характеризующие обстановку, с учётом которых требуется принять такое решение, при котором мероприятие будет осуществлено наиболее эффективным способом.
Под эффективностью операции понимают степень выполнения поставленной цели. Чтобы судить об эффективности операции и сравнивать между собой различные планы организации её, нужно иметь определённый численный критерий или показатель эффективности. В рассмотренных примерах это в основном затраты, реже – прибыль.
Некоторые операции, например рассмотренные в последнем примере, содержат элементы случайности. В этих случаях исход операции и эффективность её оценивается вероятностью достижения цели, например, поражения самолёта противника.
Во всех рассмотренных примерах требуется обеспечить минимум или максимум показателя эффективности.
Часто реальные задачи исследования операций наряду с известными, так называемыми детерминированными параметрами, имеющими определённые количественные значения, описываются и неопределёнными, заранее неизвестными факторами.
Наличие неопределённых факторов переводит задачу в область принятия решений в условиях неопределённости. При неизвестных условиях операции нет возможности также успешно оптимизировать решение, как и в случае с детерминированной информацией, и для ожидания в этих условиях хороших решений нет оснований. Один из специалистов по исследованию операций говорил с иронией о своём предмете: «Исследование операций представляет собой искусство давать плохие ответы на практические вопросы, на которые даются ещё худшие ответы другими методами».
Задачи принятия решений в условиях неопределённости встречаются довольно часто. Обычно причиной неопределённости являются погодные условия, покупательский спрос, действия конкурента на рынке и т. п.
Методы исследования операций и предназначены для принятия обоснованных решений во всех рассмотренных ситуациях и им подобных.
1.2. Основные понятия и методы исследования операций
Рассмотрим некоторые термины, основные понятия и принципы исследования операций.
Операцией называют всякое мероприятие или систему действий, объединённое единым замыслом и направленное на достижение определённой цели.
Операция всегда управляемое мероприятие, некоторые параметры которого можно выбирать на этапе планирования мероприятия.
Всякий определённый набор зависящих от нас параметров называется решением. Оптимальными называются решения, в которых обеспечивается максимум или минимум критерия, количественно определяющего эффективность операции.
Для применения математических методов исследования, необходима математическая формализация операции путём формирования математической модели. Как известно, математической моделью операции называют совокупность переменных и систем уравнений и неравенств, которые описывают основные свойства исследуемого объекта и его внутренние и внешние связи, а также целевой функции, формализующей критерий оптимизации.
Требования к математической модели достаточно противоречивы. С одной стороны она должна быть достаточно полной и учитывать все основные свойства рассматриваемой системы. Однако стремление учесть и несущественные обстоятельства может привести к переусложнению модели.
С другой стороны модель должна быть достаточно простой, удобной для анализа математическими методами. Однако подчинение этому требованию может переупростить модель и результаты решения её не будут иметь практического значения.
Искусство составления математических моделей заключается в поиске своеобразной узкой «тропы» между «болотом переусложнения» и «западнями переупрощения». Опыт в составлении моделей приобретается постепенно.
Построение математической модели – наиболее ответственная часть, требующая подчас глубокого понимания свойств моделируемой системы и сущности технологических процессов, происходящих в ней.
Математические модели, применяемые в задачах исследования операций, можно разделить на два класса: аналитические и статистические.
В аналитических моделях свойства системы и зависимости между параметрами описываются с учётом принимаемых допущений формулами в виде линейных и нелинейных алгебраических уравнений. С помощью аналитических моделей удаётся получать удовлетворительные решения для операций с детерминированной информацией.
В сложных операциях, где переплетаются действия многих факторов, включая и случайные, целесообразно использование методов статистического моделирования. Суть этих методов состоит в том, что процесс развития операций «проигрывается» на ЭВМ с учётом всех случайностей, имитируемых с помощью генераторов «псевдослучайных» чисел.
Решение практических задач исследования операций обычно требует комплексного участия специалистов технологов, компетентных в описании предметной области; математиков, хорошо ориентирующихся в современных методах исследования операций; экономистов, способных сформулировать критерии оптимизации, и специалистов по информационным технологиям, ориентирующихся в программном обеспечении современных ЭВМ.
Окончательное принятие решений является компетенцией ответственного лица, обычно заказчика и постановщика задачи, которому предоставлено право окончательного выбора решения. Сокращённо его называют ЛПР – лицо, принимающее решение. При окончательном выборе ЛПР или группа лиц наряду с рекомендациями, вытекающими их анализа математической модели, могут учитывать ряд свойств, которые не удалось формализовать на этапе составления модели.
По результатам анализа решения модели ЛПР может поставить перед исследователями задачу об уточнении или изменении модели. В этом случае процесс исследования операций носит итерационный характер.
В результате решения детерминированной задачи исследования операций находят совокупность параметров, называемых элементами решения, в качестве которых могут фигурировать числа, векторы, функции, состав оборудования, тип его и т. п. Например, в задаче планирования перевозок однотипных грузов от поставщиков к потребителям элементами решения будут числа, определяющие объём груза, перевозимого от i-го поставщика к j-му потребителю. Совокупность чисел, объединяемая в вектор, и образует решение.
Кроме элементов решения, которые являются переменными математической модели, в любой задаче исследования операций имеются ещё и заданные условия, выполнение которых определяет допустимую область решений, называемую «множеством возможных решений».
Задача определения оптимального решения заключается в поиске на множестве возможных решений такого, которое эффективнее других с позиций какого-либо критерия.
Такая задача исследования операций относится к категории обратных задач. Обратные задачи направлены на поиск решения, в котором показатель эффективности достигает своего минимального или максимального значения.
Прямые задачи позволяют определить, что будет, если в заданных условиях мы примем какое-либо решение Х из числа возможных. В первую очередь интересует величина критерия эффективности.
Естественно, прямые задачи значительно проще обратных. Понятно, что для решения обратной задачи надо уметь решать и прямую.
В предлагаемом курсе будут рассматриваться в основном обратные задачи, формулировка которых в самом общем виде приводится ниже.
Пусть имеется некоторая операция, на которую можно влиять, выбирая решение Х, состоящее из группы параметров. Полагаем, что эффективность операции определяется одним показателем W.
Рассмотрим «детерминированный» случай, когда известны условия операции. В этом случае все, влияющие на операции, факторы делятся на две группы: заданные условия выполнения операции, образующие вектор А; элементы решения Х, выбираемые исследователем.
Первая группа факторов определяет допустимую область решений D.
Показатель эффективности – критерий зависит от обеих групп факторов и определяется функцией ![]() .
.
Обратная задача формулируется следующим образом.
При заданном множестве условий А найти такое решение ![]() , которое обеспечивает экстремум показателя эффективности
, которое обеспечивает экстремум показателя эффективности
![]() .
.
Таким образом, задача исследования операций формулируется как типичная математическая задача нахождения максимума или минимума функции ![]() на множестве допустимых решений, определяемом вектор-функцией
на множестве допустимых решений, определяемом вектор-функцией 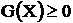 .
.
 Эта задача принадлежит к классу задач математического программирования.
Эта задача принадлежит к классу задач математического программирования.
Характерной особенностью задач исследования операций является алгоритм решения, показанный на рис 1.1.
Задачи ИО всегда порождаются реальной человеческой деятельностью, что и отражается в блоке 1.
Для использования современных методов математики и технических средств обработки информации обязательна математическая формализация, описывающая основные свойства объекта исследования и его связи.
Важное значение имеет также определение целей функционирования системы и формирование функции, позволяющей качественно оценить эффективность решения.
При составлении модели учитывается ориентация на выбранный математический метод оптимизации.
И, наконец, выполняется решение задачи на ЭВМ с последующим анализом его и реализацией на реальном объекте.
1.3. Многокритериальные задачи и системный анализ
При планировании мероприятий по развитию больших и сложных технических или любых других систем часто возникают затруднения с оценкой эффективности и формализацией её в виде функции цели.
Оказывается одним критерием оценить многообразие целей функционирования системы удаётся далеко не всегда.
Например, планируется работа энергетической системы. Какие цели необходимо учитывать при выборе решения? Прежде всего хотелось бы максимально увеличить выработку электроэнергии на электростанциях системы, получить наибольший чистый доход от продажи тепловой и электрической энергии, снизить себестоимость, обеспечить показатели качества отпускаемой продукции, свести до минимума ущерба от перерывов электроснабжения. При глубоком осмысливании задачи могут возникнуть ещё и другие критерии.
Многокритериальность, из которых одни критерии следует обратить в максимум, а другие в минимум, характерна для большинства задач исследования операций.
В этих условиях невозможно найти решение, удовлетворяющее одновременно всем критериям. Решение, обеспечивающее максимальную выработку на тепловых электростанциях, не обращает в минимум вредное влияние выбросов на экологию. Не является, например, корректным лозунг времён плановой экономики «Больше продукции при меньших затратах».
Как выбрать решение в таких ситуациях. Чаще всего решения принимаются на основе использования предшествующего опыта и интуиции. Обычно обеспечить выполнение разных целей невозможно и приходится жертвовать полным обеспечением одних во имя выполнения других, т. е. принимать компромиссные решения.
В проблеме поиска компромиссных решений важную роль играет понятие множества Парето-оптимальных решений. Это множество используется в тех случаях, когда разные критерии несопоставимы и улучшение решения по одному критерию обязательно ухудшает хотя бы один другой критерий. Каждое решение, принадлежащее множеству Парето, лучше других по одним критериям и хуже по другим.
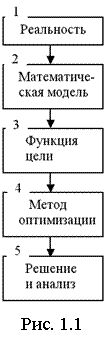
Для примера рассмотрим операцию, которая оценивается двумя противоречивыми критериями, один из которых – затраты S минимизируется, а другой – прибыль W требуется максимизировать.
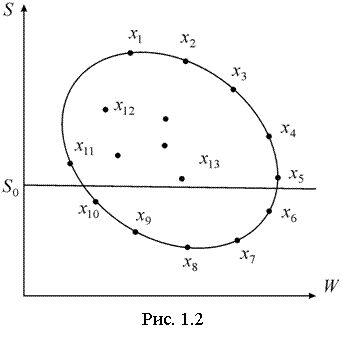 Пусть всё множество допустимых решений образует область, на которой показано несколько возможных решений xi в координатах W и S (рис. 1.2).
Пусть всё множество допустимых решений образует область, на которой показано несколько возможных решений xi в координатах W и S (рис. 1.2).
Решения, лучшие по прибыли лежат на правой границе допустимой области, образуя множество M1, в которое входят варианты ![]() .
.
Решения, лучшие по затратам, лежат на нижней границе, образуя множество M2 с вариантами 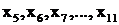 .
.
Парето-множество образуется пересечением ![]() и включает решения
и включает решения![]() , среди которых лучшее по прибыли –
, среди которых лучшее по прибыли – ![]() , лучшее по затратам –
, лучшее по затратам – ![]() и решения с промежуточными показателями.
и решения с промежуточными показателями.
Совершенно очевидно, что дальнейший поиск на основе каких-либо математических или эвристических процедур следует проводить на множестве Парето.
Задача лица, принимающего решение, отдать предпочтение одному из этих вариантов ![]() или выбрать компромиссный –
или выбрать компромиссный – ![]() , взяв на себя ответственность за окончательный выбор.
, взяв на себя ответственность за окончательный выбор.
Рассмотрим некоторые возможные формальные процедуры, позволяющие выбирать решения на множестве Парето.
Самая естественная процедура заключается в формировании некоторого обобщённого показатели эффективности, в котором каждый критерий Wi участвует со своим весовым коэффициентом ![]() , отражающим его важность:
, отражающим его важность:
![]()
Этот показатель формируется по правилам вычисления скалярного произведения двух векторов, что и послужило основанием для названия процедуры методом скаляризации. Коэффициенты важности ![]() определяются обычно экспертным путём.
определяются обычно экспертным путём.
Существует ещё один путь, называемый методом предпочтительного критерия, позволяющий привести задачу к однокритериальной. Здесь выделяется один главный критерий, например ![]() , а все остальные учитываются в виде ограничений, дополняющих математическую модель.
, а все остальные учитываются в виде ограничений, дополняющих математическую модель.
Например, в рассмотренном примере (см. рис. 1.2) можно максимизировать прибыль, наложив ограничения на затраты ![]() , что позволит однозначно выбрать в качестве наилучшего решение
, что позволит однозначно выбрать в качестве наилучшего решение ![]() .
.
Для поиска компромиссного решения может использоваться ещё один приём, названный методом последовательных уступок. Здесь все критерии ![]() ,
, ![]() располагаются в порядке убывания важности, например
располагаются в порядке убывания важности, например ![]() ,
, ![]() и т. д. Сначала ищется наилучшее решение по критерию
и т. д. Сначала ищется наилучшее решение по критерию ![]() , например,
, например, ![]() .
.
Затем назначается на основе опыта, исходя их практических соображений, с учётом малой точности исходных данных, некоторая уступка ![]() , которую можно допустить для того, чтобы оптимизировать второй критерий
, которую можно допустить для того, чтобы оптимизировать второй критерий ![]() :
:
![]() при
при ![]() .
.
При любом методе поиска наилучшего решения на множестве Парето задача сводится к оптимизации по одному критерию, что открывает широкие возможности для применения соответствующих математических методов поиска оптимальных решений, разработанных для однокритериальных задач.
Однако и переход к однокритериальной оптимизации не упрощает задачу выбора оптимальных решений для сложных технико-экономических систем, к которым относится и энергетика. Такие системы с позиций управления относят к большим системам.
Анализ больших систем возможен только на основе системного подхода.
Системный подход опирается на признание объективного характера всеобщей связи, причинной обусловленности явлений, господства необходимости, правильного сочетания необходимости и случайности [8]. Методология системного подхода опирается на следующие главные положения:
1) окружающая действительность должна изучаться в единстве, целостности и развитии;
2) наши знания окружающей действительности всегда относительны, ибо они отражают неполную информацию о событиях, явлениях и свойствах системы;
3) в природе и в обществе всегда прослеживаются причинно-следственные связи, которые являются проявлением объективных законов развития природы.
Системный подход реализуется путём сочетания следующих принципов исследования:
· система должна рассматриваться как единое целое;
· система всегда, с одной стороны, находится в окружении других систем разных типов и испытывает на себе их влияние, с другой стороны, она находится на некотором уровне иерархии систем данного типа и её управление также обладает свойствами иерархичности;
· в основе оптимизации должны лежать предварительно и достаточно чётко сформулированные цели функционирования системы;
· оптимизационная модель системы должна учитывать все определяющие свойства системы, а также связи с другими системами и окружающей средой;
· полученное решение в ходе его реализации должно корректироваться и дополняться с учётом вновь появляющихся обстоятельств и уточнений информации.
Инструментом реализации системного подхода при исследовании больших систем является системный анализ. Системный анализ предполагает, что для получения решения необходимо выполнить следующие основные этапы исследования.
1. Постановка задачи, заключающаяся в выборе исследуемой системы, локализации её, т. е. определении границ и связей с соседними системами, формулировке целей управления.
2. Составление математической модели, т. е. формализация внутренних свойств системы и её внешних связей, формирующих систему ограничений ![]() и целевой функционал
и целевой функционал ![]() .
.
3. Выбор метода решения модели, ориентация на который должна учитываться и при составлении математической модели.
4. Решение модели на ЭВМ и определение по полученным результатам возможных оптимальных путей развития системы в зависимости от управляющих возможностей.
5. Планирование оптимального развития системы постановщиком задачи – лицом принимающим решение или группой лиц с учётом полученных в результате решения рекомендаций, а также тех обстоятельств, которые не были формализованы при разработке математической модели.
В процессе системного анализа важное значение имеет согласованность математической модели и методов её решения. Разработка модели и выбор метода решения всегда выполняются совместно и согласованно.
Вопросы составления математических моделей для энергетических систем и их объектов будут рассматриваться позже в специальном курсе «Модели оптимального развития энергосистем и САПР».
Изложение сведений по методам оптимизации будет проведено в следующих главах учебного пособия.
Задача однокритериальной оптимизации математически записывается предельно компактно
![]() при
при ![]() ,
,
где Х – вектор неизвестных параметров,
F – целевой функционал,
![]() – вектор-функция ограничений, определяющая допустимую область решений.
– вектор-функция ограничений, определяющая допустимую область решений.
Методы оптимизации в математической науке разработаны достаточно полно и составляют целый раздел прикладной математики, называемый «Математическое программирование», хотя используемый здесь термин и не имеет никакого отношения к теории программирования.
Изучение методов оптимизации начнём с простейшей линейной оптимизации.
Глава 2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
2.1. Примеры задач линейного программирования
В линейном программировании функции F(X) и g(X) описываются линейными выражениями, например:
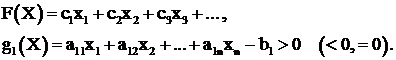 (2.1)
(2.1)
Многие практические задачи достаточно точно могут быть описаны как линейные.
Пример 1. Планирование рациона. Для обеспечения сбалансированного питания необходимо обеспечить суточные потребности организма в белках, жирах и углеводах. На выбор имеются четыре продукта питания: П1, П2, П3, П4. Известны стоимость каждого продукта Сi, (i = 1, 2, 3, 4) и суточная потребность в белке В1, углеводах В2 и жирах В3. Содержание этих составляющих в каждом продукте аi1, ai2, ai3, ai4 образует матрицу
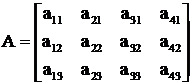 .
.
Необходимо определить такой рацион, который обеспечит потребности в белках, жирах и углеводах при минимальных затратах.
Составим математическую модель:
1) обозначим через х1, х2, х3, х4 неизвестные объемы продуктов питания,
2) опишем ограничения: 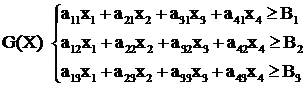 , (2.2)
, (2.2)
3) целевая функция: F(X) = с1х1 + с2х2 + с3х3 + с4х4 → min.
В задаче требуется найти такое неотрицательное решение (![]() ), которое удовлетворяет ограничениям и обеспечивает минимум F(X).
), которое удовлетворяет ограничениям и обеспечивает минимум F(X).
Пример 2. Планирование производства. На предприятии, выпускающем провода марки АС-70, АС-95, АС-120 и АС - 150 имеются две группы установок: первого типа в количестве N1 и второго – N2. Каждая установка может выпускать любой провод из этой номенклатуры, но с разной производительностью aij, заданной в табл. 2.1.
Таблица 2.1
j i | АС-70 | АС-95 | АС-120 | АС-150 |
1 | а11 | а12 | а13 | а14 |
2 | а21 | а22 | а23 | а24 |
Известна прибыль от реализации 1 км каждого типа провода: с1, с2, с3, с4.
Задан плановый выпуск каждого типа провода: b1, b2, b3, b4.
Считается также, что все установки должны быть в работе и заданный план можно перевыполнять.
Необходимо распределить производство проводов между установками таким образом, чтобы обеспечить максимальную прибыль.
Математическая модель:
1) хij – число станков i-го типа, выделяемых на выпуск каждого j-го провода:
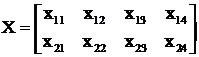 .
.
2) Условие по количеству установок: |
|
и условие выполнения плана: |
|
3) Целевая функция:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |



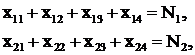 (2.3)
(2.3)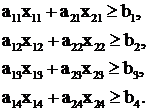 (2.4)
(2.4)