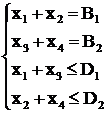 . (2.30)
. (2.30)
В качестве целевой функции принимаем грузопоток
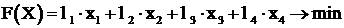 .
.
Полученную задачу линейного программирования приведём к каноническому виду, т. е. перейдем от неравенств к равенствам:
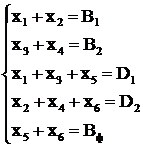 (2.31)
(2.31)
Для системы условий задачи имеем n = 6, m = 5.
Проанализируем полученную систему условий задачи с целью определения ранга. Одно из уравнений системы является линейно зависимым, так как для них можно найти условие, например,
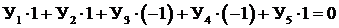 ,
,
где Уi – уравнение с номером i.
Значит ранг системы R = 4, и в оптимальном решении должно быть только 4 базисных переменных.
В общем случае R = N + M для открытой задачи и R = N + M – 1 для закрытой задачи, где N, M – число поставщиков и потребителей.
Для решения транспортной задачи может использоваться симплекс-метод. Однако существует несколько более простых методов решения её, из которых рассмотрим два метода: распределительный метод и метод потенциалов.
2.13. Распределительный метод
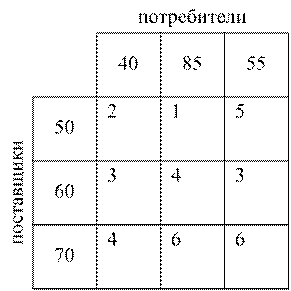
Суть метода рассмотрим на примере, в котором участвуют 3 потребителя и 3 поставщика. Запасы, потребности в тоннах и расстояния в км заданы в табл. 2.9.
Решение начинается с составления допустимого базисного решения, называемого опорным планом. Он должен иметь 5 базисных, т. е. не равных нулю переменных.
Таблица 2.9 Таблица 2.10
|
|
Задача является закрытой, так как 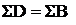 и
и 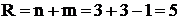 .
.
Решение начинается с составления допустимого базисного решения, называемого опорным планом. Он должен иметь 5 базисных, т. е. не равных нулю переменных.
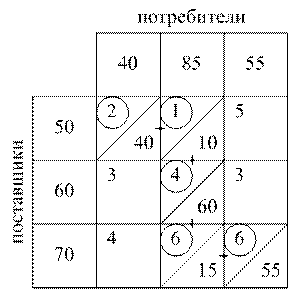
Составить опорный план можно разными методами. Применим так называемый метод северо-западного угла. Левую верхнюю клетку (путь от первого поставщика до первого потребителя) загружаем по максимуму, т. е. планируем перевозить по этому пути столько, сколько надо потребителю или сколько может дать поставщик. Если первому потребителю не хватило продукта – загружаем соседнюю клетку и т. д. Полученный опорный план представлен в табл. 2.10. Значение целевой функции
![]() .
.
Даже поверхностный взгляд на опорный план показывает, что неудачно загружено направление длиной 1 км. Очевидно, этот путь надо загрузить более полно.
Для оценки ожидаемого эффекта загрузим эту клетку на 1 т, что вызовет необходимость разгрузки на 1 т клетки слева, чтобы запас у поставщика не изменился. Поскольку потребности потребителей также не должны изменяться, поэтому нужно загрузить на 1 т клетку 3 км и разгрузить на 1 т клетку 4 км. Таким образом, в перераспределении поставок была рассмотрена цепочка, показанная на рис. 2.14.
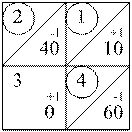
Рис. 2.14
Цепь – всегда замкнутый многоугольник с четным числом вершин, только одна из которых не имеет поставки.
Для оценки эффекта найдем изменение целевой функции при перераспределении поставок на 1 т в рассматриваемой цепочке, характеризующее клетку без поставки: 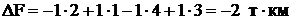 .
.
Этот показатель для цепочки называют характеристикой, обозначаемой 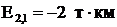 .
.
Перераспределение по всем клеткам цепочки проводится на одинаковую величину, а объем перераспределения определяется минимальной поставкой в клетке, где поставки уменьшаются. Очевидно после перераспределения там окажется 0. В нашем случае уменьшаются поставки в клетках 2/40 и 4/60. Следовательно, объем перераспределения поставок – 40 т (рис. 2.15). Целевая функция при этом изменится на 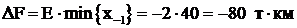 и для полученного плана составит
и для полученного плана составит ![]() .
.

Рис. 2.15
Улучшенный новый план по результатам проведённого перераспределения показан в табл. 2.11.
Таблица 2.11
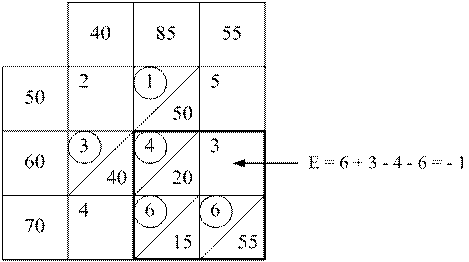
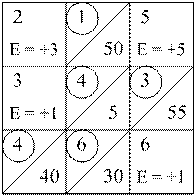
Аналогично произведем дальнейшую оптимизацию плана. Результаты последовательного улучшения плана поставок показаны в табл. 2.12, 2.13 и 2.14.
Таблица 2.12 Таблица 2.13 Таблица 2.14
|
|
|
(*) |
|
|
Чтобы убедиться в оптимальности полученного плана, необходимо определить характеристики для всех «пустых» клеток, для которых они должны быть положительными.
При реализации распределительного метода возникают следующие самостоятельные задачи, связанные с построением опорного плана и определением цепочек для «пустых» клеток. Опорный план должен иметь число «занятых» клеток (кружков), равное рангу системы, и эти кружки должны образовывать вычёркиваемую комбинацию.
Эта комбинация проверяется последовательным вычеркиванием кружков, которые являются единственными в строке или в столбце. На рис. 2.16 показаны два опорных плана, из которых второй не отвечает этим требованиям.
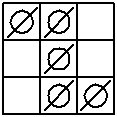
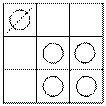
Рис. 2.16
Формирование опорного плана может проводиться одним из следующих методов:
– метод северо-западного угла;
– метод минимального элемента в столбике;
– метод минимального элемента в строке;
– метод минимального элемента в таблице.
Из них наиболее эффективным является последний метод из этого списка.
При определении цепочек следует иметь ввиду, что в больших задачах они могут быть много сложнее, чем в рассмотренном примере. На рис. 2.17 показаны возможные виды цепочек.
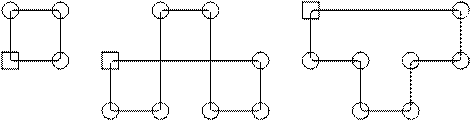
Рис. 2.17
Алгоритм определения цепочек строится на основе проверки вычеркиваемой комбинации кружков (клеток с поставками).
При определении цепочки для какой-либо «пустой» клетки искусственно записывают в неё кружок, затем последовательно вычеркивают все кружки, являющиеся единственными в своей строке или столбце. Оставшиеся от вычеркивания кружки образуют вершины многоугольника цепочки.
В качестве примера найдем цепочку с использованием вычеркиваемой комбинации для плана, получившегося после второго улучшения в рассмотренном ранее примере (рис. 2.18), где показана последовательность вычеркивания.

Рис. 2.18
При составлении опорного плана может оказаться, что число базисных переменных меньше ранга R. Этот случай называют «вырождением». Для устранения его в опорный план вводят искусственную поставку, равную нулю, выбрав для неё любую клетку, не вызывающую образования цепочки.
Характеризуя в целом распределительный метод, следует отметить его достоинство – простоту, дающую возможность вручную решать сложные задачи.
Недостаток метода заключается в необходимости рассмотрения большого числа цепочек.
2.14. Метод потенциалов
Этот метод позволяет определять характеристики клеток без построения цепочек. Для этого используются потенциалы – некоторые показатели поставщиков vi и потребителей uj, которые определяются по следующему правилу: сумма потенциалов поставщика и потребителя должна быть равна показателю клетки, которая их связывает и по которой запланирован транспорт продукта,
![]() , (2.32)
, (2.32)
где ![]() – показатель перевозок клетки с кружком, т. е. с запланированной поставкой, которая связывает i-го поставщика и j-го потребителя.
– показатель перевозок клетки с кружком, т. е. с запланированной поставкой, которая связывает i-го поставщика и j-го потребителя.
Один из потенциалов в опорном плане может приниматься произвольно. Найдем потенциалы (табл. 2.15) для первого опорного плана в рассмотренном ранее примере.
Таблица 2.15
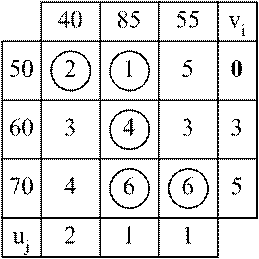
Потенциал первого поставщика выберем произвольно ![]() .
.
Остальные потенциалы найдем по условию (2.32) в следующей последовательности:
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() .
.
Потенциалы имеют определённый экономический смысл, определяемый затратами 3-х субъектов: поставщика, потребителя и транспортной компании. При этом потенциалы можно рассматривать как транспортные издержки компании βij, которые в принятом плане компенсируются потребителем и поставщиком в объемах, соответственно, uj и vi.
Определим способ расчета характеристики с помощью потенциалов. Ранее была получена характеристика клетки, лежащей на пересечении 2-й строки и 1-го столбца ![]() . Найдем ее с помощью потенциалов:
. Найдем ее с помощью потенциалов:
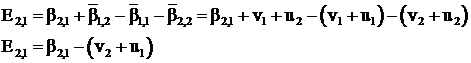 , (2.33)
, (2.33)
Таким образом, характеристика клетки без поставки определяется как разность показателя перевозок и суммы потенциалов поставщика и потребителя, которых связывает рассматриваемая клетка:
![]() .
.
Использование потенциалов позволяет более просто, без построения цепочек найти клетки, в которых целесообразно ввести поставку. Однако для связанной с этим последующей корректировки плана будет необходимо найти цепочку и провести перераспределение поставок в её вершинах.
Глава 3. Основы нелинейного программирования
3.1. Особенности задач линейного программирования
Математически задача нелинейного программирования формулируется следующим образом:
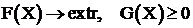 , (3.1)
, (3.1)
где ![]() – вектор переменных,
– вектор переменных,
F(X) – целевая функция,
![]() – вектор-функция ограничений, которые могут иметь форму равенств и неравенств.
– вектор-функция ограничений, которые могут иметь форму равенств и неравенств.
 В нелинейном программировании
В нелинейном программировании ![]() или хотя бы одна функция
или хотя бы одна функция ![]() должна быть нелинейной. Появление нелинейностей накладывает целый ряд особенностей на задачу. Основные из них:
должна быть нелинейной. Появление нелинейностей накладывает целый ряд особенностей на задачу. Основные из них:
· Допустимая область может быть невыпуклой, как например для системы из двух следующих ограничений (рис. 3.1)
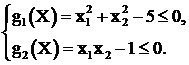 (3.2)
(3.2)
· Решение задачи может лежать как внутри, так и на границе допустимой области.
· Целевая функция может иметь несколько экстремумов, среди которых различают локальные А, С и глобальные В (рис.3.2).
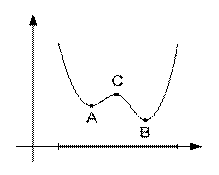
Рис. 3.2
В отличии от линейного программирования в нелинейном существуют десятки методов, ориентированных на надёжную работу в конкретных условиях, и практически не существует универсального метода, который позволяет решать любые задачи. Ниже будут рассмотрены лишь основные методы. При изложении материала иллюстрация методов будет проводиться для функции двух переменных ![]() , представленной на плоскости в координатах
, представленной на плоскости в координатах ![]() линиями равных значений
линиями равных значений ![]() .
.
Суть такого представления показана на рис. 3.3 для функции
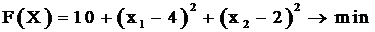 . (3.3)
. (3.3)
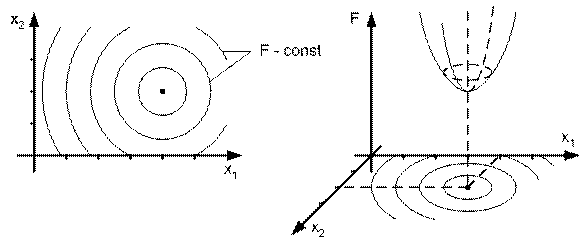
а) б)
Рис. 3.3
Основы нелинейного программирования начнём с изучения методов оптимизации нелинейной функции ![]() , где на допустимую область не накладывается никаких условий.
, где на допустимую область не накладывается никаких условий.
3.2. Методы безусловной оптимизации
Итак, рассмотрим задачу 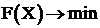 , где
, где 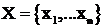 .
.
Из общего курса математики известно, что аналитическое решение задачи определяется равенством нулю всех частных производных
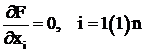
и положительным значением второго дифференциала ![]() .
.
Однако, для решения практических задач обычно используются итеративные методы, ориентированные на реализацию их на ЭВМ. Эти методы делятся на два основных типа – методы перебора и методы возможных направлений.
Метод перебора.
При переборе используется только вычисление значения функции ![]() в различных точках некоторой сетки, определяемых условием:
в различных точках некоторой сетки, определяемых условием:
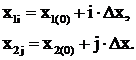 (3.4)
(3.4)
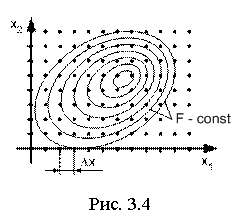 Функция
Функция ![]() вычисляется в каждой точке сетки и затем путем сравнения выбирается минимальное значение ее (рис. 3.4).
вычисляется в каждой точке сетки и затем путем сравнения выбирается минимальное значение ее (рис. 3.4).
Достоинство метода: за счет сканирования всей допустимой области могут решаться задачи с несколькими экстремумами. Недостаток: большой объем расчетов.
 Для сокращения объема вычислений можно использовать метод направленного перебора, который заключается в расчете
Для сокращения объема вычислений можно использовать метод направленного перебора, который заключается в расчете ![]() в соседних точках и переходе в ту их них, где значение функции минимально. Но в этом случае в задаче с несколькими экстремумами можно не найти глобальный.
в соседних точках и переходе в ту их них, где значение функции минимально. Но в этом случае в задаче с несколькими экстремумами можно не найти глобальный.
Методы перебора исполь-зуются редко. Поэтому наибольшее распространение получили методы возможных направлений.
Это разновидность итерационных методов, которые начинаются с произвольно выбранного начального приближения.
В исходной точке Х0 рассматривается несколько направлений (рис. 3.5) для перехода в новую точку Х1. Возможными называют направления, которые ведут в сторону уменьшения целевой функции (направления 1 и 4). Перемещение допускается по любому возможному направлению ![]() в текущей точке пропорционально некоторой константе t, называемой шагом, т. е.
в текущей точке пропорционально некоторой константе t, называемой шагом, т. е.
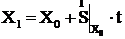 . (3.5)
. (3.5)
В точке Х1 аналогично выбирается возможное направление и делается очередной шаг. Общее уравнение итерационного процесса по методу возможных направлений
![]() . (3.6)
. (3.6)
Величина шага влияет на сходимость вычислительного процесса, определяемую числом итераций: при малых t – процесс сходится, но медленно; при больших t – процесс может расходиться.
Между этими крайностями существует оптимальный шаг, который на принятом направлении приводит в точку минимального значения F, где это направление касается линии ![]() (рис. 3.6)
(рис. 3.6)

Рис. 3.6
Для отыскания оптимального шага tопт можно на принятом направлении ![]() выражение
выражение ![]() подставить в целевую функцию
подставить в целевую функцию ![]() и после преобразований получить новую функцию, зависящую только от шага
и после преобразований получить новую функцию, зависящую только от шага ![]() , а затем найти ее минимальное значение.
, а затем найти ее минимальное значение.
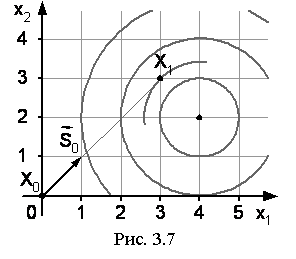
Пример: ![]() , при исходном приближении и заданном возможном направлении:
, при исходном приближении и заданном возможном направлении: ![]() ,
, ![]() .
.
 Значения переменных в конце шага:
Значения переменных в конце шага:
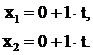
Подставим эти значения в целевую функцию:
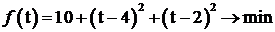 .
.
Запишем условие минимума функции:
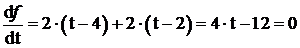 , откуда
, откуда ![]() .
.
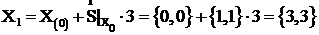
Траектория перехода показана на рис. 3.7.
Зависимость ![]() на принятом возможном направлении далеко не всегда удается найти в аналитическом виде. В этом случае функцию
на принятом возможном направлении далеко не всегда удается найти в аналитическом виде. В этом случае функцию ![]() можно аппроксимировать, например, кривой второго порядка
можно аппроксимировать, например, кривой второго порядка
![]() , (3.7)
, (3.7)
что позволяет определить оптимальный шаг
![]() . (3.8)
. (3.8)
Поиск трех неизвестных коэффициентов а, b, с требует формирования трех уравнений. Для этого рассматриваются 3 точки на принятом направлении для разных значений t, равных, например, t=0, t=1, t=2, и для каждой точки определяется значение целевой функции:
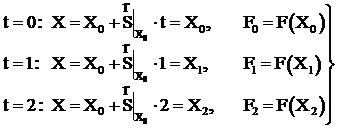 (3.9)
(3.9)
Очевидно, для рассмотренных шагов эти значения должны совпадать с рассчитанными по аппроксимирующей кривой
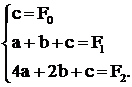 (3.10)
(3.10)
Решение этой системы позволяет найти все неизвестные а, b, с и tопт следующим образом. Исключим с из системы и получим систему из двух уравнений:
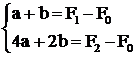 (3.11)
(3.11)
Домножив первое уравнение на –4, затем на –2 и сложив со вторым найдём неизвестные а и b:
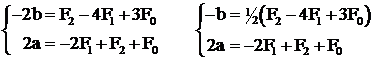
Для оптимального шага получим следующее выражение:
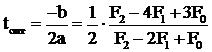 . (3.12)
. (3.12)
В рассмотренном выше примере найдем оптимальный шаг этим методом:
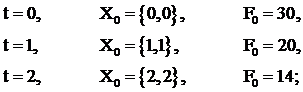
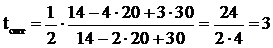 .
.
Методы, в которых определяется оптимальный шаг, называются методами скорейшего поиска. Эти методы широко используются в энергетике, так как позволяют за меньшее число итераций находить оптимальные решения, хотя требуют большего количества вычислений на итерации.
В зависимости от способа определения возможного направления различают несколько методов, которые и рассмотрим далее.
3.2.1. Метод покоординатного спуска
В качестве возможных направлений здесь используются орты, т. е. единичные векторы по всем неизвестным. Оптимизация производится поочередно только по одному орту, начиная с е1. На рис. 3.8 показана траектория оптимизации с использованием скорейшего спуска. В полученной точке Х1 спуск проводится по ![]() и т. д. После оптимизации по
и т. д. После оптимизации по ![]() первый цикл заканчивается.
первый цикл заканчивается.
Очередной цикл проводится аналогично.

Рис. 3.8
Достоинство метода: простой алгоритм, по которому на каждом этапе производится оптимизация только по одной переменой при фиксированных значениях остальных. При этом могут использоваться различные методы одномерной оптимизации по одной переменной, в том числе и метод перебора.
Недостатком метода является не всегда хорошая сходимость. Особенно плохая сходимость отмечается для функций типа «овраг».
3.2.2. Градиентный метод
В этом методе в качестве возможного направления в текущей точке принимается градиент ![]() при поиске максимума, или антиградиент
при поиске максимума, или антиградиент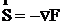 при поиске минимума функции. Градиент, как известно, это вектор, направленный в сторону наибольшего возрастания функции, т. е. по перпендикуляру к касательной линии
при поиске минимума функции. Градиент, как известно, это вектор, направленный в сторону наибольшего возрастания функции, т. е. по перпендикуляру к касательной линии ![]() . На рис. 3.9. показано направление антиградиента.
. На рис. 3.9. показано направление антиградиента.

Рис. 3.9
Основное уравнение градиентного метода при поиске минимума функции
![]() . (3.13)
. (3.13)
При постоянном небольшом шаге t траектория поиска проходит перпендикулярно линиям ![]() . При реализации скорейшего спуска
. При реализации скорейшего спуска
поиск tопт может осуществляться следующим методом, основанным на
определении градиентов в двух точках: в исходной при t=0 и в конце некоторого пробного шага t0.
Действительно, на направлении антиградиента целевая функция F зависит только от величины шага t (рис. 3.10). Но вид ![]() , а тем более
, а тем более ![]() в большинстве случаев невозможно определить.
в большинстве случаев невозможно определить.
Для оценки зависимости ![]() и делается пробный шаг t0, в конце которого определяется величина
и делается пробный шаг t0, в конце которого определяется величина ![]() , соответствующая отрезку cd. Значение
, соответствующая отрезку cd. Значение ![]() в исходной точке определяется отрезком аb.
в исходной точке определяется отрезком аb.

Рис. 3.10
Таким образом, появляется возможность аппроксимировать неизвестную зависимость ![]() прямой, проходящей через две точки. Из подобия треугольников можно определить шаг
прямой, проходящей через две точки. Из подобия треугольников можно определить шаг ![]() , при котором эта прямая проходит через нуль, определяя шаг, не совпадающий с оптимальным, но близкий к нему
, при котором эта прямая проходит через нуль, определяя шаг, не совпадающий с оптимальным, но близкий к нему
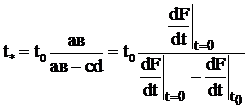 . (3.14)
. (3.14)
Производные ![]() могут быть найдены с учётом неявной зависимости
могут быть найдены с учётом неявной зависимости ![]() , определяемой основным уравнением градиентного метода.
, определяемой основным уравнением градиентного метода.
Например, производная в текущей точке Хk
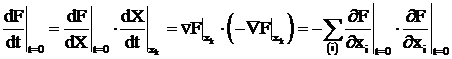 . (3.15)
. (3.15)
Аналогично найдем производную в конце пробного шага
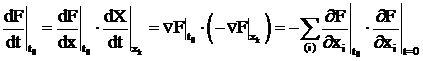 . (3.16)
. (3.16)
В этих выражениях учтено, что произведение градиентов определяется по правилу вычисления скалярного произведения векторов.
Ниже приведён алгоритм градиентного метода с выбором оптимального шага (рис. 3.11). Блоки алгоритма выполняют следующие функции.
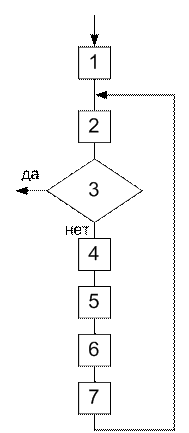 1. Исходное приближение
1. Исходное приближение ![]() .
.
2. Определение градиента в текущей точке ![]() .
.
3. Проверка на заданную точность ![]() .
.
4. Выполнение пробного шага ![]() .
.
5. Определение градиента в конце пробного шага ![]() .
.
6. Определение 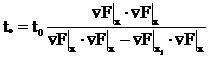
7. Выполнение рабочего шага 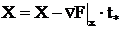 .
.
|
При реализации алгоритма наибольшие затраты времени связаны с определением градиента целевой функции. Как известно, составляющими вектор-градиента ![]() являются частные производные по всем компонентам вектора Х;
являются частные производные по всем компонентам вектора Х;
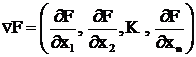 .
.
Все составляющие ![]() определяются легко, если функция F задана аналитически. В практических задачах такое встречается крайне редко. В этом случае используются численные методы определения производных, основанные на конечных приращениях (рис. 3.12).
определяются легко, если функция F задана аналитически. В практических задачах такое встречается крайне редко. В этом случае используются численные методы определения производных, основанные на конечных приращениях (рис. 3.12).
Как известно, производная в точке ![]() определяется наклоном касательной к кривой, т. е. пропорциональна
определяется наклоном касательной к кривой, т. е. пропорциональна ![]() .
.
Определение через конечные приращения подменяет касательную секущей
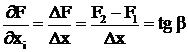 . (3.17)
. (3.17)
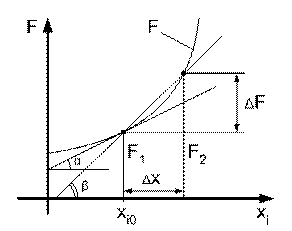
Рис. 3.12
Для уменьшения погрешностей используется метод центрированных приращений, при которых приращение делается вправо и влево от рабочей точки (рис. 3.13)
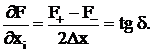 (3.18)
(3.18)
При этом угол δ значительно ближе по величине к углу α, определяющему точное значение производной.
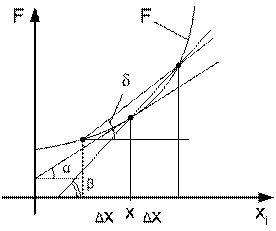
Рис. 3.13
3.2.3. Метод Ньютона
Метод Ньютона относится к методам второго порядка, более сложным по сравнению с градиентным, так как рассматриваемый метод строится на основе производных второго порядка. Как любой итерационный метод и метод Ньютона начинается с исходного приближения Х0.
Рассмотрим суть метода на примере функции только одной неизвестной 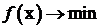 .
.
Разложим ![]() в ряд Тейлора в точке
в ряд Тейлора в точке ![]() с учётом первых слагаемых
с учётом первых слагаемых
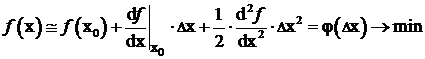 .
.
Такое разложение эквивалентно замене исходной функции параболой в окрестности ![]() (рис 3.14).
(рис 3.14).
Запишем условие минимума функции ![]()
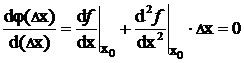 ,
,
откуда найдем отклонение ![]()
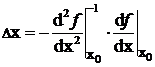 .
.
Новое значение переменной, при котором имеет место минимум функции,
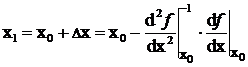 . (3.20)
. (3.20)
В новой точке ![]() выполняются те же вычисления:
выполняются те же вычисления: ![]() заменяется разложением в ряд Тейлора и находится очередная точка
заменяется разложением в ряд Тейлора и находится очередная точка ![]() и т. д.
и т. д.
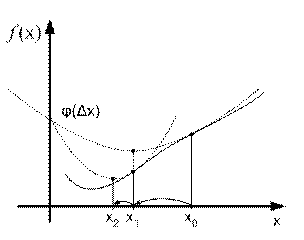
Рис. 3.14
Общее уравнение метода:
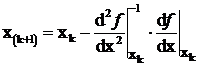 (3.21)
(3.21)
Основное уравнение метода Ньютона для функции многих переменных:
![]() , (3.22)
, (3.22)
где Х – вектор неизвестных,
![]() – вектор-градиент,
– вектор-градиент,
G – матрица вторых производных (матрица Гессе), равная
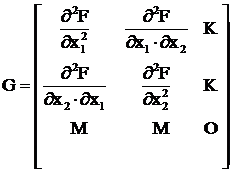 .
.
Матрица Гессе является квадратной, симметричной относительно главной диагонали и имеет обратную матрицу.
Для функции нескольких переменных разложение в ряд Тейлора заменяет её в точке Х0 функцией второго порядка (эллипсоидом), и поиск минимума опускает точку Х в центр эллипсоида.
Метод имеет хорошую сходимость, т. е. малое количество итераций. Платой за это является большой объем вычислений, связанный с формированием матрицы Гессе и её обращением.
Метод Ньютона используется в программах оптимизации режима энергосистем. При этом, учитывая слабую заполненность матрицы G ненулевыми элементами приращение ![]() находят без обращения матрицы Гессе путём решения системы уравнений
находят без обращения матрицы Гессе путём решения системы уравнений
![]() . (3.23)
. (3.23)
3.2.4. Минимизация квадратичной формы
На практике часто встречаются задачи, в которых целевые функции имеют квадратичную форму
![]() . (3.24)
. (3.24)
Поиск минимума функции здесь сводится к поиску решения системы линейных алгебраических уравнений 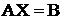 .
.
Действительно, условие минимума функции ![]() , что и определяет решение задачи.
, что и определяет решение задачи.
Проверим справедливость этого положения на примере функции второго порядка.
Итак, имеем квадратичную форму ![]() , в которой
, в которой
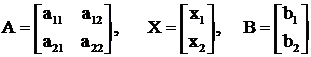 .
.
Целевая функция, преобразованная в алгебраическую форму, будет иметь вид
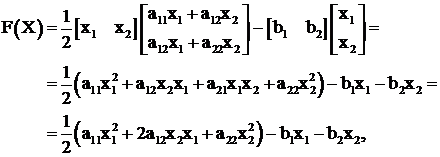
для которой условия минимума функции
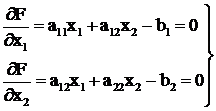
или в матричной форме ![]() .
.
3.2.5. Методы нулевого порядка

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |