Исследование операций (стр. 6 )

Глава 4. Основы динамического программирования

4.1. Метод динамического программирования

В линейном и нелинейном программировании процесс оптимизации считался независящим от времени, т. е. статическим.

Динамическое программирование приспособлено для оптимизации «многошаговых» или «многоэтапных» операций.

Примерами таких операций могут быть распределение инвестиций в предприятие по годам расчётного периода с целью максимизации прибыли; или выбор суточного режима электростанции при ограниченном запасе первичного энергоресурса; или процесс наведения ракеты на цель; или процесс подъёма параметров пара на блоке тепловой электростанции и целый ряд других технико-экономических задач.

Некоторые процессы делятся на шаги естественным образом; в других разделение приходится проводить искусственно.

Эффективность W таких многоэтапных процессов, как правило, складывается из эффектов на отдельных этапах

, (4.1)

где – эффект на i-м этапе.

Такой критерий называют «аддитивным».

Управление операцией проводится на каждом шаге и влияет не только на эффект на шаге, но и на эффективность операции в целом. Вектор управления операцией 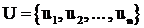должен выбираться так, чтобы обеспечивался максимум эффективности всей операции .

Такое управление называют оптимальным.

Поиск оптимального управления можно проводить, определяя сразу все n шаговых управлений , т. е. решая задачу многомерной оптимизации, либо строить процесс поиска шаг за шагом, оптимизируя на шаге только одно управление . Динамическое программирование ориентировано на второй способ, как более простой.

Но оптимизация на шаге должна проводиться с учётом последствий выбора на все шаги операции, т. е. управление на i-м шаге надо выбирать так, чтобы эффект на этом шаге и на всех последующих до конца операции шагах был максимальным. В особых условиях при этом находится последний шаг процесса, за которым уже нечего учитывать. В связи с этим часто поиск оптимального решения начинают с последнего шага, последовательно этап за этапом приближаясь к началу.

Суть принципа динамического программирования достаточно проста и понятна: управление на каждом шаге должно приниматься так, чтобы оно было продолжением оптимальных управлений, найденных на уже рассмотренных шагах.

Используем этот принцип для поиска кратчайшего пути из пункта А в пункт Б. Дорожная карта, весьма условная, приведена на рис. 4.1, где показана длина дорог в км.

Рис. 4.1

Приступая к решению задачи, необходимо в первую очередь разбить процесс на шаги. В качестве шага примем переход в соседний пункт и наметим возможные состояния операции в конце каждого шага, обозначенные . Начальное и конечное состояния характеризуются пребыванием только в одном пункте, соответственно, А и Б. Возможные состояния в конце первого и четвёртого шага включают по два пункта, и - по три пункта возможных маршрутов.

Управление на каждом шаге заключается в выборе дороги, направленной в меридианальном или широтном направлениях. Эффективность управления определяется длиной пути в км.

Оптимизацию начнём с последнего пятого шага (рис. 4.2). Рассмотрим все возможные состояния, а их два, в начале шага, и для каждого выберем оптимальное управление, ведущее в конечный пункт. Управления здесь выбираются однозначно и запоминаются. Эффект на шаге определяется длиной пути и также запоминается как характеристика соответствующего состояния. На рис. 4.2 оптимальные управления отмечены стрелками, а условно оптимальные эффективности вписаны в кружки.

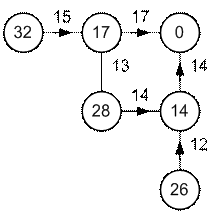
Рис. 4.2

Затем переходят к оптимизации предпоследнего шага. Здесь для каждого состояния в начале шага выберем оптимальное управление, ведущее в конечный пункт. Для первого и третьего состояний управления определяются однозначно. Для среднего состояния из двух возможных управлений выбирается лучшее по кратчайшему пути до конечного пункта. Этот путь определяется суммой пути на шаге, соответственно 13 и 14 км, и условно оптимальных эффектов на последующих шагах, т. е. 17 и 14 км.

Аналогично проводится условная оптимизация на остальных шагах, результаты которой показаны на рис 4.3.

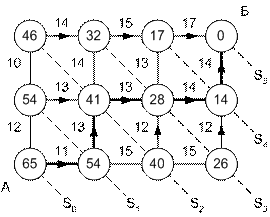
Рис. 4.3

Оптимальная траектория, выделенная толстыми линиями, находится обратным ходом с использованием запомненных условно-оптимальных управлений для каждого состояния.

Процесс условной оптимизации может проводиться аналогично и из начального состояния системы, разворачиваясь от начала к концу.

4.2. Основное уравнение динамического программирования

Формализуем изложенный принцип и идею динамического программирования. С этой целью рассмотрим операцию, заключающуюся в переводе системы из состояния в конечное состояние .

Выделим на рис. 4.4 i-й шаг с состоянием в начале и наметим несколько возможных управлений на шаге и соответствующих им состояний в конце шага, а также наилучших траекторий на всех последующих шагах, найденных на пройденных этапах условной оптимизации, проведённой, начиная с последнего шага.

Введём следующие обозначения: – состояние в начале i-го шага; – состояние в конце шага; – управление на i-м шаге; – эффект на i-м шаге; – условно-оптимальный эффект на всех шагах, начиная с -го до последнего, при условии, что система находится в состоянии .

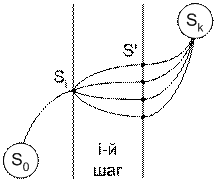
Рис. 4.4

Очевидно, состояние и эффект , зависят от состояния в начале шага и управления на шаге: , .

Определим общий суммарный эффект на i-м шаге при любом управлении на шаге и эффект на всех последующих при оптимальном управлении на этих шагах:

. (4.2)

Для рассматриваемого состояния этот эффект зависит только от управления на шаге. Условно-оптимальное управление и условно-оптимальный эффект для состояния определяются в общем случае как экстремальное значение

(4.3)

Так определяется основное уравнение динамического программирования.

При условной оптимизации, выполняемой из состояния в качестве рассматривается состояние в конце i-го шага. В этом случае основное уравнение записывается в следующем виде

. (4.4)

Рассмотрим несколько примеров планирования операций методом динамического программирования.

Пример 1. Необходимо выбрать лучший вариант размещения капитала 5 000 рублей в банки для получения максимального дохода. Ожидаемая прибыль на вклады в размере К для трёх банков приведена в табл. 4.1, где все денежные средства даны в тысячах рублей.

Таблица 4.1

Решение начинаем с разделения операции на этапы. В качестве этапа принимается вложение в конкретный банк, т. е. операция искусственно разбивается на три этапа.

Состояние оценивается общим объемом вложенного капитала на этапе. Управление – объем вложений на этапе . ,Эффект на шаге – прибыль от вложения в конкретный банк.

Основное уравнение динамического программирования для задачи имеет вид

. (4.5)

При этом доход на шаге зависит только от объёма вложений в рассматриваемый банк 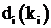. Состояние определяется условием .

Процесс условной оптимизации начнем с начального состояния. Диаграмма процесса условной оптимизации показана на рис. 4.5. На этапах 1 и 2 показаны лишь условно-оптимальные управления для каждого состояния, а на этапе 3 все возможные управления, приводящие в конечное состояние.

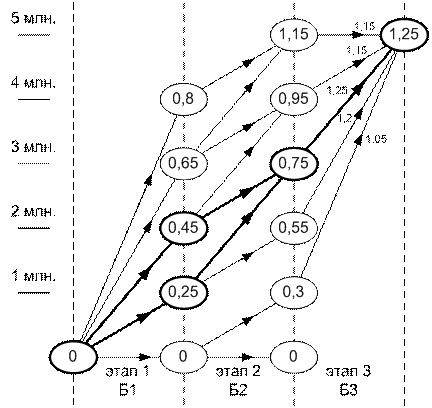
Рис. 4.5

Обратным ходом получено два равноценных варианта размещения капитала с доходом в 1250 рублей.

Первый вариант: 2000 рублей размещают в первый банк, 1000 рублей во второй и 2000 рублей – в третий.

Второй вариант: 2000 рублей размещают в первый банк, 2000 рублей во второй, 1000 рублей – в третий.

Пример 2. Имеется 3 площадки, где могут сооружаться КЭС с разным количеством блоков по 100 МВт. Капитальные затраты в относительных единицах на вводимую мощность для каждой электростанции представлены в табл. 4.2.

Дефицит мощности в системе 400 МВт.

Таблица 4.2

Необходимо определить установленную мощность электростанций по минимуму затрат.

В качестве этапов будем рассматривать ввод отдельных электростанций: на первом – ЭС-1, на втором – ЭС-2, на третьем – ЭС-3.

Состояние системы будем определять по установленной мощности всех КЭС в конце каждого этапа . Исходное состояние – , конечное состояние – . Шаг для изменения состояния принят равным мощности блока, т. е. 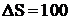. Управление на каждом этапе – объем вводимой мощности на соответствующей электростанции. Будем рассматривать такие управления , которые могут принимать значения 0, 100, 200 или 300 МВт.

В качестве эффективности на шаге примем капитальные вложения в i-ю электростанцию. Эффективность операции определяется общими капитальными вложениями на всех рассмотренных этапах.

Основное уравнение динамического программирования для рассматриваемой операции

. (4.6)

Функциональные зависимости, определяющие состояние и управление, .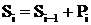

Диаграмма процесса условной оптимизации, проводимой от начала, показана на рис. 4.6.

Обратным ходом определена оптимальная траектория развития операции.

По оптимальной схеме на КЭС-2 вводится 100 МВт и на КЭС-3 вводится 300 МВт, с общими капитальными вложениями К = 36 о. е.

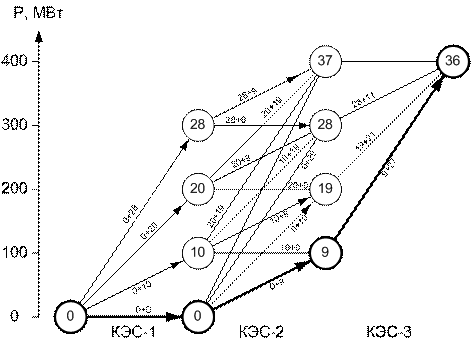
Рис. 4.6

Пример 3. Выбор оптимального графика сработки водохранилища на ГЭС.

Рассматривается ГЭС с суточным циклом регулирования, которая работает в энергосистеме параллельно с тепловыми электростанциями. Располагаемый ресурс воды на сутки определяется прогнозируемой приточностью. Режим ГЭС определяется графиком использования воды, который контролируется по уровню зеркала водохранилища, называемого горизонтом верхнего бьефа (ГВБ).

Задача заключается в выборе такого графика, при котором обеспечивается минимальный расход топлива на тепловых станциях.

В этой задаче этапы определяются ступенями суточного графика нагрузки. Состояние оценивается отметкой ГВБ, которую обозначим через . Управление – изменение отметки ГВБ на шаге. Эффект на шаге определяется расходом топлива на тепловых станциях . Условно оптимальная эффективность – оптимальный расход топлива на всех рассмотренных шагах при условии, что отметки ГВБ находятся на уровне .

Основное уравнения динамического программирования здесь имеет вид:

. (4.7)

В этой задаче рассмотрим лишь функциональные зависимости, определяющие связь состояния, управления и расход топлива на шаге.

Зависимость состояний от управления проста и определяется условием .

Определение расхода топлива требует специальных расчётов, в которых используется следующая информация:

–  отметки ГВБ в начале и конце рассматриваемого шага продолжительностью час;

–  зависимость объёма водохранилища от отметки ГВБ, определяемая профилем зоны затопления;

–  прогнозируемый график нагрузки системы ;

–  прогноз приточности ;

–  расходная характеристика ТЭС , определяющая часовой расход топлива в зависимости от мощности;

–  зависимость горизонта нижнего бьефа от расхода воды .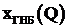

Алгоритм расчёта расхода топлива на ТЭС приводится ниже.

1.  Для отметок и ГВБ определяются объёмы водохранилища и .

2.  Определяется изменение объёма .

3.  Рассчитывается средний расход воды в м3/с на ГЭС .

4.  Определяется отметка ГНБ по функции .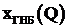

5.  Рассчитывается средний напор на шаге .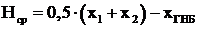

6.  Определяется мощность ГЭС .

7.  Определяется нагрузка ТЭС .

8.  Определяется расход топлива .

4.4. Методика решения задач

Рассмотренные примеры дают некоторое представление об общей идее динамического программирования. Главное здесь – пошаговая оптимизация, в результате которой для каждого состояния определяются условно-оптимальные эффективности и управления, и обратный ход, определяющий оптимальную траекторию процесса.

И ещё один вывод – для метода не существует единой вычислительной процедуры. В каждой задаче используются разные функциональные зависимости, связывающие состояние, управление и эффективность. В рассмотренных примерах это были таблицы, простые формулы и громоздкие алгоритмы.

Определим некоторые общие вопросы, связанные с постановкой и решением оптимизационных задач методом динамического программирования.

1.  Как разбить операцию на этапы? Этапы могут определяться естественным путём, когда процесс развивается во времени. В качестве этапа могут рассматриваться отдельные объекты, по которым принимаются решения (банки, электростанции и т. д.). Принципиальным является вопрос о выборе числа шагов, на которые разбивается расчётный временной период. При увеличении его растёт объем вычислений, при уменьшении – теряется точность. При выборе необходим разумный подход, определяемый требованиями практики.

2.  Выбор параметров, определяющих состояние системы на каждом шаге. В рассмотренных примерах состояние определялось всего лишь одним параметром: капиталом К, мощностью Р или отметкой ГВБ. В общем случае число параметров может быть значительно бóльшим, что вызывает многократное увеличение объёма вычислений. Поэтому говорят, что над динамическим программированием давлеет «проклятие размерности». На объём вычислений влияет и шаг изменения параметра, характеризующего состояние, который определяется принятым управлением.

3.  Выбор параметров, через которые можно управлять процессом. Их может быть несколько, объединённых в вектор управления U. Для каждого параметра необходимо определить величину шага и диапазон изменения.

4.  Определение функциональной зависимости для расчёта эффекта на шаге для различных состояний и управлений

.

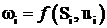5.  Определение функциональной зависимости для состояния в конце шага

.

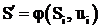6.  Запись основного уравнения динамического программирования, которое определяет условный оптимальный эффект 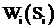через ранее найденные или в зависимости от направления условной оптимизации.

7.  Проведение условной оптимизации первого или последнего шага и определение условной эффективности для каждого рассматриваемого состояния.

8.  Проведение условной оптимизации для всех последующих шагов. При этом для каждого состояния в начале шага, если процесс идёт с конца, или в конце шага, если процесс идёт с начала, рассматриваются все возможные управления, и по основному уравнению определяется условное оптимальное управление. Здесь реализуется «принцип оптимальности»: для любого состояния системы перед очередным шагом управление на шаге выбирается так, чтобы общий эффект на данном шаге в сумме с оптимальным эффектом на всех последующих шагах был максимальным. Это управление и соответствующая эффективность запоминаются для использования в процессе «обратного хода».

9.  Проведение безусловной оптимизации обратным ходом, в результате которой определяется оптимальная траектория развития процесса.

В заключение одно замечание. Все рассмотренные задачи как, впрочем, и большинство практических задач, характеризуются аддитивным критерием

.

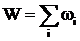Однако алгоритм динамического программирования будет работать, и при мультипликативном критерии, когда

. (4.9)

Примером такого критерия является вероятность рабочего состояния в задаче повышения надежности работы системы, состоящей из нескольких последовательных блоков, путём рационального вложения выделенных средств в отдельные блоки (рис. 4.7).

Рис. 4.7

Если обозначить вероятности надежной работы блоков соответственно 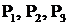, то вероятность надежной работы системы определяется произведением .

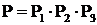Математически задача заключается в поиске максимально высокой надёжности работы системы при ограничении средств

где – вероятность надёжной работы i-го блока, зависящая от капитальных вложений, – выделяемые вложения.

Глава 5. Марковские случайные процессы

5.1. Понятие о марковском процессе

В предыдущих главах были рассмотрены детерминированные задачи исследования операций и методы поиска оптимальных решений в этих условиях.

Эта глава будет посвящена поиску решений в условиях неопределенности, причиной которой являются случайные события или случайные величины. При этом считается, что их вероятностные характеристики известны или могут быть получены на основе опыта и статистических данных. В этих задачах даже составление математических моделей затруднено. Однако, в особых случаях, когда исследуемая операция представляет собой хотя бы приближенно марковский случайный процесс, математическая модель может быть сформулирована.

В мире, нас окружающем, все процессы в той или иной мере носят случайный характер, и пока случайные возмущения мало влияют на интересующие нас параметры, мы рассматриваем процесс как детерминированный. Необходимость учета случайного характера возникает не часто. Например, при анализе работоспособности электрической сети можно необходимую нагрузку в узлах принимать как детерминированную. Но когда надо оценивать отпущенную потребителю электроэнергию для денежных расчетов или контролировать качество напряжения требуется учет случайного характера процессов электроснабжения.

Случайный процесс, протекающий в системе, называется марковским, если для любого момента времени t0 вероятностные характеристики процесса в будущем зависят только от состояния в данный момент и не зависят от того, когда и как система пришла в это состояние [1,2]

Пусть в настоящий момент t0 (рис 5.1) система находится в состоянии S0. Известна предыстория процесса (t < t0), но главный интерес заключается в предсказании будущего (t > t0). Точное предвидение в условиях действия случайностей невозможно, но оценка некоторых вероятностных показателей процесса в будущем вполне реальна, например, определение вероятности того, что система за расчетное время τ перейдет в другое состояние S1 и т. п.

Рис. 5.1

Для марковского процесса прогноз возможен на основе учета только текущего состояния S0 без учета поведения системы при t < t0.

Примером марковского процесса может служить измерительная система учета электроэнергии, включающая измерительные трансформаторы тока и напряжения и счетчик электроэнергии. Пусть в момент t0 счетчик показывает W0 кВт·ч. Вероятность того, что в момент t > t0 счетчик зафиксирует какое-либо новое значение W1 зависит от W0, но не зависит от того, как ранее во времени менялась нагрузка потребителя.

На практике обычно встречаются процессы, которые лишь приближенно могут рассматриваться как марковские. Например, состояние рабочей мощности всех электростанций системы в момент t0 характеризуется величиной P0 МВт. Вероятность сохранения такой мощности к моменту t0 + τ зависит в основном от состава блоков в момент t0, и не зависит от того, когда накануне и насколько аварийно отключались блоки и выводились в ремонт. Если в этой ситуации предысторию включить в настоящее состояние системы путем корректировки некоторых вероятностных показателей, характеризующих надежность оборудования и его остаточный ресурс, то процесс можно уже с бóльшим основанием рассматривать как марковский.

В технике интерес представляют марковские случайные процессы с дискретным состоянием и непрерывным временем. В таких процессах число состояний Si ограничено и заранее известно и переход из одного состояния в другое может произойти «скачком» практически мгновенно и в любой случайный момент времени.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8