Участвуют два игрока, которые по команде «выбрасывают» 1, 2 или 3 пальца. Исход равен сумме «выброшенных» пальцев, если она четная – выигрывает А, нечетная – В. Имеем игру 3×3 с платежной матрицей, приведенной в табл. 7.2.
Таблица 7.2.
Вj Ai | В1 | В2 | В3 |
А1 | 2 | -3 | 4 |
А2 | -3 | 4 | -5 |
А3 | 4 | -5 | 6 |
3. Договор на поставку топлива на зимний период
В порядке подготовки к зиме энергетик предприятия должен подготовить договор на поставку топлива. Известно, что потребности в топливе зависят от характера зимы. При теплой достаточно 100 т, средней – 140 т, суровой – 180 т. Поставщик определяет цену за Т топлива – плановую 300 руб, при теплой зиме – 350, средней – 400, суровой – 450.
Участвуют два игрока – мы (игрок А) и природа (игрок В). У нас рассмотрим три стратегии: А1 заказ 100 т в расчете на теплую зиму, А2 – заказ 140 т, и А3 – заказ 180 т. У природы также три стратегии: В1 – теплая, В2 – средняя, В3 – суровая.
Составим платежную матрицу (табл. 7.3).
Таблица 7.3.
| Расчет элементов матрицы в тыс. руб. a11 = 100×0,3 = 30 a21 = 140×0,3 = 42 a31 = 180×0,3 = 54 = а32 = а33 a12 = 30 + 40×0,4 = 46 a13 = 30 + 80×0,45 а22 = 42 а23 = 42 + 40×0,45 = 60 |
7.2. Основные критерии теории игр
Рассмотрим игру 3×4 с матрицей игры, приведенной в табл. 7.4. В этой игре у нас на выбор три стратегии, а у игрока В – 4.
Проведем анализ своих возможностей и видов на максимальный выигрыш.
Таблица 7.4 | ||||||
Вj Ai | В1 | В2 | В3 | В4 |
| |
A1 | 8 | 4 | 9 | 7 | 4 | |
A2 | 6 | 12 | 4 | 2 | 2 | |
A3 | 9 | 7 | 6 | 8 |
| |
| 9 | 12 | 9 |
|
Наибольший выигрыш, равный 12, нам может дать стратегия А2, но здравомыслящий противник в ответ может выбрать стратегию В4 и мы получим всего 2. И это вместо 12!
Очевидно, следует более осторожно выбирать свою стратегию, например так, чтобы наш минимальный выигрыш был максимальным. В этом суть принципа минимакса: поступай так, чтобы при наихудшем для тебя поведении противника получить максимальный выигрыш [1, 2].
В столбик αi запишем ![]() . Наибольшее значение
. Наибольшее значение ![]() называют нижней ценой игры
называют нижней ценой игры
![]() , (7.1)
, (7.1)
которая и определяет оптимальную минимаксную стратегию.
Выбор этой стратегии гарантирует нам выигрыш не меньше нижней цены игры.
Поставим теперь себя на место противника – игрока В. Анализируя свои стратегии, например, В1, он оценит свой результат при нашем лучшем ходе А3, который сулит ему проигрыш 9.
Запишем в строчку ![]() – наихудшие результаты для игрока В.
– наихудшие результаты для игрока В.
![]() .
.
Очевидно, наилучшая стратегия игрока В должна выбираться по принципу минимакса
![]() . (7.2)
. (7.2)
Приняв стратегию В4 игрок В больше чем 8 не проиграет. Полученное значение ![]() называют верхней ценой игры.
называют верхней ценой игры.
Таким образом, перестраховавшись в расчете на худшее, мы должны принять стратегию А3, противник В4. Выигрыш будет равен а34 = 8.
Однако, игрок В, узнав, что мы принимаем стратегию А3, выберет стратегию В3, и наш выигрыш уменьшится до 6. Но и мы в ответ примем А1 и увеличим выигрыш до 9 и т. д. Получается, что минимаксные стратегии в нашем случае неустойчивы.
Существуют ситуации, когда ![]() . В это случае минимаксные стратегии игроков А и В будут устойчивыми. Пример такой игры приведен в табл. 7.5. В этом случае
. В это случае минимаксные стратегии игроков А и В будут устойчивыми. Пример такой игры приведен в табл. 7.5. В этом случае 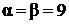 и игрокам нет смысла менять свои минимаксные стратегии А2 и В3.
и игрокам нет смысла менять свои минимаксные стратегии А2 и В3.
Таблица 7.5 | ||||||
Вj Ai | В1 | В2 | В3 | В4 |
| |
A1 | 5 | 8 | 6 | 4 | 4 | |
A2 | 12 | 10 | 9 | 11 |
| |
A3 | 6 | 7 | 5 | 10 | 5 | |
| 12 | 10 |
| 10 |
Такие игры называют играми с седловой точкой.
Ценой игры v называют значение ![]() , то есть,
, то есть, ![]() .
.
Про такую игру говорят, что она решается в чистых стратегиях. Наличие седловой точки в игре встречается нечасто.
Особое место среди игр без седловой точки занимают игры с природой, в которых наш противник – природа далеко не злонамерена по отношению к нам, но и непредсказуема.
На первый взгляд может показаться, что поиск решений в этой ситуации проще. Однако в игре с реальным думающим противником часть неопределенности в его действиях снимается в расчете на его здравый смысл.
Поэтому теория принятия решений в играх с природой не может давать однозначных рекомендаций и поэтому базируется на основе нескольких критериев.
Вернемся к уже ранее рассматриваемой игре с природой 3×3, для которой мы составляли платежную матрицу (табл. 7.6).
Таблица 7.6
| Напомним стратегии природы – характер зимы: В1 – теплая, В2 – средняя, В3 – суровая. Наши стратегии: А1 – заказ 100 т, А2 – заказ 140 т, А3 – заказ 180 т топлива на зиму. |
Рассмотрим возможные критерии для выбора наилучшей стратегии.
1. Максимальный критерий Вальда
Это критерий, используемый в играх со злонамеренным противником. Поскольку в нашей игре рассматриваются затраты, а не выигрыш, то критерий записывается так:
![]() . (7.3)
. (7.3)
По этому критерию оптимальная стратегия А3, выбранная с ориентацией на самую плохую ситуацию, в расчете на невезение. Такой критерий можно оценить как крайне пессимистический, который в играх с природой вряд ли оправдан.
2. Миниминный критерий
Это критерий крайнего оптимизма, рассчитанный на везение и счастливый случай
![]() . (7.4)
. (7.4)
Соответствующая ему стратегия А1. Опасный критерий.
3. Критерий Гурвица
В соответствии с этим критерием наилучшая стратегия выбирается как компромиссная между крайним пессимизмом и крайним легкомыслием
![]() , (7.5)
, (7.5)
где ![]() – коэффициент, выбираемый экспертным путем.
– коэффициент, выбираемый экспертным путем.
При ![]() и
и ![]() получаем крайние критерии, а при
получаем крайние критерии, а при ![]() получается промежуточная стратегия. Например, при
получается промежуточная стратегия. Например, при 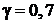 получим
получим
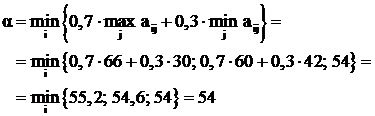
Лучшей по Гурвицу при ![]() является стратегия А3.
является стратегия А3.
4. Критерий недостаточного обоснования
По этому критерию все стратегии природы принимаются равновероятными.
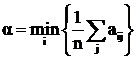 , (7.6)
, (7.6)
где n – количество стратегий природы.
В нашем случае ![]() и лучшей является стратегия А1.
и лучшей является стратегия А1.
5. Критерий минимального риска Сэвиджа
Здесь анализируется специально составленная по исходной платежной матрице матрица риска R. Любой элемент ее определяется по выражению
![]() (7.7)
(7.7)
Матрица риска (табл. 7.7 ) анализируется по минимаксному принципу
Таблица 7.7
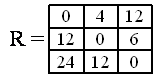
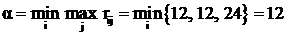 .
.
По этому критерию наилучшие стратегии А1 и А2.
Конечно, выбор решения в условиях неопределенности во многом субъективен, что и определяет неоднозначность решений. Но и здесь применение математики не бесполезно. Если стратегии, рекомендуемые по нескольким критериям совпадают, то их и можно рекомендовать к реализации. В рассмотренном примере эта стратегия А1, она скорее всего «не подведет». Можно вспомнить прошедшие зимы.
Ну а если явных фаворитов среди стратегий нет, то надо насколько можно уточнить ситуацию и самим сделать окончательный выбор.
7.3. Решение игр в смешанных стратегиях
Как уже было отмечено, наряду с чистыми стратегиями, определяемыми в соответствии с рассмотренными критериями, в отдельных ситуациях, когда игра повторяется много раз, могут применяться смешанные стратегии, в которых ходы игроков выбираются случайным образом с помощью жребия.
Используя смешанные стратегии игрок полностью полагается на волю случая, скрывая тем самым свою тактику, которой может и не быть, от противника. Такие стратегии целесообразны в играх, подобных ранее рассмотренным («орел-решка», «три пальца»), при планировании военных операций, не исключено, что и при решении каких-либо вопросов управления в технико-экономических системах, хотя в литературе подобные примеры не встречались.
Предлагаемый параграф можно рассмотреть для более полного представления о теории игр.
Итак, смешанные стратегии игроков А и В определяются вероятностями применения каждой стратегии из числа возможных. Например, для игры (m×n)
![]() (7.8)
(7.8)
где 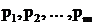 – вероятности применения игроком А стратегий
– вероятности применения игроком А стратегий ![]() ;
;
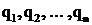 – вероятности применения игроком В стратегии
– вероятности применения игроком В стратегии ![]() .
.
Естественно, 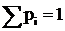 ,
, 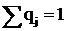 .
.
Для теории игр справедлива следующая основная теорема: любая конечная игра двух лиц с нулевой суммой имеет по крайней мере одно решение – пару оптимальных смешанных стратегий (![]() ,
,![]() ) и соответствующую цену
) и соответствующую цену ![]() .
.
Стратегии, для которых ![]() ,
, ![]() называют активными. Для решения игр важное значение имеет теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры
называют активными. Для решения игр важное значение имеет теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры ![]() , независимо от того, что делает другой игрок, если он не выходит за пределы своих активных стратегий, смешивая их в любых пропорциях.
, независимо от того, что делает другой игрок, если он не выходит за пределы своих активных стратегий, смешивая их в любых пропорциях.
Рассмотрим самую простую конечную игру 2×2 с матрицей (рис. 7.1).

Рис. 7.1
По теореме об активных стратегиях математическое ожидание выигрыша, если противник принимает первую стратегию,
![]() ,
,
и если он выбирает вторую стратегию,
![]() .
.
Из этих двух уравнений, учитывая условие
![]()
найдем решение:
![]()
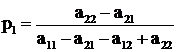 (7.9)
(7.9)
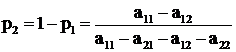 . (7.10)
. (7.10)
Цена игры:
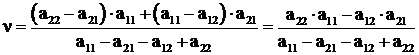 . (7.11)
. (7.11)
Аналогично можно найти выражения для q1 и q2
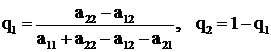 .
.
Проверим решение для игры «орел-решка» с матрицей, показанной на рис. 7.2.
Вj Ai | В1 | В2 |
А1 | –1 | 1 |
А2 | 1 | –1 |
Рис. 7.2
По формулам (7.9), (7.10), (7.11) получаем
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() .
.
Значит, оптимальная стратегия каждого игрока состоит в том, чтобы случайным образом чередовать свои чистые стратегии с вероятностью 0,5. При этом средний выигрыш будет равен нулю.
7.4. Решение игр n×m.
Рассмотрим игру n×m с матрицей (рис 7.3):
Оказывается, решение таких игр сводится к задаче линейного программирования. Найдем оптимальную смешанную стратегию ![]() .
.
В1 | … | Вm | |
|
|
|
|
Рис. 7.3
По теореме об активных стратегиях она должна обеспечить нам выигрыш не меньший ![]() при любом поведении противника и равный
при любом поведении противника и равный ![]() при его оптимальной стратегии
при его оптимальной стратегии ![]() .
.
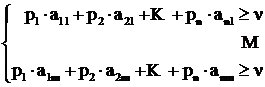 (7.12)
(7.12)
В системе (7.12) поделим все неравенства на положительную величину ![]() и введем следующие обозначения:
и введем следующие обозначения:
![]()
Тогда условия (7.12) можно записать в виде
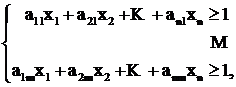 (7.13)
(7.13)
где 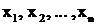 – неотрицательные переменные, которые в силу
– неотрицательные переменные, которые в силу ![]() удовлетворяют условию
удовлетворяют условию
![]() (7.14)
(7.14)
Стремление обеспечить наибольший выигрыш приводит к необходимости минимизации функции 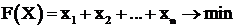 с учетом ограничений (7.13). Таким образом, исходная задача сводится к типичной задаче линейного программирования, решение которой позволяет найти оптимальную стратегию
с учетом ограничений (7.13). Таким образом, исходная задача сводится к типичной задаче линейного программирования, решение которой позволяет найти оптимальную стратегию ![]() игрока А.
игрока А.
В связи с требованием неотрицательности переменных все элементы платежной матрицы должны быть положительными. Если в ней есть отрицательные элементы, то переход к такой матрице осуществляется добавлением к элементам исходной матрицы положительного числа, равного модулю наименьшего отрицательного элемента исходной матрицы.
Аналогично можно найти оптимальную стратегию ![]() игрока В, с той лишь разницей, что В стремится минимизировать наш выигрыш
игрока В, с той лишь разницей, что В стремится минимизировать наш выигрыш ![]()
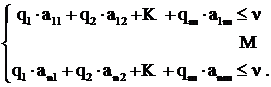 (7.15)
(7.15)
После ввода обозначений ![]() и учета условия
и учета условия ![]() получим следующую задачу линейного программирования:
получим следующую задачу линейного программирования:
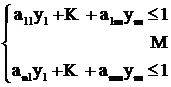
![]()
Пример. Найти решение игры «три пальца»
Матрица игры приведена на рис. 7.4, а.
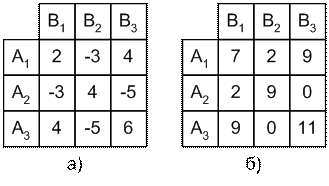
Рис 7.4
Прибавляя ко всем элементам матрицы одно и то же число ![]() сделаем их неотрицательными (рис. 7.4, б). При этом цена игры возрастет на 5, а решение не изменится. Обозначим новую цену игры
сделаем их неотрицательными (рис. 7.4, б). При этом цена игры возрастет на 5, а решение не изменится. Обозначим новую цену игры ![]() .
.
Найдем оптимальную смешанную стратегию ![]() игрока А. Система ограничений и целевая функция примет вид:
игрока А. Система ограничений и целевая функция примет вид:
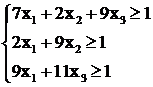
![]() .
.
Решение задачи симплекс-методом дает следующие результаты:
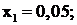
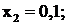
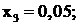
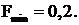
Отсюда 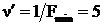 ,
, 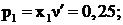
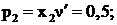
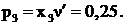
Цена игры 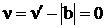 .
.
ОСНОВНАЯ ЛИТЕРАТУРА
1. Вентцель операций. – М.: Советское радио, 1972.
2. Вентцель операций. Задачи, принципы, методология. Учеб. пособие для студ. вузов. – М.: Высш. шк., 2001.
3. и др. Математическое программирование. Учеб. пособие для вузов. – М.: Высш. шк., 1976.
4. Прикладное нелинейное программирование. – М.: Изд-во МИР, 1975.
5. , Загоруйко операций. Учеб. для вузов / Под ред. , . – М.: Изд-во МГТУ им. , 2000.
6. Курпицкий решенеие? – Это очень важно! – Л.: Машиностроение, 1984.
7. Первозванский . – М.: Изд-во Наука, 1970.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |



