Исследование операций (стр. 5 )

Мы рассмотрели методы, связанные с вычислением производных, которые в зависимости от порядка производных относят к методам первого или второго порядка. Эти методы отличаются малым числом итераций, но большим объёмом вычислений на каждом приближении.

Существуют методы нулевого порядка, не требующие вычисления производных, основанные только на вычислении целевой функции. Особенность этих методов – большое число итераций при малом объёме вычислений на каждой.

При высоком быстродействии современных ЭВМ большое число итераций становится некритичным, а простые расчёты на шаге позволяют создавать более универсальные алгоритмы, способные решать более широкий круг задач нелинейного программирования.

Поэтому далее рассмотрим два метода нулевого порядка: метод случайного поиска и метод деформированного многогранника.

3.2.5.1. Метод случайного поиска

В этом методе возможное направление перехода из исходной точки , в которой вычислено значение целевой функции , определяется случайным образом.

Для этого вокруг точки рассматривается n-мерный куб (при – квадрат) с ребром δ (рис. 3.15).

Координаты новой точки определяются с помощью генератора псевдослучайных чисел 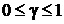с равномерным распределением.

Для осуществляется генерация двух случайных чисел, равных, например, 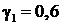и .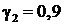

Координаты случайной точки определяются по выражениям

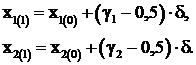(3.25)

В полученной точке считается функция и сравнивается с . Если , то переносится в , вокруг нее вновь рассматривается куб с ребром δ, выбирается случайное направление и т. д.

В случае, когда (см. рис. 3.15), делается реверс неудачного направления при тех же и

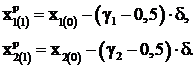(3.26)

В этом случае в новой точке значение вероятнее всего будет меньше , куда и переместится текущая точка.

При небольшом размере куба и значительном удалении от точки минимума вероятность случайного выбора возможного направления составляет 0,5.

По мере приближения к решению ребро куба уменьшается обычно в 2 раза. Основанием для этого является результат реверса направления, при котором окажется .

Траектория спуска к оптимуму носит явно выраженный случайный характер и напоминает Броуновское движение.

Достоинство метода: простые вычисления на шаге и несложная логика в организации поиска траектории спуска к решению.

Недостатки: большое число итераций и сложная траектория.

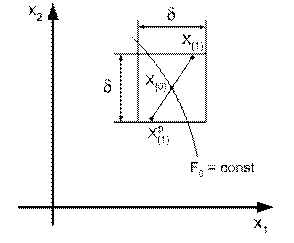
Рис. 3.15

3.2.5.2. Метод деформируемого многогранника

В этом методе вокруг исходной точки намечаются равноудаленные точки, обозначенные на рис. 3.16 номерами 1, 2, 3. В каждой точке считается целевая функция и определяются вершины с максимальным значением функции и с минимальным значением .

Затем производится деформация исходного многогранника (при треугольника) и вершина переносится через центр тяжести других вершин в точку с некоторым коэффициентом α:

. (3.27)

Рис. 3.16

Координаты определяются по формуле

. (3.28)

При деформацию называют отражением. В полученной точке считается целевая функция . Если , то α увеличивают обычно до значения и деформацию называют растяжением. При α уменьшают обычно до , что приводит к сжатию многогранника.

После этих операций вершина h переносится в точку и новый многогранник подвергается деформации по тому же алгоритму.

По мере приближения к оптимуму появляется необходимость уменьшать размер многогранника, сжимая его в 2 раза относительно вершины, в которой отмечено минимальное значение функции.

3.3. Методы учёта ограничений в форме равенств

Рассмотрим более сложную задачу нелинейного программирования, в которой обеспечивается поиск на допустимой области, определяемой системой ограничений в форме равенств . Здесь вектор-функция ограничений состоит из m функций .

Задача оптимизации имеет смысл, когда число уравнений m меньше числа неизвестных n. В этом случае существует множество решений, среди которых нужно найти решение, соответствующее минимуму функции.

Если m=n, то система ограничений может иметь единственное решение или быть несовместной, когда оптимизация теряет смысл.

Рассмотрим некоторые методы условной оптимизации.

3.3.1. Метод прямой оптимизации

Метод применяется, когда 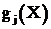описываются простыми, желательно линейными функциями, что позволяет выразить аналитически какие-либо m переменных из общего числа неизвестных, объединив их в новый вектор Y, через оставшиеся , которые называют свободными или независимыми . Найденные выражения подставим в , что позволит после преобразований получить новую по виду функцию , для которой необходимо найти минимум.

Решение полученной задачи безусловной оптимизации любым из рассмотренных методов позволит найти k неизвестных, а после подстановки их в аналитические выражения определить и остальные неизвестные.

3.2.2. Метод приведенного градиента

Метод используется в том случае, если объективно существующие зависимости , определяемые системой ограничений не удается выразить в явном виде.

В математике известно правило определения производных с учетом неявновыраженных функций.

Запишем исходную задачу с учётом разделения исходного вектора неизвестных на составляющие Y и :

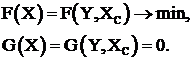(3.29)

Запишем производную с учетом неявной зависимости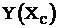

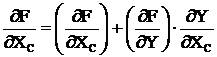, (3.30)

где производные в скобках определяются с учетом явной зависимости F от XC и Y.

Производную найдем из ограничения , которое в результате дифференцирования определяет условие

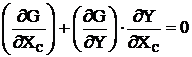, (3.31)

позволяющее получить

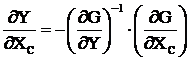. (3.32)

Здесь – квадратная матрица (), для которой существует обратная.

После подстановки (3.32) в (3.30) получим

.

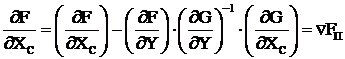Полученный градиент, составляющие которого определяются независимыми переменными, и называется приведённым градиентом.

Этот градиент может использоваться в процедуре градиентного метода:

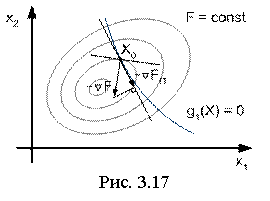
. (3.34)

Геометрически приведённый градиент является проекцией градиента на поверхность ограничений, а точнее – на плоскость, касательную нелинейной поверхности в текущей точке (рис. 3.17).

В точке условного минимума функции .

3.3.3. Метод неопределенных множителей Лагранжа

В точке, являющейся решением задач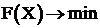и при 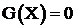, приведённый градиент равен 0, т. е.

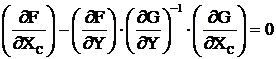. (3.35)

Введём следующее обозначение, определяющее вектор λ так называемых неопределенных множителей Лагранжа,

.

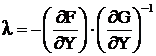С учётом λ перепишем условие (3.35) в виде системы из двух условий

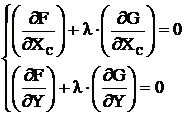, (3.36)

которые должны выполняться в точке, являющейся решением задачи.

Эту систему можно составить формально на основе условия минимума некоторой функции Лагранжа, определённой следующим образом.

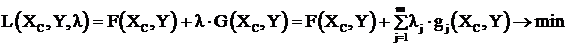. (3.37)

Действительно, условие минимума функции Лагранжа

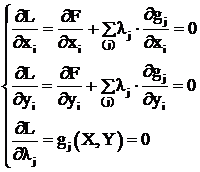. (3.38)

Полученная система из 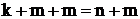уравнений позволяет найти все n неизвестных исходного вектора Х и m множителей Лагранжа.

Оказывается, функцию Лагранжа можно составить и без разделения исходного вектора Х на составляющие:

. (3.39)

Условие минимума этой функции определяется следующей системой:

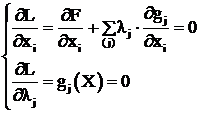(3.40)

Величина множителей Лагранжа λj может иметь практический интерес, если ограничения представляются в форме . В этом случае множители Лагранжа можно рассматривать как производные 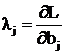, что позволяет оценивать по найденному в ходе решения (3.40) их значению возможность уменьшения целевой функции за счет изменения bj.

Ниже приводится пример решения задачи условной оптимизации рассмотренными методами.

3.3.4. Пример решения задачи нелинейного программирования

Рассмотрим пример решения следующей задачи

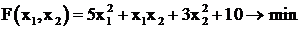
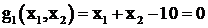
1.  Метод прямой оптимизации

В качестве независимой примем x = x1. Тогда зависимой будет x2=10–x1.

Подставим выражение для x2 в целевую функцию

.

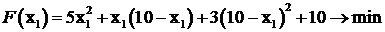Условие минимума ее:

.

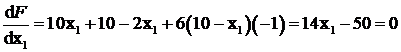Откуда 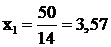и , .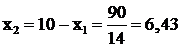

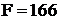2.  Метод приведенного градиента при t=0,1

Воспользуемся формулой (3.33) для приведенного градиента

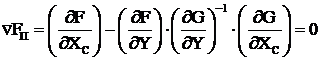
В решаемой задаче х1 является составляющей , а х2 относится к Y. С учетом этого

; ; ; .

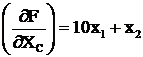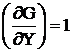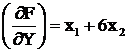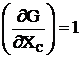С учетом этого приведенный градиент

.

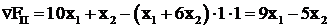В качестве исходного приближения примем

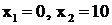
Основное уравнение градиентного метода

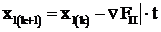
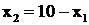
Результаты расчёта сведены в табл. 3.1, а ход итерационного процесса показан на рис. 3.18.

Видно, что процесс сходится, так как стремится к нулю.

Таблица 3.1

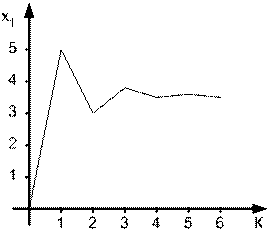
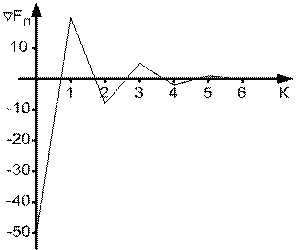
Рис. 3.18

3.  Метод множителей Лагранжа.

Составим функцию Лагранжа

Условие минимума её определяется следующей системой

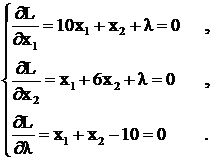
Решим полученную систему уравнений, выразив λ из первых двух уравнений и приравняв их получим

,

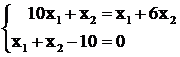откуда нетрудно найти решение, в котором , и .

Найденное значение определяет величину производной , которая позволяет оценить изменение функции L, а также и F при изменении b. Например, при целевая функция возрастет на .

3.4 Учет ограничений в форме неравенств

Наибольшие трудности в нелинейном программировании связаны с учётом ограничений в форме неравенств, например вида .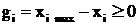

Ограничения такого типа могут накладываться не только на независимые переменные , но и на зависимые, что определяется общим условием .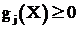

Наиболее простой подход, основанный на поиске решения без учета ограничений, последующей проверке их выполнения и закреплении переменных, нарушивших границу, на предельном значении, часто не дает правильных результатов. Примером может служить ситуация, показанная на рис. 3.19.

Здесь поиск решения без учета ограничений приведет в точку .

Проверка ограничений показывает, что два из них нарушены:

, .

Закрепление переменных на предельных значениях рекомендует для решения точку В с координатами , .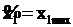

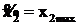При этом в допустимой области существует точка С, в которой .

Учет ограничений необходим при выборе возможного направления, которое должно вести внутрь или по границе допустимой области. На принятом направлении необходимо проверять ограничения при выборе шага. При достижении границы надо находить приведенный градиент, двигаясь по границе, не пропустить момент возможного перехода в допустимую область (схода с границы) в сторону оптимума.

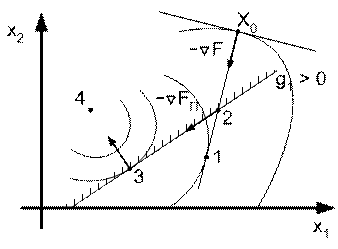
Рис. 3.20

Рассмотрим с этих позиций траекторию поиска с выбором оптимального шага, приведённую на рис. 3.20.

После выбора оптимального шага в точке Х0, который ведет в точку 1, учет ограничения должен ограничить движение в точке 2, что определяется результатом сравнения и и выбором из них минимального. Продолжая движение от точки 2 по границе необходимо двигаться в направлении до точки 3, в которой нужно сойти с границы и двигаться к оптимальной точке 4.

3.4.1 Теорема Куна-Таккера

Важное место в методологии нелинейного программирования занимает теорема и условия Куна-Таккера [4].

Рассмотрим общую задачу нелинейного программирования в форме

при .

Как известно, от неравенств можно перейти к равенствам путём введения некоторых фиктивных переменных, например вида , при которых выполняются условия

. (3.41)

Для полученной задачи можно составить функцию Лагранжа

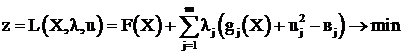. (3.42)

Условия минимума функции определяются равенством нулю всех частных производных

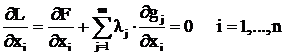(3.43)

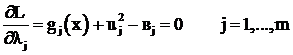(3.44)

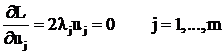
Умножив последнее условие на получим 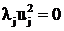или

(3.45)

Условия (3.43), (3.44) и (3.45) необходимы для существования минимума в точке при наличии ограничений.

Равенство (3.45) означает, что в этой точке должно обеспечиваться одно из двух условий: либо , либо 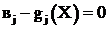. Если , то 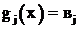и j-е ограничение является активным, т. е. выполняется в форме равенства. При этом величина определяется производной и показывает насколько снижается целевая функция при возрастании , расширяющем допустимую область.

Если же , то , т. е. минимум обеспечивается в точке, где ограничение выполняется и его можно не учитывать в функции Лагранжа.

Таким образом, необходимые условия – условия Куна-Таккера минимума при наличии ограничений , имеют такой вид, что позволяет найти Х и λ, для которых

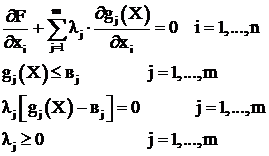. (3.46)

Рассмотрим пример, в котором требуется записать условия Куна-Таккера для следующей задачи:

при

Запишем задачу следующим образом

Функция Лагранжа

и условия Куна-Таккера

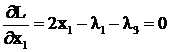
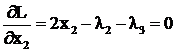
Можно проверить, что эти условия выполняются при .

При этом ограничения и являются пассивными, а – активным (рис. 3.21).

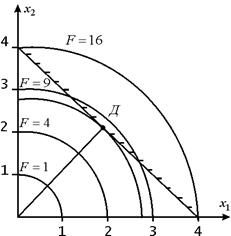
Рис. 3.21

3.4.2. Методы решения общей задачи нелинейного программирования

При решении общей задач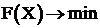и при 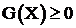могут использоваться три группы методов:

1. Методы, основанные на процедуре вычисления и анализа градиента.

Некоторые особенности и сложности реализации качественно были рассмотрены (см. рис. 3.20). Здесь направление градиента реализуется только в допустимой области. При выходе траектории на активные ограничения осуществляется переход на проекцию градиента. При движении по границе необходима проверка условия схода с границы в допустимую область. Разработано много подобных методов, наиболее полно представленных в [4].

С разработки этих методов и начиналась теория нелинейного программирования.

2. Методы, основанные на линеаризации всех нелинейностей в исходной (текущей) точке Х разложением в ряд Тейлора с учетом первых двух членов. Сформированная таким образом задача линейного программирования решается симплекс-методом. В новой точке вновь рассматриваются исходные нелинейности, проводится новая линеаризация и процесс повторяется.

3. Метод штрафных функций – наиболее простой, а в сочетании с методами нулевого порядка (случайного поиска и деформированного многогранника) позволяет получить универсальный метод, работающий для большинства практических задач.

Рассмотрим суть метода штрафных функций на примере общей задачи, в которой ограничения разделены по типам.

,

(3.47)

Метод допускает любые значения для независимых переменных xi, но при нарушении какого-либо ограничения неотвратимо и незамедлительно к целевой функции добавляется штраф, пропорциональный степени нарушения, т. е. отклонения от допустимого значения.

Комбинированная функция, куда входит исходная и все штрафные санкции составляется следующим образом:

, (3.48)

где – коэффициенты штрафа,

.

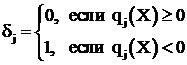Жёсткость ограничений определяется величиной . Чем больше , тем сильнее «наказание» за нарушение границы допустимой области.

Рассмотрим некоторые особенности метода на примере задачи:

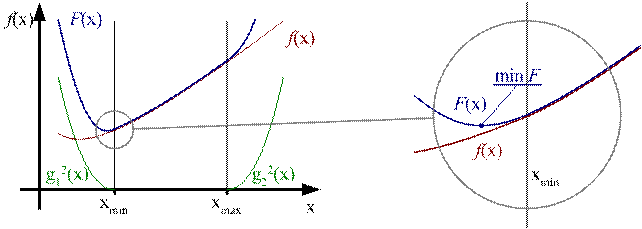
Рис. 3.22

Здесь условный минимум лежит на нижней границе (рис. 3.22).

Однако решение, найденное по минимуму штрафной функции будет лежать вблизи границы допустимой области, но за ее пределами.

Величина отклонения зависит от и в большинстве практических случаев является вполне допустимой. Стремление увеличить жёсткость ограничений может ухудшить сходимость.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8