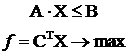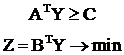Исследование операций (стр. 3 )

1. Определяется генеральный элемент по условию γj > 0, αej > 0 и при

.

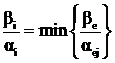Генеральный элемент подчеркивается. Определяется обратная величина

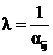
и записывается в нижнюю половинку клетки с генеральным элементом.

2. Все элементы i-й строки умножаются на и результаты записываются в нижние половинки клеток.

3. Все элементы j-го столбца умножаются на и результаты записываются в нижние половинки клеток.

4. Как-либо помечаются числа в верхних половинках клеток i-й строки и в нижних половинках клеток j-го столбца.

5. Нижние половинки остальных клеток определяются как произведение выделенных элементов строки и столбца, на пересечении которых лежит клетка.

После этого осуществляется переход к новой таблице, в которой и меняются местами. Верхние половинки клеток новой таблицы определяются по следующим правилам:

·  i-я строка и j-й столбец новой таблицы заполняются содержимым нижних половинок соответствующих клеток старой таблицы;

·  все остальные верхние половинки заполняются суммами содержимого верхних и нижних половинок соответствующих клеток старой таблицы.

Пример. Решить задачу линейного программирования

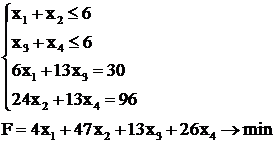(2.20)

Для перехода к канонической форме введём фиктивные переменные х5, х6 и перейдем к равенствам:

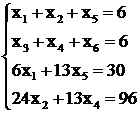
Все уравнения линейно независимы, поэтому ранг системы . Число неизвестных: , число свободных .

Рассмотрим базисное решение, в котором в качестве свободных примем и . Проверим его на допустимость при . Определим значения базисных переменных:

, , , ,

т. е. принятое базисное решение недопустимо.

Рассмотрим другой набор свободных, включающий х1 и х4.

В этом случае при 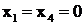все базисные переменные положительны, т. е.

, , , .

Таким образом, рассмотренное базисное решение является допустимым. Составим для него симплекс-таблицу, предварительно выразив базисные переменные и форму через свободные:

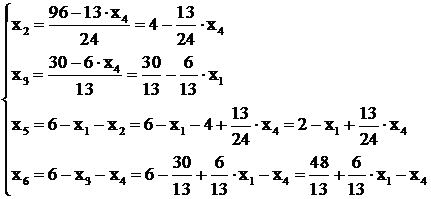(2.22)

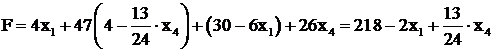
Коэффициенты заносят в таблицу в соответствии со стандартной формой записи полученных выражений, т. е. с изменением знаков. Запишем условия (2.22) в виде стандартной таблицы (табл. 2.3).

В соответствии с правилами работы с таблицей, найдем генеральный элемент. Он лежит в столбце, соответствующем свободной х1, поскольку , т. е. больше нуля. Конкурентами для перехода в свободные являются базисные и . Для них равны, соответственно, 5 и 2. По минимальному отношению выбираем , что и определяет положение разрешающего элемента . Обратная величина записывается в нижнюю часть клетки (табл. 2.4).

Теперь элементы разрешающей строки умножаются на и записываются в нижние половинки этой строки.

Элементы разрешающего столбца, умноженные на , записываются аналогично.

Таблица 2.3 Таблица 2.4

Выделение соответствующих элементов выполнено кружками.

В табл. 2.4 приведены результаты перемножения выделенных элементов.

Вторая симплекс-таблица (табл. 2.5) соответствует новому базисному решению, в котором , , , , 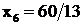и .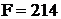

Таблица 2.5

Работаем с новой таблицей также, как с предыдущей, и составляем третью симплекс-таблицу (табл. 2.6). Она соответствует оптимальному решению, т. к. в ней все .

Таблица 2.6

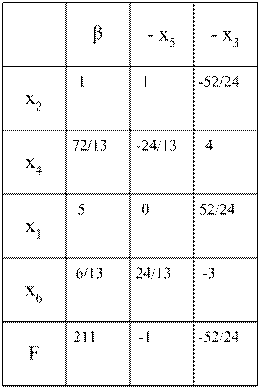
В оптимальном решени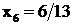и , , , и .

Поскольку в рассмотренной задаче число свободных переменных , ее можно решить графически.

Примем в качестве независимых переменных х1 и х2 и преобразуем исходную задачу к системе неравенств. Исходная система уже включает 2 неравенства:

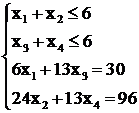(2.23)

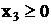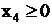Исключим x3 и x4 из уравнений системы и по условиям и получим следующие неравенства:

Преобразуем второе неравенство исходной системы:

.

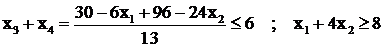Аналогично преобразуем и выражение для целевой функции

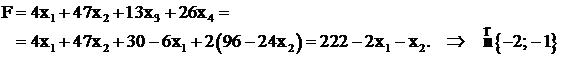
Таким образом, исходная задача описывается следующей системой

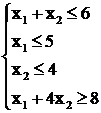, (2.24)

.

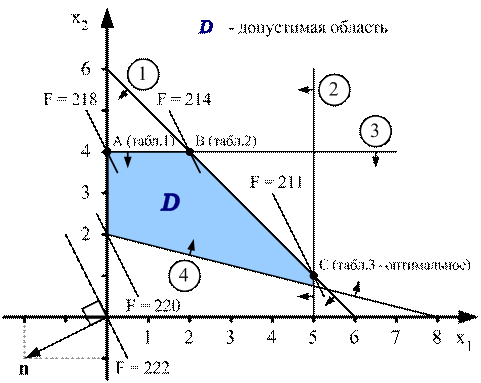
Рис. 2.5

Допустимая область D лежит в первом квадранте и формируется как пересечение полуплоскостей, являющихся решением соответствующих неравенств. Семейство параллельных линий определяется по нормали (рис. 2.5)

Решение симплекс-методом соответствует обходу вершин, начиная с вершины А, соответствующей табл. 2, по направлению снижения целевой функции.

2.8. Применение ЭВМ

Правила работы с симплекс-таблицей легко формализуются. Рассмотрим алгоритм перехода к новому базису, заключающемуся в пересчёте коэффициентов исходной таблицы. Полагаем, что в памяти ЭВМ таблица представлена двумерным массивом А (рис. 2.6), имеющем размерность .

Будем считать, что генеральный элемент уже найден и находится в строке I0 и столбце J0 массива, т. е. .

Блок-схема алгоритма показана на рис. 2.7.

Здесь введены следующие обозначения: , , .

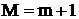В первом цикле по i организуется пересчет коэффициентов разрешающего столбца.

В следующем вложенном цикле по i, исключая разрешающую строку, и по j, исключая разрешающий столбец, идет пересчет коэффициентов всех остальных элементов таблицы.

В последнем цикле по j пересчитывается разрешающая строка.

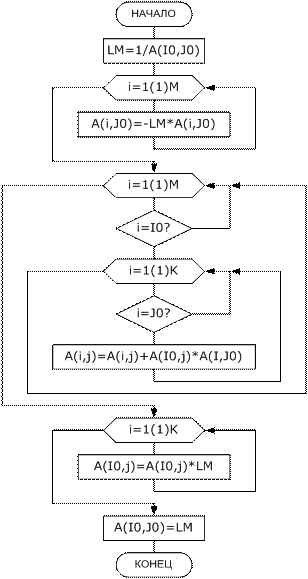
Рис. 2.7

В учебном процессе можно использовать две программы, разработанные на кафедре. Для решения линейных оптимизационных моделей может использоваться программа Simple.exe. Программа работает с любым видом ограничений, вводимых с помощью клавиш <, > и =. Переход к канонической форме условий задачи осуществляется программно.

На рис. 2.8 приведен пример решения задачи оптимального распределения топлива между энергоустановками с заданной выработкой тепла. Основные свойства системы определяются ограничениями по располагаемому топливу и условиям выработки планируемых объемов тепла. В связи с этим математическая модель включает 2 неравенства и 3 равенства

Целевая функция определяется стоимостью топлива

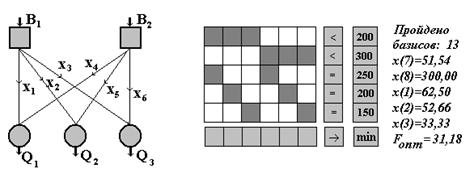
Рис. 2.8

Учитывая слабую заполненность матрицы А условий задачи, в программе предусматривается возможность ввода только ненулевых элементов. В этом случае работа начинается с расстановки ненулевых элементов в ячейках матрицы А, шаблон которой выводится на экран после ввода чисел n и m, определяющих размерность задачи. Осуществляется это перемещением с помощью стандартных клавиш навигации курсора затемненной ячейки матрицы на место ненулевого элемента с последующим нажатием Enter. Выход из режима разметки после фиксации положения всех ненулевых элементов осуществляется по Esc.

Работа с программой проводится в режиме диалога с возможностью многовариантных расчётов путём корректировки исходных данных, но без изменения размерности задачи.

По результатам решения на экран выводятся значения базисных переменных, целевой функции и количество пройденных вершин многогранника допустимых решений. На рис.2.8 показан пример решения сформулированной задачи для произвольного значения исходных данных.

Для решения задач линейного программирования могут использоваться и другие программы, реализующие алгоритм симплекс-метода. На рис.2.9 приведен пример решения транспортной задачи с помощью программы Simpl.exe. Программа практически не имеет ограничений по размерности решаемых задач. Исходная матрица условий задачи вводится своими ненулевыми элементами в таблицу, сформированную в соответствии с размерностью задачи. Навигация внутри таблицы осуществляется с помощью мышки и полос прокрутки.

Рис. 2.9

2.9. Поиск допустимого базисного решения

Реализация алгоритма симплекс-метода начинается с определения допустимого базисного решения, в котором при нулевых свободных переменных все базисные переменные положительны (не отрицательны).

Желательно, чтобы при поиске допустимого базиса по возможности более просто получались и выражения базисных переменных через свободные.

Для этой цели могут использоваться разные методы решения в зависимости от типа системы условий исходной задачи.

Если ограничения задачи линейного программирования преобразуются к виду и все bi>0, то в этом случае для перехода к равенствам в каждое неравенство вводят фиктивные переменные .

Эти фиктивные переменные и принимаются за базисные, а исходные Х за свободные. Выражения для базисных определяются исходной системой , а базисное решение является допустимым.

Целевая функция при этом не меняется .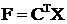

Если ограничения заданы в виде 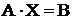и в каждом уравнении есть неизвестная , которая встречается только в этом уравнении, то в матрице условий задачи А можно выделить блок, являющийся единичной матрицей (рис. 2.10). Неизвестные, соответствующие этой матрице, можно принять в качестве базисных.

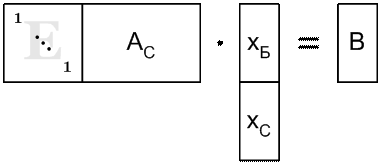
Рис. 2.10

Записав операции над блочными матрицами получим

,

откуда можно найти выражения для базисных переменных и формы

,

. (2.25)

Для выделения базисных переменных в общей задаче и представления их через свободные может использоваться метод исключения Жордана.

Для поиска допустимого базиса в этом случае может использоваться метод расширенной задачи, которая формируется путём ввода дополнительных переменных zi в каждое уравнение. Эти переменные и принимаются за базисные . В допустимом решении все должны стать равными нулю. Для того, чтобы обеспечить это условие в рамках алгоритма симплекс-метода, переменные zi вводятся в целевую функцию с большим штрафным коэффициентом:

. (2.26)

Применение симплексного метода к расширенной задаче обеспечивает поиск решения, в котором все . Если в решении хотя бы одна переменная остается большей нуля, т. е. , то исходная задача не совместна и не имеет решения.

2.10. Понятие двойственности в линейном программировании

В математике бывают ситуации, когда для некоторой задачи можно по определённым правилам построить другую, из решения которой автоматически получается решение исходной.

В линейном программировании каждая задача имеет двойственную задачу и по решению одной можно находить решение другой.

Сопоставляя математическую запись задач 1 и 2, можно отметить следующие особенности:

·  если в задаче 1 имеем m неравенств для n неизвестных, то в задаче 2 n противоположных по знаку неравенств для m неизвестных,

·  коэффициенты системы условий задачи 2 формируются путем транспонирования матрицы А задачи 1,

·  если в задаче 1 определяется максимум F, то в задаче 2 – минимум,

·  коэффициенты целевой функции одной задачи являются правыми частями ограничений другой,

·  по теореме двойственности .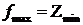

Обычно эти задачи имеют экономический смысл и могут использоваться для поиска путей повышения эффективности производства.

В качестве примера рассмотрим упрощенную задачу распределения ресурсов, которая решается при планировании производства трансформаторов на максимум прибыли.

Предположим, на предприятии производят два типа трансформаторов, которые реализуются на рынке по цене , .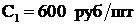

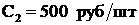При изготовлении используются три основных вида ресурсов – железо, медь и изоляция, запасы которых известны и равны соответственно , и 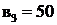кг. Определены расходы ресурсов на один трансформатор каждого типа, которые приведены в табл. 2.7.

Составим математическую модель исходной задачи.

В качестве неизвестных примем: х1 – объём выпуска Т1 и х2 – объём выпуска Т2.

Модель учитывает ограничения по ресурсам и целевую функцию:

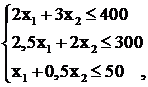(2.28)

.

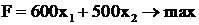Решение: x1 = x5 = 0, , x3 = 100, x4 = 50 и F = 50000 руб.

Таким образом, в оптимальном плане выгодно производить трансформаторы Т2 в количестве 100 штук. Остаток железа – 100 кг, меди – 50 кг, изоляция в дефиците и используется полностью.

Двойственная задача позволяет определить условную (теневую) цену единицы каждого ресурса, чтобы минимизировать затраты на имеющееся сырьё.

Введём переменные: y1 – стоимость железа; y2 – цена меди; y3 – цена изоляции.

Сформируем двойственную задачу с учётом отмеченных выше особенностей:

.

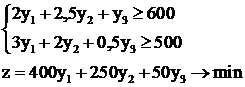Решение этой задачи:

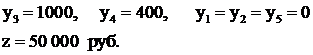
Полученные теневые цены позволяют выявить степень дефицитности каждого ресурса. При этом найденная цена определяется приращением ∆f при увеличении запаса дефицитного ресурса на единицу.

Здесь используются следующие свойства двойственности оценок yi:

·  положительная оценка yi может быть только у ресурса, который в оптимальном плане полностью исчерпан;

·  величина yi для каждого дефицитного вида ресурса показывает, насколько можно увеличить f, если ввести в производство дополнительно единицу ресурса вi.

В полученном решении теневая цена изоляции 1000 руб/кг определяется приращением прибыли, которую можно получить на каждый дополнительный кг изоляции, позволяющий получить еще 2 трансформатора по 500 руб за штуку.

Решение двойственных задач позволяет оценивать пути повышения рентабельности производства.

2.11. Целочисленное программирование

Задачи, в которых все составляющие вектора Х или часть из них могут быть только целыми, называются целочисленными. Алгоритмы их решения гораздо сложнее алгоритмов решения непрерывных задач линейного программирования.

На первый взгляд наиболее простым методом решения целочисленных задач является метод округления, по которому на первом этапе решается симплекс-методом общая задача, не учитывающая требование целочисленности переменных, а затем получившиеся базисные переменные, не являющиеся целыми, округляются до ближайших целочисленных значений.

Однако при этом полученное решение может значительно отличаться от оптимального. Поэтому для решения задач целочисленного программирования разработаны специальные более сложные методы.

Некоторые вопросы, связанные с решением таких задач, рассмотрим на примере следующей целочисленной задачи

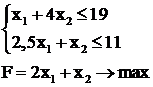. (2.29)

Графическое решение этой задачи показано на рис. 2.11.

Оптимальное решение задачи без учёта целочисленности лежит в вершине 1, координаты которой приведены в табл. 2.8., и не удовлетворяют требованиям целочисленности. Естественное округленное значение, соответствующее точке 2 оказывается недопустимым. Оптимальное решение лежит в точке 4.

На этом простом примере видно, что округление оптимальных непрерывных значений до целых может приводить к недопустимым решениям и для поиска оптимального целочисленного решения может потребоваться перебор большого числа комбинаций возможных округленных значений. Поэтому для поиска оптимального целочисленного решения разработаны специальные методы.

Рис. 2.11

Таблица 2. 8

Наиболее популярен метод отсекающих плоскостей (метод Гомори). Метод основан на поиске непрерывного решения, проверке его на целочисленность и формировании при необходимости дополнительных специальных ограничений, отсекающих найденную нецелочисленную вершину. Решение расширенной задачи подвергается аналогичной обработке.

Другой метод, называемый методом ветвей и границ, основан на направленном переборе целочисленных вершин, расположенных вблизи непрерывного решения. При этом всё множество целочисленных вершин делится на два подмножества, в каждом из которых рассматриваются округленные значения только для одной базисной хi.

Диаграмма ветвления показана на рис 2.12.

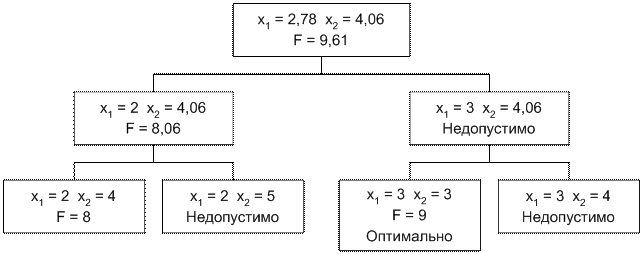
Рис. 2.12

Метод ветвей и границ даёт возможность решать задачи с любым числом целочисленных переменных.

2.12. Транспортная задача

Одной из наиболее простых и распространённых задач линейного программирования является транспортная.

Смысл задачи предельно ясен: имеется несколько поставщиков и потребителей определенного продукта. Заданы известные объемы продукта у поставщиков и потребности у потребителей. Известны также расстояния по существующим трассам от каждого потребителя до каждого поставщика. Задача заключается в определении таких направлений и объемов транспорта продукта, при которых обеспечивается минимальный грузопоток, определяющий общие транспортные расходы.

Составим математическую модель для простейшей задачи, включающей двух поставщиков с запасами D1 и D2, и двух потребителей с потребностью В1 и В2 (рис 2.13). Известны расстояния между объектами l1, …, l4.

В зависимости от соотношения объёмов продукта у поставщиков и потребителей различают закрытую задачу, когда 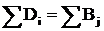, и открытую, когда .

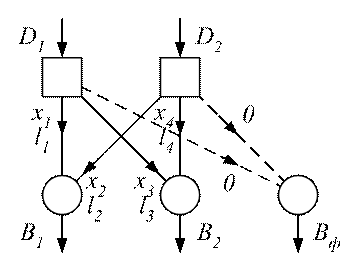
Рис. 2.13

Открытую задачу можно свести к закрытой, если ввести фиктивного потребителя с потребностью , длины путей к которому равны нулю.

Составим математическую модель.

Введем переменные: – неизвестные объемы продукта, транспортируемого по соответствующим путям.

Опишем основные свойства системы, включающие условия баланса продуктов у потребителей и поставщиков:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8