Исследование операций (стр. 2 )

F(X) =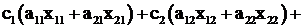

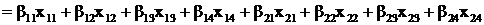. (2.5)

Требуется найти такое неотрицательное решение, которое удовлетворяет ограничениям и обеспечивает максимум F(X).

При составлении математической модели учет и описание свойств системы и ее связей производится ограничениями g(X) в виде равенств и неравенств. В задаче линейного программирования, имеющей канонический вид, ограничения представляются в форме равенств. Переход от неравенств к равенствам осуществляется путем введения фиктивных переменных.

Неравенства типа требуют ввода положительной переменной; например, неравенство 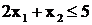преобразуется в равенство , где .

Неравенства типа требуют ввода положительной переменной, но с отрицательным знаком; например, 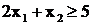преобразуется в , где .

С вводом фиктивных переменных система условий задачи принимает вид А∙Х = В, но число неизвестных при этом возрастает.

В рассмотренных примерах целевая функция имеет разные типы экстремума. В дальнейшем будут рассматриваться методы поиска минимума. Если метод решения ориентирован только на поиск минимума целевой функции, то в случае решения задачи достаточно изменить знаки в целевой функции на противоположные и найти решение задачи при .

2.2. Общая задача линейного программирования

Общая задача линейного программирования заключается в поиске среди неотрицательных решений системы линейных алгебраических уравнений

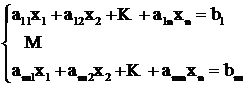(2.6)

такого, которое обеспечивает минимум линейной функции

В матричном виде: ,

(2.7)

Здесь:

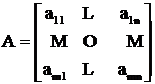– матрица условий задачи,

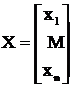– вектор неизвестных,

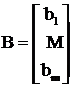– вектор правой части,

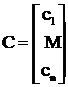– вектор коэффициентов целевой функции.

2.3. Алгебра линейного программирования

Напомним некоторые сведения из линейной алгебры, необходимые для понимания линейного программирования.

2.3.1. Операции над матрицами

Пусть А – матрица размерностью (m – строк и n – столбцов).

Транспонирование . Для нахождения транспонированной матрицы у исходной матрицы строки заменяются столбцами и наоборот. Пример:

Обратная матрица: .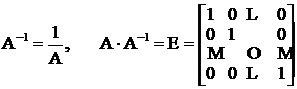

Минором элемента определителя D n-го порядка называется определитель (n–1)-го порядка, получающийся из D вычёркиванием i-й строки и j-го столбца.

Алгебраическим дополнением Aij элемента называется его минор, взятый со знаком (–1)i+j:

Aij=(–1)i+j Mij

Число миноров k-го порядка для матрицы условий задачи A размером m´n определяется числом сочетаний :

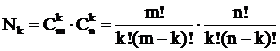Пример. Определить число миноров 1-го и 2-го порядков для матрицы А 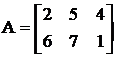N1=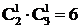 – это сами элементы матрицы А;

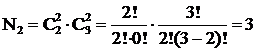. Вот эти три минора , , .

2.3.2. Система алгебраических уравнений

В матричной форме система линейных алгебраических уравнений (СЛАУ) имеет вид

А Х=В,

где

, , .

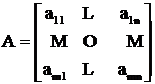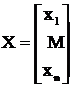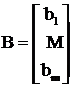Эта же система в алгебраической форме имеет вид:

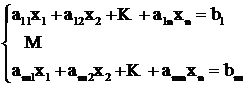
В зависимости от соотношения m и n возможны следующие случаи:

1) и определитель матрицы . В этом случае система совместна и имеет единственное решение.

Решение можно найти по правилу Крамера: ,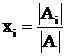

где Аi – исходная матрица, в которой i-ый столбик заменен правой частью

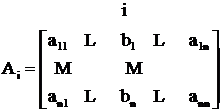Для решения могут использоваться и многочисленные другие методы.

При система несовместна, т. е. не имеет решений.

2) . Как правило, система несовместна так как уравнений больше, чем неизвестных.

3) . Система совместна, если ранг исходной матрицы и ранг расширенной матрицы совпадают (теорема Кронеккера-Капелли).

Как известно, рангом матрицы называют наивысший порядок отличных от нуля миноров этой матрицы. Ранг определяет число линейно независимых строк (столбцов) в матрице, если их рассматривать как вектора. Строка а1, а2, …, аm линейно независима, если можно подобрать такие числа l1, l2, …, lm не равные нулю одновременно, что

Если это равенство имеет место только при всех li = 0, то строки а1, а2, …, аm линейно независимы.

Например, строки а1=(1, 2, 3) и а2=(2, 4, 6) линейно зависимы, так как при l1 = 2 и l2 = –1 выполняется условие .

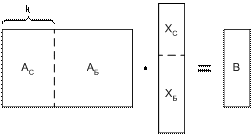
Если матрица А условий задачи состоит из линейно независимых уравнений, то её ранг r(A)=m. Расширенная матрица В получается из А добавлением столбца правых частей вi. При r(A) = r(B) система совместна и имеет бесконечное множество решений. Найти решения можно, если матрицу А разделить на блоки, выделив базисный минор АБ, и оставшийся блок АС. Соответственно делится и вектор Х на базисные ХБ и свободные ХС переменные (рис. 2.1).

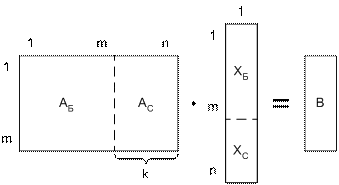
Рис. 2.1

Тогда по правилам выполнения операций с блочными матрицами можно записать 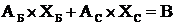. Откуда можно получить выражения, позволяющие линейно выразить базисные переменные через свободные .

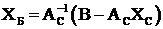Свободные переменные ХС могут принимать любые положительные значения, что позволяет однозначно определять и значения базисных переменных, т. е. находить полное решение СЛАУ.

Число таких решений бесконечно. Среди них существуют и недопустимые, в которых одна или несколько базисных становятся отрицательными.

Решение, в котором , называют базисным.

Поскольку в качестве свободных могут использоваться любые k неизвестных из n, то число базисных решений определяется числом сочетаний из n по k .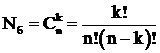

2.4. Геометрия линейного программирования

Рассмотрим геометрический смысл задачи линейного программирования.

В алгебраической форме задача формулируется следующим образом.

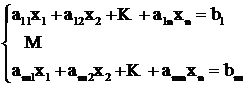(2.8)

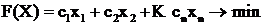Рассмотрим одно уравнение: 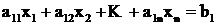. Геометрическим местом точек хi, являющихся решением уравнения, будет некая гиперплоскость, вырождающаяся при n = 2 в прямую, а при n = 3 в плоскость. Эта гиперплоскость делит пространство на два полупространства. Решением системы неравенств является пересечение полупространств, образующее выпуклую область. Выпуклая область – такая область, в которой для двух точек, принадлежащих области, отрезок, их соединяющий, полностью принадлежит ей (рис. 2.2).

Рис. 2.2

Пример. Определить допустимую область для системы неравенств.

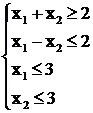(2.9)

На рис. 2.3 показаны допустимые полуплоскости для всех неравенств, отмеченных номерами. Допустимая область образует выпуклый многоугольник АВСDЕ.

В общем случае, геометрическим местом точек, являющихся решением системы линейных уравнений или неравенств будет выпуклый многогранник, образованный пересечением линейных гиперплоскостей.

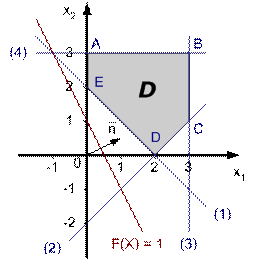
Рис. 2.3

Определим теперь геометрический смысл целевой функции F(Х).

Рассмотрим две гиперплоскости разных значений целевой функции и получившуюся систему из 2-х уравнений:

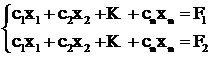
Проверим совместность этой системы по теореме Кронеккера-Капелли.

Ранг основной матрицы системы равен r = 1, т. к. любой определитель второго порядка равен 0.

В расширенной же матрице всегда можно найти определитель второго порядка, включающий добавленный столбец со значениями и , отличный от 0. Значит ранг расширенной матрицы равен 2.

Таким образом, ранги и не равны и система не имеет решений. Следовательно, гиперплоскости разных значений целевой функции не пересекаются, т. е. они образуют семейство параллельных гиперплоскостей.

В связи с этим решение задачи линейного программирования находится там, где допустимая область касается гиперплоскости наименьшего значения целевой функции.

В рассмотренном выше примере для допустимой области (см. рис. 2.3) введем целевую функцию . При n = 2 целевая функция F представляется семейством параллельных прямых. Направление прямой F(X)=const можно определить по нормали, координаты которой равны коэффициентами при неизвестных, т. е. вектор нормали 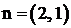. Минимум целевой функции достигается в точке Е при .

Таким образом, решение задачи линейного программирования всегда лежит на границе допустимой области и, как правило, в вершине многогранника, иногда на ребре, а в редких случаях – на грани.

Как искать решение, лежащее на границе допустимой области? Методы поиска, основанные на производных, здесь не работают, т. к. на границе не существует понятия производной. В 1947 году американский математик Данциг предложил симплекс-метод, который основан на последовательном обходе вершин многогранника допустимых решений, начиная с произвольно выбранной, в направлении снижения целевой функции.

Алгебраически каждая вершина многогранника соответствует какому-либо базисному решению, в котором соответствующие ему свободные переменные равны нулю. Переход к соседней вершине осуществляется путем замены только одной свободной переменной на соответствующую базисную и перевода этой базисной в список свободных.

2.5. Идея симплекс-метода

Идею и суть симплекс-метода рассмотрим на примере следующей задачи линейного программирования

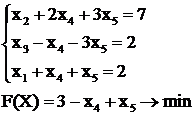(2.10)

Все уравнения задачи линейно независимы, ранги матрицы системы и расширенной равны 3, следовательно, система совместна. Примем в качестве свободных переменных х4 и х5.

Выразим базисные переменные х1, х2, х3 через свободные:

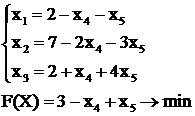(2.11)

Базисное решение: , F(Х) = 3 является допустимым.

Проанализируем возможности уменьшения целевой функции. При этом имеет смысл рассматривать изменение х4, х5 только в сторону их увеличения, так как в линейном программировании переменные не могут быть отрицательными.

Перед х4 в формуле F(X) стоит знак «–». Следовательно, для снижения F(X) выгодно увеличивать х4. Переменную х5 = 0 изменять невыгодно, так как любое ее увеличение приведет только к росту целевой функции.

Оценим поведение базисных переменных х1, х2, х3 при росте х4. Очевидно, что при этом х3 возрастает, а х1 и х2 уменьшаются и могут перейти в недопустимую область, где .

Проанализируем х1 и х2, чтобы определить, которая из них скорее станет равной нулю при увеличении х4. При зависимости этих базисных от х4 будут 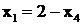и 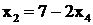, откуда следует, что при , а при . Значит рост х4 будет ограничиваться значением 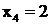, при котором базисная переменная х1 станет равной 0, а х2 останется положительной равной 3.

В новом решении , , 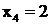, состав свободных изменился. Выразим базисные через новый набор свободных х5 и х1:

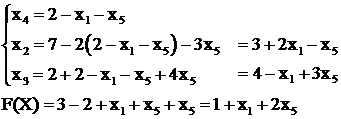(2.12)

При этом новое базисное решение: , , , , .

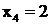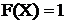Дальнейший анализ получившегося базисного решения нужно проводить таким же образом. В данном случае свободные переменные входят в целевую функцию с положительными знаками, следовательно, дальнейших возможностей по уменьшению целевой функции нет. Значит, полученное решение является оптимальным.

2.6. Алгебра симплекс-метода

Основная задача линейного программирования в матричной форме:

(2.13)

Выберем произвольно первое базисное решение, приняв в качестве свободных первые неизвестных. Будем считать, что оно допустимо. Выразим базисные переменные и целевую функцию F через свободные. Для этого разделим матрицу А и вектора Х и В на соответствующие блоки (рис. 2.4).

Рис. 2.4

По правилам операций над блочными матрицами запишем

откуда .

Аналогичное выражение для целевой функции

Запишем матричные выражения для базисных переменных и целевую функцию в алгебраической форме:

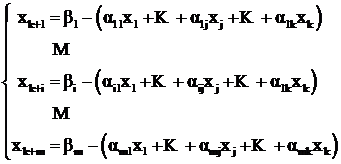, (2.14)

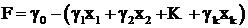Эту форму записи называют стандартной.

Рассмотрим базисное решение, в котором все свободные . Значения базисных переменных . Полагаем, что все , т. е. базисное решение 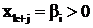допустимо. При этом целевая функция .

Рассмотрим внимательнее полученное базисное решение и оценим пути уменьшения целевой функции. Здесь возможны следующие ситуации:

1) γj<0 для всех j=1,…,k.

В этом случае увеличение любой свободной переменной от нуля приводит к росту целевой функции. Следовательно, рассматриваемое базисное решение является оптимальным.

2) γj>0 (хотя бы для одного j), а все .

При этом рост хj, приводящий к снижению целевой функции, сопровождается ростом всех базисных переменных, которые сохраняют свою допустимость. При этом 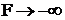. Этот случай носит чисто теоретический характер. В практических задачах подобная ситуация возможна только при некорректной математической модели.

3) γj>0 для одного или нескольких j и для нескольких i.

В этом случае увеличение хj сопровождается уменьшением тех базисных, для которых , а зависимость от хj определяется уравнением . Каждая из этих базисных подходит к границе допустимой области, определяемой условием при значении . Из всех этих значений выберем минимальное и присвоим ему индекс i

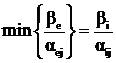Это значение определяет допустимую для роста величину хj, при которой из всех убывающих базисных первая становится равной нулю.

Коэффициент имеет важное значение, и его называют генеральным.

При этом снижение целевой функции определяется произведением

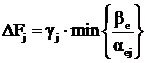В том случае, если есть несколько , генеральный элемент должен для ускорения решения выбираться из следующего условия:

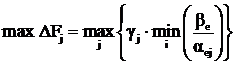. (2.15)

После поиска генерального элемента, определяющего по сути пару переменных и , делается переход к новому базисному решению. В новом наборе свободных переменных хk+i заменяет хj, которая переходит в список базисных на место хk+i, т. е. эти две переменные меняются местами в списках свободных и базисных.

Таким образом, изменившийся набор свободных включает

Найдем выражение базисных и формы F через новый набор свободных переменных. Для этого из выражения для исключаемой базисной

(2.16)

найдём значение свободной xj

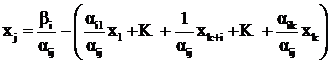. (2.17)

Подставим это выражение во все остальные базисные и проведем необходимые преобразования

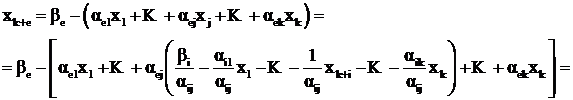
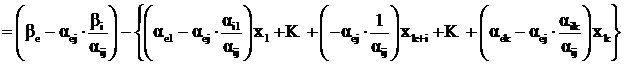(2.18)

Аналогично преобразуется и целевая функция, но при этом в формуле вместо участвует , а вместо

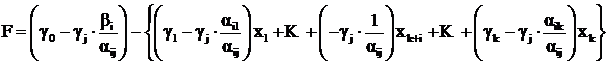. (2.19)

Рассмотрим полученное базисное решение. Все свободные принимаются равными нулю .

При этом базисные переменные будут равны:

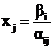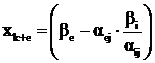
и целевая функция

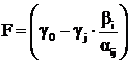Проверим решение на допустимость. Базисная переменная , так как в исходном базисном решении и .

Рассмотрим остальные базисные . Здесь характер изменения определяется знаком αej. При αej<0 базисная переменная возрастает, оставаясь положительной. При αej>0 значение базисной уменьшается. Для анализа преобразуем зависимость к виду

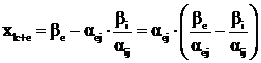по которому следует, что хk+e будет оставаться положительной, так как генеральный элемент выбирается по условию .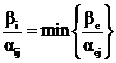

Таким образом, полученное в результате проведенных преобразований новое базисное решение остаётся допустимым.

Оценим теперь изменение целевой функции, равной в новом базисе

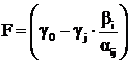Здесь все коэффициенты, определяющие приращение функции, положительны, что приводит к снижению функции на величину .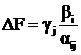

Переход к новому базису достаточно просто формализуется с помощью специальных симплекс-таблиц.

2.7. Правила работы с симплекс-таблицей

Симплекс-таблица строится для допустимого базисного решения. В ней столбцы соответствуют свободным переменным, строки – базисным и линейной форме, а в верхние половинки образовавшихся клеток таблицы записываются коэффициенты, которые соответствуют выражению базисных переменных и формы через свободные.

Таблица 2.2