Исследование операций (стр. 7 )

В качестве примера рассмотрим возможные состояния подстанции из двух трансформаторов. Здесь возможны всего четыре состояния:

– оба трансформатора работают,

– Т1 в ремонте, Т2 работает,

– Т2 в ремонте, Т1 работает,

– оба трансформатора в ремонте.

Состояния и переходы между ними удобно анализировать с помощью графа состояний, в котором состояния изображаются квадратами, кругами или прямоугольниками, а возможные переходы из состояния в состояние – стрелками, их соединяющими.

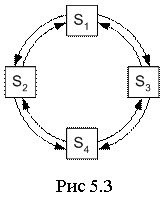На рис. 5.3 показан граф состояния для рассмотренной подстанции. Стрелки определяют переходы в момент отказа оборудования и ввода его после ремонта.

Для построения математических моделей марковских случайных процессов введем некоторые понятия, характеризующие вид и характер процесса.

Поток событий – последовательность однотипных событий, следующих одно за другим в случайные моменты времени. Например: поток отказов оборудования; поток составов с топливом, поступающих на ТЭС; поток бытовых электроприборов, включаемых в сеть и т. п.

Каждый поток событий характеризуется интенсивностью . Интенсивность – среднее число случайных событий, которые приходятся на единицу времени. Она определяет и вероятность наступления событий. Интенсивность потока может быть постоянной и переменной, зависящей от времени.

Поток событий называется регулярным, если события происходят через одинаковые промежутки времени.

Часто интервалы между событиями также меняются случайно, но на большом отрезке времени число событий может быть относительно стабильным.

Стационарный поток событий – такой, у которого и не зависит от времени. Часто фактическое значение меняется, но без определенных закономерностей. При этом среднее число событий в единицу времени постоянно. Отклонения от стационарности возможны из-за многих причин. Так поток включения бытовых приборов в течении суток не стационарен, а на определенном отрезке суток может быть практически стационарен.

Поток без последействия – такой поток, у которого число событий на разных, но одинаковых по длине временных интервалах, не зависят друг от друга (рис. 5.4).

Это означает, что события в потоке появляются независимо друг от друга и вызваны своими собственными причинами.

Рис. 5.4

Поток событий называется ординарным, если события наступают по одному, а не группами одновременно. Так поток составов на ТЭС ординарен, а вагонов – неординарен.

Поток называется простейшим, если для него характерны следующие свойства: стационарность, ординарность, отсутствие последействия. Процессы, связанные с простейшими потоками, имеют наиболее простое математическое описание.

5.2. Уравнения Колмогорова для вероятностей состояний

Для простейшего потока событий вероятность наступления события на отрезке можно определить по следующей формуле:

(5.1)

Это позволяет проводить анализ процессов и определять вероятности разных состояний на основе системы уравнений Колмогорова.

Рассмотрим марковский случайный процесс с дискретным состоянием и непрерывным временем. В этом случае переход системы из одного состояния в другое определяется потоком случайных событий, где первое появляющееся событие приводит к переходу в другое состояние. Если все потоки событий простейшие, то процесс в системе будет марковским, т. к. в простейшем потоке нет последействия и «будущее» не зависит от «прошлого». Граф с направлениями переходов и проставленными интенсивностями у стрелок называют размеченным.

Составим размеченный граф для подстанции с двумя трансформаторами (рис. 5.5).

Состояния этой системы уже рассматривались и обозначают:

– оба трансформатора работают,

– Т1 в ремонте, Т2 работает,

– Т2 в ремонте, Т1 работает,

– оба трансформатора в ремонте.

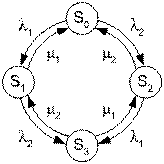
Рис. 5.5

Интенсивности, показанные на рис. 5.5, характеризуют следующие потоки событий:

– аварийного выхода Т1,

– аварийного выхода Т2,

– потока окончания ремонта Т1,

– потока окончания ремонта Т2.

Интенсивности потока отказов определяются как величины, обратные средней продолжительности безотказной работы. Интенсивности являются обратной величиной средней продолжительности ремонта.

По размеченному графу можно построить математическую модель, которая позволит оценить вероятности всех возможных состояний и изменение их во времени. Назовем вероятностью i-го состояния вероятность того, что в момент t система будет находиться в состоянии , т. е. – вероятности состояний .

Очевидно, что для любого момента справедливо условие .

Для нахождения всех формируется специальная система дифференциальных уравнений, называемых уравнениями Колмогорова.

Рассмотрим порядок составления этих уравнений для некоторой системы, имеющей четыре возможных состояния S1, S2, S3, S4. Размеченный граф системы показан на рис. 5.6.

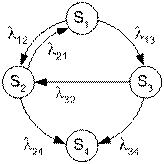
Рис. 5.6

Предположим, что в произвольный момент времени t система находится в состоянии S1, вероятность которого . Рассмотрим небольшой промежуток времени и найдем вероятность того, что система к моменту будет находиться в том же состоянии S1. Это возможно в двух случаях:

1) В момент t система была в состоянии S1 и за время не состоялся переход ее ни во второе, ни в третье состояние. Вероятность перехода из состояния S1 определяется вероятностью двух несовместных событий, равной . Вероятность того, что система не выйдет из состояния S1 будет равна .

2) В момент t система была в состоянии S2 и за время состоялся переход из состояния S2 в S1, вероятность которого . Вероятность второго случая определяется произведением вероятностей .

Общая вероятность того, что к моменту система будет в состоянии S1:

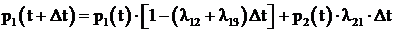. (5.2)

Преобразуем это выражение:

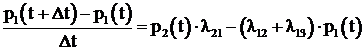(5.3)

Слева имеем приращение функции отнесенное к приращению аргумента . Предел этого отношения при есть производная

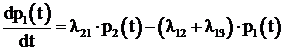. (5.4)

Аналогично формируются дифференциальные уравнения для вероятностей остальных состояний:

,

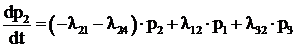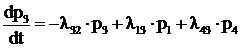, (5.5)

.

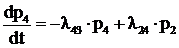Таким образом получена система из четырех линейных дифференциальных уравнений с четырьмя неизвестными функциями времени , , , .

Для получения решения одно из этих уравнений нужно заменить на очевидное условие , справедливое в любой момент времени. Кроме того, решение системы дифференциальных уравнений требует задания начальных условий, например, равных , .

Для решения системы могут использоваться численные методы, ориентированные на применение ЭВМ.

Система уравнений Колмогорова формируется по следующим правилам.

В левой части уравнений стоят производные вероятностей i-х состояний.

В правой части – сумма произведений вероятностей всех состояний, из которых ведут стрелки в рассматриваемое состояние, на интенсивность соответствующих потоков событий, минус суммарная интенсивность потоков событий, выводящих систему из этого i-го состояния, на его вероятность.

Применим это правило и составим уравнения Колмогорова для подстанции с двумя трансформаторами (см. рис. 5.5):

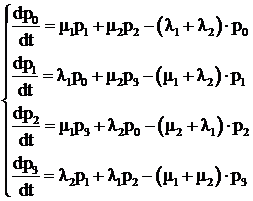(5.6)

Решение системы дифференциальных уравнений позволяет найти вероятности всех состояний системы в любой момент времени. Определенный интерес представляет решение при 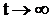, когда процесс устанавливается и все производные стремятся к нулю. При этом получается система линейных алгебраических уравнений. Вероятности, определяемые этой системой, называют финальными вероятностями состояний. Их можно толковать как среднее относительное время пребывания в определенном состоянии.

Найдем финальные вероятности состояний для рассмотренного примера.

Система алгебраических уравнений, соответствующая (5.6), имеет вид:

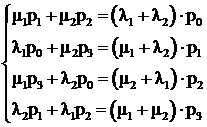(5.7)

Эту систему можно составить по следующему правилу: для каждого состояния сумма членов, соответствующих входящим стрелкам, равна сумме членов, соответствующих выходящим.

Эта система уравнений (5.7) не имеет свободного члена и может решаться, как уже отмечалось, если одно из уравнений заменить нормирующим условием:

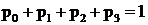(5.8)

Для примера определим финальные вероятности для следующих интенсивностей потоков:

.

Заменим четвертое уравнение условием (5.8)

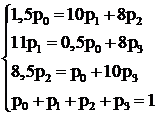(5.9)

Решив систему, получим: , , , .

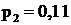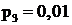Анализ решения показывает, что подстанция в среднем 85% расчетного времени будет находиться в рабочем состоянии, 4% – в состоянии S1, когда ремонтируется трансформатор Т1, 11% – в состоянии S2 при ремонте Т2 и лишь 1% в состоянии S3, когда оба трансформатора в ремонте.

Полученные финальные вероятности объясняются принятыми интенсивностями, по которым трансформатор Т1 имеет более высокую аварийность и продолжительность ремонта.

Финальные вероятности можно использовать для оценки экономической эффективности работы подстанции путем расчета, например, математического ожидания дохода за расчетный период. Предположим, что работа в состоянии S0 приносит в единицу времени доход d0, в состоянии S1 – доход d1, в состоянии S2 – d2, а в состоянии S3 – штрафные санкции – d3. При этом d0 > d1 > d2, а d3 < 0.

Тогда математическое ожидание дохода за расчетный период Т:

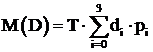(5.10)

При этом появляется возможность оценить целесообразность дополнительных затрат в организацию ремонта трансформаторов, эффективность диагностики и других мероприятий по обслуживанию объекта.

Глава 6. Статистическое моделирование случайных

процессов

6.1. Метод статических испытаний

На практике марковские или близкие к ним случайные процессы встречаются далеко не всегда. Для большинства потоков событий, меняющих состояние системы, адекватные математические модели не существуют.

В подобных случаях, когда построение математического описания процесса связано с большими трудностями или вообще невозможно, применяется другой метод моделирования, известный под названием метода статистических испытаний или метода Монте-Карло.

Идея метода достаточно проста. Вместо описания случайного явления с помощью математических зависимостей, осуществляется «розыгрыш» – моделирование случайного процесса с помощью некоторой процедуры, дающей случайный результат. При этом мы получаем одну реализацию случайного явления, одно случайное событие в общем потоке. Повторяя такой розыгрыш много раз, мы получим богатый статистический материал, который можно обработать методами теории вероятности и математической статистики.

Часто такой подход оказывается значительно проще, чем поиск путей построения математического описания для исследования явления. Для сложных операций в больших системах метод статистических испытаний может оказаться единственно возможным.

Рассмотрим простой пример. Питание установки электроэнергией осуществляется по двум параллельным цепям. Вероятность нерабочего состояния каждой . Заметим, что таких низких показателей надежности для современных линий электропередач не существует и такой показатель взят лишь для иллюстрации идеи метода. Определим вероятность потери питания.

Эта простая задача без труда может быть решена и аналитически. Вероятность потери питания будет определяться вероятностью одновременного выхода двух цепей, равной .

Теперь попробуем решить задачу путем «розыгрыша».

Будем моделировать поток случайных событий, который воздействует на ЛЭП в процессе эксплуатации, другой случайной процедурой – бросанием двух монет: появление герба будет условно обозначать нормальную работу, а решки – аварийное отключение и ремонт.

Если при бросании двух монет появится два или хотя бы один герб, то условно это будет соответствовать подаче питания по двум или по одной цепи, а появление двух решек – потере питания.

Повторив такой «опыт», состоящий в бросании двух монет большое число раз N, и подсчитав число одновременных выпадений двух решек М, и поделив М на N, мы почти наверняка получим число, близкое к 0.25.

В этом примере интересующую вероятность можно было определить на основе элементарных представлений из теории вероятностей, т. е. гораздо проще, чем по методу Монте-Карло.

Рассмотрим другой пример, взятый из [1]. Пусть производится бомбометание по некоторой цели. Зона разрушительного действия бомбы имеет вид круга с радиусом R. Сбрасывается четыре бомбы. Для вывода цели из строя нужно покрыть не менее k % площади её. Требуется найти вероятность поражения цели.

Для этой задачи, простой на вид, получение аналитического решения достаточно сложно. Проще получить решение путем «розыгрыша». Для этого надо разыграть координаты попадания 4-х точек, вокруг каждой описать круг радиуса R и подсчитать общую пораженную площадь цели. Если эта площадь больше или равна k % общей площади цели, то это соответствует поражению цели, если меньше – то цель не поражена.

Рассмотрим далее способы организации единичного испытания.

6.2. Методы формирования случая

Основным элементом метода Монте-Карло является одна случайная реализация исследуемого процесса, например, аварийный выход установки, сбрасывание бомбы, появления посетителя, запрос на выдачу справки и т. п.

Случайная реализация разыгрывается с помощью специального алгоритма, в котором важную роль играет «розыгрыш» или «бросание жребия».

Единичным жребием называют любой элементарный опыт, в котором дается ответ на один из вопросов:

1.  Произошло или нет событие А?

2.  Какое из событий А1, А2, …, Аn произошло?

3.  Какое значение приняла случайная величина х?

4.  Какую совокупность значений приняла система случайных величин
х1, х2, …, хn?

Единичный жребий любой разновидности можно осуществить на основе генерации случайного числа R, имеющего равномерное распределение на отрезке от 0 до 1.

1. Произошло или нет событие А?

Для этого надо знать вероятность р наступления события. Розыгрыш случайного числа R и проверка условия позволяют ответить на этот вопрос: если условие выполнено, то событие А произошло, иначе событие А не состоялось.

2. Какое из событий А1, А2, …, Аn произошло?

Полагаем, что эти события несовместны и образуют полную группу, т. е. сумма их вероятностей р1, р2, …, рn равна единице. Интервал (0, 1) делится на n участков (рис. 6.1). Свершившееся событие определяется участком, на который попало случайное число R.

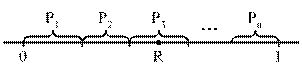
Рис. 6.1

3. Какое значение приняла случайная величина х?

Если случайная величина х дискретна и может принимать значения х1, х2, …, хn с вероятностями р1, р2, …, рn, то выпадающее значение х определяется как и в предыдущем случае.

Интерес представляет случай, когда случайная величина х непрерывна и задана плотностью распределения f(x). Например, график плотности случайной величины х, имеющей нормальное распределение в интервале показан на рис. 6.2, а. Заметим, что площадь, ограниченная графиком, равна единице. С помощью этого графика можно определить вероятность того, что случайная величина х будет меньше величины а. Эта вероятность 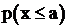определяется заштрихованной площадью.

Для определения вероятности 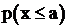удобнее использовать функцию распределения F(x), график которой показан на рис. 6.2, б.

Функция распределения F(x) и плотность распределения связаны формулой

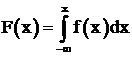. (6.1)

По кривой F(x) можно определить вероятность 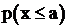(см. рис. 6.2, б).

Случайную величину х можно найти по розыгрышу R путем поиска такого значения х, при котором F(x) = R.

На практике часто используется нормальное распределение случайных величин. Для облегчения расчетов при работе с нормальным законом распределения переходят от реальной случайной величины х к нормированной случайной величине:

, (6.2)

где – математическое ожидание,

– стандартное отклонение.

При этом вероятность случайной величины х не превышающей а будет:

, (6.3)

где .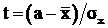

Для определения Ф(t) имеются специальные таблицы.

Розыгрыш значения случайной величины х, меняющейся по закону нормального распределения, осуществляется сложением шести реализаций случайных чисел

. (6.4)

Полученное z имеет распределение достаточно близкое к нормальному. Для обеспечения заданного значения математического ожидания и стандартного отклонения величину z преобразуют

. (6.5)

4. Какую совокупность значений приняли случайные величины х1, …, хn?

Если случайные величины независимы, то необходимо n раз повторить процедуру, рассмотренную в предыдущем пункте.

Таким образом, все четыре варианта единичного жребия сводятся к розыгрышу случайного числа R равномерно распределенного на отрезке от 0 до 1.

Сегодня известно несколько разновидностей датчиков случайных чисел.

Самый простой способ – лототрон, или барабан с пронумерованными шариками.

Для розыгрыша случайного числа R могут использоваться подготовленные таблицы случайных чисел, которые часто приводятся в руководствах по теории вероятностей.

Сегодня для статистического моделирования широко применяются ЭВМ, в которых для розыгрыша R используются специальные датчики. Они могут генерировать случайные числа на основе физических устройств, преобразующих случайные шумы, либо на основе специальных алгоритмов, запуск которых чаще всего определяется случайным моментом времени.

Эти программы называют генераторами «псевдослучайных чисел». Один из простых алгоритмов формируется следующим образом: берутся два произвольных n-значных числа а1 и а2, перемножаются и в полученном произведении выбираются n средних знаков, образующих число a3. Затем перемножают a2 и а3, после чего выбирают из середины число а4 и т. д.

6.3. Пример моделирования случайного процесса методом Монте-Карло

Рассмотрим задачу определения вероятности аварийного выхода мощности Р0 = 100 МВт для энергосистемы, в составе которой работают два блока по 100 МВт, имеющих вероятность аварийного состояния q1 = 0,1 и три блока по 50 МВт с вероятностью аварийного состояния q2 = 0,15.

Аварийный выход мощности 100 МВт возможен при двух независимых и несовместных случайных событиях:

1) аварийный выход блока 100 МВт при рабочем состоянии всех остальных,

2) аварийный выход двух блоков из трех по 50 МВт при работе всех блоков по 100 МВт.

Наступление события – аварийного выхода каждого блока будем определять по условию 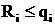, для чего потребуется генерация пяти случайных чисел.

Для каждого испытания всех блоков системы необходимо определить суммарную величину аварийно отключаемых блоков и отсчитывать число испытаний с выходом мощности Р0 = 100 МВт. Вероятность дефицита определяется 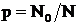, где N – общее число испытаний, N0 – число розыгрышей, в которых дефицит равен 100 МВт.

Алгоритм статистических испытаний приведен на рис. 6.3.

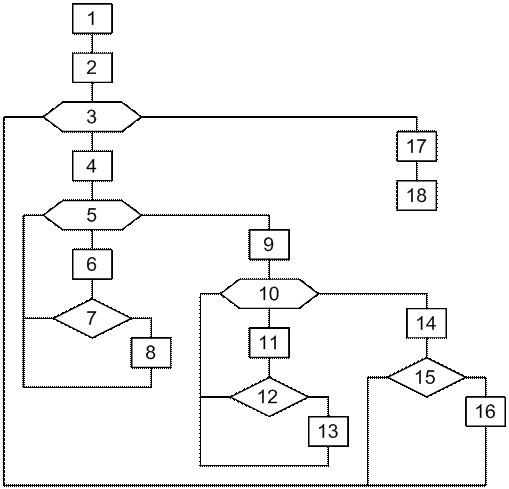
Рис. 6.3

Функции, выполняемые в блоках алгоритма:

1 – ввод исходных данных: n1, q1, n2, q2, N,

2 – установка счетчика N0 = 0,

3 – цикл по испытаниям,

4 – установка счетчика выхода блоков 100 МВт к1 = 0,

5 – цикл по блокам 100 МВт,

6 – генерация R1,

7 – проверка условия ,

8 – к1 = к1 + 1,

9 – установка счетчика к2 = 0,

10 – цикл по блокам 50 МВт,

11 – генерация R2,

12 – проверка условия ,

13 – к2 = к2 + 1,

14 – вычисление аварийного выхода ,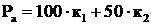

15 – сравнение Ра = Р0,

16 – N0 = N0 + 1,

17 – расчет вероятности ,

18 – вывод результатов.

На рис. 6.4 приведена диаграмма, реализующая рассмотренный алгоритм в среде программирования LabVIEW. На диаграмме показаны три цикла: 7 – внешний по числу испытаний, и два внутренних 8 и 9, соответственно, по блокам 100 и 50 МВт.

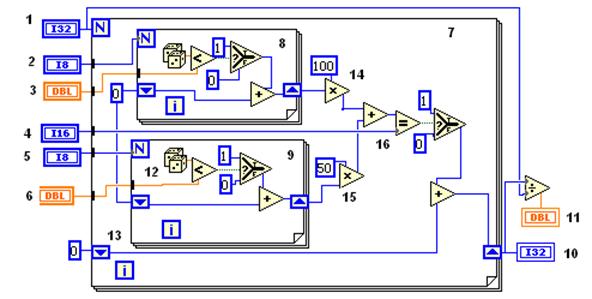
Рис. 6.4

Задатчики исходных данных отмечены следующими номерами:

1 – число испытаний;

2 – число блоков первой группы;

3 – вероятность аварийного состояния блоков этой группы;

5, 6 – аналогичные данные по второй группе;

4 – значение дефицита мощности Р0.

Основные результаты выдаются на индикаторы:

10 – число розыгрышей, в которых дефицит равен Р0;

11 – вероятность дефицита.

Остальные номера элементов программы обозначают:

12 – генератор псевдослучайных чисел;

13 – счетчик испытаний;

14, 15 – определение мощности отключенных блоков, соответственно, 100 и 50 МВт;

16 – сравнение мощности отключенных блоков с Р0.

Результаты проведения статистических испытаний представлены в табл. 6.1.

Таблица 6.1

В этом примере рассмотрена задача, которая может быть решена аналитически и без использования метода Монте-Карло на основе известной формулы Бернулли, полученной из разложения бинома (р + q)n. Формула позволяет найти вероятность аварийного выхода к агрегатов из n однотипных

, (6.6)

где – вероятность рабочего состояния.

В рассматриваемой системе работают две группы однотипных блоков. В этом случае вероятности всех возможных случайных состояний определяются произведением биномов

. (6.7)

Аварийный выход мощности 100 МВт возможен при двух несовместных и независимых случайных событиях. В первом событии аварийно отключается один блок 100 МВт при всех работающих блоках по 50 МВт. Во втором – аварийно отключается два блока по 50 МВт, а оба блока по 100 МВт остаются в работе.

Вероятность первого события определяется произведением вероятностей, характеризующих события в каждой из двух групп блоков

.

Вероятность второго события

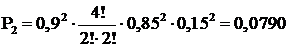
Общая вероятность аварийного выхода мощности 100 МВт

.

Глава 7. Игровые методы выбора решений

7.1. Предмет теории игр

В больших технико-экономических системах в силу двойственности природы наряду с закономерностями действуют многочисленные случайные факторы и неопределенности, когда некоторые параметры, которые во многом определяют результат операции, неизвестны и нет никакой информации, позволяющей оценить их значения.

Неопределенными могут быть внешние «объективные» условия операции и «субъективные» – сознательные действия противника, конкурентов или других лиц.

Конечно, в условиях неопределенности переоценивать и возлагать большие надежды на математический анализ вряд ли имеет смысл, но и в этом случае количественный анализ ситуации при выборе решения лучше, чем решение, которое принимается «с потолка».

Для принятия решения в подобных условиях используется специальный раздел математики, называемый «теорией игр». Основным предметом теории игр являются конфликтные ситуации, в которых сталкиваются интересы двух или более сторон, преследующих разные, часто противоречивые цели и успех каждой стороны зависит от действий другой.

Примеры конфликтных ситуаций весьма разнообразны. Это, конечно, боевые ситуации, ситуации на конкурентном рынке, широкий круг задач с участием «природы» с ее непредсказуемостью и т. п.

Каждая конкретная конфликтная ситуация достаточно сложна, имеет много «оттенков» и ее точный анализ практически невозможен. Для целей математического анализа строится математическая модель ситуации, которая и называется игрой.

От реальной ситуации игра отличается тем, что развивается по определенным правилам. Эти правила определяют порядок действий – ходов, исход игры – выигрыш или проигрыш каждого игрока в зависимости от обстановки.

Набор возможных ходов в игре называют стратегией. Стратегии бывают чистые, когда они выбираются по определенным правилам, и смешанные, когда они выбираются случайным образом.

Наиболее разработанной в теории игр является конечная парная игра с нулевой суммой, в которой участвуют два игрока А и В, причем выигрыш одного равен проигрышу другого. Для ясности анализа при выборе стратегий в игре себя мы будем ставить на место игрока А. Будем считать, что у нас имеется m возможных стратегий А1, А2, …, Аm, а у противника – n стратегий В1, В2, …, Вn. Такая игра называется игрой m×n.

Обозначим аij наш выигрыш в том случае, если мы пользуемся стратегией Ai, а противник – стратегией Вj.

Если такие выигрыши aij определены для каждой пары стратегий, то их можно представить в виде матрицы, называемой платежной.

Все основные сложности теории игр и заключаются в приведении игры к матричной форме.

Рассмотрим несколько примеров составления платежных матриц.

1. Игра «орел – решка»

Простейшая игра, в которой участвуют два игрока, и простейшая техника – монета.

Мы (игрок А) загадываем «орла» или «решку». Игрок В отгадывает, если он угадал, мы проиграли, не угадал – мы выиграли. Таким образом, у каждого игрока по две стратегии. Имеем игру 2×2. Платежная матрица приведена в табл. 7.1.

Таблица 7.1

2. Игра «три пальца»

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8