СОДЕРЖАНИЕ
Введение………………………………………………………………………...2
1. Распространение радиоволн в идеальном однородном диэлектрике ……3
2. Распространение плоских радиоволн в однородной проводящей средеПринцип Гюйгенса и зоны Френеля………………………………………..9
4. Отражение радиоволн от поверхности плоской Земли………………….13
5. Отражение плоских радиоволн на границе раздела двух сред………….15
5.1. Коэффициент отражения вертикально поляризованной волны…….. 16
5.2. Коэффициент отражения горизонтально поляризованной волны…… 18
6. Влияние шероховатости отражающей поверхности……………………..19
7. Распространение радиоволн при наличии экранирующих препятствий.21
7.1. Эффект "усиления препятствем".……………………………………….22
8. Распространение радиоволн при антеннах, поднятых над плоской
Землей ………………………………………………………………………23
8.1. Горизонтальная поляризация падающей волны………………………..25
8.2. Вертикальная поляризация падающей волны..………………………..26
9. Поверхностное распространение радиоволн……………………………..28
10. Напряжённость поля радиоволны, распространяющейся вдоль земной
поверхности.. …………………………...………………………………...31
10.1."Взлетная" и "посадочная" площадки ……………………….………..32
10.2. Распространение радиоволн вдоль неоднородной трассы..…………33
10.3. Береговая рефракция..………………………………………………….34
11. Влияние сферичности отражающей поверхности………………………35
12. Распространение радиоволн в тропосфере..……………………………38
12.1. Атмосферная рефракция………………………………………………..39
12.2. «Эквивалентный» радиус Земли……………………………………….41
12.3. Виды атмосферной рефракции…………………………………………41
12.4. Флуктуации радиосигнала и многолучевость распространения…….44
12.5. Рассеяние УКВ на турбулентных неоднородностях.. ………………46
12.6. Полоса пропускания тропосферного канала…………………………48
12.7. Поглощение радиоволн в тропосфере…………………………………49
13. Распространение радиоволн в ионосфере ……………………………..50
13.1. Образование и строение ионосферы…………………………………..50
13.2. Преломление радиоволн в ионосфере ………………………………..52
13.3. Влияние магнитного поля на распространение радиоволн в
ионосфере ………………………………………………………………55
13.4. Эффект Фарадея ……………………………………………………….58
13.5. Распространение радиоволн в простом ионосферном слое…………58
13.6. Теоремы эквивалентности …………………………………………….60
13.7. Вертикальное зондирование ионосферы ……………………………63
13.8. Поглощение в ионосфере …………………………………………….64
Литература ……………………………………………………………………65
 |
ВВЕДЕНИЕ
В реальных условиях наличие хорошо проводящих поверхностей, а также неоднородностей различного происхождения как на Земле, так и в атмосфере, существенно искажает прямолинейное распространение радиоволн. Токи, наведенные в поверхности, вызывают поглощение энергии и дифракцию радиоволн.
Дифракция - отклонение распространения радиоволн от прямолинейного, обусловленное наличием препятствий на их пути. Чем больше длина волны, тем больше напряженность поля в области тени.
Рефракция - отклонение распространения радиоволн от прямолинейного, обусловленное изменением диэлектрической проницаемости e среды на пути распространения.
Степень влияния атмосферных и поверхностных факторов на распространение радиоволн существенно зависит от используемого диапазона.
В тропосфере с высотой изменяются давление, температура, влажность, что вызывает рефракцию радиоволн. Наличие в тропосфере случайных неоднородностей турбулентного происхождения приводит к рассеянию радиоволн и, как следствие, к возможности их распространения далеко за пределы прямой видимости.
В стратосфере распространение радиоволн аналогично тропосферному, однако эффекты атмосферного влияния выражены значительно слабее.
Ионосфера оказывает существенное влияние на распространение радиоволн. Так, радиоволны с l>10 м обычно отражаются от ионосферных слоёв и возвращаются на расстоянии до 3500 км от точки излучения, затем отражаются от Земли и т. д., то есть могут распространяться скачками на большие расстояния, вплоть до кругосветного. В диапазоне УКВ ионосфера прозрачна, и радиолуч уходит в космос, однако часть его энергии рассеивается различными ионосферными неоднородностями (метеорные следы, турбулентные неоднородности, спорадические слои и т. д.).
Общий вид системы уравнений Максвелла:
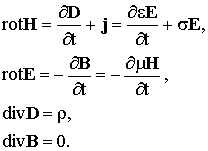 (1.1)
(1.1)
1. Распространение радиоволн в идеальном однородном диэлектрике
В такой среде e, m = Const, r = s = 0. Модель наиболее близка к распространению в нейтральной атмосфере. Для воздуха можно полагать, что магнитная проницаемость m = m0 = 4p×10-7 Гн / м, а диэлектрическая проницаемость e = e' e0 (e0 = 8,85×10-12 Ф / м, e¢ - относительная диэлектрическая проницаемость). Тогда система (1.1) принимает вид
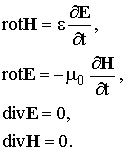 (1.2)
(1.2)
Выведем уравнение, описывающее распространение радиоволн в такой среде. Применим к двум первым уравнениям (1.2) операцию rot:
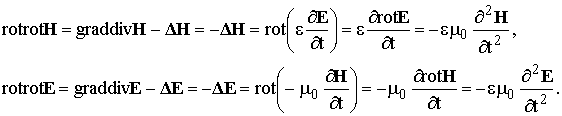
Получаем два дифференциальных уравнения второго порядка:
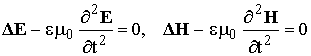 , (1.3)
, (1.3)
Будем полагать, что ток в излучающей антенне меняется по гармоническому закону, т. е. E, H ~ Cos wt (w - круговая частота), или в комплексной форме ![]() . Из представления напряжённости электрического поля E(r,t) = E(r)×eiwt следует, что
. Из представления напряжённости электрического поля E(r,t) = E(r)×eiwt следует, что 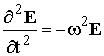 , аналогичное соотношение получается и для H. Подстановка в (1.3) даёт
, аналогичное соотношение получается и для H. Подстановка в (1.3) даёт
![]() , (1.4)
, (1.4)
где введено обозначение ![]() .
.
Из электродинамики известно, что физически корректным и математически точным решением волнового уравнения вида (1.3) является распространяющаяся от источника сферическая волна, амплитуда которой ![]() (r – расстояние от излучателя). При решении многих задач распространения рассматриваются плоские радиоволны, которые определяются следующим образом: электромагнитная волна называется плоской, если вектор напряженности электрического (магнитного) поля имеет одну и ту же величину во всех точках любой плоскости, перпендикулярной направлению распространения волны. Такая плоскость, следовательно, является и поверхностью равных фаз.
(r – расстояние от излучателя). При решении многих задач распространения рассматриваются плоские радиоволны, которые определяются следующим образом: электромагнитная волна называется плоской, если вектор напряженности электрического (магнитного) поля имеет одну и ту же величину во всех точках любой плоскости, перпендикулярной направлению распространения волны. Такая плоскость, следовательно, является и поверхностью равных фаз.
Пусть плоская радиоволна распространяется вдоль оси Ox, т. е. E = E(x, t), H = H(x, t). После подстановки этих представлений в (1.4) и сокращения на временной множитель eiwt получим
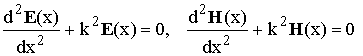 . (1.5)
. (1.5)
Нетрудно проверить, что решения уравнений (1.5) для волны, распространяющейся в положительном направлении Ox, имеют вид
E(x) = Em×e-ikx, H(x) = Hm×e-ikx, (1.6)
где Em и Hm - амплитуды полей. Таким образом, решения уравнений (1.4) для заданных условий имеют вид:
![]() . (1.7)
. (1.7)
Из (1.7) следует, в частности, что поля E и H в распространяющейся волне синфазны.
Освободиться от специального выбора системы координат можно, используя волновой вектор k = kn (n – единичный вектор, направленный по пути распространения радиоволны). Если r – радиус-вектор точки на поверхности фронта волны (рис. 1.1), то расстояние от т. О до фронта равно nr, и решения (1.3) можно представить в следующей форме:
![]() ,
, ![]() . (1.8)
. (1.8)

Справедливость (1.8) нетрудно проверить подстановкой в уравнения (1.3).
Выражения (1.8) описывают монохроматическую волну, т. е. волну, векторы напряженности которой меняются во времени по гармоническому закону с одной определенной частотой.
Найдем скорость распространения радиоволны как скорость перемещения ее фронта (рис.1.1). На такой поверхности фаза y = wt – kr = wt – knr = Const, следовательно,
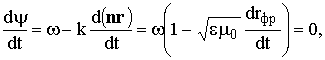 (1.9)
(1.9)
здесь rфр – проекция r на направление перемещения фронта волны.
Из (1.9) следует, что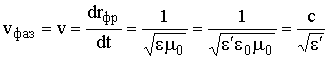 , где
, где 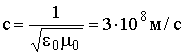 .
.
Определим ориентацию векторов E и H волны относительно направления распространения и между собой. Векторные операции в (1.2) можно выразить с помощью оператора 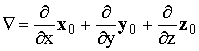 :
:
divE = ÑE, rotE = [Ñ, E], divH = ÑH, rotH = [Ñ, H].
Применим Ñ к экспоненте в (1.8). Поскольку kr = kxx + kyy + kyz, то Ñei(wt - kr) = eiwt Ñe - ikr = eiwt(-ik)e - ikr = -ik ei(wt - kr). Тогда два последних уравнения системы (1.2) можно записать как
divE = ÑE = -i(kE) = 0, divH = ÑH = -i(kH) =
Из (1.10) следует, что векторы E и H перпендикулярны волновому вектору k, а, следовательно, и направлению распространения волны.
Проанализируем теперь второе уравнение системы (1.2).
![]() . (1.11)
. (1.11)
Но ![]() , тогда после сокращений получим
, тогда после сокращений получим
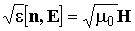 . (1.12)
. (1.12)
Из (1.12) следует, что векторы E и H взаимно перпендикулярны и образуют с направлением распространения правостороннюю тройку векторов.
Если, используя представление (1.8), взять модуль от обеих частей (1.12) и учесть, что ên ê= 1, êei… ê= 1, то
![]() ,
,
т. е. отношение величин амплитуд полей волны
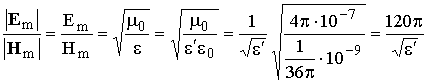 , (1.13)
, (1.13)
Пусть в декартовой системе координат плоская радиоволна распространяется вдоль оси Оx, а вектор E направлен вдоль Оz (рис. 1.2). Компоненты поля в тригонометрической форме будут иметь следующий вид:
 (1.14)
(1.14)
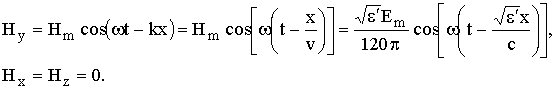 (1.15)
(1.15)

2.Распространение плоских радиоволн в однородной проводящей среде
В земных условиях к таким средам обычно относят ионосферу, водную толщу, почву. Здесь проводимость s ¹ 0, поэтому система уравнений Максвелла приобретает вид
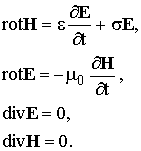 (2.1)
(2.1)
Полагая, что поле создается гармоническим током антенны, т. е. E ~ eiwt, имеем ![]() , откуда
, откуда ![]() . Подставив это выражение в первое уравнение системы (2.1), получаем:
. Подставив это выражение в первое уравнение системы (2.1), получаем:
![]() называется комплексной диэлектрической проницаемостью.
называется комплексной диэлектрической проницаемостью.
Уравнение (2.2) отличается от аналогичного из (1.2) лишь тем, что e заменяется на eк. Все остальные уравнения систем (2.1) и (1.2) совпадают, поэтому правомерно использовать результаты, полученные для идеального диэлектрика, заменив в них e' на относительную комплексную диэлектрическую проницаемость ![]()
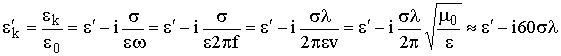 .
.
Представим ![]() в виде
в виде ![]() . Тогда из (1.7) следует
. Тогда из (1.7) следует
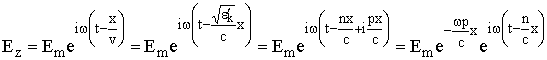 , (2.3)
, (2.3)
или в тригонометрической форме
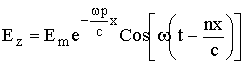 . (2.4)
. (2.4)
Из (2.4) следует, что в проводящей среде волна распространяется со скоростью ![]() , а амплитуда напряженности её поля с расстоянием уменьшается, т. е. имеет место затухание волны.
, а амплитуда напряженности её поля с расстоянием уменьшается, т. е. имеет место затухание волны.
Напряжённость магнитного поля радиоволны в проводящей среде
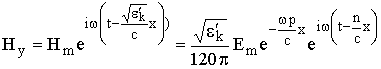 . (2.5)
. (2.5)
Используя в (2.5) представление 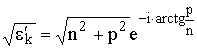 , получаем
, получаем
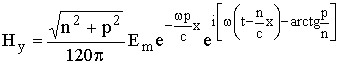 , (2.6)
, (2.6)
соответственно, в тригонометрической форме
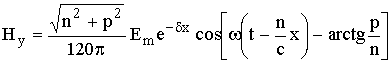 . (2.7)
. (2.7)
Таким образом, при распространении в проводящей среде:
1) волна остается поперечной;
2) по мере распространения волны в направлении x её амплитуда уменьшается по закону e - dx, где ![]() - коэффициент поглощения средой;
- коэффициент поглощения средой;
3) электрическая и магнитная составляющие поля радиоволны распространяются с одинаковой скоростью ![]() ;
;
4) в каждой точке пространства магнитное поле сдвинуто по фазе по отношению к электрическому полю на угол 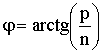 ;
;
5) амплитуда магнитного поля связана с амплитудой электрического поля соотношением 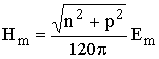 .
.
Рассматривая представления 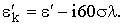 и
и 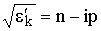 как систему двух уравнений, нетрудно получить, что
как систему двух уравнений, нетрудно получить, что
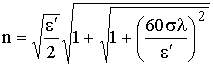 ,
, 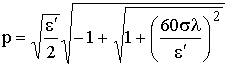 . (2.8)
. (2.8)
В некоторых случаях выражения (2.8) можно упростить /2/:
1) если e¢ >> 60sl (т. е. jпр << jсм), то n » ![]() , p »
, p » ![]() ; (2.9)
; (2.9)
2) если e¢ << 60sl (т. е. jпр >> jсм), то n » p » ![]() . (2.10)
. (2.10)
3. Принцип Гюйгенса и зоны Френеля
Определим область пространства, в которой распространяется основная часть радиоволны, формирующая сигнал в точке приёма. Размер и конфигурация такой области определяются принципом Гюйгенса - Френеля, согласно которому каждая точка фронта распространяющейся волны, созданной каким-то первичным источником А, сама является источником новой сферической волны (рис. 3.1).
 Полное поле в точке приема В может быть определено либо непосредственно как поле первичных источников, либо путем суммирования элементарных полей, создаваемых вторичными источниками, распределенными по замкнутой поверхности, охватывающей первичные источники. В теории такой вторичный источник называется элементарным источником Гюйгенса, и диаграмма направленности его излучения имеет форму кардиоиды (F(j) = 0,5 (1 + Cosj)). Рассмотрим построение, предложенное Френелем (рис. 3.2). Пусть в т. А помещён излучатель, а в т. В – приёмная антенна. Источник создаёт сферическую волну, т. е. волну, поверхностью равных фаз которой является сфера с центром в т. A. Построим конические поверхности с вершиной в т. В и осью АВ такие, чтобы образующие конусов отличались между собой на величину
Полное поле в точке приема В может быть определено либо непосредственно как поле первичных источников, либо путем суммирования элементарных полей, создаваемых вторичными источниками, распределенными по замкнутой поверхности, охватывающей первичные источники. В теории такой вторичный источник называется элементарным источником Гюйгенса, и диаграмма направленности его излучения имеет форму кардиоиды (F(j) = 0,5 (1 + Cosj)). Рассмотрим построение, предложенное Френелем (рис. 3.2). Пусть в т. А помещён излучатель, а в т. В – приёмная антенна. Источник создаёт сферическую волну, т. е. волну, поверхностью равных фаз которой является сфера с центром в т. A. Построим конические поверхности с вершиной в т. В и осью АВ такие, чтобы образующие конусов отличались между собой на величину ![]() (m = 1, 2,…). Тогда должны выполняться следующие равенства:
(m = 1, 2,…). Тогда должны выполняться следующие равенства:
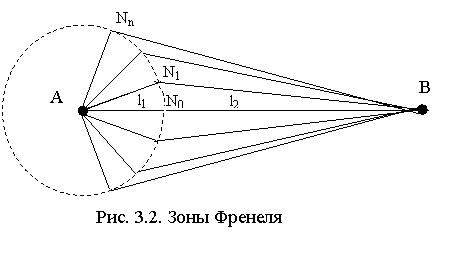 |
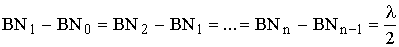 . (3.1)
. (3.1)
Пересечение конусов с фронтом волны образует на сферической поверхности семейство коаксиальных окружностей. Участки поверхности сферы, заключённые между смежными окружностями, называются зонами Френеля. Первая, или главная, зона Френеля – часть сферы, ограниченная окружностью N1, зоны высших порядков представляют собой кольцевые области. Из (3.1) следует, что фазы радиоволн, излучаемых виртуальными источниками смежных зон, отличаются в среднем на p.
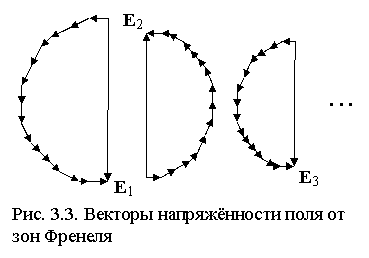 Разобьём каждую зону Френеля на большое количество колец конечной ширины и просуммируем векторы напряжённости поля в точке приёма от каждого кольца (рис. 3.3). Пусть Ei - результирующая амплитуда напряжённости поля волны в т. приёма от i-й зоны Френеля. Векторы от соседних зон направлены в проти-воположные стороны, т. к. их фазы отличаются на p. С ростом i амплитуда Ei будет убывать как за счёт удаления вторичных источников от т. приёма, так и потому, что направление максимума их излучения всё более отклоняется от направления на точку приёма. Результирующую амплитуду волн от вторичных источников всех зон Френеля можно представить в виде знакопеременного сходящегося ряда
Разобьём каждую зону Френеля на большое количество колец конечной ширины и просуммируем векторы напряжённости поля в точке приёма от каждого кольца (рис. 3.3). Пусть Ei - результирующая амплитуда напряжённости поля волны в т. приёма от i-й зоны Френеля. Векторы от соседних зон направлены в проти-воположные стороны, т. к. их фазы отличаются на p. С ростом i амплитуда Ei будет убывать как за счёт удаления вторичных источников от т. приёма, так и потому, что направление максимума их излучения всё более отклоняется от направления на точку приёма. Результирующую амплитуду волн от вторичных источников всех зон Френеля можно представить в виде знакопеременного сходящегося ряда
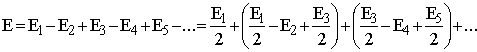 (3.2)
(3.2)
Обычно расстояние между передающей и приёмной антеннами значительно превышает длину волны, т. е.
l1 + l2 >> l. (3.3)
Тогда амплитуды Ei от соседних зон мало отличаются друг от друга и можно считать, что ![]() , т. е. выражения в скобках в (3.2) близки к нулю. Таким образом, в результате взаимной компенсации сигналов от соседних зон высших порядков результирующая амплитуда поля от всех зон Френеля
, т. е. выражения в скобках в (3.2) близки к нулю. Таким образом, в результате взаимной компенсации сигналов от соседних зон высших порядков результирующая амплитуда поля от всех зон Френеля ![]() , т. е. эквивалентна излучению половины первой зоны Френеля (реально полной компенсации соседних зон не происходит, поэтому более точно
, т. е. эквивалентна излучению половины первой зоны Френеля (реально полной компенсации соседних зон не происходит, поэтому более точно ![]() ). В первом приближении полагают, что поверхность первой зоны Френеля и есть область пространства, ответственная за создание сигнала в точке приёма.
). В первом приближении полагают, что поверхность первой зоны Френеля и есть область пространства, ответственная за создание сигнала в точке приёма.
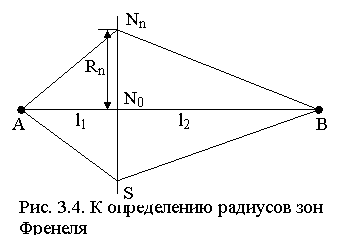 Зоны Френеля могут быть построены на поверхности произвольной формы. Найдём радиус n-й зоны Френеля на плоскости S, перпендикулярной направлению распространения, в предположении, что распространяется плоская радиоволна. Согласно обозначениям рис. 3.4,
Зоны Френеля могут быть построены на поверхности произвольной формы. Найдём радиус n-й зоны Френеля на плоскости S, перпендикулярной направлению распространения, в предположении, что распространяется плоская радиоволна. Согласно обозначениям рис. 3.4,
![]() . (3.4)
. (3.4)
Если выполняется условие l1, l2 >> l, то
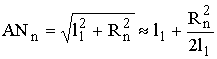 ,
, 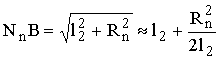 . (3.5)
. (3.5)
Подставив выражения (3.5) в (3.4), нетрудно получить
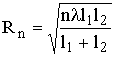 . (3.6)
. (3.6)
Зафиксируем на плоскости S, перпендикулярной трассе AB, точки образующей n-й зоны Френеля и будем перемещать S вдоль трассы (рис. 3.5). Из (3.4) следует, что в этом случае выполняется равенство
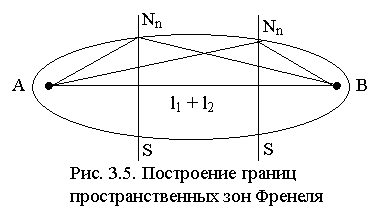
![]() . (3.8)
. (3.8)
Математически (3.8) есть уравнение эллипса, следовательно, границы зон Френеля в пространстве представляют собой поверхности эллипсоидов вращения с фокусами в точках А и В. Области пространства между двумя соседними эллипсоидами называют пространственными зонами Френеля. Максимума радиус сечения эллипсоида плоскостью S достигает при l1 = l2 = AB/2:
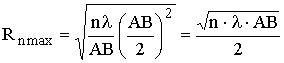 . (3.9)
. (3.9)
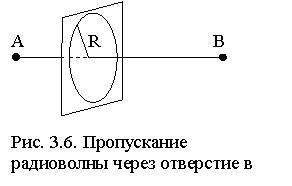 Экспериментально существование зон Френеля подтверждается, например, изменчивостью в точке приёма B напряжённости поля, создаваемого источником в т. A, при изменении радиуса R отверстия в условно бесконечном экране (рис. 3.6). В полном соответствии с принципом Гюйгенса сложение сигналов от неперекрытых еще зон Френеля приводит к колебаниям сигнала. Другой пример приведён в разделе 7.
Экспериментально существование зон Френеля подтверждается, например, изменчивостью в точке приёма B напряжённости поля, создаваемого источником в т. A, при изменении радиуса R отверстия в условно бесконечном экране (рис. 3.6). В полном соответствии с принципом Гюйгенса сложение сигналов от неперекрытых еще зон Френеля приводит к колебаниям сигнала. Другой пример приведён в разделе 7.
4. Отражение радиоволн от поверхности плоской Земли
Пусть приемная антенна установлена вблизи поверхности Земли. Влияние земной поверхности на распространение радиоволн наиболее просто учесть, когда антенна поднята на высоту порядка нескольких длин волн.
Если радиоволна достигает земной поверхности на значительном по сравнению с l расстоянии от излучателя, то участок фронта волны вблизи приёмной антенны можно аппроксимировать плоскостью. При небольшой протяженности радиолинии земную поверхность можно считать плоской в метровом диапазоне для трасс длиной докм, в декаметровом - до нескольких десятков км, на СВ и ДВ - до нескольких сотен км.
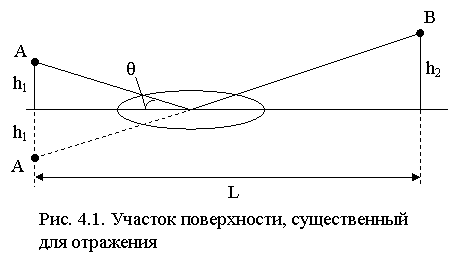 На границе раздела "земля-воздух" происходит отражение радиоволны (рис. 4.1), так что поле в т. приема B является резуль-татом интерфе-ренции поля пе-рвичной волны, пришедшей из т. излучения A, и отраженной волны. Используя метод зеркальных отображений, можно заменить влияние Земли полем источника, расположенного в точке A' зеркального отображения реального излучателя A, умноженным на коэффициент отражения R (для идеально проводящей поверхности |R| = 1). Рассматривая A'B как реальную трассу, выделим пространственные зоны Френеля, существенные для распространения. Пересечение 6 ¸ 8 первых зон с земной поверхностью образует конфокальные эллипсы, поверхность которых можно считать зоной, существенной для отражения. Если этот участок достаточно плоский, ровный и однородный, то и всю поверхность раздела можно рассматривать как ровную, однородную и безграничную.
На границе раздела "земля-воздух" происходит отражение радиоволны (рис. 4.1), так что поле в т. приема B является резуль-татом интерфе-ренции поля пе-рвичной волны, пришедшей из т. излучения A, и отраженной волны. Используя метод зеркальных отображений, можно заменить влияние Земли полем источника, расположенного в точке A' зеркального отображения реального излучателя A, умноженным на коэффициент отражения R (для идеально проводящей поверхности |R| = 1). Рассматривая A'B как реальную трассу, выделим пространственные зоны Френеля, существенные для распространения. Пересечение 6 ¸ 8 первых зон с земной поверхностью образует конфокальные эллипсы, поверхность которых можно считать зоной, существенной для отражения. Если этот участок достаточно плоский, ровный и однородный, то и всю поверхность раздела можно рассматривать как ровную, однородную и безграничную.
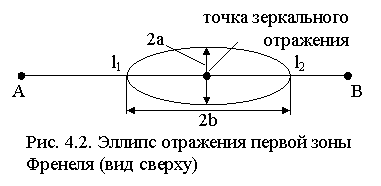 Размеры полуосей a и b эллипса, образованного первой зоной Френеля при отражении (рис. 4.2), определяются следующими формулами /2/:
Размеры полуосей a и b эллипса, образованного первой зоной Френеля при отражении (рис. 4.2), определяются следующими формулами /2/:
 - малая,
- малая, 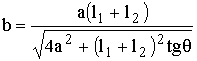 - большая полуось.
- большая полуось.
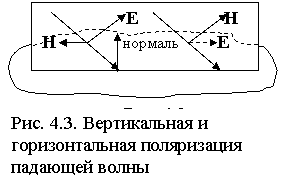 Плоскость падения - плоскость, проходящая через направление паде-ния волны и нормаль к граничной поверхности (к поверхности раздела двух сред) в точке падения. Если вектор поля E лежит в плоскости падения, то падающая волна называется волной с вертикальной поляризацией (рис.4.3). Если E перпендикулярен плоскости падения, то волна считается поляризованной горизонтально. В случае произвольной ориентации вектора E его можно разложить на вертикальную и горизонтальную составляющие EВ и EГ.
Плоскость падения - плоскость, проходящая через направление паде-ния волны и нормаль к граничной поверхности (к поверхности раздела двух сред) в точке падения. Если вектор поля E лежит в плоскости падения, то падающая волна называется волной с вертикальной поляризацией (рис.4.3). Если E перпендикулярен плоскости падения, то волна считается поляризованной горизонтально. В случае произвольной ориентации вектора E его можно разложить на вертикальную и горизонтальную составляющие EВ и EГ.
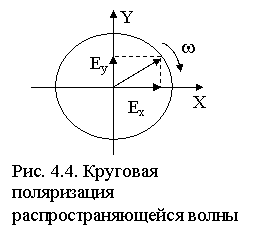
Когда вектор E при распространении волны не меняет своей ориентации в пространстве (т. е. описывает прямую по фронту волны), такую волну называют линейно поляризованной. Если вектор E распространяющейся волны, оставаясь постоянным по величине, меняет свое направление в пространстве так, что его конец описывает окружность (рис. 4.4), говорят о круговой поляризации волны. Такую волну можно представить как суперпозицию двух линейно поляризованных волн
Ex = Em cos(wt - kr), Ey = Em cos(wt - kr - p/2)
с равными амплитудами и фазами, сдвинутыми на p/2.
Если вектор E меняется и во времени и в пространстве так, что его конец в общем случае описывает эллипс, то такую волну называют эллиптически поляризованной. Её тоже можно представить как суперпозицию двух линейно поляризованных волн
Ex = Exm cos(wt - kr), Ey = Eym cos(wt - kr - j), где Exm ¹ Eym и j ¹ 0.
5. Отражение плоских радиоволн на границе раздела двух сред
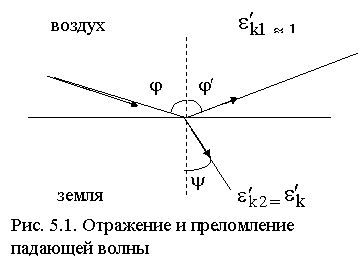
При падении радиолуча на поверхность раздела сред может происходить как его отражение, так и преломле-ние. Пусть направление па-дающей волны составляет угол j с нормалью к поверхности, направление от-раженной волны - угол j' и направление преломленной волны - угол y (рис. 5.1). Из электродинамической теории известна связь между этими углами:
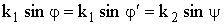 , (5.1)
, (5.1)
откуда сразу имеем условие отражения j = j'. Из определения волнового числа ![]() , полагая для воздуха
, полагая для воздуха ![]() = 1 и для земли
= 1 и для земли ![]() =
=![]() , запишем условие преломления
, запишем условие преломления
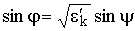 . (5.2)
. (5.2)
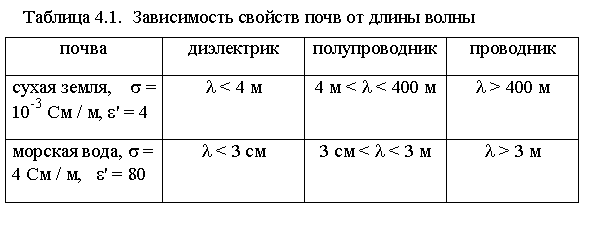 |
В зависимости от длины волны земная поверхность может иметь свойства диэлектрика (если e' >> 60sl, т. е.
Параметры s и e' почвы зависят и от частоты распространяющейся волны, однако эта зависимость проявляется лишь для дециметровых и более коротких волн (т. е. при f > 300 МГц). С ростом f, вплоть до частоты резонанса молекул воды (1,5 ¸ 6)×104 МГц, e' уменьшается, а s возрастает.
5.1. Коэффициент отражения вертикально поляризованной волны
Пусть на поверхность раздела падает гармоническая волна Eпад = Em пад coswt (или Eпад = Em пад eiwt). На границе раздела сред должны выполняться условия равенства тангенциальных составляющих векторов E и H E1t = E2t и (при отсутствии поверхностных токов) H1t = H2t, на основании чего для вертикально поляризованной волны можно составить систему двух уравнений:
Em пад cosj - Em отр cosj = Em пр cosy, (5.3)
Hm пад + Hm отр = Hm пр. (5.4)
Коэффициент отражения волны R определяется как отношение амплитуд 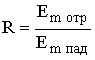 . Пусть свойства земли близки к идеальному диэлектрику. Тогда из (1.13) и (5.4) следует
. Пусть свойства земли близки к идеальному диэлектрику. Тогда из (1.13) и (5.4) следует 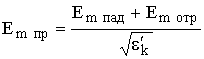 . Подставим это выражение в (5.3), поделим всё на Em пад. Перейдя к углу скольжения
. Подставим это выражение в (5.3), поделим всё на Em пад. Перейдя к углу скольжения 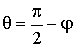 , с помощью (5.2) исключим угол y:
, с помощью (5.2) исключим угол y: 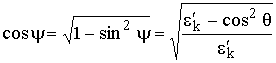 и получим
и получим
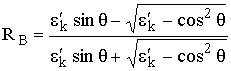 . (5.5)
. (5.5)
Если проводимость почвы s ¹ 0, то e¢k является комплексной величиной, комплексно и выражение (5.5), поэтому RB можно представить в виде
 , (5.6)
, (5.6)
т. е. при взаимодействии радиоволны с проводящей поверхностью появляется сдвиг фаз между падающей и отраженной волнами на угол bВ.
Проанализируем выражение (5.5) для различных свойств земной поверхности:
а) 60sl << e' , e'k » e', т. е. почва близка к идеальному диэлектрику. Тогда коэффициент отражения
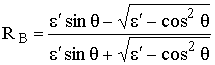 (5.7)
(5.7)
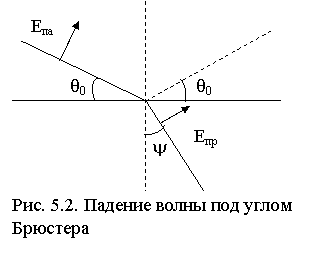 является вещественной величиной. При малых q e' sinq ® 0 и RВ ® -1 (отрицательность RВ интерпретируется как изменение фазы R на p). При возрастании q достигаем угла
является вещественной величиной. При малых q e' sinq ® 0 и RВ ® -1 (отрицательность RВ интерпретируется как изменение фазы R на p). При возрастании q достигаем угла 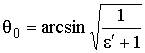 , называемого углом Брюстера, при котором числи, а следовательно, и RВ, равен 0. При падении волны под таким углом отражение отсутствует, и вся энергия падающей волны переходит в энергию преломленной волны (рис. 5.2).
, называемого углом Брюстера, при котором числи, а следовательно, и RВ, равен 0. При падении волны под таким углом отражение отсутствует, и вся энергия падающей волны переходит в энергию преломленной волны (рис. 5.2).
* Объяснение эффекта полного преломления. При прохождении волны в земной поверхности находящиеся в ней заряды колеблются в направлении вектора волны E, становясь по сути дипольными излучателями. При q = q0 ориентация таких диполей совпадает с направлением отражения падающей волны. Но диполи не излучают вдоль своей оси, следовательно, не будет и отражённой волны.
*
В интервале углов q0 £ q £ p / 2 коэффициент RВ растёт от 0 до значения 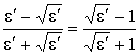 > 0, это означает, что для указанных углов скольжения фаза при отражении не меняется.
> 0, это означает, что для указанных углов скольжения фаза при отражении не меняется.
б) 60sl >> e' , т. е. e'k » i60sl, и почву можно рассматривать как проводник. В этом случае |RВ| = 1, поскольку по законам электродинамики Em пр = 0, следовательно, должно происходить полное отражение. Тогда из (5.3) следует, что Em пад = Em отр, т. е. фаза волны при отражении не меняется.
в) 60sl » e' - случай полупроводящей поверхности. В целом, ½RВ½и bВ меняются как и для случая а), только ½RВ½ в нуль не обращается, а имеет минимум при некотором угле q0.
5.2. Коэффициент отражения горизонтально поляризованной волны
Исходя из равенств тангенциальных составляющих полей, получаем следующую исходную систему уравнений:
Em пад + Em отр = Em пр, (5.8)
Hm пад cosj - Hm отр cosj = Hm пр cosy, (5.9)
откуда, выполняя преобразования аналогично предыдущему разделу, определяем коэффициент отражения RГ
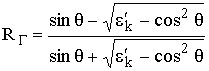 . (5.10)
. (5.10)
Случаи различных свойств отражающей поверхности:
а) почва – диэлектрик. Тогда коэффициент отражения
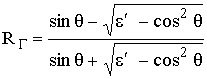
вещественен, для всех углов q RГ < 0, следовательно, при любых q сдвиг фаз bГ равен p. При q = 0 RГ = -1, с ростом q ½RГ½ плавно убывает, и при ![]() ½RГ½=
½RГ½= 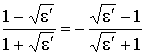 , что равно величине ½RВ½для того же угла.
, что равно величине ½RВ½для того же угла.
б) почва - проводник. В этом случае для любых углов q RГ » -1, т. е. вся падающая энергия отражается, фаза меняется на p, что следует из (5.8): если Em пр = 0, то должно быть Em пад = - Em отр.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 |