в) почва – полупроводник. В этом случае RГ - комплексный.

Из полученных выше результатов следует, что |RГ| = |RВ| при q = 0 и . Для всех других углов скольжения |RГ| > |RВ|, что является, в частности, причиной преимущественного применения в радиолокации, телевидении, УКВ волн с горизонтальной поляризацией.

6. Влияние шероховатости отражающей поверхности

Выражения для коэффициентов RВ и RГ были получены в предположении ров­ной отражающей поверхности, по крайней мере, в пределах области формирова­ния отраженной волны. Однако, реальная земная поверхность никогда не бывает абсолютно гладкой. Даже равнинная местность покрыта большим числом хаотически расположенных неровностей. Если не­большие неровности в среднем расположены равномерно, такую поверхность называют шероховатой (для УКВ это, например, взволнованная поверхность моря; для СВ и ДВ - небольшие холмы и здания). Отражение от неровной поверхности является рассеянным, поэтому напряжен­ность поля в направлении зеркального отражения будет меньше, чем для гладкой поверхности. Это ослабление можно учесть с помощью эффективного коэффициента отражения Rэфф, расчет коего достаточно сложен. Качественно «гладкость» поверхности можно оценить с помощью критерия Релея.

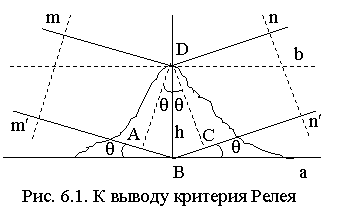
6.1. Критерий Релея. Пусть плоская волна отражается от неровной поверхности с максимальным разме­ром неоднородностей h (рис. 6.1). Часть мощности падающей волны отразится на верхнем уровне (b), часть - на нижнем (a). Плоскость m - m¢ является плоскостью равных фаз падающей волны. Определим фазовые отношения на плоскости, перпендикулярной направлению отражения волны n - n¢. Наибольшая разность фаз Dj будет между волнами, отражен­ными в т. т. D и B. Разность хода лучей mDn и m¢Bn¢ Dr = ABC = 2AB = 2hsinq, отсюда 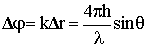. Считается, что отражающую поверхность можно считать гладкой, если допустимые фазовые искажения на плоскости n – n¢

,

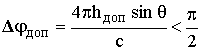отсюда, собственно, критерий Релея

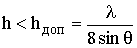. (6.1)

Из (6.1) следует, что чем более полога траектория и чем больше l, тем слабее возмущающее действие неровностей. Например, для волны длиной l = 10 см при угле скольжения 50 hдоп = 14 см, а при уменьше­нии q до 0,50 hдоп возрастает до 1,4 м.

Критерий Релея носит приближенный характер, поскольку не учитывает форму неровностей, вид поляризации и т. п. Однако, качественно он правильно оценивает степень шероховатости отражающих поверхностей.

2. Закон Ламберта. Если отражающая поверхность является матовой, т. е. покрыта неоднородностями с h > hдоп по Рэлею, наблюдается диффузное, или рассеянное, отражение, при котором "яркость" отражающей поверхности во всех направлениях при равных углах скольжения примерно одинакова (рис. 6.2). Зависимость интенсивности J рас­сеянного сигнала от угла j описывается законом Ламберта

J = J0 cosj (6.2)

(J0 - значение J при j = 0), который был установлен в результате экспериментальных исследований яркости светящихся поверхностей. Закон Ламберта выполняется при наличии следующих условий:

1) концентрация неровностей постоянна на всей отражающей поверхности,

2) отражающая поверхность в среднем не отклоняется от плоскости,

3) неодородности не создают теневых областей, что справедливо, если неоднородностей имеют разме­ры £ l.

3. Отражающая поверхность Земли не бывает идеально гладкой или только шероховатой, поэтому отражение радиоволн зачастую носит полурассеянный характер с максимумом в направлении зеркального отражения (рис. 6.3). Чем короче волна, тем вероятнее выполнение условий, при которых отражение близко к диффузному. Это в первую очередь относит­ся к см и более коротким волнам.

7. Распространение радиоволн при наличии экранирующих препятствий

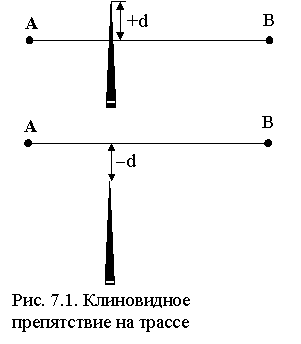Оценим влияние экранирующего препятствия в предположении, что препятствие имеет форму непрозрачного клина. Такая аппроксимация при­меняется, если размеры препятствия (вершины клина) вдоль трассы << размера поперечного се­чения эллипсоида, существен­ного для распространения, а размеры поперек трассы >> этого размера. Пусть такое препятствие характеризуется высотой экранирования d, равной воз­вышению гребня клина над линией прямой видимости, соединяющей точки излучения A и приема B (рис. 7.1).

Если пренебречь физическими свойствами клина (s, m, e), то можно свести задачу к оптической дифракции, а именно, поле E в точке приёма определяется формулой E = F×E0, в которой E0 - поле в свободном пространстве, а F - дифракционный множитель

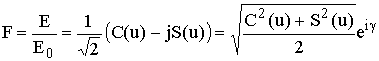. (7.1)

Здесь 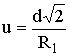(R1 - радиус первой зоны Френеля), 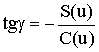, 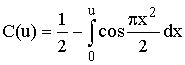и 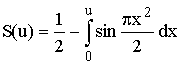- интегралы Френеля.

Изображение зависимостей C(u) и S(u) от u представляет собой спираль Корню. Изменчивость множителя F в зависимости от u (по сути, от высоты экрана, вы­раженной в зонах Френеля) представлена на рис. 7.2: F флуктуирует около 1 при d < 0, равен 0,5 при d = 0 и плавно понижается до 0 при d > 0.

Полученные результаты позволяют приближённо рассчитывать напряжённость поля на трассах, проходящих над остроконечными холмами и горными кряжами. Отметим, что независимо от формы препятствия с ростом длины волны дифракционные потери уменьшаются.

7.1. Эффект "усиления препятствием"

Наблюдается обычно на трассах УКВ протяжённостью 100 ¸ 150 км, проходящих через горные кряжи высотой 1 ¸ 2 км, и заключается в том, что напряжённость электрического поля радиоволны при некотором удалении от препятствия может оказаться большей, чем на таком же расстоянии от передающей антенны на трассе без препятствий. Теоретически эффект усиления радиосигнала вытекает из теоремы Фейнберга: задача о поле излучателя над идеально проводящей землей с выступом эквивалентна задаче о поле такого же излучателя и его зеркального изображения в свободном пространстве при наличии препятствия, имеющего форму выступа, состыкованного со своим зеркальным изображением.

Пусть на трассе имеется клиновидное препятствие (рис. 7.3), с вершины H которого видны как передающая антенна А, так и приемная В. В точку H приходят два луча: прямой (AH) и отраженный от земной поверхности (ACH). Они возбуждают вершину препятствия, в результате чего в точке В должна наблюдаться суперпозиция 4-х лучей: двух, возбужденных прямым лучом, и двух, воз­бужденных отраженным лучом. Обозначим длины путей распространения

r1 = AH + HB, r2 = AH¢ + H¢B, r3 = A¢H + HB, r4 = A¢H¢ + H¢B.

Тогда поле в точке приёма B

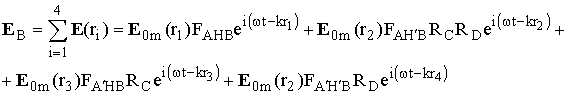
и

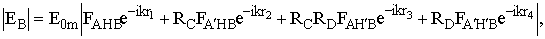(7.2)

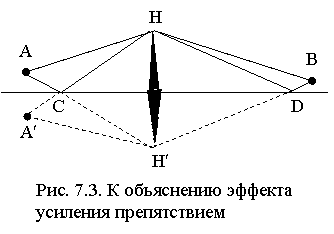где RC и RD - коэффициенты отражения лучей от почвы в точках C и D. Практический интерес представляют пологие трассы, когда RC » RD » -1 и дифракционые множители F мало отличаются друг от друга. В этом случае из (7.2) следует, что |EB| £ 4E0m, т. е. поле радиоволны в точке приема В, находящейся за препятствием, не может превосходить 4-кратного значения поля при распространении в свободном пространстве.

Эффект усиления препятствием возможен, если потери при огибании пре­пятствия не слишком велики. Обычно абсолютное усиление поля невелико, одна­ко если длина трассы значительно превышает расстояние прямой видимости, так что точка приема при отсутствии препятствия находится в глубокой тени за горизонтом, эф­фект усиления может быть значительным. Практика показывает, что на таких трассах препятствие, выполняющее роль пассивного ретранслятора, способно увеличить напряжённость поля радиоволны на 60 ¸ 80 дБ по сравнению с дифракционным.

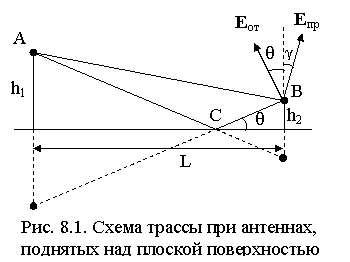
8. Распространение радиоволн при антеннах, поднятых над плоской Землей

Поднятой считается антенна, питаемая неизлучающим фидером и расположенная на расстоянии не менее нескольких l от земной поверх-ности. Пусть в точке А свободного пространства (e' = 1, m = m0, s = 0) расположен точечный изотропный излучатель мощностью P. Средняя за период плотность потока мощности излученной волны определяется величиной вектора Пойнтин­га П = [E, H]. В вол­новой зоне (kr >> 1) можно полагать, что векторы E и H перпендикулярны направлению распространения, следовательно, . Рассматривая небольшой участок фронта волны как плоский, имеем 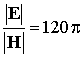. Таким образом, на расстоянии r от излучателя 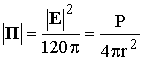[Вт / м2], откуда

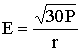[В / м]. (8.1)

Реальные антенны обладают направленными свойствами. Степень концентрации антенной энергии радиоволны в определённом направлении характеризуется коэффициентом усиления антенны G, показывающим, во сколько раз плотность мощности, создаваемая направленной антенной в данном направлении на расстоянии r, превышает плотность мощности, создаваемую изотропным излучателем на том же расстоянии при условии, что излучается одинаковая мощность. Напряженность поля, создаваемого направлен­ной антенной,

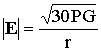[В / м] = 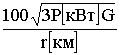[мВ / м]. (8.2)

Выражение (8.2) определяет действующее, или среднее за период (< >) значение напряженности поля гармонической волны. Так как

,

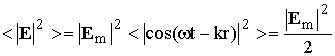то амплитудное значение напряженности поля

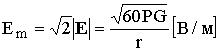. (8.3)

Пусть в точку B (рис. 8.1) приходят как прямой луч с напряжённостью Eпр, так и отраженный от поверхности луч с Eотр. Для плоской волны

Eпр = , Eотр = ,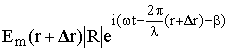

где r = AB, r + Dr = AC + CB, R – коэффициент отражения в точке C, b определяет возможное изменение фазы волны при отражении.

8.1. Горизонтальная поляризация падающей волны

В этом случае напряжённость поля в точке приема EB = Eпр + Eотр, т. е.

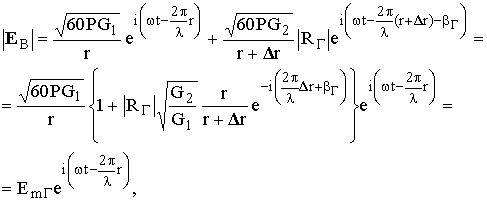(8.4)

здесь G1, G2 – коэффициенты усиления передающей антенны в направлении соответственно на точку приёма и на точку отражения, EmГ – комплексная амплитуда принимаемой радиоволны

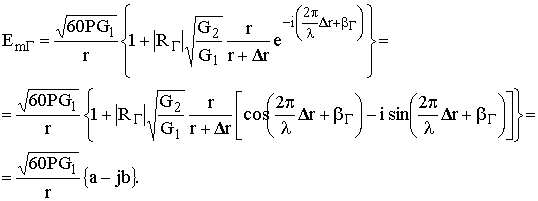(8.5)

Следовательно,

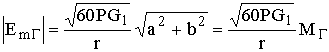. (8.6)

Параметр MГ

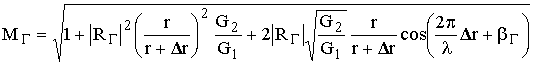(8.7)

называется интерференционным множителем.

Действующее значение EГ напряжённости поля в точке приема

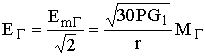. (8.8)

8.2. Вертикальная поляризация падающей волны

В точке приема B будет иметь место суперпозиция полей с результирующей напряженностью (рис. 8.1)

EB = Eпрcosg + Eотрcosq, (8.9)

где .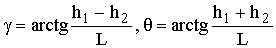

После выполнения преобразований, аналогичных предыдущему разделу, можно по­лучить

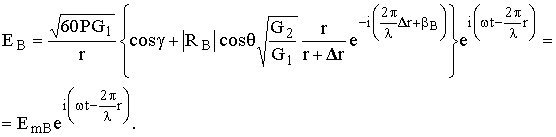
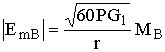, (8.10)

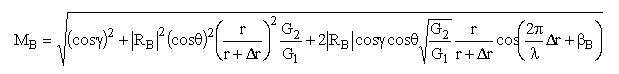здесь MВ – интерференционный множитель,

(8.11).

Согласно рис. 8.1, .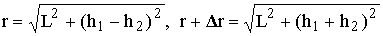

Обычно можно полагать, что h1, h2 << L, тогда

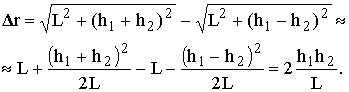(8.12)

Для пологих трасс, когда углы g и q малы, в выражениях (8.7), (8.11) допустимы следующие замены:

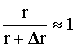, r » L, G1 » G2 » G, cosg »1, cosq »1, |RГ| »1, |RВ| »1, bГ »p, bВ »p.

Тогда получаем, что

EmВ, EmГ » .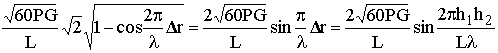

При h1, h2 << L аргумент функции sin является малой величиной, и можно полагать, что sinx » x. Следовательно,

EmВ, Em Г » 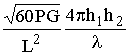. (8.13)

Выражение (8.13) называют формулой Введенского. Критерием её применимости считается выполнение условия .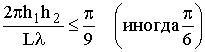

Анализ формулы Введенского показывает, что

1) при малых углах скольжения поле E убывает с расстоянием ~ r2. Столь быстрое убывание поля над поверхностью по сравнению с распространением в свободном пространстве (8.1) является следствием примерного равенства амплитуд Eпр и Eотр и сдвига фазы при отражении ~ на p;

2) формула даёт правильные результаты, если h1 и h2 > 0, т. е. если антенны подняты над поверхностью;

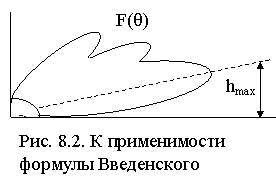
3) E должна расти с увеличением h1 и h2. На практике считается, что формула Введенского применима до высоты подъёма точки приёма hmax, соответствующей первому максимуму диаграммы направленности передающей антенны (рис. 8.2);

4) в городских условиях можно оценить средний уров­ень E по формуле Введенского, вводя в нее множитель, равный 0,2 ¸ 0,4, и отсчитывая высоту антенн от среднего уровня крыш.

9. Поверхностное распространение радиоволн

Интерференционные формулы, полученные для поднятых антенн, не применимы в случае радиоволн, распространяющихся вдоль земной поверхности. В самом деле, если углы скольжения равны 0, то для любого вида поляризации коэффициент отражения R = -1 независимо от свойств поверхности. Следовательно, поле в точке приёма

E = Eпр + Eотр = Eпр + EпрR = Eпр(= 0.

Однако известно, что поле E = 0, только если проводимость поверхности s ® ¥.

Задачу распространения радиоволн в слу­чае, когда и передающая, и приемная антенны расположены на земной поверхности, можно решить, составив системы уравнений Максвелла для воздуха и земли и найдя их общее решение при следующих граничных условиях на поверхности:

1) равенство горизонтальных составляющих напряжённости полей

E1Г = E2Г, H1Г = H2Г ; (9.1)

2) равенство вертикальных составляющих индукций:

D1В = D2В (если нет поверхностных зарядов), или e'k1E1В= e'k2E2В,

(9.2)

B1В = B2В, или m'1H1В= m'2H2В.

При размещении антенн непосредственно на земной поверхности предпочтительнее использовать антенны, излучающие вертикально поляризованную волну, что следует из следующего анализа. В случае идеально проводящей поверхности (к этому случаю близко, например, распространение ДВ над морской поверхностью) волна распространяется только в верхнем полупространстве, следовательно, плотность энергии радиоволны, излученной находящимся на такой поверхности вертикальным диполем, вблизи поверхности будет в два раза, а напряжённость поля в раз больше по сравнению с распространением в свободном пространстве (8.3):

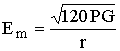, (9.3)

при этом вектор П направлен вдоль земной поверхности.

Если излучателем является горизонтальный диполь, то из (9.1) при E2Г = 0 следует, что напряжённость поля E вблизи идеально проводящей поверхности равна нулю. В случае полупроводящей поверхности напряжённость поля, создаваемая горизонтальным вибратором, уже не равна нулю, однако значительно меньше поля вертикального диполя.

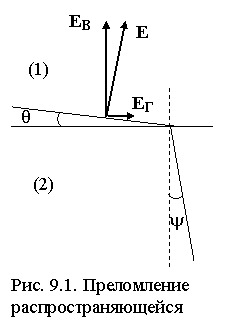
При распространении радиоволны над полупроводящей средой часть её энергии проникает вглубь (отклоняется) (рис. 9.1), следовательно, появляется вертикальная составляющая вектора Пойнтинга. Таким образом, вектор E волны, излученной вертикальным диполем, уже не перпендикулярен поверхности, т. е. появляется горизонтальная составляющая E1Г. Найдём соотношение между вертикальной и горизонтальной составляющими поля волны. Если электромагнитная волна проходит из воздуха в землю, согласно закону преломления,

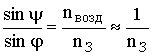. (9.4)

Обычно для земной поверхности 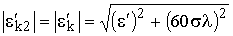>> 1. Тогда и 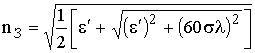>> 1, следовательно,

.

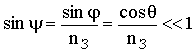Отсюда следует, что даже при очень малых углах скольжения q y ® 0, т. е. преломленная волна будет распространяться в земной толще почти перпендикулярно её поверхности. По сравнению с длиной волны l в свободном пространстве в среде lср = l / nср = l / nЗ << l, т. е. волна, проникающая вглубь земли, значительно укорачивается. На протяжении расстояния lср поле волны над поверхностью меняется мало, и распространяющуюся в земной толще волну можно считать плоской. Для такой волны выполняется уже известное нам соотношение между горизонтальными E - и H-компонен­тами

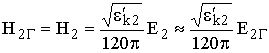. (9.5)

Из (9.5) и (9.1) следует, что вблизи поверхности

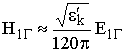, (9.6)

т. е. соотношение между EГ и HГ в воздухе определяется свойствами этой поверхности. Выражение (9.6) называют приближённым граничным условием Леонтовича.

Для плоской волны в нейтральной атмосфере

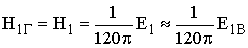. (9.7)

Подставляя (9.7) в (9.6), получаем

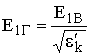. (9.8)

Тогда из (9.1) следует, что

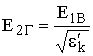. (9.9)

Из граничных условий (9.2) для вертикальной составляющей поля при e'k1 = 1 имеем E1В = e'k2E2В, следовательно,

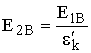. (9.10)

Соотношения (9.9) и (9.10) определяют составляющие поля E в земле через вертикальную компоненту поля в воздухе. Из них же следует, что

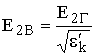. (9.11)

Полученные выше результаты позволяют сделать следующие выводы:

1) можно вести прием волны с исходной вертикальной поляризацией на горизонтальный провод, натянутый в направлении распространения, что конструктивно часто более удобно, чем ставить вертикальную антенну;

2) если |e'k| >> 1, то E2Г > > E2В, следовательно, под земной поверхностью предпочтительнее вести приём на горизонтальную антенну.

10. Напряжённость поля радиоволны, распространяющейся вдоль земной поверхности

Пусть в точке передачи на поверхности расположен вертикальный диполь. При распространении радиоволны вдоль неидеально проводящей поверхности часть энергии проникает в толщу Земли и там теряется. Уменьшение напряженности поля по сравнению с распространением над идеально проводящей поверхностью (9.3) учитывается введением множителя ослабления W, являющегося в общем случае комплексной функцией W = W(r, e, m, s, l), причём ½W½£ 1. Таким образом, амплитуда поля радиоволны над полупроводящей поверхностью определяется выражением

, (10.1)

получившим название «формула Шулейкина - Ван-дер-Поля».

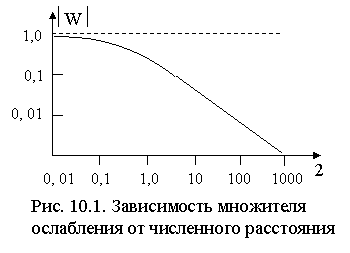Значения W, получаемые путём решения уравнений электродинамики, обычно представляют в виде графиков зависимости ½W(r)½ (рис. 10.1), где параметр

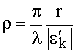(10.2)

называется ­численным расстоянием. Для аналитического представления зависимости используют аппроксимирующую формулу

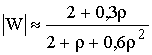. (10.3)

Согласно (10.3), при небольших r |W| » 1, при r >> 1 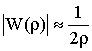. Тогда из (10.1) следует, что при малых длинах трасс E ~ ; а при больших значениях r |W| ~ , следовательно, E ~ . Согласно (10.2), увеличение l, s, e' уменьшает r, что ведёт к росту |W|, а значит, и поля в точке приёма.

Заметим, что приведенные выше зависимости |W| справедливы лишь до некоторого rmax, зависящего, в основном, от длины волны l (табл. 10.1).

10.1. "Взлетная" и "посадочная" площадки

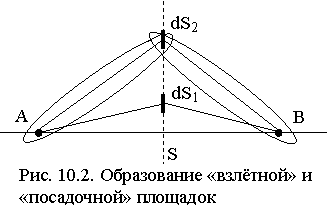Покажем, что в результате поглощения радиоволн земной толщей при прохождении трассы вдоль земной поверхности энергетический вклад первой зо­ны Френеля в принимаемый сигнал уменьшается. Существенный участок для распространения радиоволн вдоль поверхности идеально прово­дящей земли имеет форму эллипса с фокусами в точке излучения A и в точке приема B. В случае реальной земли электромагнитное поле будет убывать вследствие просачивания энергии в землю. Рассмотрим элементарные площадки dS1 и dS2 в плоскости S, перпендикулярной к поверхности (рис. 10.2). Сравним вклады в принимаемое поле вторичных источников на этих площадках. Согласно принци­пу Гюйгенса–Френеля, чем ближе площадка к прямой AB, тем больше ее вклад в поле в точке B. Но, по мере приближения к полупроводящей поверхности, возрастает поглощение ею радиоволн. Следовательно, вклад в принимаемое поле вторичных источников более высоко расположенных участков плоскости S может стать более существенным, т. е. вклад dS2 может быть больше вклада участка dS1. Это можно трактовать как отклонение траектории распространения волны от прямолинейной – её "выпячивание". При этом существенно повышается роль участков поверхности, непосредственно примыкающих к точкам приема и передачи, по сравнению со средними участками трассы. Ведь в формировании сигнала зонами Френеля высокого порядка участвуют как прямые, так и отраженные от поверхности под большим углом лучи, а последние создаются вторичными источниками, расположенными вблизи точек передачи и приема. Отсюда - обоснованность предложенных названий этих областей: "взлетная" и "посадочная" площадки.

10.2. Распространение радиоволн вдоль неоднородной трассы

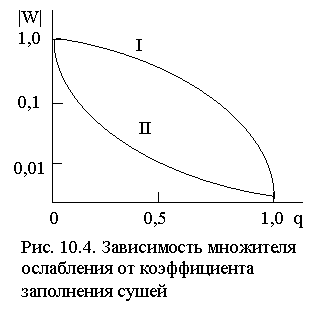
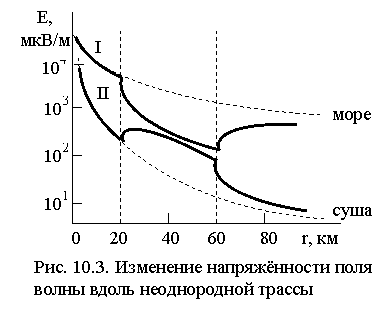Электрические параметры почвы вдоль трассы распространения радиоволн не постоянны. Учёт этого обстоятельства в общем случае весьма сложен. Наи­больший интерес представляет случай резкого изменения свойств поверхности при переходе трассы с моря на сушу, и наоборот. На рис. 10.3 приведена зависимость от расстояния функции ослабления для слу­чая последовательного распространения радиоволн над участками поверхности: "море-суша-море" (I) и "суша-море-суша" (II). В первом случае напряжённость поля в точке приёма получается близкой к случаю распространения над однородной сушей, во втором - ­к случаю однородной морской трассы. В обоих случаях основное влияние на величину поля в точке приема оказывают концевые участки трассы. Наглядно это влияние представлено приведённой на рис. 10.4 зависимостью множителя ослабления |W| от коэффициента за­полнения трассы сушей 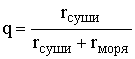. Видим, что если концевые участки трассы находятся на суше, то даже при малом q множитель поглощения почти так же мал, как и для случая полностью сухопутной трассы. Если же концевые участки трассы находятся на море, влияние суши становится существенным только при q ³ 0,9. В целом, когда приемная и передающая антенны расположены на суше, поле в точке приёма может быть почти на 2 порядка меньше по сравнению со случаем расположения антенн вблизи поверхности хорошо проводящего моря.

10.3. Береговая рефракция

Неоднородность электрических свойств почвы вдоль наземной трассы влияет не только на уровень поля, но и на направление распространения радиоволн, вызывая пово­рот фазового фронта волны. Последнее проявляется, в частности, при прохождении ради­отрассы береговой черты под углом, отличным от прямого. Явление "береговой рефракции" в виде математической ошибки пеленга при работе береговых радиопеленгаторов было обнаружено в 1918 году. Ошибка наблюдалась, лишь если пеленгатор располагался вблизи береговой черты. По мере удаления вглубь суши ошибка уменьшалась.

Теория явления следующая. Мгновенное значение напряжённости поля на расстоянии r от излучателя

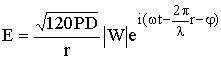,(10.4)

где j = j(r) - фазовый угол, обусловленный взаимодействием волны с земной поверхностью и являющийся функцией численного расстояния r. Изменение фазы волны с расстоянием эквивалентно изменению фазовой скорости vф. Если приравнять нулю дифференциал от фазы в (10.4):

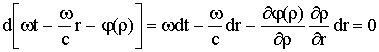
и воспользоваться представлением r (10.2), можно получить

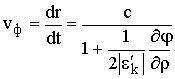. (10.5)

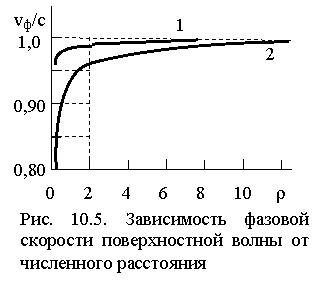
На рис. 10.5 приведена зависимость vф поверхностной волны от численного расстояния для моря (1) и для суши (2).

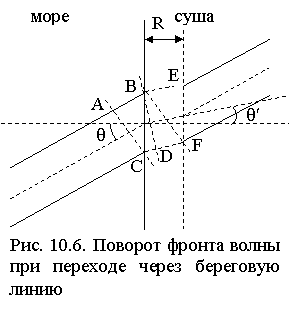Пусть фронт радиоволны с моря пересекает береговую черту под углом q (рис. 10.6). Если участок над морской поверхностью был достаточно протяженным, в точках A и C скорость волны vф » c. При переходе в точке С на сушу фазовая скорость, согласно рис. 10.5, уменьшается, в то же время на участке AB продолжается движение волны с прежней скоростью. Таким образом, фронт волны поворачивается вправо. При переходе в точке B левой части фронта волны на сушу произойдет уменьшение её фазо­вой скорости. Но к этому времени правая часть фронта уже прошла расстояние CD над сушей, и скорость ее движения возросла. Так что на участке DF должен наблюдаться поворот фронта волны до практи­ческого совпадения (когда скорость движения по всему фронту приблизит­ся к с) с первоначальным направлением.

Таким образом, в полосе суши шириной R радиовол­на, пересекающая береговую черту, меняет своё направление. Если принять для моря s = ¥ и если расстояние от точки излучения до берега ® ¥ (т. е. падающую волну можно считать плоской), то угол поворота плоскости волны /1/

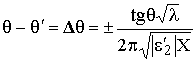, (10.6)

где |e'2| - модуль диэлектрической проницаемости сухопутного участка трассы, X - расстояние от точки приема до береговой линии, знак "-", если точка приема находится на море, и "+" для приёма ­на суше.

Из (10.6) следует, что ошибка пеленга растет с увеличением q, l и уменьшается по ме­ре удаления от береговой черты. Обычно Dq не превосходит нескольких градусов.

11. Влияние сферичности отражающей поверхности

Практически все радиотрассы, использующие земные радиоволны, можно свести к двум основным группам:

1) передающая и (или) приемная антенны расположены над поверхностью на высоте порядка нескольких l, что выполняется обычно для l < 20-30 м;

2) обе антенны расположены в непосредственной близости от поверхности, как это имеет место для ДВ, СДВ и отчасти для СВ.

Пусть приемная и передающая антенны расположены в точках A и B и подняты на высоты соответственно h1 и h2 над гладкой сферической Землёй с радиусом RЗ » 6378 км (рис. 11.1). Ес­ли соотношение между h1, h2, RЗ таково, что первая зона Френеля не дости­гает земной поверхности, то возможно прямолинейное распространение радиоволн между точками A и B. Если зона перекрывается земной поверхностью, то сферич­ность Земли является препятствием, за которое радиоволна может распространяться только путем диф­ракции. Поле в этом случае оказывается сильно ослабленным.

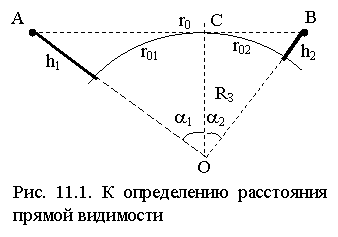Ориентировочной оценкой возможности прямолинейного распространения радиоволн является расстояние прямой видимости – расстояние между антеннами, при котором соединяющая их пря­мая линия касается земной поверхности. Найдём это расстояние. Из DACO имеем 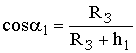, так что 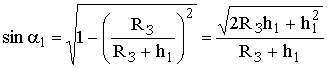. Так как h1 << RЗ, то 2RЗh1 >> h12, следовательно, 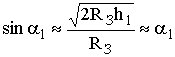, и дуга

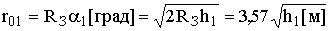, км.

Аналогичное соотношение можно получить и для дуги r02. Следовательно, расстояние прямой видимости r0 между двумя антеннами с высотами подъёма h1 и h2 над поверхностью сферической Земли

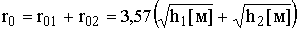, км.

В зависимости от соотношения между протяженностью радиотрассы r и расстоянием прямой видимости r0 используются следующие модели:

1) r < 0,2r0, тогда земную поверхность можно в расчетах считать плоской. Моделью плоской Земли пользуются в метровом радиодиапазоне при r < 10 ¸ 20 км, на декаметровых волнах для трасс протяженностью до нескольких десятков км, на СВ и ДВ - до нескольких сотен км.

2) 0,2r0 < r < 0,8r0, в этом случае земная поверхность еще не перекры­вает первую зону Френеля, однако её выпуклость следует учитывать. Зону r < 0,8r0 называют зоной освещенности, поле в точке приёма здесь рассчитывается с помощью интерференционных формул.

3) r > 0,8r0, тогда расчеты следует вести с помощью дифракционных формул. Об­ласть 0,8r0 < r < 1,2r0 называется зоной полутени, область r > 1,2r0 - зоной тени.

При расстояниях r < r0 для сферической поверхности по сравнению с плоскостью уменьшается разность хода Dr между прямым и отраженным лучом, определяющая по­ложение интерференционных максимумов и минимумов в точке приема. Пусть С - точка геометрического отражения (рис. 11.2). Построим в этой точке плоскость, касатель­ную к земной поверхности. Высоты точек приема и передачи над этой плоскостью h'1 и h'2 называются приведенными высотами. Если для плоской Земли разность хода лучей 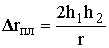(8.11), то с учётом сферичности , а поскольку h'i < hi, то и Drсф < Drпл. Уменьшает­ся и угол скольжения q (для плоскости, на сфере < qпл), соответственно должен возрасти модуль коэффициента отражения |R|. Однако этот рост ограничен уве­личением расходимости радиоволн, отраженных сферической поверхностью, что приво­дит к увеличению освещаемой площади по сравнению с отражением от плоскости (рис. 11.3). Если Sпл - плоскость сечения телесного угла пучка радиоволн, отраженных в пределах плоской существенной области отражения, а Sсф - то же для случая сферической поверхности, тогда изменение потока энергии 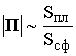, а изменение напряжённости по­ля 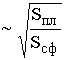. Величину 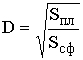называют коэффициентом расходимости, рассчитать который можно по следующей формуле:

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4