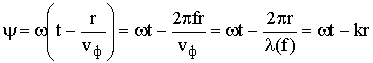,

где vф = - фазовая скорость. Таким образом, каждая монохроматическая составляющая радиосигнала распространяется со своей vф. Так как в ионосфере n(f) < 1, то vф > c.

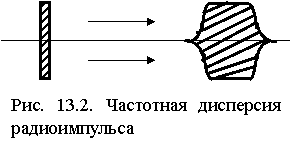
Реальный физический сигнал представляет собой совокупность бесконечного числа перемещающихся монохроматических волн, следовательно, из-за частотной дисперсии радиоимпульс по мере перемещения будет деформироваться, расплываться (рис. 13.2).

Ско­рость распространения сигнала в диспергирующей среде характеризуется групповой скоростью vгр, равной скорости распространения импульса конечной длительности, содержащего несколько различных периодов колебаний,

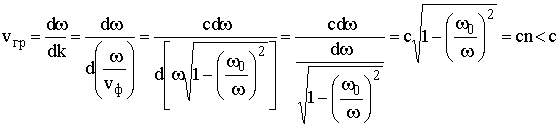.(13.12)

По сути, vгр характеризует скорость перемещения огибаю­щей ВЧ колебаний.

Так как нормаль к поверхности равных фаз совпадает с направлением распространения волны, то vф определяет траекторию движения радиоволн, а vгр - время распространения импульса по этой траектории.

13.3. Влияние магнитного поля на распространение радиоволн в ионосфере

Напряжённость магнитного поля Земли имеет в средних широтах величину H0 = 0,5 э = 40 А / м (у экватора 28 А / м, у магнитных полюсов 56 А / м), что обычно >> напряженности магнитного поля распространяющихся радиоволн. Уравнение движения электронов ионосферной плазмы с учётом магнитного поля имеет вид

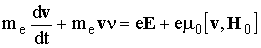, (13.13)

где последнее слагаемое определяет силу Лоренца, под действием которой электрон закручивается вокруг силовой линии магнитного поля с гиромагнитной частотой 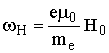. Если поле волны меняется по гармоническому закону, первые два уравнения Максвелла можно представить в виде

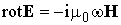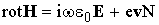, . (13.14)

Применяя к первому уравнению (13.14) операцию rot и используя второе уравнение, получаем

rot rot E = m0e0w2E - iwm0evN. (13.15)

Решая (13.15) совместно с (13.13) относительно показателя преломления n при следующих допущениях: n = 0, волна распространяется вдоль оси Ox, т. е. , , 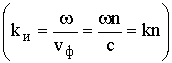можно получить

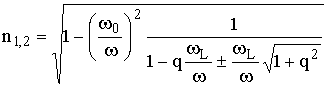, (13.16)

где

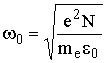- плазменная частота,

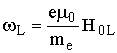- продольная гирочастота,

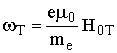- поперечная гирочастота,

(H0L, H0T - проекции H0 соответственно на направление распространения радиоволн и перпендикулярное к нему)

.

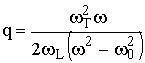Таким образом, ионосфера под влиянием магнитного поля становится двоякопреломляющей средой, и электромагнитная волна в ней расщепляется на обыкновенную (с коэффициентом преломления n1) и необыкновенную (с коэффициентом n2). Так как n1 ¹ n2, ионосфера для радиоволн является и анизотропной средой. Рассмотрим два предельных случая распространения.

1. Пусть H0 ^ v. Тогда wL = 0 и

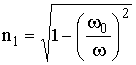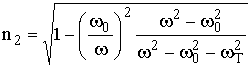, . (13.17)

Если выражение для n1 совпадает с видом n (13.11) для ионосферы без учета магнитного поля, то вид n2 существенно отличается.

2. Случай продольного распространения. В этом случае wT = 0, и из (13.16) следует, что

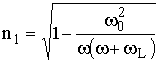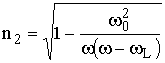, . (13.18)

Иногда и в этом приближении волну с n1 называют обыкновенной, а волну с n2 – необыкновенной волной.

В области отражения (поворота) волны выполняется условие = 1, и из выражения (13.16) в этом случае даже при малых углах a получаются формулы (13.17), т. е. в области отражения имеет место квазипоперечное распространение. На высотах ниже области отражения << 1 и, рассматривая в этом приближении выражение (13.16), приходим к формулам (13.18), справедливым даже при больших значениях угла a. Таким образом, распространение радиоволн в ионосфере носит квазипродольный характер.

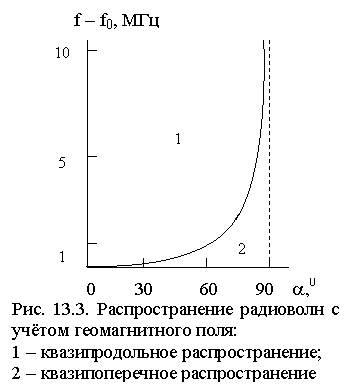Результаты расчетов, показывающие, при каких значениях угла a между направлением радиоволны и геомагнитным полем можно рассматривать это распространение или как квазипродольное, или как квазипоперечное, представлены на рис. 13.3. Из него следует, что квазипродольное распространение справедливо в весьма широком диапазоне углов a.

При отражении от ионосферы условие n = 0, согласно (13.17), выполняется: для обыкновенной волны при w = w0, для необыкновенной волны при частотах, соответствующих решению уравнения , т. е. отражение будет происходить выше и ниже обыкновеной волны. Таким образом, отражение радиоволны в ионосфере происходит на трех различных высотах. Правда, отражение необыкновенной волны наблюдается обычно только на меньшей высоте, поскольку выше уровня отражения обыкновенной волны необыкновенная составляющая сильно поглощается.

13.4. Эффект Фарадея

Воздействие ионосферы на линейно поляризованную электромагнитную волну можно представить как возбуждение двух волн с круговой поляризацией, с взаимно противоположным направлением вращения векторов E и различными коэффициентами преломления n1 и n2. Различными будут и их фазовые скорост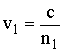и и 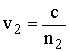. В сумме эти волны дают линейно поляризованную волну, вектор E которой по мере распространения в ионосфере поворачивается. Явление поворота плоскости поляризации в распространяющейся волне называется эффектом Фарадея. При прохождении расстояния r плоскость поляризации повернётся на угол

.

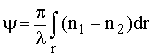На высоких частотах величину y можно рассчитать по формуле /7/

.

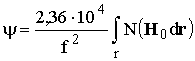Если угол между H0 и направлением распространения острый, суммарный вектор E поворачивается против часовой стрелки. При тупом угле наблюдается поворот плоскости поляризации по часовой стрелке. Вообще, плоскость поляризации поворачивается в направлении вращения вектора обыкновенной волны.

13.5. Распространение радиоволн в простом ионосферном слое

Если радиоволна излучена с земной поверхности и падает на ионосферный слой под углом j0 (рис. 13.4), дальнейшая её траектория на ионосферном участке в плоскослоистом приближении описывается уравнением

n0sinj0 = nsinj, или n0cosq0 = ncosq = Const, (13.19)

где n0 - показатель преломления нейтральной части атмосферы.

Поскольку, согласно (13.11), ниже максимума ионизации коэффициент n с ростом высоты уменьшается, из (13.19) следует, что должен расти cosq, и на некоторой высоте возможно выполнение условия cosq = 1, т. е. q = 0. Далее луч начнет распространяться обратно к Земле. Полагая n0 » 1, условие поворота луча можно записать как

n = cosq0. (13.20)

Возведём (13.20) в квадрат и используем представление (13.11):

,

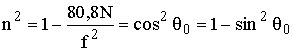откуда

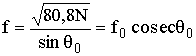. (13.21)

Здесь - плазменная частота слоя на высоте z. Поскольку q0 = p/2 - j0, из (13.21) следует известный “закон секанса”

f = f0secj0, (13.22)

связывающий значение частоты f0 вертикальной волны, отраженной от слоя на высоте z, со значением частоты луча, падающего на слой под углом j0 и отраженного на той же высоте.

С увеличением f0 высота отражения поднимается до высоты максимума ионизации слоя Nm, которой соответствует критическая частота слоя fкр = .

При наклонном распространении максимуму ионизации соответствует

fmax(j0) = fкр secj0 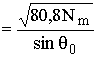(13.23)

- максимальная частота слоя для данного j0. Если f > fmax(j0), радиолуч проходит ионосферный слой насквозь.

Из (13.21) следует, что радиус кривизны траектории радиолуча в области отражения

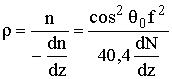. (13.24)

Пусть q0 постоянен, тогда с ростом частоты f будут расти высота отражения и радиус кривизны r. В области высоты максимума электронной концентрации Nm ® 0 и из (13.24) следует, что r ® ¥. Этим объясняется наблюдающийся иногда приём радиосигнала на расстоянии до 7 – 10 тыс. км. Такое распространение называется распространением лучом Педерсена. Выше Nm 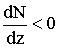, а, значит, и r < 0, что можно трактовать как искривление траектории луча вверх.

Зафиксируем теперь частоту f и будем увеличивать угол возвышения q0. Высота отражения будет расти, радиус кривизны - уменьшаться, и луч будет падать все ближе к излучателю. Однако с ростом высоты отражения мы все ближе подходим к максимуму слоя, в области которого ® 0, что начинает приводить, согласно (13.24), к увеличению r. Таким образом, начиная с некоторого q0 = qmax, дальность падения отраженного луча начнет расти. Наименьшее расстояние D до места падения луча частотой f при отражении называется радиусом зоны молчания, а соответствующая этому радиусу частота - максимально применимой частотой (МПЧ). При дальнейшем увеличении q0 используемая частота может превысить критическую для данного слоя, и радиолуч уйдёт выше.

13.6. Теоремы эквивалентности

Пусть радиолуч, будучи излученным в т. T под углом q0, претерпевает поворот в ионосфере и возвращается на землю в т. R (рис. 13.5). Участки траектории радиоволны до входа в ионосферу и после выхода из нее будем считать прямолинейными, а участок MON - искривленным. Время Dt прохождения пути MON определяется групповой скоростью

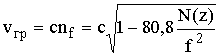(13.25)

и равно

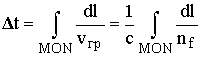. (13.26)

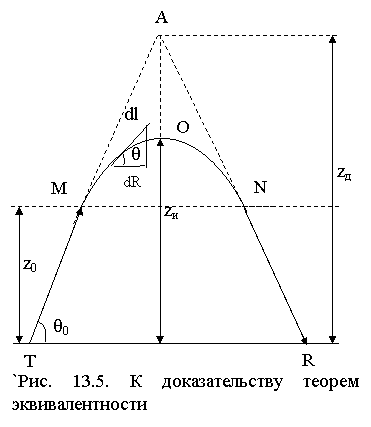Согласно рис. 13.5, 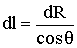. Используя это и (13.19), получаем 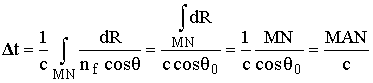. (13.27)

Выражение (13.27) представляет собой математическую трактовку первой теоремы эквивалентнос-ти (теорема Брайта-Тюва), которая гласит: время про-хождения сигналом искри-вленного участка траекто-рии в ионосфере с группо-вой скоростью vгр равно времени прохождения сиг-налом воображаемого треу-гольного пути MAN со ско-ростью света с. Путь MAN называется эквивалентным треугольным путем, а вы-сота zд - действующей вы-сотой отражения наклон-ного луча.

Вторая теорема экивалентности (теорема Мартинса): если истинные высоты отражения двух сигналов с различной частотами, распространяющихся по траекториям с различными углами наклона, равны, то равны и их действующие высоты отражения.

Докажем теорему для следующего случая. Пусть на высоте z происходит отражение как вертикального луча частотой f0, так и луча частотой f, излученного под углом места q0. Тогда частоты связаны выражением (13.21), и nf можно представить как

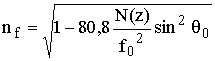. (13.28)

Из (13.19) следует, что

nf2cos2q = cos2q0 ® nf2(1 - sin2q) = cos2q0 ® nf2 = nf2sin2q + cos2q0,

откуда

. (13.29)

Подставим (13.29) в (13.28):

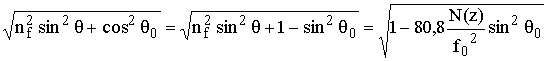.(13.30)

Возведя (13.30) в квадрат, после преобразований можно получить

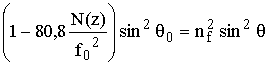, т. е.

. (13.31)

Подставим (13.31) в (13.26) и используем построение на рис. 13.5.

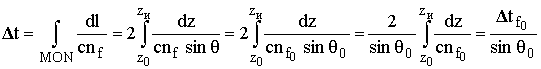, (13.32)

здесь - время распространения вертикальной волны частотой f0 до высоты zи отражения и обратно. Но, согласно (13.27), 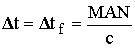, тогда из (13.32) следует, что величина

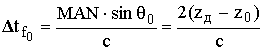(13.33)

равна времени распространения вертикального луча частотой f0 до высоты zд и обратно cо скоростью с, что и требовалось доказать. Поскольку параметры наклонного луча выбраны произвольно, теорема доказана.

13.7. Вертикальное зондирование ионосферы

Производится с целью определения высотного профиля ионизации. Выполняется с помощью ионосферной станции, в состав которой входят:

а) передатчик, генерирующий радиоимпульсы длительностьюмкс с частотой повторениякГц и пиковой мощностью до десятков кВт. Несущая частота может плавно меняться от 0,5 до 20 МГц за 1 - 2 мин – интервал, за который состояние ионосферы существенно не меняется;

б) широкодиапазонный приемник;

в) широкодиапазонная антенна с хорошей направленностью (например, вертикальная ромбическая антенна);

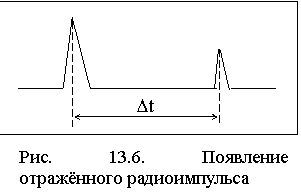
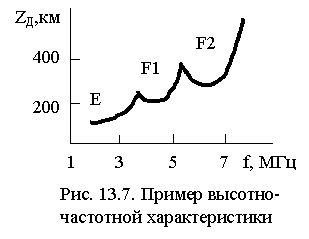
г) индикаторное устройство, типичный результат работы которого представлен на рис. 13.6. Dt - через этот промежуток времени в приемник попадает отраженный импульс, пришедший с высоты zотр, на которой 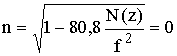. Шкала горизонтальной развертки обычно калибруется в значениях действующей высоты zд. Изменяя несущую частоту, получают зависимость zд(f), называемую ВЧХ - высотно-частотной характеристикой. Пример ВЧХ представлен на рис. 13.7.

Рассмотрим распространение импульса вертикально вверх со скоростью vгр = сn. По мере проникновения в ионосферный слой n уменьшается, и при n = 0 (т. е. при vгр = 0) происходит отражение импульса. Время запаздывания отраженного импульса относительно момента излучения

,

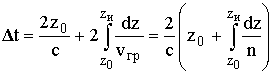где z0 - высота основания ионосферы. Действующая высота отражения

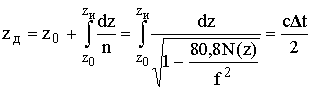(13.34)

есть воображаемая высота, до которой распространяется луч, если считать его скорость = с. Так как c > vгр, то и zд > zотр. Интеграл в (13.34), хотя и является несобственным (при z = zи подынтегральная функция ® ¥), однако сходится.

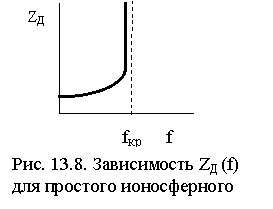
Зависимость zд от частоты f, которая должна наблюдаться при вертикальном зондировании простого ионосферного слоя, приведена на рис. 13.8.

Для пересчета zд в истинную высоту отражения применяются различные методы: задание закона изменения N с высотой, метод Эплтона и т. д.

13.8. Поглощение в ионосфере

Поскольку ионосфера является проводящей средой, амплитуда распространяющейся в ней плоской радиоволны уменьшается по закону , где - показатель затухания, в котором p определяется согласно (2.8).

В низкочастотном диапазоне 60sl >> e¢, тогда из (2.9) следует, что

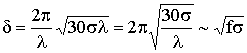. (13.35)

При w2 << n2 из (13.7) получаем 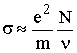, следовательно, 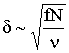, т. е. с увеличением частоты f поглощение растет.

На высоких частотах при 60sl << e¢, согласно (2.10), 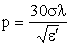. Полагая, что при w >> w0 величина 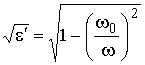» 1 , и что для w2 >> n2 из (13.8) следует 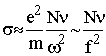, получаем 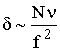, т. е. в высокочастотном диапазоне поглощение с ростом частоты падает.

Таким образом, в ионосфере зависимость поглощения от частоты имеет максимум в области w » n. Пример частотной зависимости коэффициента поглощения приведён на рис. 13.9.

В нижней части ионосферы n » 107, т. е. условие максимального поглощения выполняется для волн с l » 200 м. Таким образом, радиоволны диапазона СВ должны сильно поглощаться в нижней ионосфере, что и наблюдается на практике.

ЛИТЕРАТУРА

1.  . Распространение радиоволн. М., Сов. Радио, 1972, 464 с.

2.  . Распространение радиоволн. М., Высшая школа, 1975, 280 с.

3.  . Электродинамика и теория относительности. М., Высшая школа, 1964, 424 с.

4.  . Распространение электромагнитных волн и ионосфера. М., Наука, 1972, 564 с.

5.  , . Электродинамика и распространение радиоволн. М., Наука, 1989, 544 с.

6.  . Флуктуационные процессы при распространении радиоволн. М., Связь, 1971, 180 с.

7.  , , . Распространение радиоволн

при космической связи. М., связь, 1969, 156 с.

 [ю1]

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4