Министерство образования Российской Федерации
Уральский государственный технический университет
РАСПРОСТРАНЕНИЕ РАДИОВОЛН
В МОБИЛЬНОЙ СВЯЗИ
Методические указания по курсу
“Распространение радиоволн и антенно-фидерные устройства в системах мобильной связи”
для студентов всех форм обучения
радиотехнических специальностей
Екатеринбург 2000
УДК 621.38
Составители ,
Научный редактор доц., канд. техн. наук
РАСПРОСТРАНЕНИЕ РАДИОВОЛН В МОБИЛЬНОЙ СВЯЗИ: Методические указания по курсу “Распространение радиоволн и антенно-фидерные устройства в системах мобильной связи”/ , . Екатеринбург: УГТУ, 20с.
Методические указания содержат краткое описание расчета радиолиний связи с подвижными объектами на открытой местности и в сложных условиях городской и промышленной застройки. Приведены выражения для расчета ослабления сигнала в свободном пространстве, а также с учетом влияния земной поверхности и затеняющих препятствий. Рассмотрены эффекты отражения, дифракции и рассеяния радиоволн. В каждом разделе приведены практические упражнения.
Библиогр.: 6 назв. Рис.14. Табл.1.Прил.1.
Подготовлено кафедрой «Высокочастотные средства
радиосвязи и телевидения».
радиосвязи и телевидения”.
Ó Уральский государственный
технический университет, 2000
Целью данных методических указаний является научить студентов рассчитывать радиоканал связи между передающей и приемной антеннами в свободном пространстве и реальных условиях и связывать принятую мощность с напряжением в приемнике и амплитудой электрического поля, изучить технику анализа отражения, рассеяния и дифракции радиоволн, научиться учитывать влияние земной поверхности с помощью двухлучевой модели распространения радиоволн, уметь проводить оценку напряженности электромагнитного поля в условиях города.
ВВЕДЕНИЕ
Путь радиоволны от передатчика к приемнику в системах мобильной связи крайне разнообразен: от их прямой видимости до сильно закрытого препятствиями, домами, деревьями пути. В отличие от проводной связи, где параметры постоянны, в беспроводной связи радиоканалы имеют существенно случайные параметры, часто сложно анализируемые. Моделирование радиолинии - наиболее сложная задача проектирования радиосистем. Оно в основном выполняется статистически с использованием данных экспериментов, выполненных порой именно для такой же или аналогичной системы.
Механизм распространения радиоволн в системах связи различен, но в основном может быть представлен отражением, дифракцией и рассеянием. Большинство сотовых систем работают в городах, где нет прямой видимости антенн передатчика и приемника, а наличие высоких зданий вызывает большие дифракционные потери. Благодаря многократным переотражениям от различных объектов, радиоволны проходят различный путь. Интерференция этих волн вызывает сильное изменение уровня сигнала от положения абонента.
Моделирование распространения радиоволн основано на предсказании среднего уровня принимаемого сигнала на заданном расстоянии от излучателя, а также в определении разброса его значений в зависимости от конкретной ситуации на трассе. Расчет радиолинии позволяет определить зону обслуживания передатчика. Моделирование среднего уровня сигнала в зависимости от расстояния между передатчиком и приемником называется крупномасштабным моделированием, поскольку позволяет определить сигнал на большом удалении (несколько сотен и тысяч метров). С другой стороны, модели характеризуют быстроменяющиеся значения уровня принимаемого сигнала на малых смещениях (несколько длин волн) или за короткое время (секунды) - они называются мелкомасштабными моделями.
При перемещении мобильного приемника на малые расстояния принимаемый сигнал может меняться очень сильно. Это происходит из-за того, что принимаемый сигнал представляет собой сумму многих волн, приходящих с различных направлений, проходящих разное расстояние и имеющих различную амплитуду и фазу. Суммарный сигнал подчиняется закону Релея. В зависимости от трассы радиоканала мелкомасштабная девиация может меняться на 3-4 порядка, т. е. уровень сигнала может меняться на 30-40 дБ (рис.1). Если мобильный приемник будет достаточно далеко, средний уровень сигнала убывает. Ниже будет рассматриваться крупномасштабная зависимость сигнала на входе приемника.
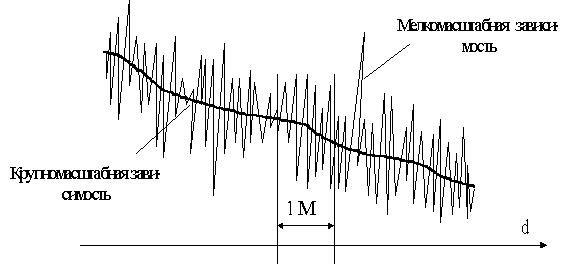
Рис.1. Изменение напряженности поля в зависимости от расстояния до передающей антенны с учетом влияния случайных факторов на частоте 1800 МГц
2. РАСПРОСТРАНЕНИЕ ВОЛН В СВОБОДНОМ ПРОСТРАНСТВЕ
Модель распространения волн в свободном пространстве используется для расчета принятого сигнала в условиях, когда передающая и приемная антенны находятся на открытой незатененной препятствиями радиолинии. Эта модель применяется для анализа радиоканалов связи через спутники и для наземных радиолиний, работающих в диапазоне сверхвысоких частот. Мощность, принятая приемной антенной с усилением Gr, которая излучается антенной передатчика мощностью Pt c коэффициентом усиления Gt на длине волны l на расстоянии d на открытом неограниченном пространстве, рассчитывается по формуле
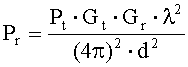 . (1)
. (1)
Коэффициент усиления антенны определяется следующим образом:
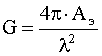 , (2)
, (2)
где Аэ - эффективная площадь поверхности антенны, м2.
Длина волны связана с несущей частотой соотношением
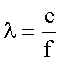 , (3)
, (3)
где с - скорость света.
Принимаемая антенной мощность в соответствии с (1) убывает с ростом расстояния d со скоростью 20 дБ на декаду, т. е. пропорционально множителю ![]()
![]() .
.
Потери передачи в радиоканале (отношение принятой и излученной мощностей)
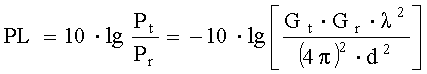 , дБ. (4)
, дБ. (4)
Для изотропных антенн (коэффициент усиления каждой из них G=1)
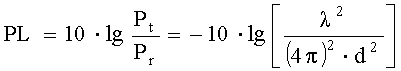 , дБ. (5)
, дБ. (5)
Предыдущие выражения верны только для дальней зоны (или зоны Фраунгофера). Граница дальней зоны определяется условием:
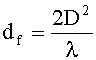 , (6а)
, (6а)
где D - наибольший размер антенны.
Дополнительным условием дальней зоны должно быть выполнение соотношений:
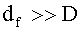 , (6б)
, (6б)
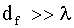 . (6в)
. (6в)
На больших расстояниях при расчете напряженности поля в точке приема иногда используют значение принимаемой мощности на некотором фиксированном расстоянии d0 - Pr (d0 ). Тогда на ином расстоянии d:
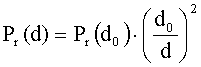 ,
, 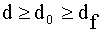 . (7)
. (7)
Т. к. изменение уровня принимаемой мощности от расстояния очень велико, используют отсчет мощности в дБмВт (дБ по отношению к 1 милливатту) и дБВт (дБ по отношению к 1 ватту):
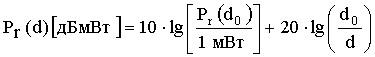 ,
, 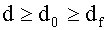 , (8)
, (8)
где Pr (d 0 ) подставляется в Вт.
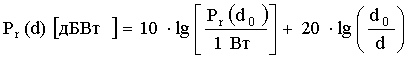 .
.

Опорное расстояние d0 обычно выбирается равным 100 м или 1 км для связи вне зданий. Для радиоканалов внутри зданий типичное значение опорного расстояния d 0 = 1 м.
Иногда в расчетах используется параметр - эффективная излучаемая мощность (![]() ), который показывает, во сколько раз плотность потока мощности в точке расположения приемной антенны при излучении мощности Pt будет больше при использовании антенны с коэффициентом усиления Gt по сравнению с изотропной антенной. Выражение
), который показывает, во сколько раз плотность потока мощности в точке расположения приемной антенны при излучении мощности Pt будет больше при использовании антенны с коэффициентом усиления Gt по сравнению с изотропной антенной. Выражение
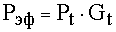 (9)
(9)
показывает максимальную излучаемую мощность в направлении максимального излучения.
Плотность потока мощности на расстоянии d от передающей антенны:
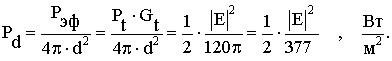
(10)
где 377 Ом - характеристическое сопротивление свободного пространства,
Е - амплитуда электрического поля на расстоянии d, В/м.
Принимаемая мощность (мощность, перехватываемая приемной антенной из падающей плоской волны)
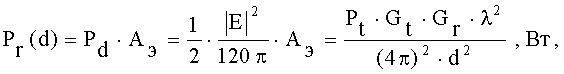 (11)
(11)
где AЭ - эффективная площадь поверхности приемной антенны, м2.
Эквивалентная схема приемной антенны, включенной на вход приемника, показана на рис.2. При условии согласования входного сопротивления антенны и приемника (![]() ) напряжение на входе последнего будет равно половине ЭДС антенны. Действующее напряжение U связано с принятой мощностью выражением
) напряжение на входе последнего будет равно половине ЭДС антенны. Действующее напряжение U связано с принятой мощностью выражением
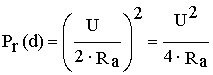 . (12)
. (12)
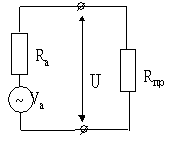
Рис.2. Эквивалентная схема приемной антенны, включенной на вход приемника
Напряжение на входе приемника определяется по формуле
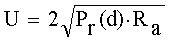 , В. (13)
, В. (13)

3. ТРИ ОСНОВНЫХ СПОСОБА РАСПРОСТРАНЕНИЯ РАДИОВОЛН
1. Отражение - имеет место при падении волны на объекты с размерами много больше длины волны. Наблюдаются, например, отражения от земли, стен зданий и т. п.
2. Дифракция - явление возникновения вторичных волн при падении радиоволны на препятствие с острыми кромками. Дифракцией обусловлено наличие поля за препятствиями в зоне геометрической тени. На высоких частотах дифракция, как и отражение, существенно зависит от геометрии объекта, а также амплитуды, фазы и поляризации поля.
3. Рассеяние - имеет место при распространении волны в среде с мелкими объектами (меньше длины волны).
3.1. Отражение радиоволн
3.1.1. Отражение радиоволн от плоской границы раздела двух сред
Если волна падает на границу раздела сред с разными параметрами, наблюдается частичное прохождение волны во вторую среду.
Амплитуды поля падающей Ei и отраженной Er волн связаны через коэффициенты отражения Френеля Г, а прошедшая Et волна - через коэффициент прохождения Т:
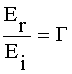 ,
, 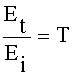 .
.
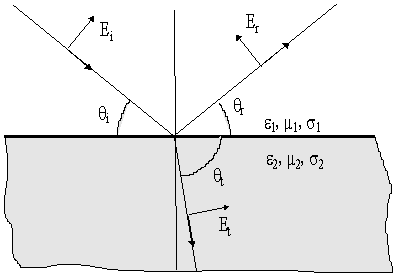
Рис.3. Отражение и преломление волн на границе раздела сред
Падающая волна произвольной поляризации раскладывается на две: с вертикальной и горизонтальной поляризацией.
В диэлектрике с потерями диэлектрическая проницаемость имеет комплексный характер:
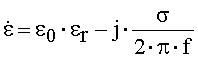
![]() , (14)
, (14)
где er - относительная диэлектрическая проницаемость cреды, s - проводимость среды, Cм/м. В хороших проводниках, когда выполняется условие f < s/e0er, вещественной частью в (14) можно пренебречь.
Коэффициент отражения для поля вертикальной поляризации
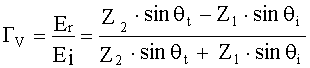 . (15)
. (15)
Коэффициент отражения для поля горизонтальной поляризации
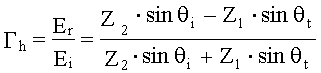
![]() , (16)
, (16)
где Zi - характеристическое сопротивление 1-й или 2-й среды.
![]() .
.
Граничные условия требуют выполнения соотношений:
q i = q r, (17)
E r = Г. E i, (18а)
E t = (1 + Г) . E i. (18б)
Если первая среда - свободное пространство (e1=1), а вторая среда не обладает магнитными свойствами (m1 = m0 ), то выражения (15), (16) упрощаются:
![]()
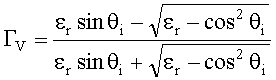 , (19)
, (19)
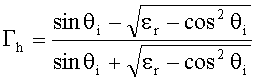 . (20)
. (20)
Для углов падения, близких к скользящим ![]() , коэффициенты отражения
, коэффициенты отражения 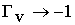
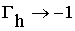 .
.
 |
Для некоторого угла
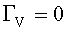 . Этот угол называется углом Брюстера qБР (угол, для которого нет отраженной волны вертикальной поляризации):
. Этот угол называется углом Брюстера qБР (угол, для которого нет отраженной волны вертикальной поляризации):
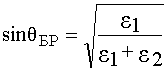 . (21)
. (21)
Если первая среда - воздух, а диэлектрическая проницаемость второй среды er, то
|
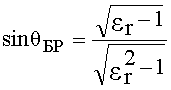 . (22)
. (22)
|
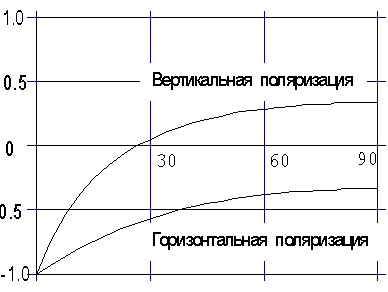
Рис.4. Зависимость коэффициента отражения волны вертикальной
и горизонтальной поляризации от угла падения ![]() ,
,
падающей на поверхность сухой земли (er = 4)

Угол Брюстера имеет место только для вертикальной поляризации поля.
3.1.2. Отражение от поверхности идеального проводника
В случае падения плоской волны на поверхность идеального проводника происходит полное отражение.
Если вектор ![]() лежит в плоскости падения (вертикальная поляризация), то
лежит в плоскости падения (вертикальная поляризация), то
![]() , (23)
, (23)
![]() . (24)
. (24)
Для случая, когда вектор ![]() перпендикулярен плоскости падения (горизонтальная поляризация),
перпендикулярен плоскости падения (горизонтальная поляризация),
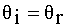 , (25)
, (25)
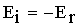 . (26)
. (26)
Из (следует, что для углов падения, близких к скользящим, коэффициенты отражения ![]() и
и ![]() .
.
3.1.3. Отражение от поверхности земли (2- лучевая модель)
В задачах мобильной связи прямое распространение радиоволн между передающей и приемной антеннами встречается достаточно редко, поэтому модель распространения волн в свободном пространстве имеет ограниченное применение. Полезная для практики двухлучевая модель распространения волн (рис.5) основана на законах геометрической оптики.
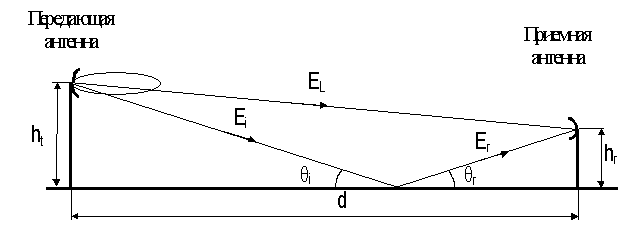
Рис.5. Прямой и отраженный лучи в точке приема радиоволн
Суммарное поле в точке приема обусловлено влиянием прямого и отраженного от земной поверхности лучей:
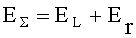 .
.
Из рис.6 видно, что разность хода прямого луча и луча с отражением от земли
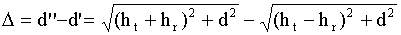 . (27)
. (27)
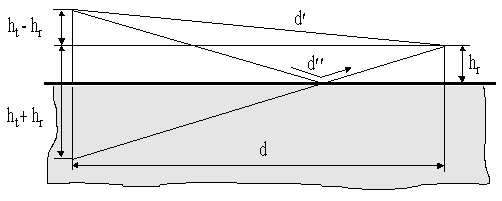
Рис.6. Мнимый излучатель поля
Если расстояние ![]() , то (27) может быть упрощено с помощью разложения Тейлора:
, то (27) может быть упрощено с помощью разложения Тейлора:
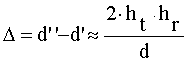 , м. (28)
, м. (28)
Тогда разность фаз прямого и отраженного лучей
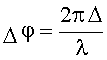 . (29)
. (29)
Суммарное электрическое поле в точке приема прямого и отраженного лучей при сделанных допущениях вычисляется по формуле
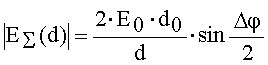 ,
, ![]() , (30)
, (30)
где Е0 - напряженность поля, создаваемая излучающей антенной на некотором опорном расстоянии d0 в свободном пространстве (без учета отражения), ![]() .
.
На больших удалениях, когда выполняется соотношение 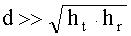 ,
,
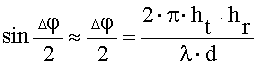 . (31)
. (31)
Суммарное поле в этом случае может быть аппроксимировано выражением
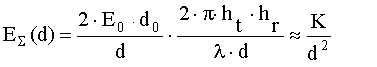 ,
,![]() , (32)
, (32)
где К - константа, связанная с амплитудой поля Е0 , высотами подвеса антенн и длиной волны. Мощность, принятая приемной антенной, пропорциональна квадрату напряженность поля:
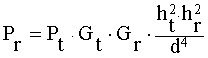 . (33)
. (33)
Из формулы (33) видно, что на больших расстояниях принятая мощность убывает обратно пропорционально d4 или 40 дБ на декаду. Это существенно быстрее, чем в свободном пространстве.
Для двухлучевой модели в соответствии с (33) потери мощности в радиоканале определяются выражением
![]() , дБ. (34)
, дБ. (34)

3.2. Дифракция радиоволн
Явление дифракции позволяет радиоволнам распространяться вокруг сферической земной поверхности за горизонт и за различные препятствия. Несмотря на перекрытие прямой видимости и существенное уменьшение уровня сигнала, он все таки остается достаточным для приема.
Феномен дифракции объясняется принципом Гюйгенса - вторичного переизлучения точек фронта волны с различной фазой (зон Френеля). Напряженность поля определяется векторной суммой вклада вторичных излучателей.
3.2.1. Геометрия зон Френеля
Пусть между излучателем и приемником расположено препятствие - экран высотой h бесконечных размеров в поперечном сечении. Расстояние от экрана до излучателя - d1 , до приемника - d2 .

Рис.7. Дифракция радиоволн на клиновидном препятствии
Ясно, что путь через кромку препятствия больше прямого. Полагая, что h<<d1,d2 и h>>l, разность хода прямого и через кромку лучей будет:
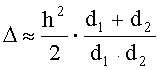 . (35)
. (35)
Соответствующая ему разность фаз
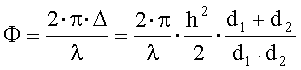 , (36)
, (36)
где используется приближение для малого аргумента tg x » x, а угол a аппроксимирован выражением
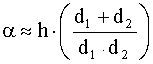 .
.
Выражение (36) может быть аппроксимировано с использованием безразмерного дифракционного параметра Френеля - Кирхгофа:
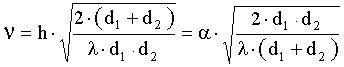 , (37)
, (37)
где a подставляется в радианах, все остальные параметры в метрах. Таким образом, разность фаз Ф может быть вычислена из выражения
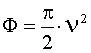 . (38)
. (38)
Из выражения (38) следует, что сдвиг фазы между прямым и дифракционным лучами является функцией высоты h и взаимного расположения препятствия, излучателя и приемника.
Дифракционные потери мощности в радиоканале могут быть объяснены с помощью зон Френеля. Зоны Френеля представляют собой области, разность хода через которые от излучателя до приемника составляет nl/2 по сравнению с прямым лучом ( l - длина волны, n - целое число).
В мобильной связи обычно наблюдается затенение части зон (источников вторичных волн) и, следовательно, уменьшение доли принятой мощности. В зависимости от геометрии препятствия принятая энергия определяется через векторное суммирование вторичных волн.
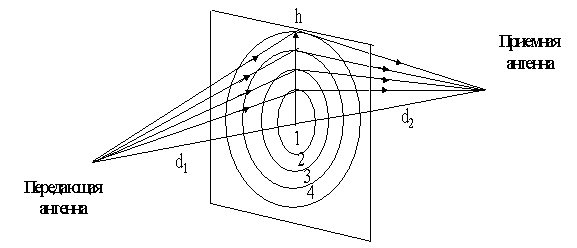
Рис.8. Формирование зон Френеля
Если препятствие не затеняет первую зону Френеля, то дифракционные потери минимальны и ими пренебрегают. Используют следующее свойство: если открыто не менее 55% первой зоны Френеля, то дальнейшее открытие первой зоны Френеля не уменьшает дифракционные потери.
3.2.2. Модель дифракции радиоволн на одиночном клине
Определение степени ослабления поля холмами и зданиями является достаточно сложной задачей при расчете зон обслуживания. Обычно точный расчет ослабления невозможен, поэтому используют методы расчета поля с необходимыми экспериментальными поправками.
Препятствие в виде одиночного холма или горы может быть обсчитано с использованием модели клина. Это простейшая модель препятствия, и быстрый расчет ослабления возможен с использованием классического решения Френеля для дифракции поля на полуплоскости.
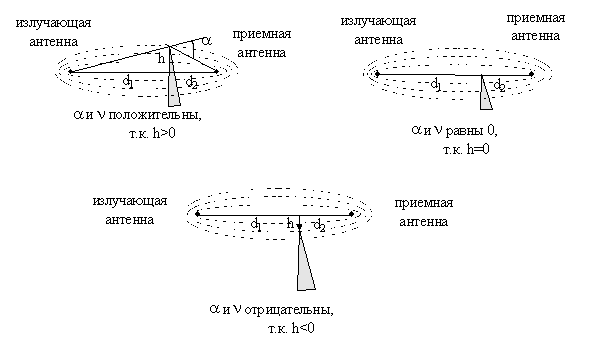
Рис.9. Варианты перекрытия видимости антенн препятствием
Напряженность поля в точке расположения приемной антенны определяется векторной суммой вторичных источников, лежащих в плоскости, расположенной над препятствием. Напряженность поля при дифракции на клине определяется выражением
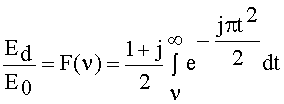 , (39)
, (39)
где Е0 - напряженность поля в точке расположения приемной антенны при отсутствии препятствия и земли, а F(n) - комплексный интеграл Френеля. Значение интеграла F(n) определяется из графиков и таблиц.
Коэффициент дифракционного усиления с препятствием (обычно он меньше 1) по сравнению со свободным пространством
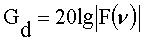 , дБ. (40)
, дБ. (40)
График этой функции показан на рис.10.
Gd, дБ n
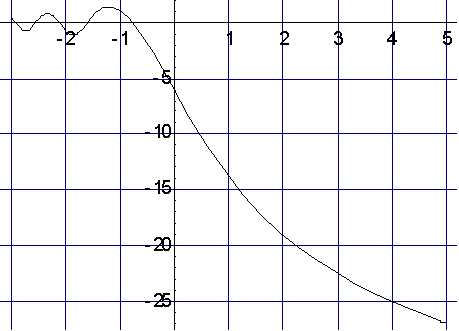
Рис.10. Зависимость коэффициента дифракционного усиления
от значения параметра дифракции n
Приближенно можно считать:
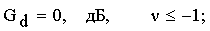 (41a)
(41a)
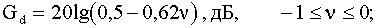 (41б)
(41б)
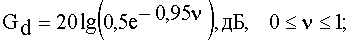 (41в)
(41в)
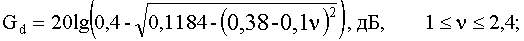 (41г)
(41г)
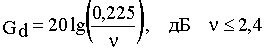 (41д)
(41д)
 |
2.2.3. Дифракция на нескольких клиньях
Если на пути между излучателем и приемником имеется несколько препятствий, то все они аппроксимируются одним эквивалентным препятствием (рис.11).
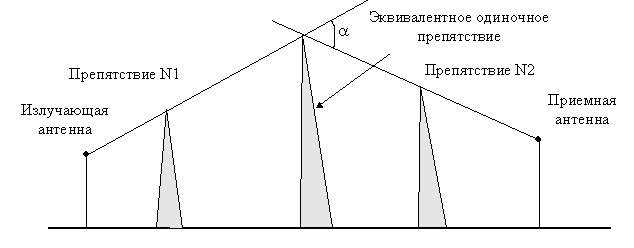
Рис.11. Эквивалентное клиновидное препятствие в задаче связи
с двумя препятствиями
Эта модель хорошо работает для двух препятствий, для нескольких - возникают определенные математические трудности.
2.3. РАССЕЯНИЕ РАДИОВОЛН
Потери от рассеяния радиоволн на препятствиях обычно много меньше потерь отражения и дифракции. Это объясняется тем, что рассеяние волн происходит во всех направлениях (на таких объектах, как мачты, лампы, деревья и т. д.).
Плоские поверхности с размерами много больше длины волны могут моделироваться как отражающие поверхности. Однако наличие неровностей изменяет отражение. Неровность поверхности определяется критерием Релея, который определяет критическую высоту hc неровностей при падении волны под углом qi:
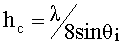 . (42)
. (42)
Поверхность считается гладкой, если разброс минимальных и максимальных высот меньше hc. Для неровных поверхностей коэффициент отражения Г умножается на коэффициент потерь рассеяния ps.
Полагая, что высота неровностей h распределена случайным образом с гауссовым законом распределения, коэффициент потерь рассеяния
 , (43)
, (43)
где sh - стандартная девиация высоты поверхности вокруг среднего значения высоты. После некоторых уточнений коэффициент потерь рассеяния с хорошим совпадением с практикой определяется выражением
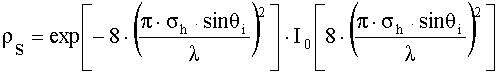 , (44)
, (44)
где I0 - функция Бесселя первого рода нулевого порядка. Коэффициент отражения электромагнитного поля для неровностей h>hc определяется выражением
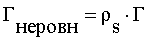 . (45)
. (45)
Степень рассеяния радиоволн от препятствий больших размеров, например, крупных домов, может характеризоваться поперечником рассеяния. Поперечник рассеяния объекта (RCS) определяется как отношение плотности потока мощности рассеянного поля в направлении приемника к плотности потока мощности, падающей на рассеивающий объект, и имеет размерность м2. Анализ основан на геометрической теории дифракции и физической оптике и может быть использован для задач расчета поля, рассеянного большими зданиями. Для городских условий используется бистатическое уравнение излучения, описывающее распространение волны в свободном пространстве и поле, рассеянное между объектами и затем переизлученное в направлении приемника.
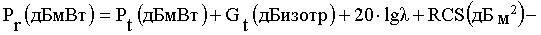
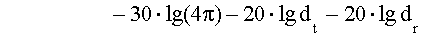 , (46)
, (46)
где dt и dr - расстояние от рассеивающего объекта до излучателя и приемника. Это уравнение корректно для дальней зоны излучателя и приемника.
3. ПРАКТИЧЕСКИЕ МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ ДЛЯ РАСЧЕТА ОСЛАБЛЕНИЯ СИГНАЛА В РАДИОКАНАЛАХ
Большинство моделей, используемых при решении задач распространения радиоволн, учитывают одновременно аналитические и экспериментальные данные. Экспериментальный подход основан на использовании графиков и аналитических выражений, описывающих данные предварительных измерений. Преимущество этого подхода состоит в учете большинства факторов, влияющих на распространение радиоволн. Иногда в задачах мобильной связи используются классические модели радиолиний, которые позволяют моделировать в крупном масштабе линии связи. Например, двухлучевая модель позволила предсказать работоспособность сотовых систем до их появления. Ниже представлены некоторые модели радиолиний.
3.1. Потери передачи в удаленных линиях
Как теоретические, так и экспериментальные исследования подтвердили, что принимаемая мощность изменяется по логарифмическому закону. Этот закон выполняется как для радиолиний вне зданий, так и внутри их. Средние крупномасштабные потери при произвольном расстоянии излучатель - приемник описываются выражением
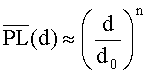 (47)
(47)
или в логарифмическом масштабе
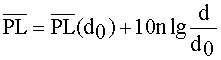 , дБ, (48)
, дБ, (48)
где n - показатель степени, который показывает, с какой скоростью возрастают потери передачи от расстояния; d0 - расстояние от излучателя до границы отсчета, d - расстояние между излучателем и приемником. Черта в (47), (48) означает среднее из возможных значений потерь для данного расстояния d. На диаграмме в логарифмическом масштабе график ослабления описывается наклонной прямой с коэффициентом наклона 10.n дБ на декаду. Показатель n зависит от конкретных параметров среды распространения.
Показатель n ослабления поля для различных условий распространения радиоволн
|
Среда |
Показатель n |
|
Свободное пространство |
2 |
|
Сотовая связь в городе | |
|
Сотовая связь в городе в тени |
3 - 5 |
|
В зданиях при прямой видимости | |
|
Препятствия, загромождения в зданиях |
4 - 6 |
Важно правильно выбрать подходящее расстояние d0 для исследования условий распространения. В сотовой связи с большими зонами действия обычно используется расстояние 1 км, в микросотовых системах много меньше - 100 м. Это расстояние должно соответствовать дальней зоне антенны для исключения эффектов ближнего поля. Эталонное значение ослабления рассчитывается с помощью формулы распространения в свободном пространстве (4) или через поля, измеренные на расстоянии d0 .
Уравнение (48) не учитывает того, что параметры среды могут быстро изменяться между измерениями. Измерения показали, что величина ослабления мощности в радиоканале описывается нормально-логарифмическим (равномерным в дБ) законом:
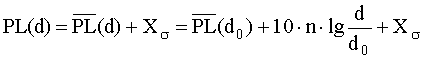 , дБ, (49a)
, дБ, (49a)
и
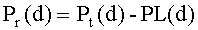 , дБ, (49б)
, дБ, (49б)
где xs - случайная величина c нормально-логарифмическим законом распределения со стандартной девиацией s, дБ.
Данные формулы могут быть использованы для расчета поля в реальных системах связи при наличии случайных ослабляющих сигнал факторов. На практике величины n и s обычно определяются из экспериментальных исследований (рис. 12).
Поскольку значение PL(d) - случайная величина с нормальным распределением по шкале дБ от расстояния d, также случайно распределена и функция Pr(d). Для определения вероятности того, что принятый сигнал будет выше (или ниже) особого уровня, может быть использована функция Q:
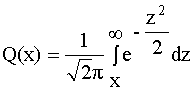 , (50а)
, (50а)
где выполняется условие ![]() . (50б)
. (50б)
Вероятность того, что принятый сигнал будет выше некоторой заданной величины g, может быть вычислена из накопительной функции плотности как
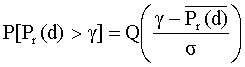 . (51)
. (51)
Аналогично вероятность того, что принятая мощность будет меньше g:
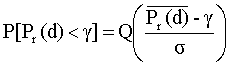 (52)
(52)
|
|
|
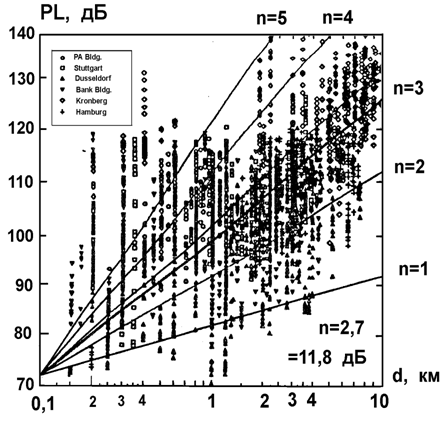
Рис.12. Экспериментальные данные, иллюстрирующие ослабление радиоволн в условиях города (приведены данные измерений ослабления мощности радиоканалов для 6 городов Германии, из этих экспериментальных данных определены параметры n=2.7, s=11.8 дБ)
|
3.2. Модели радиолиний вне зданий
Радиолинии в мобильной связи часто проходят по неровным местностям. В этом случае следует учитывать реальный профиль трассы. Трасса может изменяться от гладкой до сильно пересеченной местности. Также следует учесть наличие зданий, деревьев и других препятствий при связи в условиях города. Негладкие трассы рассчитываются разными методами. Существующие методы расчета поля в реальных условиях связи сильно отличаются по подходу, сложности и точности. Большинство основано на использовании экспериментальных данных для обслуживаемого района. Ниже описаны некоторые методы.
3.2.1. Метод Okumura
Этот метод является одним из широко используемых методов для расчета радиолиний в условиях города. Он пригоден для частот МГц (хотя может быть экстраполирован до 3000 МГц) и расстояний от 1 до 100 км. Данный метод может быть использован, если эффективная высота подвеса базовой антенны составляет от 01.01.01 м.
Okumura предложил сетку кривых для расчета среднего ослабления относительно ослабления в свободном пространстве Amu в условиях города с квазигладким профилем с изотропной передающей антенной, поднятой на эффективную высоту hte = 200 м и мобильной антенной высотой hre = 3 м. Графики получены в результате многих измерений с ненаправленными антеннами базовой станции и мобильного приемника и представлены в виде графика для диапазона частот МГц как функция дальности от 1 до 100 км.
Для определения потерь на радиолинии рассчитывается ослабление поля в свободном пространстве, затем по кривым графика (рис.13) определяется величина Ama(f, d) и добавляются к ослаблению в свободном пространстве с корректирующей поправкой, зависящей от степени неровности профиля трассы:
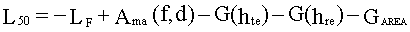 , дБ, (53)
, дБ, (53)
где L50 - средняя величина потерь,
LF - потери в свободном пространстве,
Ama - усредненное дополнительное ослабление, обусловленное влиянием земной поверхности,
G(hte) - эффективное усиление передающей антенны,
G(hre) - эффективное усиление приемной антенны,
GAREA - поправочный коэффициент из графика на рис.14.
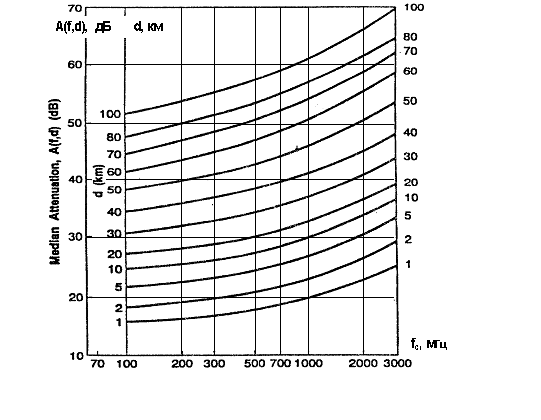
Рис.13. Частотная зависимость усредненного ослабления
сигнала по отношению к свободному пространству
для квазигладкого профиля трассы
|
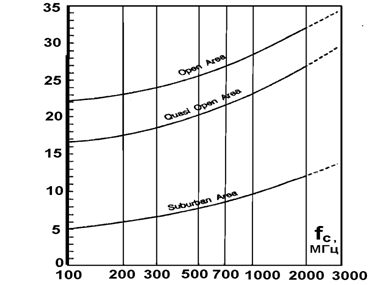
Рис.14. Поправочный коэффициент, обусловленный профилем радиотрассы
Кроме того, Okumura нашел, что величина G(hte) изменяется по закону 20 дБ/декада, а G(hre) для высот менее 3 м - 10 дБ/декада:
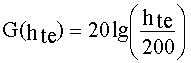 , 1000 м > h te> 10 м; (54а)
, 1000 м > h te> 10 м; (54а)
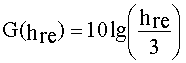 , hre < 3 м; (54б)
, hre < 3 м; (54б)
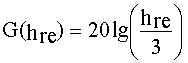 , 10 м > hre >3 м. (54в)
, 10 м > hre >3 м. (54в)
Модель Okumura полностью построена на экспериментальных данных. Графики, полученные Okumura, можно экстраполировать. Модель Okumura наиболее простая и достаточно точная для расчета потерь в сотовых системах связи и мобильной связи. Она является стандартом при расчете сот для мобильной связи в Японии.
Главный недостаток модели - работа с графиками и невозможность полноценно учесть быстроизменяющиеся условия в профиле трассы.
В основном рассмотренный метод используется для расчета радиолиний в урбанизированных и сверхурбанизированных районах. Разница расчетных и экспериментально измеренных напряженностей поля обычно не превышает 10-13 дБ.

3.2.2. Модель Hata
Hata обработал экспериментальные данные Okumura для частот МГц и предложил рассчитывать потери распространения в условиях города по стандартной формуле с учетом корректирующих уравнений для иных условий. Стандартная формула для расчета средних потерь мощности в условиях города:
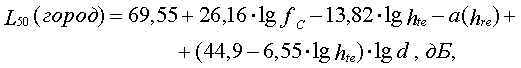 (55)
(55)
где fc - частота от 150 до 1500 МГц,
hte - эффективная высота базовой антенны (от 30 до 200 м),
hre - эффективная высота мобильной антенны (от 1 до 10 м),
d - расстояние от передатчика до приемника, км,
a(hre) - корректирующий фактор для эффективной высоты мобильной антенны, который является функцией величины зоны обслуживания.
Для небольших и среднего размера населенных пунктов:
![]() . (56)
. (56)
Для крупных городов:
![]() для fc<300 МГц; (57a)
для fc<300 МГц; (57a)
![]() для fc>300 МГц. (57б)
для fc>300 МГц. (57б)
В сверхурбанизированных районах стандартная (основная) формула Hata (55) модифицируется следующим образом:
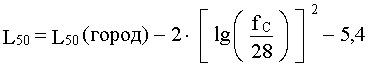 , дБ, (58)
, дБ, (58)
а для открытых районов:
![]() ,дБ. (59)
,дБ. (59)
Хотя формулы Hata не позволяют учесть все специфические поправки, которые доступны в методе Okumura, они имеют существенное практическое значение. Расчеты по формулам Hata хорошо совпадают с данными модели Okumura для дальностей, больших 1 км.
3.2.3. Уточнение метода Hata
Европейская ассоциация EVRO-COST предложила новую версию метода Hata, верную для частот до 2 ГГц. Стандартная формула для расчета средних потерь мощности в условиях города записывается следующим образом:
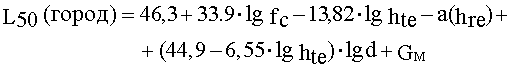 , (60)
, (60)
где a(hre) определяется формулами (56) и (57),
Gm = 0 дБ для городов средних и крупных размеров,
Gm = 3 дБ для столиц.
Допустимые границы параметров в (60): fc 1500...2000 МГц,
hte 30...200 м,
hre 1...10 м,
d 1..20 км.
Использование вышезаписанных выражений позволяет рассчитывать широкий класс радиоканалов связи с учетом конкретных условий распространения волн. Выбор конкретной модели, описывающей распространение радиоволн, существенно зависит от частоты несущей, высоты подвеса передающей и приемной антенн, окружающего пространства. Адекватность расчетов и экспериментальных данных определяется корректностью используемых методов, а также сильно зависит от практического опыта специалиста.
Настоящая работа подготовлена на основе книги "Cellular radio and personal communications" под редакцией T. S.Rappaport.
4. Решение упражнений
1. Дано: Наибольший размер антенны D=1 м
Рабочая частота fc=900 МГц
Решение:
Длина волны 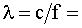 0,33 м.
0,33 м.
Используя (6а): граница дальней зоны 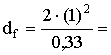 6 м.
6 м.
Проверяем: ![]() и
и ![]() .
.
Таким образом, опорное расстояние может быть ![]() =100 м или, например, 10 м.
=100 м или, например, 10 м.
Напомним, что ![]() должно быть меньше расстояния d между передатчиком и приемником.
должно быть меньше расстояния d между передатчиком и приемником.
2. Дано: Излученная мощность Pt=50 Вт
Несущая частота fc=900 МГц
Решение:
a) с использованием формулы (8) излученная мощность
![]() ;
;
б) ![]() ;
;
в) принятая мощность по формуле (1):
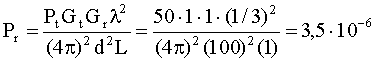 Вт.
Вт.
По формуле (8) принятая мощность:
![]() =-24,5 дБмВт;
=-24,5 дБмВт;
г) 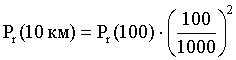 =24,5 – 40 = -64,5 дБмВт.
=24,5 – 40 = -64,5 дБмВт.
3. Дано: Излученная мощность Pt=50 Вт
Несущая частота fc=900 МГц
Коэффициент усиления передающей антенны Gt=1
Коэффициент усиления приемной антенны Gr=2
Входное сопротивление приемной антенны 50 Ом
Решение:
a) из формулы (4) принятая на расстоянии 10 км мощность:
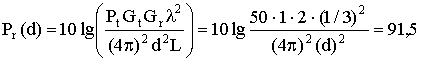 дБВт = -61,5 дБмВт;
дБВт = -61,5 дБмВт;
б) из формулы(11) амплитуда электрического поля:
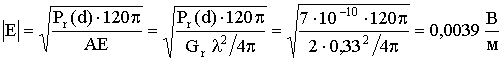 ;
;
в) из формулы(15) напряжение на входе приемника:
![]() мВ.
мВ.
4. Решение:
Подставляя qi=00 в формулу (20):
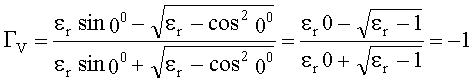 .
.
Подставляя qi=00 в формулу (21):
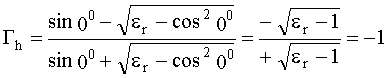 .
.
Это упражнение показывает, что при углах падения, близких к скользящим, поверхность земли может моделироваться идеальным проводником, который обеспечивает модуль коэффициента отражения, равный 1, независимо от поляризации поля и свойств подстилающей поверхности.
5. Решение:
Угол Брюстера может быть найден после подстановки значения диэлектрической проницаемости er в формулу (22):
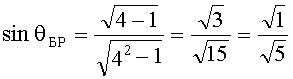 ,
,
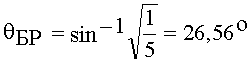 .
.
Таким образом, для er=4 угол Брюстера равен 26,560.
6. Дано: Расстояние между передатчиком и приемником d=5 км
Напряженность поля на расстоянии 1 км 10-3 В/м
Рабочая частота fc=900 МГц
Решение:
a) длина волны l=0,33 м
Длина четвертьволновой антенны ![]() см.
см.
Усиление ![]() диполя может быть определено из формулы (2) и равно 1,8 или 2,55 дБ;
диполя может быть определено из формулы (2) и равно 1,8 или 2,55 дБ;
б) так как расстояние ![]() , напряженность электрического поля вычисляется по формуле
, напряженность электрического поля вычисляется по формуле 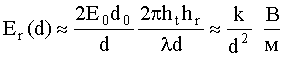 ;
;
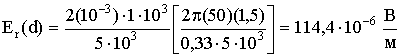 .
.
Принятая на расстоянии d мощность рассчитывается из (14):
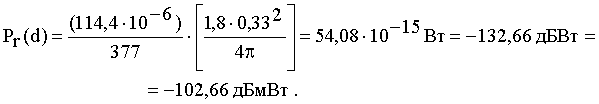
7. Дано: Длина волны 1/3 м
Расстояние d1=1 км, d2=1 км
Решение:
a) h=25 м. Из формулы (37) дифракционный параметр
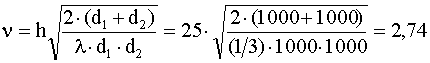 .
.
Из рис.10 дифракционные потери равны 22 дБ.
Из формулы аппроксимации (41г): дифракционные потери 21,7 дБ.
Разность хода прямого и отраженного луча из (35):
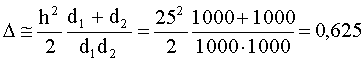 м.
м.
Для определения, в какой зоне Френеля будет верх препятствия, вычислим параметр n, который удовлетворяет формуле 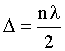 .
.
Для 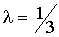 м и D = 0,625 м получим
м и D = 0,625 м получим 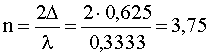 .
.
Таким образом, верх препятствия перекрывает первые три зоны Френеля;
б) при h = 0 параметр n = 0. Из рис.10 дифракционные потери равны 6 дБ. С использованием аппроксимационной формулы (41в) дифракционные потери равны 6 дБ. Для h=0 разность хода D=0. Перекрывается середина 1-й зоны Френеля;
в) h = -25 м. Из (37) n = -2,74. Из рис.10 дифракционные потери равны 1 дБ. Из формулы аппроксимации (41а) дифракционные потери равны 0 дБ. Препятствие лежит ниже трех зон Френеля, следовательно, потери незначительны и ими можно пренебречь.
8. Решение:
Минимальная квадратичная ошибка может быть найдена следующим образом. Пусть Pi - принятая мощность на расстоянии di. Пусть ![]() будет оценка мощности при использовании закона
будет оценка мощности при использовании закона 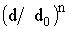 ослабления радиолинии по (49а). Сумма квадратичных ошибок между измерением и расчетом:
ослабления радиолинии по (49а). Сумма квадратичных ошибок между измерением и расчетом:
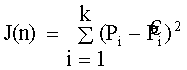 .
.
Величина n может быть получена при решении уравнения для производной функции ![]() :
:
а) используя формулу (49а), мы находим
![]()
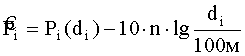 .
.![]()
Помня, что 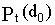 = 0 дБмВт, мы находим следующие результаты для
= 0 дБмВт, мы находим следующие результаты для ![]() (дБмВт):
(дБмВт): ![]() =0;
=0; ![]() =-3n;
=-3n; ![]() =-10n;
=-10n; ![]() =-14,77n.
=-14,77n.
Сумма квадратичных ошибок:
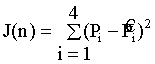 =
=
=(+ (n))2 + (n))2 + (,77n))2=
=6,8n + 327,153n2.
Взяв производную по n из предыдущего выражения, получим
![]() =654,306n - 2887,8.
=654,306n - 2887,8.
Приравнивая это уравнение нулю, получим n=4,4;
б) дисперсия 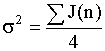 при n=4,4 может быть получена так:
при n=4,4 может быть получена так:
![]() (0 + 0)2+(,32)2+(-35 + 44)2+ (-70 + 64,988)2= 150,622,
(0 + 0)2+(,32)2+(-35 + 44)2+ (-70 + 64,988)2= 150,622,
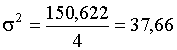 .
.
Таким образом, s = 6,14 дБ;
в) вычислим принимаемую мощность на расстоянии 2 км:
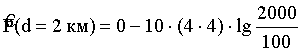 = -57,24 дБмВт.
= -57,24 дБмВт.
К полученному значению можно добавить возможное изменение этой величины с учетом Гауссового закона распределения вероятностей для учета случайных изменений величины принимаемой мощности;
г) вероятность того, что принятый сигнал на расстоянии 2 км будет больше -70 дБмВт, определяется из формулы ![]()
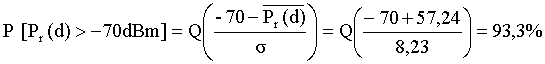 .
.
9. Решение:
Потери в свободном пространстве ![]() из формулы (5):
из формулы (5):
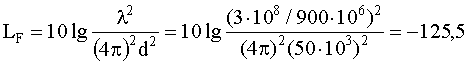 дБ.
дБ.
Из графиков Okumura (рис.13, 14) Ama (900 МГц, 50 км) = 43 дБ и GAREA = 9 дБ.
С использованием формулы (54а):
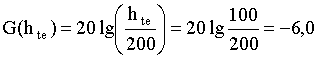 дБ;
дБ;
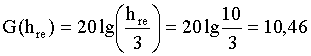 дБ.
дБ.
Из (53) общие средние потери в радиоканале:
![]() =
=
=-(-125,5) +,46 - 9 = 155,04 дБ.
Рэф = Pt Gt =![]() = 103 Вт.
= 103 Вт.
Рэф (дБ) = 10 lg Рэф = 30 дБВт = 60 дБмВт.
Средняя принятая мощность:
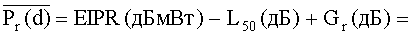
=60 дБмВт - 155,04 дБ+ 0 дБ = 95,04 дБмВт.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Грудинская радиоволн. М.: Высшая школа, 19с.
2. , Чернышев радиоволн. М.: Радио и связь, 19с.
3. Грудинская коротких и ультракоротких волн. М.: Радио и связь, 19с.
4. Сети телевизионного и звукового ОВЧ ЧМ вещания: Справочник/ Под ред. . М.: Радио и связь, 19с.
5. Walfisch J., Bertoni H. L. A theoretical model of UHF propagation in urban environments //IEEE Trans. on Antennas and Propagation. 1988. Vol. AP-36, № 10. P. .
6. Anderson J. B., Rappaport T. S., Yoshida S. Propagation measurements and models for wireless communications channels. //IEEE Communications Magazine. 1994. November.
ПРИЛОЖЕНИЕ
Параметры материалов на различных частотах
|
Материал |
Диэлектрическая проницаемость, er
|
Проводимость, s, См/м |
Частота, МГц |
|
Сухая земля |
4 |
0,001 |
100 |
|
Нормальная земля |
15 |
0,005 |
100 |
|
Влажная земля |
25 |
0,02 |
100 |
|
Морская вода |
81 |
5,0 |
100 |
|
Пресная вода |
81 |
0,01 |
100 |
|
Кирпич |
4,44 |
0,01 |
4000 |
|
Известняк |
7,51 |
0,028 |
4000 |
|
Стекло, 707 |
4 |
0, |
1 |
|
Стекло, 707 |
4 |
0,000027 |
100 |
|
Стекло, 707 |
4 |
0,005 |
10,000 |
РАСПРОСТРАНЕНИЕ РАДИОВОЛН
В МОБИЛЬНОЙ СВЯЗИ
Составители
Редактор
Подписано в печать 20.01.00 Формат 60х84 1/16
Бумага типографская Офсетная печать Усл. печ. л. 2,21
Уч.-изд. л. 1,49 Заказ 31 Цена "С"
Издательство УГТУ
Екатеринбург, Мира, 19




