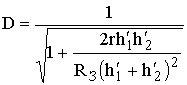.

Изменение напряженности поля волны при отражении от сферической поверхности можно рассчитать, используя следующие замены в интерференционных формулах для плоской Земли:

|Rсф| = D×|Rпл|, h¢1 = h1(1 - x2), h¢2 = h2(1 - x2), где .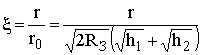

12. Распространение радиоволн в тропосфере

Тропосфера - приземной атмосферный слой, содержащий пары воды. Высота тропосферы: км в полярных зонах,км на средних широтах икм на экваторе. Газовый состав тропосферы постоянен и идентичен сос­таву у поверхности: 78% азота, 21% кислорода, 0,33% аргона, 0,03% CO2 и т. д. Содержание водяного пара - от 0 до 4% по объ­ёму.

Основные параметры тропосферы: p - общее давление, pc - давление сухого воздуха, абсолютная температура T, абсолютная влажность e (давление водяного пара). Температура в тропосфере с высотой h падает. Верхней границей тропосферы считается высота, на которой падение температуры прекращается (причина роста температуры с уменьшением высоты здесь - нагрев поверхности Земли).

При расчетах распространения радиоволн обычно используется модель "нормальной тропосферы" - гипотетической тропосферы, свойства которой отражают среднее состояние реальной тропосферы. "Нормальная тропосфера" имеет следующие параметры:

- pc(h = 0) = pc0 = 1013 мбар (1 бар=105 Па, 1 мм рт. ст. = 1,333 бар),

- T(h=0) = T0 = 2880K, T(h) = ,0065h[м],

- e(h=0) = 10 мбар, e(h) =,0035h[м],

- относительная влажность 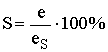= 60% (eS - давление насыщающих водяных паров) и не меняется с вы­сотой.

Коэффициент преломления n в тропосфере обычно определяется с помощью полуэмпирической формулы

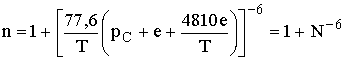, (12.1)

величину N = (n - 1)×106 в которой называют индексом преломления.

Локальные изменения давления, а также температурные инверсии приводят к колебаниям ко­эффициента преломления вблизи земной поверхности n = 1,00026 ¸ 1,00046. Выше 10 км полагают n = Const = 1,00011.

В силу поляризуемости молекул воздуха диэлектрическая проницаемость e (следовательно, и n) зависит и от частоты распространяющейся радиоволны, но этот эффект заметен лишь для волн c l < 10 см.

12.1. Атмосферная рефракция

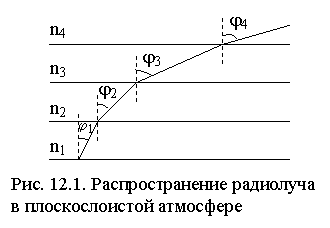Пусть радиоволна распространяется в плоскослоистой атмосфере (рис. 12.1). Согласно закону преломления

n1sinj1 = n2sinj2,

n2sinj2 = n3sinj3,

. . .

Таким образом, в слоистой атмосфере выполняется условие

n sinj = const (12.2)

Найдём радиус кривизны радиолуча в атмосфере. Пусть плоская волна, распространяясь в слое с коэффициентом преломления n под углом j, падает на слой толщиной dh с коэффициентом преломления n + dn (рис. 12.2). Проходя такой слой, она преломится и выйдет из него под углом j + dj. На участке AB траекторию волны можно представить отрезком кривой с радиусом r. Угол между касательными к кривой в точках A и B, а следовательно, и ÐAOB, равен dj. Радиус кривизны траектории 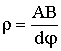. 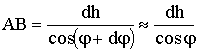Но , тогда

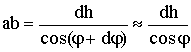. (12.3)

Продифференцируем (12.2): d(n×sinj) = dn×sinj + n×cosj×dj = 0,

откуда

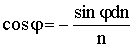. (12.4)

Подставим (12.4) в (12.3):

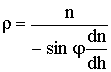. (12..5)

Поскольку радиотрассы обычно можно считать пологими, т. е. sinj » 1, и, кроме того, в тропосфере n » 1, из (12.5) получаем

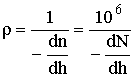. (12.6)

Если коэффициент преломления меняется с высотой по линейному закону, то ра­диус кривизны траектории с высотой не меняется, т. е. имеем распространение по дуге ок­ружности. Для модели нормальной тропосферы м-1 , следовательно, r » 25000 км » 4RЗ. Распространение радиоволн по дуге круга такого радиуса называется нормальной тропосферной рефракцией.

12.2. «Эквивалентный» радиус Земли

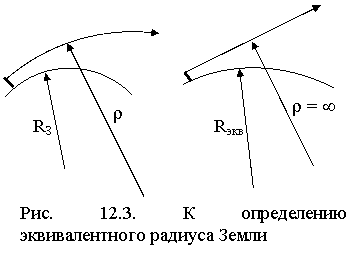Для учета тропосферной рефракции радиоволн в полученных ранее выражениях можно свести реальную криволинейную траекторию радиоволны к прямолинейной, при этом радиус Земли RЗ заменяется эквивалентным радиусом Rэкв. Рассмотрим две схемы (рис. 12.3). Они эквивалентны, если относительная кривизна между лучом и поверхностью в обоих случаях одинакова, т. е. выполняется равенство

,

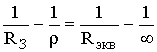откуда, используя 12.6, получаем

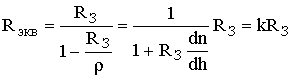. (12.7)

Для нормальной тропосферы k » 4/3, следовательно, Rэкв » 8500 км.

Таким образом, тропосферную рефракцию можно учесть, заменяя в формулах для прямолинейного распространения RЗ на Rэкв. Например, расстояние прямой видимости между антеннами изменится следующим образом

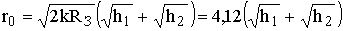, км.

Отметим, что введение Rэкв указанным выше способом справедливо, если коэффициент преломления меняется с высотой по линейному закону.

12.3. Виды атмосферной рефракции

Из (12.1) и параметров нормальной тропосферы следует, что вблизи земной поверхности

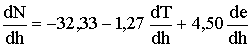. (12.8)

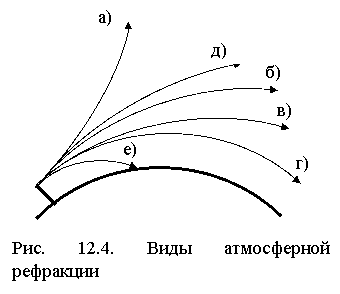
1. Отрицательная рефракция (рис. 12.4а). Соответствует случаю . Согласно (12.5), при этом r < 0, т. е. траектория волны направлена вы­пуклостью вниз. Из (12.8) следует, что такой вид рефракции возможен при , . Наблюдается в континентальных районах с умеренным клима­том, осенью и весной во время утренних туманов. Наземная связь ухудшается по сравнению с нормальной.

2. Положительная рефракция: , следовательно, r > 0, т. е. траектория радиолуча обращена выпуклостью вверх. Различают следующие частные случаи:

а) нормальная рефракция (рис. 12.4б): , , следовательно, = -4×10-8 м-1, Rэкв = 8500 км, r = 25000 км, k = 4/3. Наиболее распространённый вид положительной рефракции. Чаще наблюдается в дневные ча­сы;

б) повышенная рефракция (рис. 12.4в): , , 8500 км < Rэкв < ¥, - 15,7×10-8 м-1 < < - 4×10-8 м-1. Наблюдается в континентальных районах средних широт в вечерние, ночные и утренние часы летом вследствие тем­пературных инверсий и резкого уменьшения влажности с высотой;

в) критическая рефракция (рис. 12.4г). Радиолуч движется параллельно поверхности Земли на постоянной высоте. Rэкв = ¥ , r = RЗ, т. е. должно быть 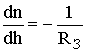= -15,7×10-8 м-1. Условия возникновения - как и для пункта б);

г) пониженная рефракция (рис. 12.4д): , , RЗ < Rэкв < 8500 км, -4×10-8 м-1 < < 0. Температура с высотой убывает быстрее, а влажность - медленнее, чем при нормальной рефракции. Обычно наблюдается в пасмурную, дождливую погоду. Дальность радиосвязи меньше, чем при нормальной рефракции.

3. Сверхрефракция (волноводная рефракция) (рис. 12.4е): , , < -- 1/Rэкв, r < RЗ, Rэкв < 0. В этом случае волна, отразившись от области высокого градиента, достигает поверхности Земли, отражается от нее, снова преломляется в тропосфере и т. д., так появляется тропосферный волновод. Условия появления: резкое понижение n с высотой обычно вследствие температурной инверсии как вблизи поверхности, так и на вы­сотах 2 - 3 км. Поскольку температурные инверсии наблюдаются нерегулярно, можно прог­нозировать только вероятность появления волновода в определённом районе в определённое время. Появление сверхрефракции над значительным участком земной поверхности способствует дальнему распространению дм и см волн. Вертикальный размер атмосферного волновода >> длины волны, которая может быть им захвачена. Максимальная длина волны, которая еще может быть захвачена волноводом с вертикальным размером h0, определяется соотношением /1/

lmax = 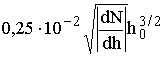, м.

Например, над поверхностью моря » 0,1, тогда lmax » 8,5×10-4h03/2 и предельные длины захватываемых волн для некоторых h0 следующие:

Необходимая для сверхрефракции температурная инверсия может одновременно иметь место как в приземном слое, так и в слоях на некоторой высоте, и тогда возникают условия возникновения приподнятого волновода, в котором захва­ченная волна распространяется, отражаясь от верхнего и нижнего инверсионных слоев. Возможно одновременное существование и приземного, и приподнятого волново­дов. Исследования показывают, что приподнятые инверсионные слои появляются на высо­тах от 5 до 3000 м. Толщина таких слоев от нескольких м до 100 м. Перепад Dn составляет » 5×10-5. В таких условиях коэффициент отражения имеет достаточную вели­чину только для самых пологих волн (обычно угол возвышения луча не должен превышать 0,50) и при малой толщине слоя в масштабах l. Путем отражения от таких слоев возможно распространение радиоволн на расстояния до км. Ре­гулярная связь невозможна ввиду непостоянства слоев. Часто возникают условия многолучевого распространения, когда в точку приема приходят волны, отра­женные от верхнего слоя, а также отраженные от нижнего слоя или от земной поверхности. Поскольку атмосферные слои движутся, длина пути интерференционных лучей будет непрерывно меняться, что приводит к быстрым колебаниям напряжённости принимаемого сигнала.

12.4. Флуктуации радиосигнала и многолучевость распространения

Флуктуации - случайные, хаотического порядка, отклонения рассматриваемой величины от ее среднего значения. В радиоканале обычно флуктуируют амплитуда и фаза принимаемого сигна­ла. Причины флуктуаций радиосигнала:

1) определённые изменения во времени свойств среды распространения;

2) многолучевость в процессе распространения.

Многолучёвость бывает дискретной и диффузной. Пример дискретной многолучёвости. Пусть в тропосфере на высоте h сформировался инверсионный слой - область резкого изменения n с высотой, от которого может отразиться радиолуч (рис. 12.5). Тогда в точку приема В, помимо прямого луча 1, попадает и луч 2, отразившийся от инверсионного слоя. Если луч 1 создает в точке В поле , а луч 2 - поле , где Dr - разность хода лучей, то амплитуда напряжённости поля в точке приёма

.

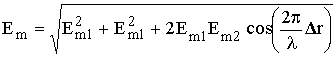Поскольку область инверсии реально непрерывно меняет свою форму и высоту (за счет вертикальных и горизонтальных потоков воздуха), Dr также будет непрерывно менять­ся. Если разность хода такова, что 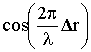® -1,то величина Em ® Em1 - Em2 и может быть близка к нулю, если Em1, Em2 одного порядка величины. При 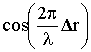® 1 результирующее поле Em ® Em1 + Em2, т. е. растет. Пусть AB = 300 км, h = 5 км, l = 4 см, тогда при вертикальном перемещении области отражения со скоростью v = 0,6 м/с время изменения резуль­тирующего поля от максимального до минимального значений Dt = 1 с. Таким образом, будут наблюдаться замирания принимаемого сигнала с частотой f = 1/ Dt = 1 Гц.

Пример диффузной многолучёвости. Пусть случайные неоднородности коэффициента преломления n перемещаются ветром поперек трассы (рис. 12.6). В результате, на пути АВ радиоволны оказываются все новые и новые неоднородности n различной конфигура­ции. Поскольку в тропосфере величина случайных флуктуаций Dn » (1 ¸ 2)10-6, на амплитуду принимаемого сигнала они существенно не влияют, однако может заметно изменяться фаза сигнала

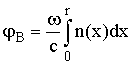, (12.9)

где r - путь, проходимый волной в неоднородной среде. Здесь мы имеем дело с диффузной многолучевостью, когда поле в точке приема создается множеством вторичных источников на поверхности фронта волны, фазы каждого из которых изменяются согласно (12.9). А так как пересекаемый поток непрерывно меняется по составу неоднородностей, ко­нечный интерференционный сигнал будет непрерывно флуктуировать.

Методы борьбы с замираниями сигнала, обусловленными многолучевостью:

1) пространственный разнос, т. е. одновременный прием на две антенны, разнесённые перпендикулярно трассе на расстояние L = (70 ¸ 100)l,

2) частотный разнос, т. е. одновременный приём на двух частотах, разнесённых на Df. Теория и практика показывают, что Df должна отвечать соотношению (2 ¸ 5)×10-3.

12.5. Рассеяние УКВ на турбулентных неоднородностях

При достижении определенной скорости упорядоченное, ламинарное движение воздушных масс (при котором один слой газа движется относительно другого с определённой скоростью) нарушается, и возникает вихревое, турбулентное движение. О характере движения можно судить по величине числа Рейнольдса

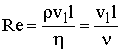, (12.10)

здесь r - плотность газа, l - характерный масштаб некоторого объема движущейся среды, vl - ско­рость его перемещения, h - коэффициент динамической вязкости, n - коэффициент кинематической вязкости.

Если число Re больше некоторого критического значения Reкр, движение становится турбулентным. Основные закономерности такого движения известны благодаря работам Колмогорова и Обухова. Если в турбулизованной среде возникает вихрь масштаба l такого, что соответствующее ему число Re >> Reкр, то он неустойчив, быстро разрушается, и на его месте возникают вихри масштаба l' < l. В случае выполнения и для этих вихрей ус­ловия Re > Reкр, они также разрушаются и т. д. до тех пор, пока для некоторого масштаба l0 не получим < Reкр. Неоднородности масштаба l < l0 исчезают под действием сил вяз­кости, кинетическая энергия вихрей переходит в тепловую. Масштаб l0 называется внутренним масштабом турбулентности. В тропосфере l0 » нескольким мм. Таким образом, в турбулентной атмосфере существует целый спектр масштабов l турбулентных неодно­родностей скорости ветра от l0 до максимального масштаба турбулентности L (в тропосфере L » 50 ¸ 100 м).

Благодаря турбулентному движению различ­ные элементы объема воздуха могут переноситься из одной области пространства в другую почти без изменения своих параметров. В результате, в каждой точке тур­булизованной среды имеются флуктуации давления, плотности, тем­пературы, что приводит к пульсациям коэффициента преломления n. В тропосфере турбулентные флуктуации Dn » (1 ¸ 2)10-6.

Турбулентные флуктуации n вызывают рассеяние радиоволн, характер которого зависит от соотношения между размером неоднородностей l и длиной волны l. Если l >> l, неоднородности действуют как оптическая линза: максимум переизлучения в направлении первоначального распространения, и чем больше отношение l / l, тем ýже диаг­рамма направленности. Однако рассеяние будет наблюдаться и по другим направлениям.

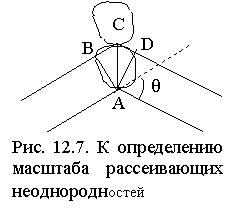Рассмотрим наземную радиотрассу и выясним условия, наиболее благоприятные для приема рассеянного сигнала. Пусть AC = l - расстояние между рассеивающими неоднородностями по вертикали (рис. 12.7). В точке приема волны от вторичных источников А и С интерферируют, максимум сигнала полу­чится при совпадении этих волн по фазе, для чего разность хода лучей

,

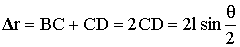должна быть равна (кратна) l, откуда получаем связь между углом рассеяния q и минимальным размером рассеивающих неоднородностей l:

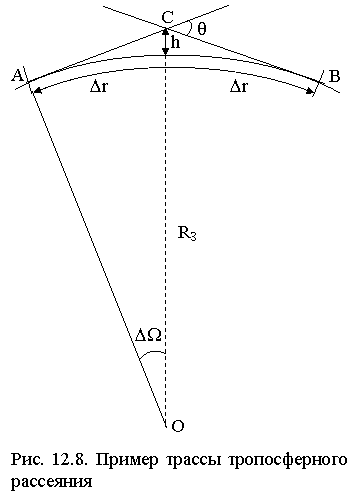
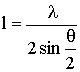. (12.11)

Таким образом, рассеянный сигнал в точке приема формируется определенными масштабами турбулентных неоднородностей, т. е. рассеяние носит селектив­ный характер. Для трасс, использующих тропосферное рассеяние, характерны следующие параметры:

- высота пересечения главных максимумов диаграмм направленности 3 ¸ 5 км, что обеспечи­вает связь на расстояниях до 900 км;

- мощность передатчика Р0 = 10 ¸ 100 кВт, ширина диаграмм направленности не более 10 (обеспечивается параболическими антеннами диаметром до 40 м), что обусловлено большими потерями энергии при рассеянии;

- рабочая полоса частот 300 ¸ 5000 МГц определяется как спектром наблюдающихся масштабов неоднородностей, так и тем, что на больших частотах сильно растут потери энергии, а на более низких требуют­ся большие антенны.

Пример трассы тропосферного рассеяния (рис. 12.8). Пусть передающая (A) и приёмная (B) антенны направлены на горизонт, и высота пересечения главных максимумов диаграмм направленности над серединой трассы h = 5 км. Найдём угол рассеяния q, полагая RЗ = 6378 км. Из DOAC имеем 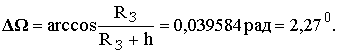Тогда q = 2DW = 4,540.

AC =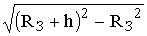= 252,6 км, Dr = RЗ×DW = 6378×0,039584 = 252,46 км, следовательно, расстояние между концами трассы ÇAB = 2Dr » 505 км. Если предположить, что рассеяние эффективно на масштабах неоднородностей, не превышающих 10 м, то на данной трассе следует использовать радиоволны с l < 20×sin2,270 = 0,79 м, т. е. частоты f > 380 МГц.

12.6. Полоса пропускания тропосферного канала

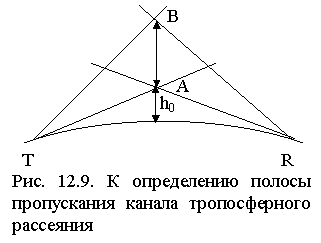Рассеяние по своей природе многолучевый процесс, поэтому сигнал в точке приема будет флуктуировать, что ограничивает, например, полосу Df пропускания тропосферного канала. Оценим Df. Пусть точку приема достигают как лучи, рассеянные самой низкой точкой рассеивающего объема Vрасс (т. A), так и лучи от самой высокой точки рассеяния (т. B) (рис. 12.9). Между лучами, распространяющимися по этим крайним путям, существует разность хода Dr. Сдвиг фаз Dj на различных частотах для одного и того же пути будет различен. На несущей частоте f

,

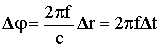где Dr = TBR - TAR. На крайней боковой частоте fn » f + Fn сдвиг фаз изменится до величины

.

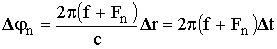Таким образом, в один и тот же момент времени на разных частотах напряженность полей волн складывается в разных фазах. Для минимизации искажений необходимо, чтобы разность

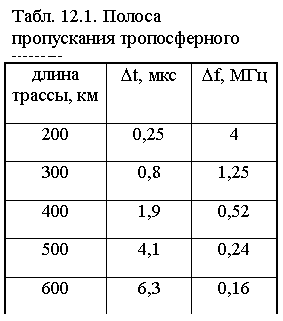Dj - Djn = 2pFnDt << 2p,

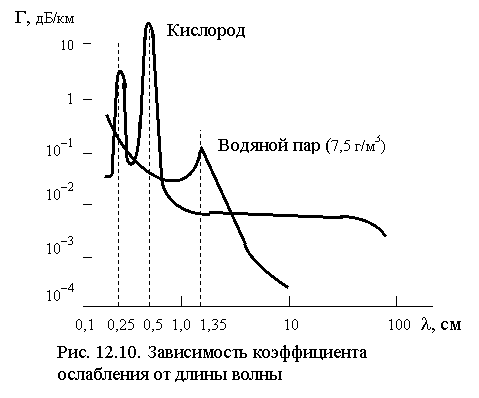
следовательно, Fn << . Примерные значения полосы пропускания для раз­личных тропосферных трасс при условии AB » 3h0 приведены в табл. 12.1.

Суточный ход тропосферного рассеянного сигнала практически не выражен, в сезонном ходе имеются летний максимум и зимний минимум, обусловленные измене­нием метеоусловий.

12.7. Поглощение радиоволн в тропосфере

Основной причиной поглощения в тропосфере является селективное или резонансное поглощение молекулами газов (N2, O2, H2O) и поглощение в каплях воды. Резонансное поглощение обусловлено усилением взаимодействия радиоволн с молекулой при совпадении их частот с частотой внутриатомного движения электронов внешних орбит. Резонансные линии всех газов тропосферы, за исключением кислорода и водяного пара, расположены вне радиодиапазона. При распространении в поглощающей среде амплитуда напряжённости поля радиоволны уменьшается по закону Em(r) = E0me-a×r (E0m - начальная амплитуда, a - коэффициент затухания).

На рис. 12.10 приведена зависимость коэффициента ослабления Г, определяемого здесь как

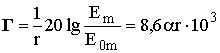[дБ / км],

от длины волны для O2 и паров H2O. У кислорода в радиодиапазоне имеются две резонансные линии: при l = 0,5 см Г = 14 дБ / км и при l = 0,25 см Г = 3,5 дБ / км. У водяного пара резонансное поглощение имеет место при l = 1,35 см. Зависимость поглощения от удельной влажности линейна: чем выше влажность, тем выше пог­лощение.

Поглощение радиоволн с l < 1 см тропосферными газами настолько велико, что они могут быть использованы для радиосвязи лишь на весьма короткие расстояния.

Капельковые образования (гидрометеоры - дождь, туман, снег) могут вызвать заметное поглощение радиоволн с l < 3 см, потому что, во-первых, радиоволны наводят в каплях токи смещения, и часть их энергии переходит в джоуле­во тепло. Во-вторых, токи являются источником вторичного излучения, что приводит к рассеянию энергии радиоволн. Затухание растет с уменьшением l, ростом размеров капель и интенсивности осадков. Рассеяние см радиоволн гидрометеорами ведет к появлению отраженных сиг­налов, мешающих нормальной работе РЛС.

13. Распространение радиоволн в ионосфере

13.1 Образование и строение ионосферы

Ионосфера - область атмосферы, в которой газ частично ионизирован, так что присутствуют свободные электроны и ионы. Основные причины ионизации - фотоионизация и ударная ионизация. Фо­тоионизация наблюдается под влиянием излучения с частотой выше некоторого значения, если энергия кванта этих колебаний превышает работу иони­зации. Ударная ионизация вызывается попаданием в атмосферу частиц, обладающих достаточным запасом кинетической энергии. Основным источником ионизации является Солнце, постоянно излучающее потоки электромагнитного и корпускулярного излучения. Поверхности Земли достигают ультрафиолетовые лучи (УФЛ) с l > 2900 Å. Более короткие поглощаются в атмосфере, вызывая диссоциацию молекул, образо­вание ионов озона и т. д. Ионизация вызывается УФЛ с l < 1000 Å, мягким рентгеновским излучением с l = 10 ¸ 300 Å и солнечным корпускулярным излучением. В ночное время основной причиной ионизации являются: излучение звезд, составляющее примерно 0,001 от солнечного, космические лучи, ионизирующие нижние слои атмосферы (до 10-8 ионизирующего излучения Солнца). Степень ионизации в высоких слоях резко возрастает во время солнечных вспышек. Степень ионизации максимальна на высоте, где достаточно велика плот­ность атмосферы и еще не слишком ослаблен поток ионизирующих частиц и волн.

При моделировании ионосферы часто используется приближение параболического слоя, согласно которому вертикальный профиль электронной концентрации N(h) описывается выражением

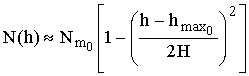, (13.1)

(H - полутолщина слоя), хорошо аппроксимирующим высотное изменение электронной концентрации ниже максимума Nm (рис. 13.1). В приближении изотермической атмосферы Nm соответствует высоте » 300 км.

Реальная атмосфера: 1) не изотермична; 2) неоднородна по составу, на высотах > 100 км начинается ее расслоение. 3) характеризуется несколькими высотными максимумами ионизации, каждому из которых соответствует свой слой.

Образование слоя D (h =км) связывают с амби­полярной диффузией ионов из слоя E до высот, на которых постоянная времени рекомбинации еще достаточно велика. Ночью диффузия уменьшается, и слой D пропадает.

Слой E с высотой максимума ионизации » 120 км обязан своим существованием диссипации молекул O2 рентгеновским излу­чением и УФЛ Солнца. Суточный и сезонный ход NE ~ cos z, где z - зенитный угол Солнца.

Слой F1 связан с ионизацией молекул N2, имеющей максимум на высотах h = 180 ¸ 240 км. Существует только летом и днем, NF ~ cos z.

Слой F2 имеет максимум на высотах 250 ¸ 350 км, что соответствует максимуму ионизации атомарного кислорода O.

Степень ионизации ионосферных слоев испытывает четко выраженные регулярные суточные, сезонные и 11-летние вариации. Кроме регулярных процессов существует множество других (например, турбулентность), приводящих к случайным колебаниям степени иониза­ции, возникновению локальных неоднородностей электронной концентрации.

13.2. Преломление радиоволн в ионосфере

Так как масса электрона в 1836 раз меньше массы протона, основное влияние на распространение радиоволн в ионосфере оказывают электроны. На электрон в поле радиоволны действует пере­менное электрическое поле напряженностью

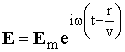. (13.2)

[ю1]  Если в единице объема содержится N электронов, то под воздействием силы возникает направленное перемещение электронов - конвекционный ток плотностью

jэл = evN, (13.3)

где v - скорость движения электронов, e = 1,602×10-19К - заряд электрона.

Рассмотрим уравнение движения электрона

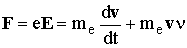(13.4)

(me = 9,106×10-31 кг - масса электрона, n - частота столкновения электрона с ионами, атомами, молекулами воздуха в единицу време­ни, после каждого из которых он теряет количество движения mev), согласно которому действующая на заряд электрическая сила уравновешивается силой инерции частицы и силой трения. Считая поле волны гармоническим, будем искать решение (13.4) в виде

. (13.5)

Подставляя (13.5) в (13.4), получаем

,

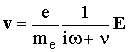следовательно, согласно (13.3),

.

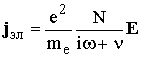Поскольку ток смещения имеет плотность , плотность результирующего тока

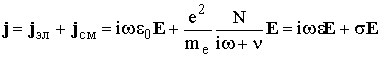. (13.6)

Приравняв в (13.6) действительную и мнимую части, нетрудно получить

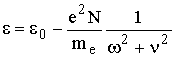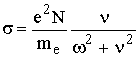, . (13.7)

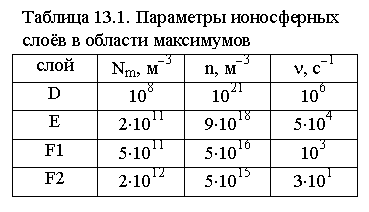Частота столкновений электрона n = nen + nei (nen, nei – частоты столкновений с нейтральными частицами и с ионами соответственно). Для ионосферы характерны параметры, приведенные в табл. 13.1. Отметим, что концентрации нейтральных и заряженных частиц сравниваются на высотах 800 – 1000 км. Ниже 500 км n >> N, и можно полагать n »nen. В ионосферу проникают радиоволны короче СВ, т. е. с частотами f > 3 Мгц = 3×106 Гц. Из табл. 13.1 следует, что для таких радиоволн w2 = (2pf)2 >> n2, поэтому (13.7) можно упростить:

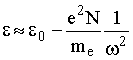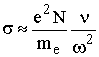, . (13.8)

Тогда e¢ можно представить в виде

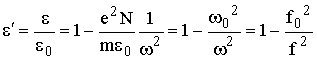. (13.9)

Введённые в (13.9) параметры 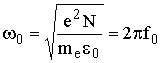и 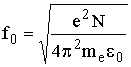называются плазменными частотами. Подставив значения e, me, e0, получаем 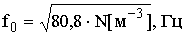. Таким образом, можно записать

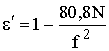. (13.10)

Если в тропосфере e¢ > 1 и отличается от единицы где-то в 4-м знаке после запятой, то в ионосфере e¢ < 1 и может меняться в широких пределах. Поскольку

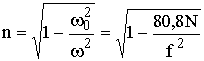, (13.11)

то и скорость распространения волны является функцией частоты, следовательно, ионосфера является диспергирующей средой. В такой среде по мере распространения возникают фазовые искажения немонохроматического сигнала. Для монохроматической волны набег фазы после прохождения пути r

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4