3. Шкала коэффициентов риска.
Помимо коэффициентных показателей для оценки риска отдельных операций или групп операций, прежде всего банковских, широко используют шкалы коэффициентов риска. При использовании шкал риска отдельным операциям присваивают определенный коэффициент риска, значение которого определяется, как правило, на основе статистических данных.
Применительно к практике банковского дела в России активы коммерческого банка по степени риска подразделяются на 5 групп, которым присваиваются дополнительно соответствующие поправочные коэффициенты.
Таблица 3
Шкала коэффициентов риска
Активы
Коэффициент риска, %
1 группа.
Средства на корреспондентском и на резервном счете в ЦБ
Вложения в государственные долговые обязательства
Касса и приравненные к ней средства
0
0
2
2 группа.
Ссуды, гарантированные Правительством РФ
Ссуды под залог государственных ценных бумаг РФ
10
10
3 группа.
Вложения в долговые обязательства субъектов РФ
Средства на корреспондентских счетах у банков-неризидентов
Ссуды под залог ценных бумаг субъектов РФ
20
20
20
4 группа.
Средства на счетах у банков-резидентов
Ценные бумаги для передачи
Собственные здания и сооружения за минусом переданных в залог
70
70
70
5 группа.
Все прочие активы кредитной организации
Гарантии, поручительства, выданные кредитной организацией
100
50
Этот же метод используется для определения индексов опасности, когда необходимо оценить потенциальную опасность промышленных объектов, если требуется оценить риск интегрально, не вдаваясь в детали производственных процессов. Оценка производится числовым значением (индексом). Например, при оценке пожаро - и взрывоопасности используется метод индекса Дау (Dow Fire and Explosion Index).
Опосредованная оценка риска на основе относительных показателей
Технология оценки риска построена на расчете финансовых показателей различного состава и предназначения и сравнении фактических результатов с рекомендуемыми (нормативными) значениями. Часто в ходе анализа показатели рассчитываются на начало и конец отчетного периода. Если фактическое значение показателя не соответствует рекомендациям (требованиям), то целесообразно оценить его динамику (увеличение или снижение значения). Как правило, для оценки конкретного вида риска (например, риска потери ликвидности или платежеспособности) используется группа показателей, каждый из которых характеризует отдельные формы проявления риска, и для оценки риска в целом эти показатели «сворачивают» в обобщенную оценку на основе специально разработанных моделей и правил оценки. Расчетные модели для определения этих коэффициентов и рекомендуемые значения содержаться в пособиях по финансовому анализу.
Рассмотрим опосредованную оценку риска на основе методики оценки риска потери платежеспособности.
Данная оценка осуществляется на основе различных коэффициентов ликвидности, которые учитывают набор и относительные доли активов различных групп, рассматриваемых в качестве покрытия наиболее срочных обязательств и краткосрочных пассивов. Состав коэффициентов ликвидности, их физическое содержание и нормативные требования к ним приведены в таблице 4.
Таблица 4
Финансовые коэффициенты ликвидности (платежеспособности)
№ п/п
Показатель
Способ расчета
Ограничение
Примечание
1
Общий показатель платежеспособности
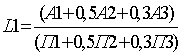
≥ 1
-
2
Коэффициент абсолютной ликвидности
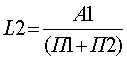
> 0,2-0,7
Показывает, какую часть краткосрочной задолженности предприятие может погасить в ближайшее время за счет денежных средств и краткосрочных ценных бумаг
3
Коэффициент «критической оценки»
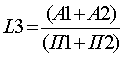
Допустимое значение 0,7-0,8
желательно ≥1,5
Показывает, какая часть краткосрочных обязательств предприятия может быть немедленно погашена за счет средств предприятия на различных счетах, в краткосрочных ценных бумагах, а также поступлений по расчетам с кредиторами
4
Коэффициент текущей ликвидности
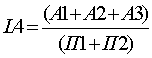
Необходимое значение – 1, оптимальное – не менее 2,0
Показывает, какую часть текущих обязательств по кредитам и расчетам можно погасить, мобилизовав все оборотные средства
5
Коэффициент маневренности функционирующего капитала
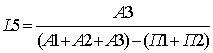
Уменьшение показателя в динамике - положительный факт
Показывает, какая часть функционирующего капитала обездвижена в производственных запасах и долгосрочной дебиторской задолженности
6
Доля оборотных средств в активах
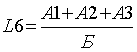
≥0,5
Зависит от отраслевой принадлежности
2.3. Показатели риска в условиях частичной неопределенности:
вероятностные и статистические показатели оценки риска
2.3.1. Вероятностные показатели оценки риска
Условия частичной неопределенности (риска) – условия, когда известны возможные варианты развития событий, прогнозируемые значения необходимых показателей и величин хозяйственной деятельности, а информация о рисковой ситуации существует в виде частот проявления рисковых событий (вероятностей).
В этом случае существует возможность оперирования данными для оценки риска с учетом вероятностного характера событий реальной экономической ситуации.
Как известно, риск имеет вероятностную природу, то есть в процессе предпринимательской деятельности рисковое событие может произойти, а может и не произойти. Тем самым риск определяется как вероятностная категория - некоторое событие, мерой которого может быть вероятность, характеризующая его уровень. Величина этой вероятности определяется действием как внешних, так и внутренних факторов риска, однако вероятностная природа риска остается его постоянной характеристикой.
Для оценки риска в условиях частичной неопределенности могут использоваться вероятностные и статистические показатели.
Вероятностные оценки показателей риска рассчитываются на основе классических принципов статистической вероятности с использованием стохастических моделей. Формой выражения данных показателей являются точечные и интервальные оценки последствий риска.
Исходная информация в данном случае существует в виде частот проявления рисковых событий.
Вероятностные оценки риска могут быть точечными и интервальными.
1. Точечная оценка риска
В данном случае при оценке риска исходят из предположения, что результат деятельности (как случайная величина) подчинен нормальному или близкому к нормальному закону распределения.
Кривая функции плотности нормального распределения представляет собой графическое изображение зависимости плотности распределения вероятностей возможных значений результатов деятельности (рис.9)
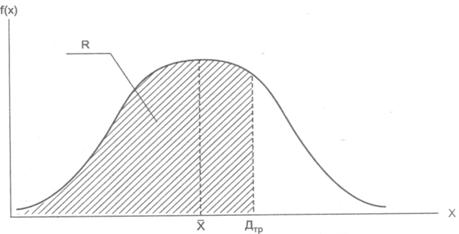
Рис. 9 Кривая плотности нормального распределения.
На практике точечная оценка риска предполагает построение кривой риска и определение характерных точек. Однако для использования данного метода требуется достаточно объемный массив статистических данных, чтобы проверить статистические гипотезы о виде и параметрах закона распределения.
Обычно определение вероятностных показателей основано на определении частоты и частости. Частота событий характеризует, насколько часто встречаются те или иные значения результата в распределении. Частость представляет собой частоту, выраженную в долях единицы или процентах к итогу.
Так, если установлено, что некоторый i-тый результат происходит в ni случаях из N, то его частота равна:
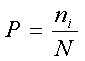(4)
Частость равна:
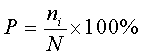. (5)
Если число наблюдений велико, что частость результата при первом приближении может быть принята за его вероятность. Естественно, что сумма вероятностей равна единице.
Например, данные расчета вероятности норм прибыли могут быть представлены следующим образом (таблице 5):
Таблица 5
Статистические данные о норме прибыльности проекта
Норма прибыли на капиталовложения, %
Частота результатов
Частость результатов, %
Кумулятивная величина вероятностей
30-40
5
5
5
20-30
19
19
24
10-20
33
33
57
0-10
21
21
78
-10-0
14
14
92
-20-10
8
8
100
Всего
100
100
-
Распределение вероятностей можно представить графически в виде гистограммы.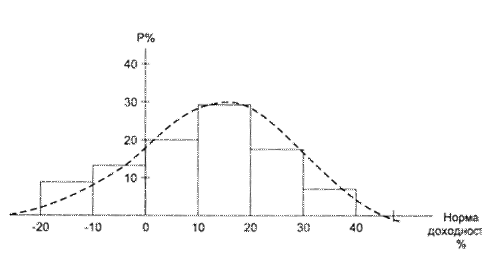 
Рис. 10 Гистограмма распределения капиталовложения по нормам прибыли
Исходя из кривой распределения возможных значений результатов деятельности возможно построение кривой риска (обычно в другой системе координат), которая дает наглядное представление о возможностях получения прибыли и опасности возникновения потерь.
Для определения вероятности негативного отклонения результата и уточнения оценок риска вероятностные показатели могут быть взаимосвязаны с коэффициентными показателями или входить в конструкцию комплексных показателей для учета стохастичности предпринимательской среды.
Вероятностная оценка риска также может иметь вид различных коэффициентов.
Например, экономический риск (характеризующий вероятности технического и коммерческого успеха) может быть рассчитан по американской методике оценки технических нововведений. Ценным в нем является стремление учесть вероятностный характер ожидаемого результата в условиях неопределенности, все затраты и весь ожидаемый эффект. Американские компании используют для определения эффективности реализации нововведений:
Э = (П × С × Т × Рт × Рк) / Ез, (6)
где Э – эффективность реализации нововведений;
П – ежегодный объем продажи нового изделия;
Т – жизненный цикл новшества;
Рт – вероятность технического успеха;
Рк – вероятность коммерческого успеха;
Ез – сумма затрат на реализацию.
2. Интервальная оценка риска
Часто предпринимателю, оценивающему риск своей деятельности, необходимо определить вероятность получения результата в заданных пределах.
Одной из наиболее известных методов интервальной оценки риска является концепция рисковой стоимости VaR (Value at Risk), разработанная в конце 80-х годов.
VaR является универсальной методикой расчёта различных видов риска:
- ценового риска - риска изменения стоимости цены финансового актива на рынке;
- валютного риска - риска, связанного с изменением рыночного валютного курса национальной валюты к валюте другой страны;
- кредитного риска - риска, возникающего при частичной или полной неплатёжеспособности заёмщика по взятому кредиту;
- риска ликвидности - риска, связанного с невозможностью продажи финансового актива, либо реализации с большими убытками, возникающими при продаже актива в силу большой разницы величины покупки/продажи, существующей на рынке.
Методология VaR обладает рядом несомненных преимуществ: она позволяет измерить риск в терминах возможных потерь, соотнесенных с вероятностями их возникновения; позволяет измерить риски на различных рынках; позволяет агрегировать риски отдельных позиций в единую величину для всего портфеля и т. д.
VaR является суммарной мерой риска, способной производить сравнение риска по различным портфелям (например, по портфелям из акций и облигаций) и по различным финансовым инструментам (например, форварды и опционы).
Упрощенная методика расчета VaR следующая.
Для начала нужно определить логарифмы однодневных изменений курсов акций для каждой позиции по формуле:
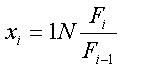(7)
где F - курс акции на i-тую дату;
Затем рассчитывается стандартное отклонение для каждой позиции:
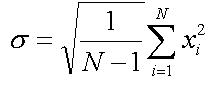(8)
где N - количество дней.
При расчете значения VaR на период более одного дня данное выражение умножается еще и на корень их числа дней, на которое рассчитывается VaR.
После этого уже рассчитывается сам показатель VaR по формуле:
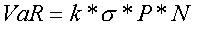(9)
где k - коэффициент, соответствующий каждому из доверительных уровней 90%, 95%, 97,5% и 99%;
P - текущая стоимость финансового инструмента;
N - количество финансовых инструментов данной позиции. Обычно расчет VaR производится для доверительных уровней 90%, 95%, 97,5% и 99%.
Коэффициенты, соответствующие каждому из доверительных уровней, приведены в таблице:
Таблица 6
Доверительные уровни для расчета показателя VaR
Доверительный уровень
Коэффициент
90,0 %
1,28
95 %
1,65
97,5 %
1,96
99,0 %
2,33
В настоящее время использование данной методики производится с помощью специализированных программ.
2.3.2. Статистические показатели оценки риска
Статистические показатели оценки риска по своей информативности несколько уступают вероятностным, но требуют меньшего объема исходной информации для оценки уровня риска.
В качестве статистических показателей используют средние показатели значения результатов деятельности и показатели колеблемости полученного результата.
Средние значения результатов деятельности
Для дискретных случайных величин для оценки риска используется среднее ожидаемое значение, которое рассчитывается как средневзвешенное произведение всех возможных значений результатов на вероятности их возникновения.
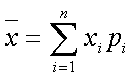, (10)
- абсолютное значение i-того события или результата,
- вероятность наступления i-того события или результата,
n – число вариантов исходов события.
В реальной экономической действительности чаще всего приходится иметь дело со статистическими аналогами случайных величин, которые определяются выборочным путем. Тогда определяется выборочная средняя:
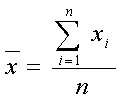, (11)
В данном случае выборочные характеристики случайных величин при достаточно большом количестве наблюдений могут быть принятыми приближенно равными вероятностям этих случайных величин.
Использование средних величин для оценки риска позволяет оценить обобщенную количественную характеристику, но для принятия решения необходимо оценить колеблемость результата относительно варианта относительно среднего значения. Для этого используют показатели вариации уровня риска.
Показатели вариации уровня риска
1. Наиболее простой формой статистического показателя, характеризующего риск, является показатель размаха вариации ожидаемого результата.
Показатель размаха вариации – учитывает отклонение крайних значений результата от среднего.
, (12)
где Xmax, Xmin – соответственно наибольшее и наименьшее значения результата в выборочном наблюдении.
Точнее вариацию результата характеризуют статистические показатели риска, учитывающие значимость колеблемости всех возможных значений результата от среднего ожидаемого состояния.
В настоящее время распространена точка зрения, согласно которой мерой риска результата решения следует считать дисперсию, среднее квадратическое отклонение (стандартное отклонение), коэффициент вариации.
2. Дисперсия как показатель степени риска для дискретных случайных величин представляет собой средневзвешенную величину из квадратных отклонений действительных результатов от средних ожидаемых.
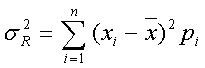, (13)
где – i-тое значение случайной величины;
– вероятность того, что случайная величина примет значение .
3. Среднее квадратическое отклонение является именованной величиной и указывается в тех же единицах, в каких изменяется варьирующий признак.
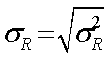, (14)
Статистическими аналогами приведенных характеристик, определяемых выборочным путем, являются выборочная дисперсия, выборочное среднее квадратическое отклонение, формулы для которых будут иметь следующий вид:
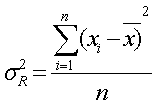, (15)
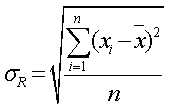, (16)
При увеличении числа наблюдений очевидно, что все статистические характеристики будут сходиться по вероятности к соответствующим математическим характеристикам и при достаточном количестве n могут быть приняты приближенно равными им.
Таким образом, поскольку риск обусловлен случайностью принятого решения, то чем меньше разброс (дисперсия) результата решения, тем более он предсказуем и тем меньше его величина. Если дисперсия равна нулю, риск полностью отсутствует.
Например, изобразим 2 кривые распределения, имеющие одинаковые средние значения результатов, но различающиеся величиной дисперсии (рис.11). Очевидно, что второй результат более рискованный.
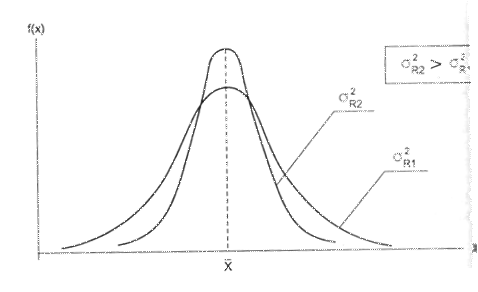
Рис. 11 Дисперсии распределения результата принятого решения
4. Если необходимо сравнить варианты решений с разными средними значениями результата и разными средними квадратическими отклонениями, особенно интересен показатель риска, который называется коэффициентом вариации (Vr), который представляет собой отношение среднего квадратического отклонения к среднему ожидаемому значению и показывает степень отклонения полученных значений.
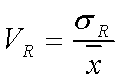(17)
По физическому смыслу коэффициент вариации отражает количество риска на единицу доходности, те есть по степени охвата деятельности он является комплексным.
Этот показатель является относительной величиной, поэтому на его размер не оказывают влияние абсолютные значения ожидаемого результата, и с его помощью можно даже сравнить колеблемость признаков, выраженных в разных единицах измерения.
Диапазон коэффициента вариации 0 – 100%. Чем выше показатель, тем сильнее колеблемость и риск предпринимательской деятельности.
Шкала оценки показателя коэффициента вариации выглядит следующим образом:
До 10% - слабая колеблемость;
10 – 25 % - умеренная колеблемость;
Свыше 25 % - высокая колеблемость.
Данный коэффициент используют также для определения однородности совокупность результатов предпринимательской деятельности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному).
Таким образом,
- с помощью статических показателей оценки риска можно оценить риск не только конкретной сделки, но и предпринимательской фирмы в целом на основе её доходов за некоторый промежуток времени;
- преимущество статистических показателей – несложность расчетов; недостаток – необходимость добывания большого объема исходных данных, что ограничивает применение этих показателей;
- дисперсия сигнализирует о наличии риска, но при этом не показывает направления отклонения от ожидаемого значения, так как в формуле в знаменателе стоит квадрат разности. Предпринимателю же важно знать знак этого отклонения, который означает прибыли или убытки.
- особенностью статистических показателей риска является то, что по ним не всегда можно принять однозначное решение в пользу того или иного варианта, т. к. необходимо также учитывать доходность и др. и иметь четкое представление о критериях принятия решений.
2.4. Показатели риска в условиях полной неопределенности: экспертные показатели оценки риска и критерии выбора рисковых решений
2.4.1. Экспертные оценки как методы принятия рисковых решений
Условия полной неопределенности – ситуация, в которой известны возможные варианты развития событий, информация о вероятности наступления рисковых ситуаций полностью отсутствует, но существует возможность привлечения специалистов и экспертов для частичного снятия неопределенности.
Полная неопределенность часто встречаются в предпринимательской деятельности в условиях нестабильной среды, когда повторение экономических ситуаций практически невозможно и отсутствует информация о возможности появления рисковых событий. Поэтому можно использовать субъективные методы экспертных оценок, суждений и личного опыта экспертов и специалистов в области финансового менеджмента.
Методы экспертной оценки представляют собой комплекс логических и математических процедур, направленных на получение от специалистов-экспертов информации, её анализ и обобщение с целью выбора рациональных решений.
Опрос экспертов осуществляется в соответствии с выбранным методом экспертных оценок. Существует большое количество методов сбора и обработки информации, полученной с помощью экспертов. Коллективное мнение экспертов может быть выражено в формах:
- количественных оценок в единицах измерения или в виде соотношения хуже-лучше);
- балльных оценок;
- попарных сравнений;
- группировок (сортировки);
- ранжирования и шкалирования и др.
Средством сбора информации от экспертов является, чаще всего, опросный лист-анкета, которая должна удовлетворять требованиям простоты, однозначности понимания текста, краткости и полноты изложения, иллюстративности, однотипности.
При организации процедуры экспертизы важным является вопрос об установлении количества экспертов, так как при малом их количестве проявляется излишнее влияние оценки каждого эксперта, а при большом - трудно вырабатывается единое мнение. Существует зависимость между достоверностью экспертизы и количеством экспертов. Как правило, в составе группы экспертов рекомендуется иметь не менее 5-12 специалистов.
Среди методов экспертных оценок как научного инструмента трудноформализуемых задач анализа предпринимательского риска наиболее примелем метод Дельфи, или метод дельфийского оракула.
Он представляет собой процедуру итеративного многоуровневого опроса. Является одним из основных при проведении экспертиз и имеет различные модификации. Фактически в настоящее время представляет группу методов, объединенных общими требованиями к организации и форме получения экспертных оценок.
Свое название этот способ получил по храму греческого города Дельфы, где находился знаменитый во всем античном мире оракул, предсказывающий будущее. Предполагается, что предсказания оракула коллективно готовились жрецами храма, используя данную методику.
Требованиями к организации данной процедуры выступают анонимность экспертов, возможность пополнить информацию о предмете экспертизы, обеспечение экспертов информацией по результатам оценок после каждого тура с сохранением анонимности.
Сущность метода Дельфы состоит в том, что каждый результат (прогноз на будущее) разрабатывается в несколько туров, и на каждом этапе используются результаты предыдущего тура опроса экспертов.
На первом туре экспертам предлагается информация о целях, объекте и предмете экспертизы, дается необходимая информация об объекте, и предлагается ряд вопросов (вариантов), на которые необходимо дать ответ (оценить). Эксперты делают оценки и ранжируют те варианты, которые им представили организаторы опроса или которые они сами наметили в качестве ответа на вопросы. Обработка информации перового тура сводится к определению медианы (середины упорядоченного ряда) и квартилей (середин отрезков, образовавшихся слева и справа от медианы). Результатом, соответственно, становиться усредненная оценка и наиболее радикальные варианты, предложенные экспертами. Тех экспертов, чьи оценки выходят за диапазоны верхнего и нижнего квартилей (границ), просят обосновать свои суждения и сообщить свое мнение по поводу совершенства постановки вопроса. Их аргументы могут включать учет каких-то дополнительных факторов, которые не учитывались другими специалистами.
Схематично результаты опроса можно представить следующим образом:
О1……..К1……..М……..К2……..Оm, где
О1…Оm – полученные оценки, расположенные в порядке их убывания;
М – медиана – значение оценки, выпавшее на середину упорядоченного ряда;
К1, К2 – квартили – значения середин отрезков, расположенных слева и справа от медианы.
На втором туре экспертам направляются полученные результаты и радикальные обоснования первого тура (без указания, от кого они получены), их просят проанализировать данные и снова ответить на те же самые вопросы. Эксперты уточняют ответы, пользуясь, в случае необходимости, дополнительной информацией. Процедура обработки ответов и формулирования информации о результатах повторяется.
Организация третьего тура происходит тем же образом. На нем эксперты получают не только результаты упорядочения данных, но и статистическое описание мнений всех членов группы и сводку аргументов сторонников верхней и нижней оценок. Подобная процедура позволяет экспертам учесть большее число факторов и в случае необходимости скорректировать свое мнение.
В следующих турах все повторяется в той же последовательности. Медиана оценок последнего тура принимается за обобщенное мнение. Результаты последующих туров опроса дают, как правило, все меньший и меньший разброс оценок. Считается, что при такой организации процедуры достаточно 4 туров для нахождения более или менее однозначного решения.
Таким образом, метод Дельфы - экспертный метод комплексного анализа альтернативных управленческих решений, основанный на их генерации в процессе "мозговой атаки", проводимой группой высококвалифицированных в этой области специалистов, отборе наиболее рационального для данной ситуации решения.
2.4.2. Правила и критерии принятия решений в условиях полной неопределённости
Принятие решений в условиях неопределенности зависит от сопоставления полезности различных исходов, и направлено на выбор такого решения, которое приносит наибольшую ожидаемую полезность. При принятии решений в условиях полной неопределенности в ситуациях, когда невозможно сделать однозначный выбор из нескольких вариантов, можно руководствоваться не только личным опытом, но и специальными правилами (критериями). Данные критерии применяются в условиях, когда нет ни объективных, ни субъективных вероятностей исходов. Они получили название классических и применимы для большей части управленческих решений в кризисных ситуациях.
Задача выбора решения в условиях неопределённости сводится к следующему.
Пусть задан некоторый вектор S = (S1,S2,..,Sn), описывающий n состояний внешней среды, и вектор X = (X1,X2,..,Xm), описывающий m допустимых решений. Требуется найти такой вектор X* =(0,0,..,0, Xi,0,..,0), который бы обеспечивал оптимум некоторой функции полезности W(X, S) по некоторому критерию K.
Значение оптимума функции W(X, S) раскрывается, исходя из постановки конкретной задачи (к примеру, если обсуждается получение прибыли, то значение функции стремятся максимизировать, если себестоимость – минимизировать).
Информацию об указанной функции полезности (по сути - исходные данные задачи такого типа) представляют матрицей c элементами Wij = F(Xi, Sj), где F - решающее правило (определяемое из постановки конкретной задачи). При достаточно четкой экономической постановке задачи практически не возникает проблем с формированием матрицы {Wij}.
Существует несколько общих критериев рационального выбора вариантов решений из множества возможных. Критерии основаны на анализе матрицы возможных состояний окружающей среды и альтернатив решений.
Матрица, приведенная в таблице 7, содержит:
Аj - альтернативы, т. е. варианты действий, один из которых необходимо выбрать (управляемые факторы);
Si - возможные варианты состояний окружающей среды (неуправляемые факторы);
aij - элемент матрицы, обозначающий значение стоимости капитала, принимаемое альтернативой j при coстоянии окружающей среды i.
Таблица 7
Матрица решений
Альтернатива
Si (состояние среды)
S1
S2
…
Si
…
Sm
А1
а11
а12
…
а1i
…
а1m
Аj
аj1
аj2
…
аji
…
аjm
Аn
аn1
аn2
…
аni
…
аnm
Для выбора оптимальной стратегии в ситуации неопределённости используются следующие правила и критерии.
1. Критерий Лапласа
По принципу недостаточного основания в условиях, когда невозможно выяснить вероятности для возникновения того или иного состояния внешней среды, им сопоставляют равные вероятности, находят средний эффект для каждого из рассматриваемых вариантов решения и выбирается тот из них, где средний эффект максимален:
W =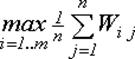 
(18)
2. Критерий Вальда (критерий наибольшей осторожности/ пессимиста; правило максимин).
Для каждого из рассматриваемых вариантов решения Xi выбирается самая худшая ситуация (наименьшее из Wij) и среди них отыскивается гарантированный максимальный эффект:
W = 
(19)
Принимающий решение в этом случае готов к риску, предполагая максимум негативного развития состояния внешней среды (самое худшее, минимальное значение) и учитывая свою возможность действовать в этой ситуации наиболее оптимально (выбор наилучшей, максимальной альтернативы).
3. Критерий Гурвица
Используя этот критерий, исходят из того, что ориентация на самый худший исход является своеобразной перестраховкой, однако опрометчиво выбирать и излишне оптимистичную политику. При выборе решения необходимо идти на некоторый компромисс.
Это правило называют ещё правилом оптимизма – пессимизма. Оптимальную альтернативу можно рассчитать по формуле:
W = 
(20)
где α - коэффициент оптимизма, α = 1…0.
При α =1 альтернатива выбирается по правилу максимакс (т. е. берется наилучший возможный вариант), при α = 0 этот критерий превращается в критерий Вальда (полный пессимизм), при α = 0,5 мы расцениваем равновероятно шансы на успех и неудачу, при α = 0,2 мы более осторожны и вероятность успеха считаем меньшей (0,2) чем возможную неудачу.
Учитывая боязнь риска, целесообразно задавать α =0,3. Наибольшее значение целевой величины и определяет необходимую альтернативу.
Правило Гурвица применяют, учитывая более существенную информацию, чем при использовании правил максимин и максимакс.
4. Правило минимального риска (критерий Сэвиджа)
В отличие от максимина этот критерий ориентирован на минимизацию не столько потерь, сколько сожалений по поводу упущенной прибыли. Правило допускает разумный риск ради получения дополнительной прибыли. Суть его - нахождение минимального риска.
Критерий Сэвиджа определяется путем построения матрицы сожалений (матрица Сэвиджа) и рассчитывается следующим образом:
1. Находится лучший результат каждой графы в отдельности, то есть максимум 
(реакции рынка).
2. Определяется отклонение от лучшего результата каждой отдельной графы, которое будет составлять элементы матрицы сожалений:
Dij = Wij - max (Wij) (21)
Полученные результаты образуют матрицу отклонений (сожалений), так как её элементы – это недополученная прибыль от неудачно принятых решений, допущенных из-за ошибочной оценки возможности реакции рынка.
3. По матрице D выбирается решение по пессимистическому критерию Вальда, дающее наименьшее значение максимального сожаления
W =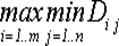 
(22)
То есть, выбираем решение, при котором максимальное сожаление будет меньше других.
Вполне логично, что различные критерии приводят к различным выводам относительно наилучшего решения. Вместе с тем возможность выбора критерия дает свободу лицам, принимающим экономические решения (если они, конечно, располагают достаточными средствами для постановки подобной задачи). Любой критерий должен согласовываться с намерениями решающего задачу и соответствовать его характеру, знаниям и убеждениям.
Выводы:
1. Показатель риска является мерой проявления рискового события и характеризует несоответствие результатов деятельности нормативным требованиям, возможные потери ресурсов или возможные отклонения фактической прибыли от ожидаемой.
2. В зависимости от полноты информации, имеющейся у субъекта управления, показатели оценки риска разбиваются на показатели в условиях определенности, в условиях частичной неопределенности (риска) и полной неопределенности.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 |
