Задачи обучающего тура
Уровень 2
(Для команд, основной состав которых учащиеся 8-11 классов)
Задача №1
Остап Бендер и Киса Воробьянинов разделили между собой выручку от продажи слонов населению. Остап подумал: если бы я взял денег на 40% больше, то доля Кисы уменьшилась бы на 60%. А как изменилась бы доля Воробьянинова, если бы Остап взял себе денег на 50% больше?
Решение
Пусть Остап взял себе x рублей, а Киса взял себе y рублей, тогда, по условию, 0,4x = 0,6y. Отсюда получим, что 0,5x = 0,75y. Следовательно, если бы доля Остапа увеличилась на 50%, то доля Воробьянинова уменьшилась бы на 75%.
Ответ: доля Воробьянинова уменьшилась бы на 75%.
Задача №2
Под какой процент выгоднее положить деньги в банк на год: 6 процентов в год или 1/2 процентов в месяц?
Подсказка
Если бы 1/2 процента каждый месяц начислялись от суммы, положенной в банк в начале года, то в конце года сумма увеличилась бы на 6 процентов.
Решение
Пусть в банке начисляется 1/2 процентов каждый месяц. Если бы 1/2 процента каждый месяц начислялись от суммы, положенной в банк в начале года, то в конце года (через 12 месяцев) сумма увеличилась бы как раз на (1/2)*12=6 процентов. Однако, начиная со второго месяца 1/2 процента будет начисляться от суммы, которая находится в банке к началу месяца, т. е. от суммы, которая больше, чем положенная в начале года. Поэтому в конце года сумма окажется больше в том случае, если каждый месяц начисляется по 1/2 процента.
Ответ: выгоднее второй вариант
Задача №3
Экологи запротестовали против большого объема лесозаготовки. Председатель леспромхоза успокоил их следующим образом: "В лесу 99 процентов сосен. Будут вырубаться только сосны, и после вырубок процент сосен останется почти неизменным - сосен будет 98 процентов". Какая часть леса отведена под вырубки?
Подсказка
Количество "не сосен" остается постоянным, а доля "не сосен" увеличилась с одного процента до двух...
Решение
Обозначим через x число деревьев, не являющихся соснами. Тогда до вырубки x составляет 100-99=1 процент леса, а после вырубки x составляет 100-98=2 процента леса. Таким образом, до вырубки в лесу было 100x деревьев, а после вырубки должно остаться 50x деревьев, т. е. в два раза меньше.
Ответ. половина.
Задача №4
По данным опроса, проведенного в 8 "Е" классе, выяснилось, что 20 % учеников, интересующихся математикой, интересуются еще и физикой, а 25 % учеников, интересующихся физикой, интересуются также и математикой. И только Пете с Васей не интересен ни один из этих предметов. Сколько человек в 8 "Е", если известно, что их больше 20 , но меньше 30?
Решение
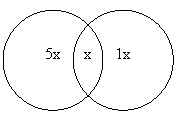
Количество человек в 8 "Е" без учета Пети и Васи превышает 18, но меньше, чем 28. Пусть x учеников класса интересуются одновременно и математикой, и физикой. Тогда всего математикой интересуются 5x учеников, а физикой– 4x учеников. Значит, математикой или физикой интересуются 5x + 4x - x = 8x учеников. Таким образом, количество учеников в классе должно делиться на 8. В указанных границах есть только одно число, кратное восьми. Следовательно, 8x = 24 , а всего в классе– 26 человек.
Ответ. 26
Задача №5
В семье 4 человека. Если Маше удвоят стипендию, общий доход всей семьи возрастет на 5%, если вместо этого маме удвоят зарплату – на 15%, если же зарплату удвоят папе – на 25%. На сколько процентов возрастет доход всей семьи, если дедушке удвоят пенсию?
Решение
Решение. Если Маше удвоят стипендию, семейный доход возрастёт на размер этой стипендии. Следовательно, Машина стипендия составляет 5% общего дохода. Аналогично, мамина зарплата составляет 15%, а папина – 25%. Оставшаяся доля 100%-5%-15%-25%=55% приходится на дедушкину пенсию. Значит, если ему удвоят пенсию, доход всей семьи возрастёт на 55%.
Это же решение можно сформулировать по-другому. Если бы всем членам семьи вдруг стали платить вдвое больше, общий доход увеличился бы на 100%. Из этих 100 процентов 5 приходится на Машу, 15 – на маму, 25 – на папу, а остальные 55 – на дедушку.
Ответ. на 55%
Задача №6
Мама дала Васе денег на 30 карандашей. Оказалось, что в магазине карандашная фабрика проводит рекламную акцию: в обмен на чек о покупке набора из 20 карандашей возвращают 25% стоимости набора, а в обмен на чек о покупке набора из 5 карандашей 10%. Какое наибольшее число карандашей может купить Вася?
Решение
Заметим, что 25% от стоимости 20 карандашей - это стоимость 5 карандашей, а 10% от стоимости 5 карандашей - это половина стоимости карандаша.
Ясно, что для получения максимальной скидки Вася должен действовать так:
1. Пока хватает денег, покупать набор из 20 карандашей и сразу обменивать чек на выходе;
2. если не хватает денег на 20 карандашей, но хватает на 5, покупать набор из 5 карандашей и сразу обменивать чеки на выходе;
3. в крайнем случае покупать отдельные карандаши.
Действуя таким образом, Вася сначала купит коробку из 20 карандашей и получит на выходе из магазина стоимость 5 карандашей. После этого у него будет денег на 15 карандашей. Потом он купит три набора из 5 карандашей и получит на выходе стоимость 1, 5 карандашей. На оставшиеся деньги он купит 1 карандаш. Итого: 36 карандашей.
Ответ. 36 карандашей.
Задача №7
Груз весом 13, 5 т упакован в ящики так, что вес каждого ящика не превосходит 350 кг. Докажите, что этот груз можно перевезти на 11 полуторатонках. (Весом пустого ящика можно пренебречь.)
Решение
Выделим 8 машин и будем последовательно их грузить, причём каждый раз тот ящик, который уже нельзя погрузить, будем ставить рядом с машиной. Погруженные ящики вместе с ящиками, стоящими рядом с машинами, весят более 8 . 1, 5 = 12 т, поэтому оставшиеся ящики весят менее 1, 5 т; их можно увезти на одной полуторатонке. Поскольку 4 . 350 = 1400 < 1500, на одной машине можно увезти любые 4 ящика. Значит, 8 ящиков, стоящих рядом с машинами, можно увезти на двух оставшихся полуторатонках.
Ответ. груз можно перевезти на 11 полуторатонках
Задача №8
Наташа и Инна купили по одинаковой коробке чая в пакетиках. Известно, что одного пакетика хватает на две или три чашки чая. Этой коробки Наташе хватило на 41 чашку чая, а Инне — на 58. Сколько пакетиков было в коробке?
Решение
Заметим, что в коробке не могло быть меньше 20 пакетиков: если их хотя бы 19, то Инна не сможет выпить больше 19 . 3 = 57 чашек, а она выпила 58. С другой стороны, в коробке
не могло быть больше 20 пакетиков: если их хотя бы 21, то Наташа не могла выпить меньше 21 . 2 = 42 чашек, а она выпила 41. Тем самым, в коробке было 20 пакетиков: Инна заварила 18 пакетиков по три раза и 2 пакетика по два раза, а Наташа заварила 1 пакетик три раза и 19 пакетиков по два раза.
Замечание. Обязательно надо предъявить способ выпить 41 и 58 чашек чая, иначе решение будет не полным.
Ответ. 20 пакетиков.
Задача №9
У капитана Смоллетта двое сыновей и несколько дочерей. Если возраст капитана (конечно, ему меньше ста лет) умножить на количество его детей и на длину его шхуны (это целое число футов), то получится 32118. Сколько лет капитану Смоллетту, сколько у него детей и какова длина его корабля?
Подсказка
Разложите 32118 на множители.
Решение
Пусть x - число детей, которых больше трех, т. к. у капитана есть два сына и несколько дочерей; y - возраст капитана; z - длина корабля в футах. Из условия задачи следует, что xyz=32118 и 3<x, y<100. Число 32118 раскладывается в произведение простых множителей как 2 ∙ 3 ∙ 53 ∙ 101. Есть шесть способов представления этого числа в виде трех множителей: 6 ∙ 53 ∙ 101; 3 ∙ 101 ∙ 106; 3 ∙ 53 ∙ 202; 2 ∙ 101 ∙ 159; 2 ∙ 53 ∙ 303; 2 ∙ 3 ∙ 5353. Только первое из этих разложений содержит два множителя между 3 и 100. Следовательно, у капитана 6 детей; ему 53 года; и длина его корабля равна 101 футу.
Ответ. 6 детей; ему 53 года; и длина его корабля равна 101 футу.
Задача №10
Петя играет в игру-стрелялку. Если он наберет менее 1000 очков, то компьютер добавит ему 20 % от его результата. Если он наберет от 1000 до 2000 очков, то компьютер добавит ему 20 % от первой тысячи очков и 30 % от оставшегося количества очков. Если Петя наберет более 2000 очков, то компьютер добавит ему 20 % от первой тысячи очков, 30 % от второй тысячи и 50 % от оставшегося количества. Сколько призовых очков получил Петя, если по окончании игры у него было 2370 очков?
Решение
Если бы Петя набрал менее 1000 очков, то его результат был бы меньше, чем 1200 очков. Если бы Петя набрал 2000 или более очков, то количество призовых очков составило бы не менее, чем 0,2· 1000 + 0,3· 1000 = 500 . Вэтом случае его результат– не менее 2500 очков. Следовательно, Петя набрал 1000 + х очков, где х (0;1000) . Компьютер добавил ему 200 очков за первую тясячу и 0,3х очков– за остальное. Таким образом, 1000 + х + 200 + 0,3х = 2370 ![]() х = 900 . Тогда количество призовых очков равно 470.
х = 900 . Тогда количество призовых очков равно 470.
Ответ. 470.
Задача №11
В одном стакане было молоко, а в другом - столько же кофе. Из стакана молока перелили одну ложку в стакан с кофе и размешали. Затем такую же ложку смеси перелили обратно в стакан с молоком. Чего теперь больше: кофе в стакане с молоком или молока в стакане с кофе?

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 |



