Задачи обучающего тура (стр. 5 )

Решение

Пусть процентное содержание хрома в первом и втором сортах стали р% и q% соответственно.

Если ваять 5m кг стали первого сорта и т кг стали второго сорта, то процентное содержание хрома в сплаве составит

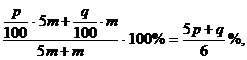
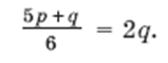что по условию задачи равно 2q% . Составим первое уравнение: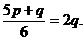

Если взять по n кг стали первого и второго сорта, то процентное содержание хрома в сплаве составит

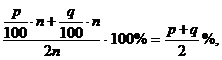
что по условию задачи равно 8%. Составим второе уравнение:

Упростив эти уравнения и решив систему

получим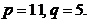

Итак, процентное содержание хрома в первом и во втором сплавах составляет 11% и 5%.

Ответ. Процентное содержание хрома в первом и во втором сплавах составляет 11% и 5%.

Задача №29

В двух одинаковых сосудах, объемом по 30 л каждый, содержится всего 30 л спирта. Первый сосуд доливают доверху водой и полученной смесью дополняют второй сосуд, затем из второго сосуда отливают в первый 12 л новой смеси. Сколько литров спирта было первоначально в первом сосуде, если во втором сосуде оказалось на 2 л спирта меньше, чем в первом?

Решение

Сначала заметим, что в конце всех переливаний в первом сосуде оказалось 16 л, а во втором – 14 л спирта. Пусть в первом сосуде первоначально было х л спирта, тогда во втором было (30 – х) л спирта. Когда в первый сосуд долили воду, то спирт в нем составлял всего объема.

Из первого сосуда во второй перелили х л смеси, содержащей спирта, и во втором сосуде стало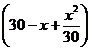 л спирт.

Доля спирта во втором сосуде стала равной дроби 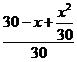поэтому в 12 л смеси, перелитой в первый сосуд, содержалось чистого спирта

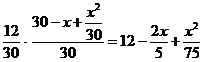
Итак, во втором сосуде осталось

спирта или 14 л. Составим уравнение:

.

Уравнение имеет два корня х = 10 и х = 20, при этом нет оснований для исключения одного из корней.

Проверим, действительно ли эти задача имеет два решения,

1) Если в первом сосуде было 10 л, тогда во втором было 30 – 10 = 20 л спирта. В первый сосуд долили 20 л воды, в полученной смеси доля спирта составила, поэтому во второй сосуд перелили л спирта. Во втором сосуде стало , и доля спирта составила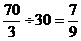 поэтому в первый сосуд перелили л спирта, а во втором сосуде осталось 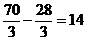л спирта.

2) Если в первом сосуде было 20 л, тогда во втором было 30 - 20 = 10 л спирта. В первый сосуд долили 10 л воды, в полученной смеси доля спирта составила , поэтому во второй сосуд перелили л спирта. Во втором сосуде стало 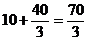л. Результат повторился, поэтому дальнейшие вычисления приведут к тому же ответу.

Итак, проверка показала, что задача имеет два решения.

Ответ. 10 л. или 20 л.

Задача №30

Имеется два бака: первый наполнен глицерином, а второй водой. Взяли два двухлитровых ковша, зачерпнули первым ковшом доверху глицерин из первого бака, вторым ковшом — воду из второго бака, после чего первый ковш влили во второй бак, а второй ковш — в первый бак. После перемешивания повторили эту операцию со смесями еще раз. В результате 40% объема первого бака занял чистый глицерин. Определить суммарный объем баков, если по объему второй бак в 4 раза больше первого.

Решение

Пусть V — объем первого бака (V > 2), тогда 4V — объем второго бака. В авторском решении предлагается проследить изменение объемов воды и глицерина в каждом баке. Сократим вычислительную работу, отслеживая изменение содержания глицерина только в первом баке.

Объем глицерина, оставшегося в первом баке после первого переливания, равен , доля глицерина в первом баке составляла , а во втором баке — , поэтому объем глицерина, взятого во второй раз из первого бака, равен 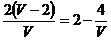, а влитого во второй бак .

Объем глицерина, оказавшегося после двух переливаний в первом баке, равен , или 0,4V. Составим уравнение:

.

Это уравнение имеет два корня и V = 5, но первый из них не удовлетворяет условию V > 2, поэтому V = 5, тогда V + 4V = 25.

Ответ. 25

Задача №31

На факультете X отличники составляют 10% от общего количества студентов этого факультета, на факультете Y — 20%, а на факультете Z — лишь 4%. Найти средний процент отличников по всем трем факультетам, если известно, что на факультете Y учится на 50% больше студентов, чем на факультете X, а на факультете Z вдвое меньше, чем на факультете X.

Решение

Поскольку требуется найти отношение, то можно смело вводить «лишнее» неизвестное.

Пусть на факультете X учится х студентов, тогда на всех трех факультетах учится х + 1,5х + 0,5х = Зх студентов, отличников среди них 0,1 ∙ х + 0,2 ∙ 1,5х + 0,04 ∙ 0,5х = 0,42х.

Они составляют .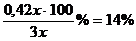

Ответ. 14%

Задача №32

Три мотоциклиста А, В и С участвовали в показательном заезде, двигаясь по трассе от старта до финиша с постоянными скоростями. Мотоциклисты А и С стартовали одновременно, а мотоциклист В спустя некоторое время. Первым к финишу пришел мотоциклист А. Мотоциклист В через 1 ч после своего старта догнал мотоциклиста С на трассе и прибыл на финиш через 4 ч после старта мотоциклистов А и С и за 2 ч до финиша мотоциклиста С. Найти отношение скорости мотоциклиста А к скорости мотоциклиста С, если известно, что мотоциклист А двигался в раза медленнее мотоциклиста В.

Решение:

Изобразим графики движения мотоциклистов А, В и С (рис. 1). Пусть мотоциклист В стартовал через х ч после мотоциклистов А и В.

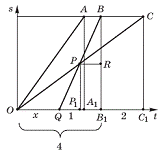
(рис. 1)

Так как все три мотоциклиста проехали один и тот же путь, то отношение их скоростей обратно пропорциональны промежуткам времени, потраченным на этот путь.

Так как отношение скоростей В и А равно , то , а требуется найти отношение скоростей А и С, равное .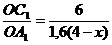

Тогда из подобия треугольников OQP и СВР следует, что

.

А из подобия треугольников QРP1 и РВR следует, что .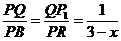

Составим уравнение .

Это уравнение имеет два корня 1 и 2.

При х = 1 промежуток времени ОА1 = 1,6(4 – 1) = 4,8 ч – это больше промежутка времени ОВ1 = 4 ч, что противоречит условиям задачи. Следовательно, условию задачи удовлетворяет только х = 2. В этом случае ОА1 = 1,6(4 – 2) = 3,2 ч

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7