Задачи обучающего тура (стр. 4 )

Ответ: гангстер должен двигаться навстречу полицейским со скоростью 2v или v/2 .

Задача №23

Несколько школьников ходили за грибами. Школьник, набравший наибольшее количество грибов, собрал общего количества грибов, а школьник, набравший наименьшее количество грибов, собрал часть от общего количества. Сколько было школьников?

Решение

Первый способ. Пусть было собрано x грибов и было n школьников. Тогда каждый школьник собрал не менее, чем и не более, чем грибов. Значит, все школьники собрали не менее, чем 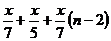грибов, но не более, чем грибов. Таким образом, выполняется неравенство: 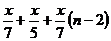≤ x≤ . Упростив его, получим: ≤1≤ , то есть, . Учитывая, что n – целое, получим, что n=6 .

Второй способ. Так как количество грибов– целое, то оно должно делиться на 5 и на 7, то есть, должно делиться на 35. Пусть было 35 k грибов ( k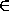 N ). Тогда первый собрал 7k грибов, последний– 5k грибов, а остальные школьники собрали 23 k грибов. Каждый из оставшихся школьников собрал не меньше, чем 5k грибов, но не больше, чем 7k грибов. Следовательно, оставшихся грибников больше, чем , но меньше, чем . Таким образом, их четверо, а всего было шесть школьников.
Отметим, что рассматриваемый случай возможен, например, если школьники собрали 5k, 5k , 6k , 6k , 6k и 7k грибов соответственно.

Ответ. шесть.

Задача №24

Али-Баба пришел в пещеру, где есть золото, алмазы и сундук, в котором их можно унести. Полный сундук золота весит 200 кг, полный сундук алмазов — 40 кг, пустой сундук ничего не весит. Килограмм золота стоит на базаре 20 динаров, килограмм алмазов — 60 динаров. Али-Баба может поднять и унести не более 100 кг. Сколько денег он может получить за сокровища, которые он принесет из пещеры за один раз?

Решение

Предположим, что Али-Баба смог унести из пещеры x кг золота и y кг алмазов. В этом случае он сможет получить 20x + 60y динаров. Поскольку Али-Баба может поднять не более 100 кг, то

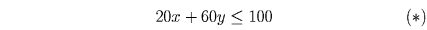
Кроме того, 1 кг золота занимает часть сундука, а 1 кг алмазов занимает часть сундука. Значит, взятые Али-Бабой сокровища займут часть сундука. В распоряжении Али-Бабы только один сундук, поэтому получаем новое ограничение на количество взятого им сокровища:

или, умножив последнее неравенство на 200,

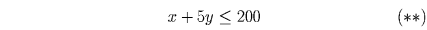
Сложим неравенства (*) и (**): 2x + 6y ≤ 300 Умножим обе части последнего неравенства на 10: 20x + 60y ≤ 3000 Значит, Али-Баба сможет получить за сокровища не более 3000 динаров.

Осталось показать, что Али-Баба сможет унести сокровища на 3000 динаров. Для этого, очевидно, необходимо и достаточно чтобы в неравенствах (*) и (**) были выполнены равенства. Решив соответствующую систему двух уравнений, найдем x = 75, y = 25.

Итак, Али-Баба сможет получить 3000 динаров, взяв из пещеры 75 кг золота и 25 кг алмазов.

Ответ. 3000 динаров

Задача №25

В магазине три этажа, перемещаться между которыми можно только на лифте. Исследование посещаемости этажей магазина показало, что с начала рабочего дня и до закрытия магазина:

1)  из покупателей, входящих в лифт на втором этаже, половина едет на первый этаж, а половина - на третий;

2)  среди покупателей, выходящих из лифта, меньше трети делает это на третьем этаже.
На какой этаж покупатели чаще ездили с первого этажа, на второй или на третий?

Решение

Первое решение. Предположим, что за весь день на первом этаже в лифт вошло x покупателей, на втором - y, на третьем - z. Заметим, что количество покупателей, вышедших из лифта на каждом из этажей, равно количеству покупателей, вошедших на этом же этаже.

По условию, из покупателей, вошедших на втором этаже, половина едет вниз, а половина - вверх. Значит, со второго этажа на третий едет y/2 покупателей, и столько же со второго на первый. Второе условие можно записать так: z<(x+y+z)/3. Это равносильно тому, что 2z<x+y.

С первого этажа на третий было совершено z-(y/2) поездок, так как всего на третьем этаже вышли из лифта z человек, а y/2 из них приехали со второго этажа. А с первого на второй поднимались те покупатели, входившие в лифт на первом этаже, кто не ехал на третий, т. е. x-(z-(y/2)). Для решения задачи требуется сравнить эти два выражения. Но неравенство z-(y/2)<x-(z-(y/2)) равносильно уже доказанному неравенству 2z<x+y. Тем самым мы доказали, что с первого этажа на третий за этот день приехало меньше покупателей, чем с первого на второй.

Второе решение. Обозначим через n12 количество поездок с первого этажа на второй. Аналогично определим числа n13, n21, n23, n31, n32. Все поездки разобьём на три группы: поездки на третий этаж, поездки с третьего этажа и поездки между первым и вторым этажом. По условию задачи, первая группа составляет менее трети всех поездок. С другой стороны, она количественно равна второй, так как число покупателей, приехавших на третий этаж равно числу уехавших с третьего этажа. Значит, последняя группа составляет более трети всех поездок:

(n31+n32)=(n13+n23)<(n12+n21).

Подставляя в это неравенство n21=n23, получим n13<n12: с первого этажа чаще ездили на второй, нежели на третий.

Ответ: с первого на третий этаж за этот день приехало меньше покупателей, чем с первого на второй.

Задача №26

Дети держат в руках флажки. Тех, у кого в обеих руках поровну флажков, в 5 раз меньше, чем тех, у кого не поровну. Когда каждый ребёнок переложил по одному флажку из одной руки в другую, тех, у кого в обеих руках поровну флажков, стало в 2 раза меньше, чем тех, у кого не поровну. Могло ли быть так, что в начале более чем у половины детей в одной руке было ровно на один флажок меньше, чем в другой?

Подсказка

Обратите внимание: если у ребёнка было поровну флажков в обеих руках, то после перекладывания у этого ребёнка флажков станет не поровну.

Решение

В начале было n/6 детей, у которых в руках было поровну флажков, и 5n/6 детей, у которых не поровну. Допустим, что в начале у n/2 + a детей в одной руке было ровно на один флажок меньше, чем на другой. Тогда после перекладывания у этих n/2 + a детей будет неравное количество флажков в руках, да и у тех n/6 детей, у которых в начале было поровну, тоже будет не поровну. Значит, всего не поровну будет (n/2 + a) + n/6 > 2/3. Мы пришли к противоречию, которое доказывает, что в начале менее чем у половины детей в одной руке было ровно на один флажок меньше, чем в другой.

Ответ.  Нет.

Задача №27

Один сплав состоит из двух металлов, входящих в него в отношении 1 : 2, а другой содержит те же металлы в отношении 2 : 3. Из скольких частей обоих сплавов можно получить новый сплав, содержащий те же металлы в отношении 17 : 27?

Решение

Пусть взяли х кг первого и у кг второго сплава. Тогда в новом сплаве первого металла cодержится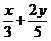 кг, а второго металла - кг.

Отношение этих масс равно 17 : 27. Составим уравнение:

Откуда .

Это означает, что на 9 частей первого металла нужно взять 35 частей второго.

Ответ. на 9 частей первого металла нужно взять 35 частей второго

Задача №28

Сплавили два сорта стали с разным процентным содержанием хрома. Если первого сорта взять в 5 раз больше второго, то процентное содержание хрома в сплаве вдвое превысит процентное содержание хрома в меньшей из сплавляемых частей. Если же взять одинаковое количество, то сплав будет содержать 8% хрома. Определите процентное содержание хрома в каждом сорте стали.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7