=5 Û (x + y + z) 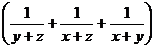=5.

Значит,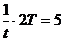, то есть T : t = 2, 5.

Ответ. В 2,5 раза.

Задача №17

Как-то Кролик торопился на встречу с осликом Иа-Иа, но к нему неожиданно пришли Винни-Пух и Пятачок. Будучи хорошо воспитанным, Кролик предложил гостям подкрепиться. Пух завязал салфеткой рот Пятачку и в одиночку съел 10 горшков меда и 22 банки сгущенного молока, причем горшок меда он съедал за 2 минуты, а банку молока – за минуту. Узнав, что больше ничего сладкого в доме нет, Пух попрощался и увел Пятачка. Кролик с огорчением подумал, что он бы не опоздал на встречу с осликом, если бы Пух поделился с Пятачком. Зная, что Пятачок съедает горшок меда за 5 минут, а банку молока – за 3 минуты, Кролик вычислил наименьшее время, за которое гости смогли бы уничтожить его запасы. Чему равно это время? (Банку молока и горшок меда можно делить на любые части).

Решение

Ясно, что Пух и Пятачок должны закончить есть одновременно, иначе один из них сможет помочь другому, уменьшив тем самым общее время, затраченное на еду. Пусть Пух съел x1 горшков меда и y1 банок сгущенного молока, а Пятачок – x2 горшков меда и y2 банок молока ( x1 , x2 , y1 и y2 – не обязательно целые числа). Тогда для времени T , которое затрачено каждым из них на еду, получаем

T=2x1+y1=5x2+3y2,


причем x2=10-x1 , а y2=22-y1 . Следовательно,

2x1+y1=50-5x1+66-3y1,


откуда

y1=, T=+29.


Заметим, что y1≤22 , поэтому 116-7x1≤88 , т. е. x1≥4 . Значит, наименьшее время T получается при x1=4 и равно 30 минутам. При этом Пух должен съесть 4 горшка меда и всю сгущенку, а Пятачок – 6 горшков меда.

Ответ. 30 минут

Задача №18

Три каменщика разной квалификации выложили кирпичную стену, причём первый каменщик работал 6 часов, второй – 4 часа, а третий – 7 часов. Если бы первый каменщик работал 4 часа, второй – 2 часа и третий – 5 часов, то было бы выполнено 2/3 всей работы. За сколько часов каменщики закончили бы кладку, если бы они работали вместе одно и то же время?

Решение.

Решим эту задачу путём составления системы уравнений.

Пусть х – скорость выполнения работы первого каменщика, y – второго, z – третьего. Всю работу примем за 1. Составим систему уравнений по условию задачи (рис. 2а)

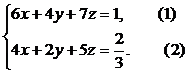
Надо найти , то есть

Умножим (2) на -2 и сложим почленно с (1). Получим:

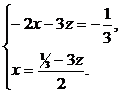
Затем умножим (2) на -1,5 и сложим почленно с (1). Получим:

y=0,5z

Следовательно, подставим в искомое выражение полученные значения для x, y. В итоге получим 6.

Ответ: каменщики выполнят эту работу за 6 часов.

Задача №19

Дима живет в девятиэтажном доме. Он спускается на лифте со своего этажа на первый за 1 минуту. Из-за маленького роста Дима не достает до кнопки своего этажа. Поэтому, поднимаясь наверх, он нажимает ту кнопку, до которой может дотянуться, а дальше идет пешком. Весь путь наверх занимает 1 минуту 10 секунд. Лифт движется вверх и вниз с одинаковой скоростью, а Дима поднимается вдвое медленнее лифта. На каком этаже живет Дима?

Решение

Первое решение. Рассмотрим ту часть пути, которую Дима вниз едет на лифте, а вверх идет пешком. С одной стороны путь пешком занимает вдвое больше времени, а с другой – больше на 10 секунд. Значит, эту часть пути он проехал за 10 секунд, а прошел пешком за 20 секунд. Поскольку весь путь на лифте занимает 60 секунд, то пешком он шел 1/6 пути. Заметим, что пешком он шел целое число промежутков между этажами. Поскольку дом девятиэтажный, пешком он шел 1 промежуток, а ехал 5. Значит, Дима живет на седьмом этаже. Второе решение. Пусть лифт движется со скоростью v этажей в секунду, Дима живет на n -м этаже, а выходит обычно на m -м. Тогда

откуда m-1+2n-2m=70v . Подставим v= из первого уравнения: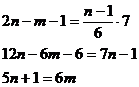

Так как m<9 , нетрудно найти, что n=7 , а m=6 .

Ответ. Дима живет на седьмом этаже.

Задача №20

Из пункта A в другие можно попасть двумя способами:

1. Выйти сразу и идти пешком.

2. Вызвав машину и, подождав ее определённое время, ехать на ней.

В каждом случае используется способ передвижения, требующий меньшего времени. При этом оказывается, что

если конечный пункт отстоит на

то понадобится на дорогу

1 км

10 мин

2 км

15 мин

3 км

17$ {\frac{1}{2}}$ мин

Скорости пешехода и машины, а также время ожидания машины, принимаются неизменными. Сколько понадобится времени для достижения пункта, отстоящего от A на 6 км?

Решение

Пусть v — скорость пешехода, V — скорость машины, T — время ожидания машины. (Скорость будем измерять в км/час, а время — в часах.) Если идти пешком, то на дорогу в 1, 2 и 3 км понадобится, соответственно, 1/v, 2/v и 3/v часов, а если ехать на машине, то T + , T + и T + часов. Предположим, что 2 км не медленнее пройти пешком, чем ехать на машине, т. е. T +. Тогда , т. е. 1 км тем более можно идти пешком. Но если можно идти пешком 1 км и 2 км, то тогда затраченное на 2 км время было бы ровно в 2 раза больше, чем на 1 км, а по условию это не так. Поэтому, а значит, 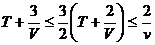. Следовательно, 1/v = 1/6, T + 2/V = 1/4 и T + 3/V = 7/24. Решая эту систему уравнений, находим: v = 6, T = 1/6, V = 24. Если идти 6 км пешком, то на это понадобится 1 час, а если ехать на машине, то понадобится , т. е. 25 мин.

Ответ. Если идти 6 км пешком, то на это понадобится 1 час, а если ехать на машине, то 25 мин.

Задача №21

В центре квадратного бассейна находится мальчик, а в вершине на берегу стоит учительница. Максимальная скорость мальчика в воде в три раза меньше максимальной скорости учительницы на суше. Учительница плавать не умеет, а на берегу мальчик бегает быстрее учительницы.

Сможет ли мальчик убежать?

Решение

Пусть учительница находится в вершине T (рис. 1). Сначала мальчик должен плыть к противоположной вершине V. Предположим, что учительница побежит по направлению к вершине W. Пусть в тот момент, когда учительница прибежит в W, мальчик доплывёт до точки C. Пусть TW = 1. Тогда 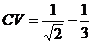и


где CD perpendikulyarVU. Учительница не сможет добежать до вершины V раньше, чем мальчик доплывёт до точки D:

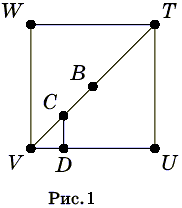
Ответ. да, сможет.

Задача №22

Посередине, между двумя параллельными улицами стоят в один ряд одинаковые дома со стороной, равной a. Расстояние между улицами — 3a, а расстояние между двумя соседними домами — 2a. Одна улица патрулируется полицейскими, которые движутся на расстоянии 9a друг от друга со скоростью v. К тому времени, как первый полицейский проходит мимо середины некоторого дома, точно напротив него на другой улице появляется гангстер. С какой постоянной скоростью и в какую сторону должен двигаться по этой улице гангстер, чтобы ни один полицейский его не заметил?

Решение

Проведем две прямые x и y параллельно улицам через края домов (считаем, что прямая x ближе к той улице, на которой стоят полицейские). Соединим точку, в которой находится гангстер, отреками со всеми точками, в которых находятся полицейские. Занумеруем эти отрезки целыми числами от -¥ до +¥ в том порядке, в котором расположены полицейские на первой улице. Пусть xi и yi – точки, в которых i -й отрезок пересекает прямые x и y . Достаточно доказать, что если ни одна из точек x0 и y0 не остается неподвижной, то полицейские обязательно увидят гангстера. Предположим, что точки x0 и y0 движутся (тогда движутся и все остальные точки). Рассмотрим большой отрезок времени t . В течение времени T более половины времени точка x0 и не лежала на сторонах домов, и более половины времени точка y0 не лежала на сторонах домов. Тогда найдется момент времени, когда ни одна из точек x0 и y0 не лежала на сторонах домов. Докажем, что в этот момент один из полицейских видит гангстера. Рассмотрим тот отрезок прямой x между домами, на котором находится точка x0 . Точки xi расположены с интервалом 6a , а точки yi – с интервалом 3a . Поэтому на отрезке прямой y , расположенном напротив рассматриваемого отрезка прямой x найдется точка yi с некоторым номером i . Тогда полицейский с номером -i видит гангстера.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7