Задачи обучающего тура (стр. 2 )

Подсказка

Всего кофе в двух стаканах столько же, сколько молока.

Решение

Примем начальный объем жидкости в каждом стакане за 1. Таким образом, после всего в обоих стаканах имеется единичный объем кофе и единичный объем молока. Поскольку из первого стакана перелили во второй одну ложку, а затем из второго в первый перелили такую же ложку, то в конце в каждом стакане снова будет объем жидкости, равный 1. Пусть объем кофе в первом стакане после переливания равен x, а во втором стакане - y. Тогда молока во втором стакане - (1-y). Поскольку в двух стаканах всего единичный объем кофе, x+y=1. Отсюда x=1-y, т. е. кофе в стакане с молоком и молока в стакане с кофе поровну.

Ответ. Поровну

Задача №12

У Алёны есть мобильный телефон, заряда аккумулятора которого хватает на 6 часов разговора или 210 часов ожидания. Когда Алёна садилась в поезд, телефон был полностью заряжен, а когда она выходила из поезда, телефон разрядился. Сколько времени она ехала на поезде, если известно, что Алёна говорила по телефону ровно половину времени поездки?

Решение

Первое решение. Во время разговора энергия аккумулятора расходуется в 210/6=35 раз быстрее, чем в то время, когда разговор не ведётся. Пусть Алёна проговорила x часов. Тогда энергии аккумулятора осталось на (6-x) часов разговора или на 35 ∙  (6-x) часов ожидания. По условию это время также равно x часов ожидания, поэтому 35 ∙  (6-x)=x, откуда x=35 ∙ 6/36=35/6 часов, то есть 5 ч 50 мин. И, значит, вся поездка продолжалась 11 ч 40 мин.

Второе решение. Если бы Алёна говорила 210 ∙ 6 часов и молчала 210 ∙ 6 часов, то телефон бы полностью разрядился 210+6=216 раз. Так как на на самом деле телефон разрядился один раз, Алёна говорила 210 ∙ 6/216 часов и молчала 210 ∙ 6/216 часов, то есть ехала она 2 ∙  (210 ∙ 6/216) часов. После сокращения получаем 11 часов 40 минут.
Примечание. Ответ в этой задаче является средним гармоническим чисел 6 и 210 (средним гармоническим чисел a и b называется число 2/((1/a)+(1/b))=2ab/(a+b)).

Ответ. 11 часов 40 минут.

Задача №13

От двух кусков сплавов (с различным содержанием свинца) массой в 6 и 12 кг отрезали по куску равной массы. Каждый из отрезанных кусков сплавили с остатком другого куска, после чего процентное содержание свинца в обоих сплавах стало одинаковым. Каковы массы каждого из отрезанных кусков?

Решение

Пусть x – процентное содержание свинца в первом сплаве, y – процентное содержание свинца во втором сплаве. Пусть от каждого куска отрезали по z кг и прибавили столько же килограммов другого сплава. Тогда процентное содержание свинца в первом куске стало:

( ((6-z)x)/100+yz/100)·100/6=(6x-zx+yz)/6.

Процентное содержание свинца во втором куске:

( ((12-z)y)/100+xz/100)·100/12=(12y-zy+xz)/12.

Получаем уравнение 2(6x-zx+yz)=12y-zy+xz , 12(x-y)-3z(x-y)=0 , z=4 .

Ответ. 4 кг.

Задача №14

После ведения санитарной обработки на базе отдыха количество мух уменьшилось на 9%, а количество комаров – на 4%. В целом количество насекомых уменьшилось на 5%. Сколько процентов от общего числа насекомых составляли комары?

Решение:

Пусть х – было мух, у - было комаров.

0.91х – стало мух после обработки.

0.96у – стало комаров после обработки

0.95(х+у) – стало насекомых после обработки.

Уравнение:

0.91х+0.96у=0.95(х+у)

0.91х+0.96у=0.95х+0.95у

0.96у-0.95у=0.95х-0.91х

0.01у=0.04х

у=4х – следовательно, комаров 80 % от общего числа насекомых

Ответ: 80%

Задача №15

Известно, что вклад, находящийся в банке, с начала года возрастает к концу года на определённый процент (свой для каждого банка). В начале года 5/6 некоторого количества денег положили в первый банк. К концу года сумма этих вкладов стала равной 670 у. е., а к концу второго года – 749 у. е. Было подсчитано, что если бы первоначально исходное количество денег положили во второй банк, то по истечении одного года сумма вкладов в эти банки стала бы равной 710 у. е. В предложении, что исходное количество денег первоначально целиком положено в первый банк, определить величину вклада по истечении двух лет.

Решение.

Обозначим через x первоначальную сумму денег. Тогда через а обозначим процент, на который возрастает сумма за год в первом банке, а через b – во втором банке. К концу первого года сумму вклада в I банке стала равной , во II банке , а к концу второго года и . По условию задачи сумма вкладов в конце первого года составляет 670 у. е., а к концу второго года – 749 у. е., поэтому можно составить два уравнения:

Если во второй банк положить у. е., а в первый – у. е, то сумма вкладов к концу года составила бы:

,

что равнялось бы 710 у. е. Поэтому получим третье уравнение:

Для нахождения известного х составим систему уравнений из (1) и (3) и решим её (4а).

Подставляя вместо и вместо в уравнение (2), приходим к уравнению (рис. 4б), имеющему один корень: x=660, но тогда:

Если исходное количество денег положить на два года, то к концу второго года величина вклада составит 726 у. е.

Ответ.726 у. е.

Задача №16

Трое рабочих копают яму. Они работают по очереди, причем каждый из них работает столько времени, сколько нужно двум другим, чтобы вырыть половину ямы. Работая таким образом, они выкопали яму. Во сколько раз быстрее трое рабочих выкопают такую же яму, если будут работать одновременно?

Решение

Первый способ.

Пусть время работы каждого из рабочих составляет a, b и c часов соответственно. Следовательно, яма была выкопана за a + b + c часов.

В случае совместной работы: за первые a часов первый рабочий выкопает свою долю от "общей" ямы, а двое других могли бы выкопать еще половину ямы. За следующие b часов свою часть работы сделает второй, а остальные также могли выкопать половину ямы. И, наконец, за c часов третий рабочий сделает свою часть работы, а двое остальных — еще половину ямы.

Следовательно, за a + b + c часов могло быть выкопано 2,5 ямы. Значит, работая одновременно, они выкопали бы такую же яму в 2,5 раза быстрее.
Второй способ.

Пусть производительность каждого из рабочих равна x, y и z ям за час соответственно. Тогда время работы каждого из них соответственно равно: , и часов. То есть, они выкопали яму за время T = + + (часов). При этом, первый рабочий выкопал ямы, второй — ямы, а третий — ямы. Так как, работая таким образом, они выкопали яму, то + + = 1. В случае совместной работы, время выкапывания ямы составит: 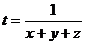часов. Используя это, преобразуем составленное уравнение: + + = 2 Û+ 1 + + 1 + + 1 = 2 + 3 Û+ + =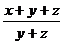

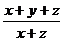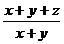Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7