Задачи обучающего тура (стр. 7 )

Обозначим расстояние между соседними поездами через l. Если в некоторой точке X лес, то в точке Y, находящейся от нее на расстоянии, кратном l, тоже лес. Действительно, если Ира входит на станцию, когда Рома находится в точке X, то она уедет первой. Но когда Рома находится в точке Y, расположение поездов такое же, как когда он находится в точке X, так что в этом случае Ира тоже уедет первой, поэтому в точке Y тоже лес.

Итак, "структура" леса периодическая, поэтому достаточно определить расположение леса на интервале длины l.

Рассмотрим момент, когда некоторый поезд отходит от станции B (рис.). Пусть поезд, на который сядет Ира

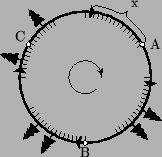
(т. е. ближайший против направления движения к станции A поезд) в этот момент находится на расстоянии x от A. Тогда весь интервал между этим поездом и точкой A покрыт лесом. Действительно, если машинист Рома находится на этом интервале, то он увезет Иру, потому что Лёша "упустил" свой поезд (строго говоря, это следует из того, что x < l).

Покажем, что интервал длины l - x, следующий за A по направлению движения, лесом не покрыт. Действительно, когда поезд придет на станцию A, то ближайший к B против направления движения поезд будет на расстоянии l - x. Так что если Рома находится на указанном интервале длины l - x, то Лёша сядет в поезд первым, так как Ира "упустила" поезд, который ведет Рома.

Итак, на участке длины l леса — x, а поля — l - x. Так как структура леса периодическая, то и на всей дороге количество леса относится к количеству поля как x к l - x.

Осталось найти x. Длина окружности равна nl, значит, длина большей дуги BA равна nl. Ясно, что величина x равна остатку от деления длины дуги BA на l. Значит, если остаток от деления n на 3 равен 1, то x = , т. е. доля леса составляет .

Аналогично, если остаток от деления n на 3 равен 2, то x = , и лес составляет .

Ответ. 1/3

Задача №41

Ширина реки один километр. Это по определению означает, что от любой точки каждого берега можно доплыть до противоположного берега, проплыв не больше километра.
Может ли катер проплыть по реке так, чтобы в любой момент расстояние до любого из берегов было бы не больше:

а)(4) 700 м?

б)(4) 800 м?

(Берега состоят из отрезков и дуг окружностей.)  

Решение

а) Ответ: не всегда. Отсутствие такого маршрута вытекает из рисунка 1. Маршрут катера должен пересекать отрезок AB. Тогда расстояние от любой точки AB до одного из берегов больше 700 м.

б) Ответ: всегда. Построим такой маршрут. Выберем часть плоскости по одну сторону от правого берега, содержащую левый берег, и рассмотрим множество точек, удалённых от правого берега не более чем на 800 м. Построить его можно так: возьмём красящий круг радиусом 800 м и протащим его центр вдоль правого берега. Тогда круг закрасит полосу, граница которой тянется вдоль реки (обозначим эту границу через L).
Если L вся идёт по суше, то левый берег даст искомый маршрут. Если L — вся на воде, то рассмотрим L в качестве маршрута. Если L пересекает левый берег, то участки L вне реки заменим участками левого берега и рассмотрим полученный маршрут. Каждая точка такого маршрута отстоит от правого берега не больше чем на 800 м. Докажем, что и от левого берега тоже.

Допустим, что это неверно, т. е. найдётся точка на маршруте, удалённая от левого берега больше чем на 800 м. Тогда круг с центром в этой точке и радиусом 800 м целиком лежит на воде (кроме одной или нескольких точек правого берега на окружности). Докажем, что тогда найдётся точка на одном из берегов, расстояние от которой до другого берега больше 1000 м.

Рассмотрим множество лучей с началом в центре O этого круга и покрасим их в два цвета: в синий цвет, если первое пересечение луча происходит с правым берегом, и в красный — если с левым. Соответственно покрасим точки окружности. Покажем, что найдётся одноцветная дуга окружности величиной не меньше 180o. Для этого докажем, что окружность состоит не больше чем из двух разноцветных дуг.

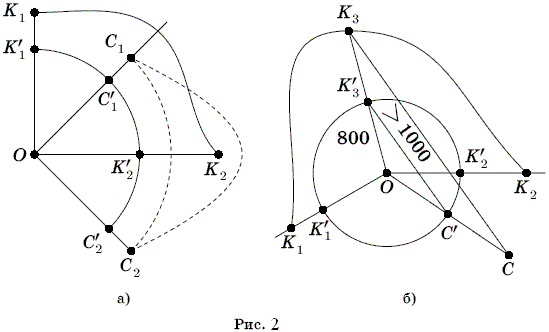
Допустим, что это неверно и разноцветных дуг больше двух. Поскольку дуги чередуются, то их чётное число. Возьмём по одной точке на четырёх соседних дугах: красную К'1, синюю С'1, красную К'2, синюю С'2, и соответствующие им точки первого пересечения лучей с берегами: К1, С1, К2, С2 (рис. 2а).
Береговая линия между К1 и К2 должна пересекать один из лучей OС1, OС2 (пусть ОС1), причём дальше от центра, чем С1. Рассмотрим контур, состоящий из береговой линии между К1 и К2 и отрезков OК1 и OК2. Этот контур разделяет точки С1 и С2, поэтому береговая линия между С1 и С2 должна его пересечь, но это невозможно (поскольку берега не пересекаются и есть правило раскраски). Следовательно, дуг ровно две, так как из точки О видны оба берега, а тогда найдётся одноцветная дуга (пусть красная) не меньше 180o.

Возьмём концы этой дуги К'1, К'2, её середину К'3 и соответствующие точки берега К1, К2, К3 (рис. 2б).

Построим контур, состоящий из береговой линии между К1 и К2 и отрезков OК1 и OК2. Кратчайший путь от К3 до другого берега пересекает один из отрезков OК1, OК2. Следовательно, этот путь будет виден из точки O под углом не меньше 90o, но такой путь с концами вне круга будет не короче м > 1000 м. Это противоречит условию.
Итак, круг с центром на указанном маршруте радиусом 800 м поместить между берегами невозможно, поэтому всегда будет точка левого берега, отстоящая от указанного маршрута меньше чем на 800 м.

Задача №42

В классе 30 учеников, и у каждого из них одинаковое число друзей среди одноклассников. Каково наибольшее возможное число учеников, которые учатся лучше большинства своих друзей? (Про любых двух учеников в классе можно сказать, кто из них учится лучше; если A учится лучше B , а тот – лучше C, то A учится лучше C.)

Решение

Учеников, которые учатся лучше большинства своих друзей, назовем хорошими. Пусть x – число хороших учеников, k – число друзей у каждого ученика. Лучший ученик класса является лучшим в k парах друзей, а любой другой хороший ученик – не менее, чем в парах (здесь квадратные скобки обозначают целую часть числа). Поэтому хорошие ученики являются лучшими не менее, чем в парах. Это число не может превышать числа всех пар друзей в классе, равного . Отсюда , или

Заметим далее, что

поскольку число учеников, лучше которых учится наихудший из хороших учеников, не превышает 30-x. Правая часть неравенства (1) возрастает с ростом k, а неравенство (2) равносильно условию

Из (1) и (3) следует, что 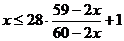, или

Наибольшим целым x, удовлетворяющим (4) и условию , является x=25 . Итак, число хороших учеников не превышает 25.

Покажем, что оно может равняться 25. Занумеруем учеников числами от 1 до 30 в порядке ухудшения успеваемости и расположим номера в таблице 6x 5 так, как показано на 108. Пусть пара учеников является парой друзей, если их номера расположены одним из трех способов: а) в соседних строках и в разных столбцах; б) в одном столбце и один из номеров при этом находится в нижней строке; в) в верхней строке. При этом, как нетрудно проверить, все требуемые условия выполнены.

Ответ. 25.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7