Задачи обучающего тура (стр. 6 )

Тогда искомое отношение скоростей мотоциклистов А и С равно .

Ответ.

Задача №33

Стива Облонский и Васенька Весловский поехали на охоту. Спустя некоторое время вслед за ними отправился Константин Дмитриевич Левин. Через час после своего выезда Левин находился на равном расстоянии от Облонского и Васеньки, а еще через 1,5 ч, обогнав обоих, Левин был в 8 раз дальше от Стивы, чем от Васеньки. Найдите, через сколько времени после выезда Облонского и Весловского выехал Левин, если он догнал Васеньку через 3 ч после выезда своих гостей.

Решение:

Изобразим графики движения: Облонского – OS; Весловского – OV; Левина – KL (рис. 2). отправился через х ч после своих гостей (ОК = х). Через час (КМ = 1) Левин находился на равном расстоянии от Облонского и Васеньки (АВ = ВС = z). Через 3 ч после выезда гостей Левин обогнал Васеньку (МР = ОР – ОМ = 2 – х), а еще через 1,5 ч, обогнав обоих, Левин был в 8 раз дальше от Стивы, чем от Васеньки (PN = MN – MP =1,5 – (2 - x) = x – 0,5, LV = y, VS = 7y).

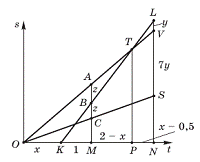
(рис 2.)

Из подобия треугольников АОС и VOS, AOM и VON следует, что

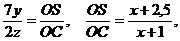
Откуда

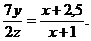
Из подобия треугольников LTV и BTA и теоремы о пропорциональных отрезках следует, что 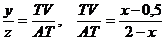, откуда

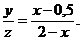
Из равенств (1) и (2) следует, что

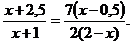
Уравнение (3) имеет единственный положительный корень 1, следовательно, Левин выехал через 1 ч после выезда своих гостей.

Ответ. Левин выехал через 1 ч после выезда своих гостей.

Подсказка.

Допустим, что в каждом регионе все получают одинаковую зарплату и есть регион, в котором живут те самые 10% работников, которые получают 90% всей зарплаты.

Ответ: да, может.

Задача №35

По неподвижному эскалатору человек спускается быстрее, чем поднимается.
Что быстрее: спуститься и подняться по поднимающемуся эскалатору или спуститься и подняться по спускающемуся эскалатору? (Предполагается, что все скорости, о которых идет речь, постоянны, причём скорости эскалатора при движении вверх и вниз одинаковы, а скорость человека относительно эскалатора всегда больше скорости эскалатора.)  

Решение

Обозначим скорость эскалатора через v, скорости человека, поднимающегося и спускающегося по эскалатору, через v1 и v2 соответственно (тогда v < <v1 < v2). Длину эскалатора обозначим через l. Тогда время движения по поднимающемуся эскалатору равно
t1 = l / (v1 + v) + l / (v2 – v),

а по спускающемуся эскалатору –

t2 = l /(v2 + v) + l / (v1 – v).

Вычислим разность

t1 – t2 = l / (v1 + v) + l / (v2 – v) – l / (v2 + v) – l / (v1 – v) = 2lv (1 / (v22 – v2) – 1 / v12 – v2).
По условию, знаменатели обеих дробей положительны, причём первый больше второго, поэтому всё выражение отрицательно. Вывод: t1 < t2.

Ответ. Быстрее спуститься и подняться по поднимающемуся эскалатору.

Задача №36

109 яблок разложены по пакетам. В некоторых пакетах лежит по x яблок, в других по 3 яблока. Найдите все возможные значения x, если всего пакетов - 20.

Решение

Первое решение. Если бы в каждом пакете было по 3 яблока, то всего яблок было бы 60, но на самом деле яблок на 49 больше. Значит, "лишние" яблоки надо распределить поровну по некоторым пакетам. Так как 49 = 7 . 7 = 49 . 1 и всего пакетов - 20, то либо в 7 пакетах содержится по 7 "лишних" яблок, либо в одном пакете 49 "лишних" яблок. В первом случае x = 10, а во втором случае x = 52.

Второе решение. Пусть есть n пакетов, в которых лежит по 3 яблока. Тогда количество пакетов, в которых находится по x яблок, равно 20 - n. Из условия следует, что 3n + x(20 - n) = 109. Преобразуем полученное уравнение так, чтобы его левую часть можно было разложить на множители: 20x + 3n – nx - 60 = 49Û20(x - 3) - n(x - 3) = 49Û (x - 3)(20 - n) = 49. Отсюда получим, что

x=10, n=13 или x=52, n=19.

Ответ. 10 или 52.

Задача №37

Клиент хочет купить квартиру, стоимость которой 1 300 000 рублей. Эту квартиру одобрил банк. Независимый оценщик может определить её рыночную стоимость, которая будет оплачиваться от той, которую определил продавец. Допустим, оценщик оценил её в 100 000 рублей. На какую сумму может рассчитывать клиент, если банк предоставляет ипотечный кредит 70% от оценочной стоимости квартиры. (700 000 рублей). Сколько всего заплатит клиент банку через 10 и 15 лет под 16 % годовых, равномерно погашая кредит с уплатой процентов на остаток задолженности?

Решение:

используем формулу

Sn = So(1 + 0,01pn ) - 0,5 (0,01p × So (n – 1)),

10 лет:

S = 700 000 (1 + 0,01×16 × 10) - 0,5 (0,01×16 × 700 000 ×9) = 1 316 000 рублей;

15 лет:

S = 700 000 (1 + 0,01×16 × 15) - 0,5 (0,01×16 × 700 000 ×14) = 1 596 000 рублей.

Ответ: через 10 лет клиент заплатит банку 1 316 000 рублей; через 15 лет – 1 596 000 рублей.

Задача №38

Имеется два трёхлитровых сосуда. В одном 1 л воды, в другом - 1 л двухпроцентного раствора поваренной соли. Разрешается переливать любую часть жидкости из одного сосуда в другой, после чего перемешивать. Можно ли за несколько таких переливаний получить полуторапроцентный раствор в том сосуде, в котором вначале была вода?

Решение

Обозначим через an и bn концентрации растворов в первом и втором сосудах после n переливаний соответственно (a0 = 0, b0 = 0,02). Можно считать, что в процессе переливаний мы не опустошаем сосуды. Пусть an – 1 < bn – 1. Если мы теперь перельём раствор из первого сосуда во второй, то получим an = an – 1 < bn. А если мы перельём раствор из второго сосуда в первый, то получим an < bn – 1 = bn. Таким образом, неравенство сохраняется. Пусть an = 0,015. Тогда bn > 0,015. Перельём всё в один сосуд и перемешаем. Получится, что концентрация всего раствора больше 0,015, в то время как она в точности равна 0,01.

Ответ. Можно

Задача №39

Гриша едет по маршруту длиной 100 км. В его автомобиле имеется компьютер, дающий прогноз времени, оставшегося до прибытия в конечный пункт. Это время рассчитывается исходя из предположения, что средняя скорость автомобиля на оставшемся участке пути будет такой же, как и на уже пройденном.

Сразу же после старта компьютер показал "2 часа" и всё дальнейшее время показывал именно это число (компьютер исправен). Найдите x(t) — зависимость пути, который проехал Гриша, от времени с момента старта. Постройте график этой зависимости.

Решение

Через t часов с момента старта Гриша проедет x(t) километров. Его средняя скорость составит x(t)/t км/ч. Оставшиеся 100 - x(t) км Гриша, по мнению компьютера, будет двигаться с той же средней скоростью, то есть проедет этот участок за (100 - x(t)) / (x(t)/t) ч, что по условию всегда составляет 2 ч. Тогда (100 - x(t))(x(t) / t) = 2, то есть x(t) = 100t / (t + 2), t > 0. Это и есть искомая зависимость.

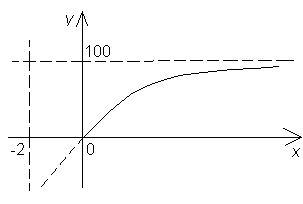
Для построения графика преобразуем: 100t / (t + 2) = (100(t + 2) - 200) / (t + 2) = 100 - 200 / (t + 2), t > 0. Графиком функции x(t) = 100 - 200 / (t + 2), где t > 0, является часть гиперболы x(t) = -200 / t, смещённой на 2 влево и на 100 вверх. Схематичный график зависимости пройденного расстояния от времени приведён на рисунке.

Ответ.

Задача №40

По окружности в одном направлении на равных расстояниях курсируют n поездов. На этой дороге в вершинах правильного треугольника расположены станции A, B и C (обозначенные по направлению движения). Ира входит на станцию A и одновременно Лёша входит на станцию B, чтобы уехать на ближайших поездах. Известно, что если они входят на станции в тот момент, когда машинист Рома проезжает лес, то Ира сядет в поезд раньше Лёши, а в остальных случаях Лёша — раньше Иры или одновременно с ней. Какая часть дороги проходит по лесу?

Решение

Для ясности будем считать поезда и станции точками.

Понятно, что если n делится на 3, то Лёша и Ира всегда уезжают одновременно. Значит, в этом случае лес отсутствует. Пусть n не делится на 3. Тогда, когда бы они ни пришли на станцию, либо Ира уедет раньше Лёши, либо - Лёша раньше Иры.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7