Но величина F·Dl есть объем газа (DV), прошедшего через выделенные сечения за время Dt. Тогда:
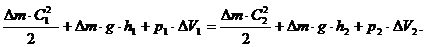
Умножив обе части равенства на величину ![]() и принимая во внимание, что
и принимая во внимание, что ![]() , получим:
, получим:
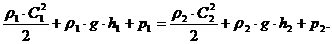 (14)
(14)
Или:
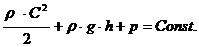 (15)
(15)
Это уравнение и получило наименование «уравнение Бернулли». В таком виде оно без ограничений применимо для жидкостей и с минимальными погрешностями может использоваться для газов, движущихся с небольшими скоростями.
Применительно к ТВаД уравнение (15) можно упростить. Т. к. газ в двигателе движется по горизонтально расположенному каналу небольшой протяженности и плотность газа на входе в двигатель незначительно отличается от плотности на выходе, можно допустить, что r·g·h = const. Тогда формула (15) примет вид:
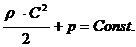 (16)
(16)
В формуле (16) величина ![]() называется динамическим давлением, т. е. давлением, обусловленным скоростным напором,
называется динамическим давлением, т. е. давлением, обусловленным скоростным напором, ![]() — как было сказано в п.2.2., статическое давление.
— как было сказано в п.2.2., статическое давление.
Из формулы (16) можно сделать вывод, что при движении газа по каналам при росте скорости потока будет происходить падение давления газа и наоборот.
2.6 Параметры заторможенного потока
Для решения практических задач с помощью выше приведенных формул, должны быть известны статические параметры состояния газа. Для того чтобы измерить эти параметры в движущемся газе, датчики приборов должны, двигаться со скоростью, равной скорости потока. Такой способ измерения параметров весьма затруднителен.
В реальном двигателе датчики давления и температуры газа закреплены неподвижно в канале и находятся под действием скоростного напора Движущийся газ, сталкиваясь с неподвижным датчиком прибора, затормаживается, что приводит к завышенным показаниям термометров и манометров.
В связи с этим возникла необходимость, введения новых параметров, так называемых параметров заторможенного потока.
*Для сравнительно небольших скоростей потока, которые имеют место в ТВаД, изменением внутренней энергии газа можно пренебречь.
Параметрами заторможенного потока называются параметры газа после его адиабатического торможения до нулевой скорости.
Параметры заторможенного потока часто называют полными параметрами газа и обозначают теми же буквами, что и статические, но со звездочкой вверху (например, р*, Т* и т. д.). Очевидно, что С*= 0
Параметры заторможенного потока замерить практически значительно легче. Для определения всех параметров потока следует установить зависимость между параметрами заторможенного потока и статическими параметрами.
Величину полного давления можно определить из уравнения Бернулли. Если в формуле (16) принять С=0, т. е. затормозить поток до нулевой скорости, то получим:
![]()
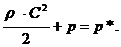 (17)
(17)
Т. е., можно сказать, что полное давление газа есть сумма статического (р) и динамического (![]() ) давлений.
) давлений.
Однако формулой (17) в инженерных расчетах пользоваться неудобно, кроме того, эта формула для больших скоростей газа дает существенные погрешности. Поэтому для практического использования в термодинамических расчетах применяются другие формулы:
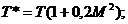 (18)
(18)
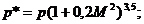 (19)
(19)
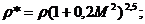 (20)
(20)
Где Т*, р*, r* — температура, давление и плотность заторможенного потока;
М— число Маха, равное отношению скорости газа к местной скорости звука (М=С/а).
Используя формулы (18) — (20) можно, зная статические параметры газа и скорость его движения, рассчитать полные параметры и наоборот. Из этих формул видно, что параметры заторможенного потока будут численно всегда больше статических.
2.7. Изменение параметров газа при его движении в канале*
Используя ранее полученные выводы, рассмотрим, как будут изменяться параметры газа при его движении в сужающемся расширяющемся каналах. Такие каналы называются соответственно конфузор и диффузор (рис.14).
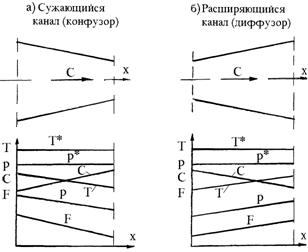
![]() Рис.14. Изменение параметров газа при его движении в сужающемся (а) и расширяющемся (б) каналах
Рис.14. Изменение параметров газа при его движении в сужающемся (а) и расширяющемся (б) каналах
При движении газа в сужающемся канале (F¯) согласно уравнению неразрывности (п.2.4) происходит рост скорости течения газа (С ). Так как скорость возрастает, то согласно уравнению Бернулли (п.2.5), статическое давление газа снижается (р¯). При снижении статического давления, согласно уравнения состояния (п.2.1), происходит снижение статической температуры газа (Т¯).
* Приведенные выводы справедливы только для газа, движущегося с дозвуковой скоростью.
При движении газа в расширяющемся канале все параметры по тем же причинам изменяются, но их изменение противоположно по знаку, т. е. С¯, р , Т.
Параметры заторможенного потока при движении газа в каналах в случае отсутствия потерь энергии остаются постоянными. Это объясняется тем, что изменение статической и динамической составляющей параметра противоположны по знаку (см. формулы 18—20) и уменьшение одной величины компенсируется ростом второй и наоборот. В реальных каналах из-за неизбежности потерь происходит некоторое снижение величин Т*, р*.
2.8. Уравнение Эйлера*
Уравнение, полученное членом Российской Академии наук, Леонардом Эйлером (1707—1783), позволяет определить силу «Р», с которой движущийся газ действует на стенки каналов и другие поверхности, ограничивающие его объем. Уравнение Эйлера является следствием второго и третьего законов Ньютона применительно к движущимся газам.
Для вывода уравнения Эйлера возьмем произвольную струйку тока и ограничим рассматриваемый нами объем воздуха сечениями «1» и «2» (рис.15).
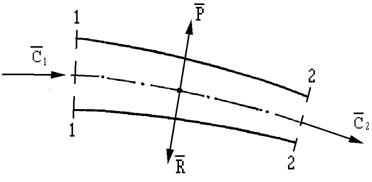
Рис.15. К выводу уравнения Эйлера
Газ в сечении «1» имеет скорость С1 и в сечении «2» — С2. Векторы скоростей С1 и С2 не равны по модулю и не параллельны. Следовательно, газ, проходя по струйке тока, двигается с ускорением. Согласно второму закону на любое материальное тело массой «m», движущееся с ускорением «a» должна действовать сила «R», которая определяется по формуле:
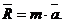 (21)
(21)
Учитывая, что ![]()
где Dt — время, за которое газ пройдет от сечения «1» до сечения «2»
можно записать:
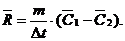 (22)
(22)
Но величина ![]() есть масса газа, проходящего через произвольное сечение трубки тока в единицу времени. Эта величина называется расходом газа G=
есть масса газа, проходящего через произвольное сечение трубки тока в единицу времени. Эта величина называется расходом газа G=![]() . Тогда формула (22) примет вид:
. Тогда формула (22) примет вид:
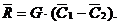 (23)
(23)
Из третьего закона Ньютона следует, что сила действия равна по величине и противоположна по направлению силе противодействия. Откуда: 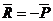 , следовательно:
, следовательно:
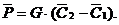 (24)
(24)
Формула (24) получила наименование уравнения Эйлера. Из анализа уравнения Эйлера можно сказать, что сила, с которой движущейся газ действует на стенки каналов и другие поверхности, ограничивающие его объем, равна произведению расхода газа на векторную разность скоростей в сечениях на выходе и входе.
* В данном пособии приведено в упрощенном виде.
2.9. Политропическая работа движущегося газа.
Политропическая работа движущегося газа «Lпол» представляет собой сумму политропической работы расширения (сжатия) «Lрасш» неподвижного газа и работы на проталкивания газа в канале «Lпрот».
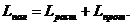 (25)
(25)
Для рассмотрения факторов, влияющих на величину политропической работы движущегося газа, выберем произвольную струйку тока, ограниченную сечениями «1» и «2» (рис.16). В сечении «1» площадь струйки F1 , давление газа р1., скорость С1 , в сечении «2» соответственно F2, , р2, С2.
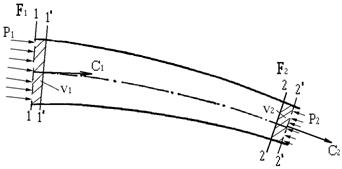
Рис. 16. К пояснению политропической работы движущегося газа
За произвольный интервал времени «t» газ переместится вдоль канала и займет положение, соответствующее сечениям 1' и 2'. Между этими сечениями будет заключен газ объемом соответственно V1 и V2. В общем случае, эти объемы не равны между собой (V1 ¹ V2), поэтому можно сказать, что газ перемещаясь из сечения «1» в сечение «2» расширяется (или сжимается).
В термодинамике, как правило, определяют политропическую работу движущегося газа, отнесенную к единице массы, поэтому в дальнейшем вместо абсолютного объема газа «V» ,будем рассматривать объем единицы массы газа, т. е. удельный объем «v». Тогда работа расширения единицы массы неподвижного газа может быть определена по формуле:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |



