Рис.9. Области применения газотурбинных двигателей по скорости и высоте полета:
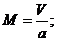Где: V — скорость полета; 
— скорость звука; Н — высота полета
* Имеются газотурбинные двигатели со свободной турбиной, которые устанавливаются на самолеты. В этом случае мощность со свободной турбины передается на тянущий воздушный винт. Например, двигатели: ТВ7-117 (самолет Ил-114), М-601Е (самолет Л-410), ТВД-1500 (самолет Ан-38). Такие двигатели, как и другие, устанавливаемые на самолеты и вращающие воздушный винт, называются турбовинтовыми (ТВД).
Летно-технические характеристики конкретных летательных аппаратов могут отличаться от приведенных на рисунке 9. Это может объясняться особенностями аэродинамической компоновки ЛА, характеристиками материалов, из которых изготовлен планер, назначением ЛА, КПД воздушных винтов и др.
2. ОСНОВНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ ТЕРМОДИНАМИКИ И ГАЗОВОЙ ДИНАМИКИ
Как видно, в газотурбинных двигателях всех типов, тяга (мощность) образуется при прохождении газа через проточную часть двигателя. При этом изменяются параметры газа: давление, температура, скорость и др. Поэтому для понимания процессов, происходящих в двигателе, и природы возникновения тяги (мощности) необходимо использовать законы термодинамики и газовой динамики. Ниже будут кратко рассмотрены основные понятия и уравнения термодинамики и газовой динамики, применительно к процессам, происходящим в ТВаД.
2.1. Уравнение состояния газа
Это уравнение читается так: при любом состоянии данного идеального газа произведение его давления на удельный объем равно произведению газовой постоянной на абсолютную температуру. Или:
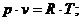(1)
где: р— давление газа;
v— удельный объем газа;
Т— абсолютная температура газа;
R— газовая постоянная (для воздуха R=29,27 кг/кгс·град)
Иногда уравнение состояния газа записывается в виде:
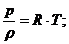(2)
где: 
— плотность газа.
Уравнение состояния газа было получено для неподвижного газа, имеющего постоянную массу. Поэтому величины р,. v и Т называются статическими параметрами газа. Однако этим уравнением можно пользоваться и при определении изменения параметров движущегося газа. Для этого необходимо выделить в потоке газа какой-либо его объем и следить за изменением его состоянием по мере продвижения газа по проточной части канала, при этом масса газа внутри выделенного объема должна оставаться неизменной.
Применяя уравнения состояния к ТВаД необходимо иметь в виду, что во всех узлах ТВаД, кроме камеры сгорания, удельный объем газа изменяется менее интенсивно, чем остальные параметры. Потому при повышении давления газа неизменно будет возрастать и его температура. В камере сгорания за счет значительного подвода тепла будет происходить рост удельного объема и температуры газа при незначительном изменении давления.
2.2. Основные термодинамические процессы
Как было сказано выше, состояние газа характеризуется определенными параметрами, причем эти параметры могут изменяться.
Если в процессе изменения параметров газа :
v = const — процесс называется изохорическим;
Т = const — процесс называется изотермическим;
р = const — процесс называется изобарический.
Если в процессе изменения параметров газа к нему не подводится и от него не отводится тепловая энергия, такой процесс называется адиабатический и для него выполняется условие:
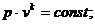(3)
где: к— показатель адиабаты (для воздуха к = 1,4).
Произвольный термодинамический процесс называется политропическим и для него справедливо условие:
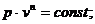(4)
где: n— показатель политропы.
В ТВаД, если не учитывать потери тепла, можно считать, что во всех узлах, кроме камеры сгорания, имеет место адиабатический процесс. В реальности в компрессоре и турбине имеют место политропические процессы с показателем политропы:
— для компрессора 1,47…1,5;
— для турбины 1,27… 1,33.
В камере сгорания процесс максимально приближенный к изобарическому.
2.3. Линия тока, трубка тока, струйка
В установившемся потоке газа каждая его частица движется по определенной траектории, которая представляет собой линию (рис.10). В каждой точке этой линии касательная к ней параллельна вектору скорости. Такая линия называется линией тока.
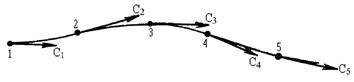
Рис.10. Линия тока
Если выделить поперек потока маленькую площадку произвольного очертания и через все точки контура провести линии тока, то последние образуют некоторую цилиндрическую поверхность, называемую трубкой тока. Масса жидкости, заключенная в трубке тока, образует струйку (рис.11).
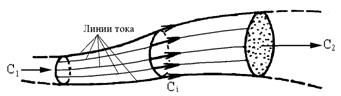
Рис.11. Трубка тока, струйка
Таким образом можно сделать вывод, что струйка является элементарным потоком газа. Для струйки справедливо:
— скорость газа во всех точках одного поперечного сечения считается величиной постоянной;
— через границы струйки (через трубку тока) не происходит переноса массы газа.
Газ во внутренних объемах ГТД движется по каналам ограниченным твердыми стенками и имеющим сравнительно небольшую площадь поперечного сечения. Такой поток условно можно считать струйкой и распространять на него все закономерности, характерные для струйки.
2.4. Уравнение неразрывности
Уравнение неразрывности устанавливает зависимость между площадью поперечного сечения струйки (F), скоростью газа (C) и его плотностью (r). Это уравнение можно сформулировать так: при установившемся движении газа произведение площади поперечного сечения струйки на скорость и плотность газа является величиной постоянной и одинаковой для всех сечений струйки.
Для доказательства этого выделим в потоке газа произвольную струйку (рис.12).
Рис. 12. К выводу уравнения неразрывности
Так как через границы струйки не происходит перетекания, то можно сказать, что в единицу времени через каждое сечение струйки пройдет одинаковая масса газа. Через сечение «1» в единицу времени пройдет масса газа:
.
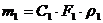Где: С1 — скорость движения воздуха через сечение «1» струйки;
F1 — площадь поперечного сечения струйки в сечении «1»;
r1 — плотность воздуха в сечении «1».
Следовательно можно записать:
m1 = m2
или
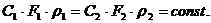(5)
В ТВаД плотность газа изменяется в меньшей степени, чем остальные параметры. Поэтому условно можно принять r=const, и тогда уравнение (5) примет вид:
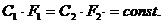(6)
Из уравнения (6) можно сделать вывод: чем меньше площадь канала, тем больше скорость течения газа.
2.5. Уравнение Бернулли
Уравнение Бернулли является следствием закона сохранения энергии газа в струйке тока, оно названо по имени академика Петербургской Академии наук Даниила Бернулли, сформулировавшего его в 1738 г.
Выделим в установившемся потоке газа произвольную струйку (рис.13). Пусть в сечении струйки «1» трубка тока имеет площадь F1 , скорость движения C1, плотность газа в этом сечении r1 , давление р1. Сечение «1» расположено на высоте h1 относительно условного уровня. В сечении «2», расположенном на высоте h2, параметры соответственно равны C2, F2, r2, р2.
Через некоторый интервал времени Dt газ из сечения «1» переместится на расстояние Dl1=C1·Dt, а из сечения «2» на расстояние Dl2=C2·Dt. Согласно уравнению неразрывности через эти сечения за время Dt проходит одинаковая масса жидкости:
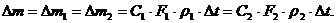(7)
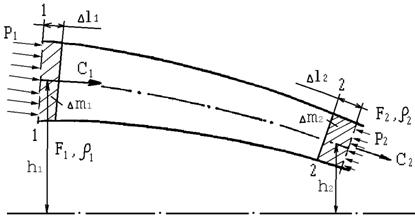
Рис.13. К выводу уравнения Бернулли
Как было сказано ранее (см. п.2.3), через стенки струйки не происходит переноса энергии. Но на выделенный объем, заключенный между сечениями «1» и «2», оказывают влияние силы, обусловленные давлением газа р1 и р2. С учетом этого можно сказать, что энергия газа в сечении «1» (Е1) будет отличаться от энергии в сечении «2» (Е2) на величину работы сил от давления газа. Работу этих сил можно определить по формулам:
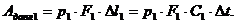(8)
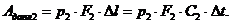(9)
С учетом сказанного можно записать:
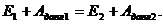(10)
Энергия газа для струйки тока будет складываться из кинетической энергии, обусловленной движением газа, и потенциальной энергии, обусловленной изменением положения массы газа относительно условного уровня., т. е.: Е = Екин. + Епот.*. Кинетическую и потенциальную энергии газа можно определить по формулам:
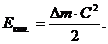(11)
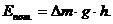(12)
Тогда с учетом (7) — (12) можно записать:
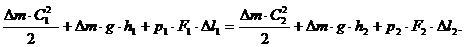(13)
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 |
