Теперь мы можем установить отношения между Q(aθ·cos-1 χ) и Q(m0). пусть m0 соответствует электронной плотности линии αm0. Используя уравнение 3 на странице (?) снова, мы находим

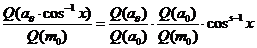
(11)

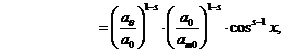(12)

где мы использовали α0, минимальную регистрируемую линейную электронную плотность в направлении максимальной чувствительности антенны. Это позволит нам позже привести ξсо к чувствительности радара введенный в раздели 3 на странице(?).

Теперь мы можем вычислить число потоковых метеоров множеств dN зарегистрированных в единицу времени в бесконечно малом секторе dθ:

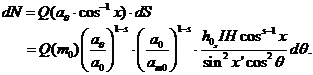
(13)

---

1.4 Приведение к минимальной регистрируемой линейной электронной плотности α0, и интегрирование по всем направлениям θ в плоскости эха.

Теперь следующий шаг - интегрирование уравнения 13 по углу θ в плоскости эха. Мы не можем однако выполнить эту операцию сразу же, поскольку чувствительность антенны изменяется как функция угла θ. В соответствии с направлением, минимальная регистрируемая линейная электронная плотность изменяется так же как и вероятность регистрирования недоуплотненных и переуплотненных метеорных следов.

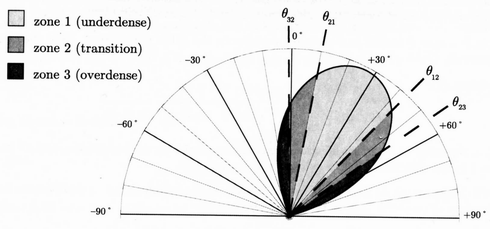
рисунок 2 - три метеорных зоны внутри диаграммы направленности антенны. Коэффициенты усиления антенны G = GT = GR заданны как функции угла θ.

Чтобы учесть это, мы делим плоскость эха на три зоны, как показано на рисунке 2. В первой зоне, минимальная регистрируемая линейная электронная плотность αθ соответствует недоуплотненным метеорным следам, то есть, αθ <αc (αc приведено в формуле 27 на странице(?)), и большинство наблюдаемых метеоров будут недоуплотненными. Вторая зона имеет αθ ≈ αc и относится к переходной области между недоуплотненными и переуплотненными следами. Третий соответствует переуплотненным метеорным следам, то есть, αθ > αc. Все метеорные следы, наблюдаемые в этой зоне, являются переуплотненными.

В каждой из этих зон, мы определим вариацию αθ как функцию θ, чтобы привести число наблюдаемого эха в данном направлении к нашей минимальной массе m0. Мы обработаем эти зоны отдельно, чтобы сосчитать их общее зарегистрированное число метеоров N1, N2 и N3, и затем сосчитаем общее количество зарегистрированных метеоров N = N1 + N2 + N3.

1.4.1 Предварительные вычисления

Вспомним уравнение 3 на странице (?) и уравнение 4 на странице (?):

где

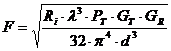
в направлении отражающей точки.

Рассмотрим две эквивалентные системы координат для определения направления на небесной сфере. Азимут φ (относительно направления максимального усиления антенны) и угол возвышения δ диаграмм направленности и . Однако, когда рассматриваем параметры относящиеся к данному метеорному потоку, то проще использовать зенитный угол радианта потока относительно зенита в точке радиолокатора и угол в плоскости эха θ. Переход от одной системы координат к другой показан в следующем уравнении:

где – это азимут направления максимума диаграмм направленности антенны радара, и азимут радианта.

F изменяется как функция углов и :

= F(δ,φ) =

где δ и φ угол возвышения и азимут отражающей точки, (δ,φ) и (δ,φ) усиления диаграммы направленности антенн передатчика и приемника относительно изотропного излучателя в свободном пространстве, C константа, соответствующая значению 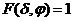в направлении максимума усиления антенны. Обычно для передатчика и приемника радиолокатора используется одна и та же антенна, т. е. ( δ,φ ) = (δ,φ ).

Теперь определим как

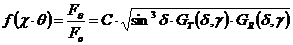
где это величина F в направлении максимально чувствительной антенны, и выбрано таким образом, что в направлении максимального чувствительного радара.

В конце концов, если U это пороговый уровень приемника радиолокатора, минимальная регистрируемая электронная линейная плотность в направлении максимальной чувствительности радара, то мы имеем:

,

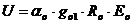где соответствует направлению максимальной чувствительности антенны. Это означает, что соответствует отражению от недоуплотненного следа в направлении максимальной чувствительности антенны.

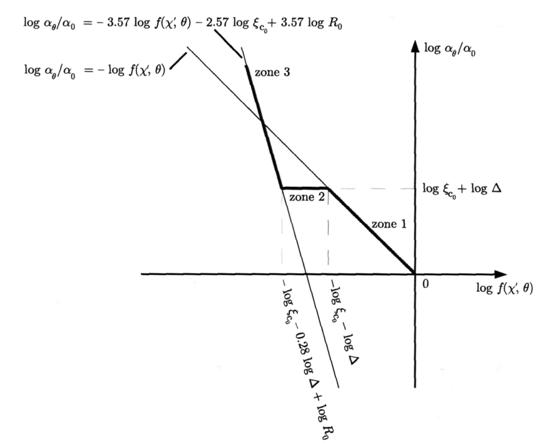
Рис. 3 Изменение , как функция от для трех метеорных зон, для . . Показывает геометрическую зависимость амплитуды метеорного эха относительно электрической плотности в бесконечно малом секторе . Всевозможные уравнения в графическом пояснении в тексте.

1.4.2 Зона 1

В первой зоне, минимальная регистрируемая электронная линейная плотность соответствует недоуплотненному метеорному следу. Используя уравнение 27 на странице 33, мы получаем запись:

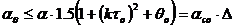
где ∆ определяется как . Делим его на , отсюда следует:

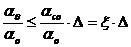
Рассматривая уравнение 19 и

Мы получаем:

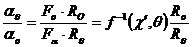
Это отношение справедлива для зоны 1, показано в фигуре 3.

Комбинация уравнения 21 и 23 дает нам последующую границу для зоны 1:

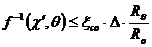
Эта граница зоны 1 так же показано в фигуре 3. Заметим что 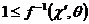всегда больше или равно .

Если мы заменим уравнение 23 в уравнении 13, мы получим

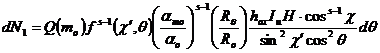
Мы сейчас проинтегрируем это выражение:

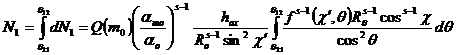
где и границы угла зоны 1 показано в фигуре 2. Они решении уравнения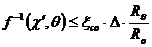

1.4.3 Зона 2

Рассудим почему мы имеем область перехода между переуплотненными и недоуплотненными метеорами, это то, что коэффициент отражения переуплотненных метеоров ниже чем тот же недоуплотненного метеора . Это приводит к ступеньке в фигуре 2.

Граничные условия для зоны 2, переходная зона между недоуплотненными и переуплотненными метеорами выводится из условии зоны 1 и 3, данный в уравнении 24 и 41:

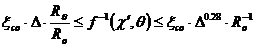
Для метеоров в этой зоне, мы имеем

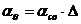
или разделим на

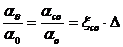
Если мы подставим это в уравнение 13, мы получим

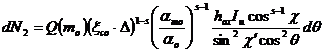
Мы сейчас интегрируем это выражение:

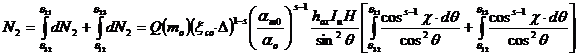
где 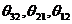и граница угла трансляции между зонами 1 и 2 так как в фигуре 2. и является решение уравнения , от сюда можем вывести фигуры 3. Соответствующие расчеты для этого условия дается в секции 1.4.4.

1.4.4. зона 3.

В зоне 3 регистрируются только переуплотненные метеоры. Из формулы 8 на странице мы имеем:

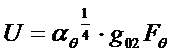. (32)

Объединяя с формулой 19, получим уравнение:

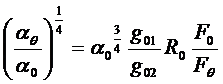. (33)

Так как в соответствии с формулой 20 на странице

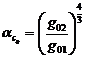, (34)

мы видим что

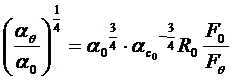, (35)

и, следовательно, мы делаем вывод что

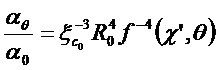. (36)

Принимая во внимание другие эффекты (т. е. то что переуплотненные метеоры имеют тенденцию испаряться на низких высотах, то расстояние между антенной и отражающей точкой также имеет тенденцию уменьшаться) мы находим несколько отличную эмпирическую формулу (Белькович 1971г.):

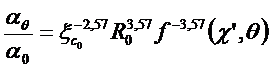. (37)

Это отношение показано на рисунке 3, представленной переуплотненными метеорами в зоне 3.

Если мы подставим его в уравнение 13, мы получим:

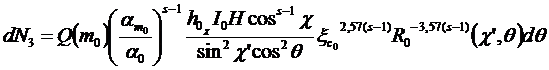(38)

Проинтегрируем это выражение:

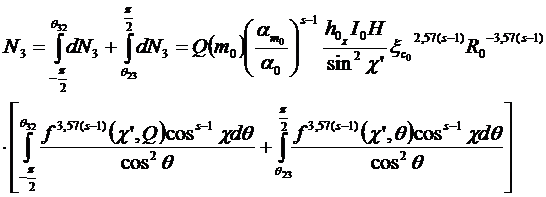(39)

где и граничные углы зоны 3. Они определяются из условия для зоны 3, которое выводится из рисунка 3:

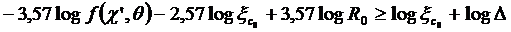. (40)

Это дает:

. (41)

1.4.5. Заключение

Число зарегистрированных потоковых метеоров . Если мы знаем из наблюдений (после того как исключили спорадический фон) мы можем сосчитать остальные параметры по формулам 26, 31 и 39 и, подсчитав их мы можем высчитать плотность потока метеоров с массой больше .

2 Определение плотности потока с использованием часового числа радиоэхо от переуплотненных метеорных следов

Выше мы рассмотрели определение плотности потока метеорных тел по всем зарегистрированным радиоэхо с амплитудой больше чем пороговый уровень приемника радиолокатора. Эти эхо в большинстве своем принадлежат к 1 зоне антенны, то есть соответствуют недоуплотненным метеорным следам.

Мы можем также попытаться найти плотность потока из числа радиоэхо, принадлежащим только переуплотненным метеорным следам. Для радиолокаторов с это эхо длительностью сек. Часовые числа таких эхо значительно меньше, чем числа всех зарегистрированных эхо, таким образом, мы теряем точность определения . Однако мы выигрываем, потому что число наблюдаемых метеоров меньше зависит от диаграммы направленности антенны, а также количество параметров, которые необходимо определять, значительно меньше.

Необходимо заметить, что прежде чем начать вычисления потока, спорадический фон метеорных эхо должен быть исключен, как это показано на странице ***.

Длительность Т радиоэха от переуплотненных метеорных следов определяется как (см. формулу 17 на стр. ):

(42)

где 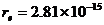м-1 - классический радиус электрона, время спада на высоте отражающей точки, и 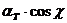линейная электронная плотность следа с зенитным углом радианта , - линейная электронная плотность следа того же метеороида, который вошел бы в атмосферу вертикально. и - величины и на высоте отражающей точки, а для - еще и в секторе под углом .

Допустим минимальная электронно-линейная плотность следа, которая может обеспечить длительность эха , при .

Мы получим:

, (43)

где , и время спада, начальный радиус и величина - высота точки отражения в этом случае. Ясно что для максимальной продолжительности, должно быть большим, что означает что отраженная точка расположена ниже в атмосфере. Вместо размера , мы можем взять типичную величину для нее, т. е. использовать видео наблюдение (см. рисунок 2 на стр. ).

Выбирая и объединяя выражения 42 и 43, мы получим:

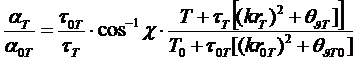. (44)

Поскольку и на 2 – 3 порядка меньше чем и , то ими можно пренебречь, тогда

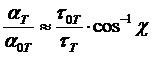, (45)

Или воспользовавшись выражением 2 на стр. :

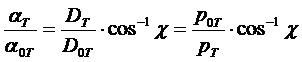, (46)

где и коэффициенты амбиполярной диффузии и и давление атмосферы на высоте и соответствующие и .

Воспользовавшись выражением (3) на стр.*** мы получим:

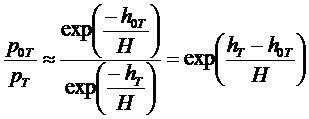. (47)

и являются максимумами электронно-линейной плотности, так что мы можем использовать формулы 15 и 16 на стр.*** . Т. к. мы рассматриваем переуплотненные метеоры, мы должны использовать формулу для . Опорный метеор (обозначим ) вертикальный, но другой () – нет. В результате мы получим:

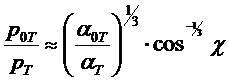. (48)

В результате из формул 46 и 48 мы имеем:

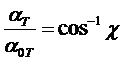(49)

Теперь мы можем вычислить плотность падающего потока метеороидов с длительностями эхас. для площадки dS, которая показана на рис.1.

Мы знаем, что наблюдаемое число метеоров с длительностью более 1с., пересекающих площадку dS, равно:

(50)

Где по аналогии с формулой (5), мы знаем что

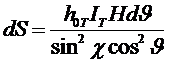. (51)

Таким образом, по аналогии с равенством (13) можно записать:

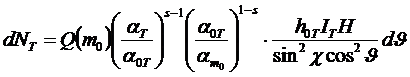. (52)

Использую формулу (49) и интегрируя ее по плоскости эха получим:

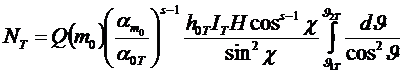, (53)

где (Белькович, 1988)

, (54)

это толщина метеорного слоя, соответствующего отражениям с длительностью не меньше с. Пределы интегрирования и должны быть найдены из условия что амплитуда эха выше порогового уровня, т. е. 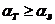или (см. формулу 37):

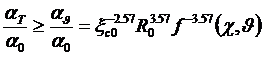. (55)

Отсюда следует вывод что углы и есть корни уравнения

. (56)

Необходимо отметить, что показанное выше приближение соответствует только зеркальным радиоэхо от переуплотненных метеорных следов. Незеркальные отражения, или рассеяние на следах после того как они будут искажаться ветром, не рассматриваются. Это не является проблемой для метеорных потоков со скоростями меньше 45-50 км/ч (таких как Геминиды и Квандратиды). В этих случаях высоты следов меньше 100 км и процесс прилипания свободных электронов к нейтральным молекулам атмосферы ограничивает длительность эха. Эхо исчезает до того момента, когда след мог бы быть значительно искривлен ветром. В Энгельгартовской астрономической обсерватории проводится работа, целью которой является обработка наблюдений потока Эта-Акварид. Уже есть неплохие готовые результаты, так что, похоже, и эта проблема будет решена.

Литература

(1971). Статистическая теория радиолокации метеоров. Из-во КГУ.

104 с.

(1988). Статистическая теория метеоров. Дисс. на соиск. Д. ф.-м. н.

302 с.

Обработка радиолокационных наблюдений 3:

Расчет плотности потока метеороидов и параметра s

Показано, как практически сделать расчет параметра s и плотностей потока метеороидов и по результатам радиолокационных наблюдений. Этот метод проиллюстрирован на результатах многолетних радиолокационных наблюдений метеорного потока Геминид.

1.  Алгоритм для расчета параметра s распределения метеорных тел по массам

Величина параметра s которая должна быть использована в формулах для подсчета плотности потока метеороидов, может быть найден разными методами, например из распределения амплитуд радиоэха (смотри рисунок 3 на стр. ), или из распределения длительностей радиоэха (Белькович 1971; Белькович 1988). В этом случае, формулы для распределения амплитуды и длительности эха были выведены и с учетом случайных положений отраженных точек на ионизированных следах метеора. Предыдущие подходы (Кайзер 1953) из формулы выводились в предположении, что точки отражения совпадают с точками максимальной ионизации.

Проблема при использование наблюдений простого радара в том, что мы не можем различать эхо потоковых метеоров от спорадического фона эх. Так вышеупомянутая техника страдает от спорадического загрязнения. Вот почему мы предположили другой путь определения величины s, который представлен на рисунке 1 и объяснен ниже.

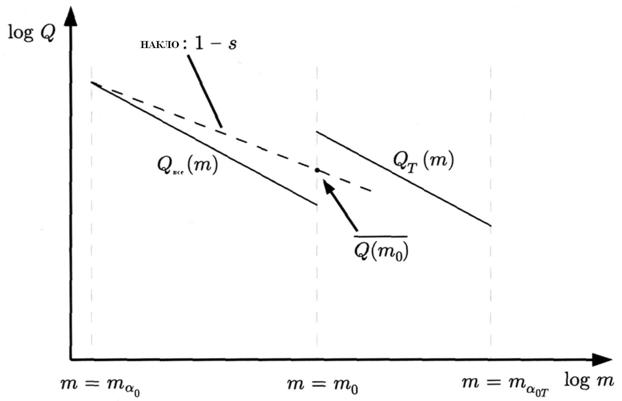
Рис. 1.- Итерационный метод для определение величины параметра s из 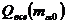и 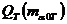. Оба значения плотности потока, были получены из подсчетов чисел метеорных, и таким образом очищенных от загрязнения спорадического фона. Принимая выбранный параметр s, обе плотности потока пересчитывается к массе . Среднее значения потока для массы дает улучшенную оценку параметра s, которая используется как исходная точка для нового приближения.

Обратим внимания, прежде чем примененить данный метода, мы должны исключить спорадический фон из наблюдаемых числового числа метеора, как для полного числа метеоров, так и для числа метеоров длительностью более 1 секунды.

Алгоритм состоит из следующего:

1.  Выберите начальную величину для s, например s=2.

2.  Вычислите (секция 1стр. ) и (секция 2 стр. )

3.  Приведите и к общей минимальной массе метеороида 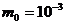г, используя уравнения 3 (страница ), для того чтобы получить 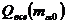и .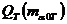

4.  Вычислите среднюю плотность потока для :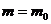

(1)

5. Вычислите коэффициент наклона s-1, как показано на рисунки 1:

(2)

6. Повторяйте процедуру с 2 шага до тех пор пока , где желаема точность.

2 Алгоритм для вычисления плотности потока потоковых метероидов Q.

Теперь мы должны описать вычисление потока плотностей и 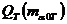на практике, т. е., как мы можем выполнить шаг 2 в раздели 1.

2.1. Шаг 1: Определение и для вертикального метеора.

Для того чтобы вычислить плотность потока двумя разными способами, нам нужно найти две высоты, величину соответствующую максимальной ионизации вертикального потокового метеора с электрона линейной плотности (так как мало, фактически является высотой), и высота соответствует максимальной ионизации для вертикального потокового метеора с .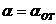

Характеристическая высота , к сожалению, зависит не только от массы метероида m и скорости , но так же и от объемной плотности p метероида. Последнее зависит от физической структуры родительского тела потока и обе высоты могут быть найдены из базисных видео наблюдений. Поэтому сложно использовать общую формулу для и . Так как обе величины должны быть найдены через многочисленную видео станцию наблюдения. Рисунок 2 показывает как высоты максимальной блеска потоковых метеоров должны быть нанесены против абсолютной звездной величины (т. е. звездная величина метеора появившийся из зенита на расстояние 100 км от наблюдателя), учитывая поправку на угол зенита при видео наблюдения (смотри уравнение 15 на странице ):

(3)

Используем эту формулу для преобразования метероидных высот, наблюдаемых на спутниках из действительного зенитного угла до .

Вспомним формулу 9 на странице 23:

[в ] (4)

где m (в кг) есть масса метеороида, (в км/с) - скорость, H (в км) приведенная высота атмосферы и максимальная электронная линейная плотность на метеорном следе. Эмпирическое отношение между массой метеороида и абсолютной звездной величины дано (Белькович 2001):

(5)

где m выражена в кг и км/с.

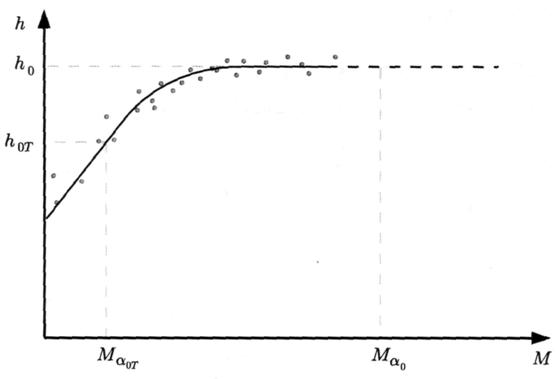
Рис. 2. Определение высот максимальной ионизации и с использования двойных станций, полученные при наблюдение телевизионной станции. Высота соответствует . Где М абсолютная звездная величина метеороидов.

Совместив уравнения 4 и 5, мы получаем:

Используя эту формулу мы сможем вычислить абсолютные звездные величины, и соответствующие и .

обычно соответствует , намного слабее, чем метеороиды наблюдаемые телевизионным способом. К счастью, высота максимального блеска равна на протяжение большого интервала звездной величины, и мы можем использовать наблюдаемого части плато.

Мы сначала выбираем начальную величину , надо выбрать начальную величину для , т. е., =95 км. Используя формулу 13 на стр. 24 и 2 на стр. 27, мы находим соответствующую величину для . Уравнение 43 на стр. 45 выдает нам соответствующую величину для . Мы можем использовать уравнение 6 чтобы вычислить соответствующую величину для . Теперь мы можем найти следующее приближение для , беря величины соответствующую на рис. 2. Мы повторяем эти шаги пока 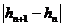относительно мало.

2.2. Шаг 2: исправляем для зенитного угла .

должно быть исправленным для зенитного угла метеорного потока и на момент наблюдения радара, соответствии с формулой 14 на стр. .

2.3. Шаг3: вычисление различных параметров на высоте и .

Ряд атмосферных параметров и серия соответствия параметров должны быть определены.

·  начальный радиус следа на высотах и используя уравнения 12 на стр. ,

·  коэффициент абиполярной диффузии на высотах и используется уравнение 13 на стр. ,

·  постоянное время на высотах и используется уравнение 2 на стр. ,

·  временное отношение на высотах и используется уравнение 6 на стр. ,

·  фактор коррекции амплитуды на высотах и используется уравнение 5 на стр. 29.

2.4. Шаг 4: вычисления потоков.

Рассчитаем плотность потока 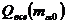и 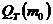путем интегрирования по углу в плоскости эха для соответствующие итерационной величины s, как объясняется в параграфе 1 на стр. и в параграфе 2 на стр. .

3. Форматы данных и программного обеспечения, использованные Энгельгардта в Астрономической Обсерватории в Казани.

В Казанской Астрономической Обсерватории имени Энгельгардта производилось наблюдения числа радио эха, накапливались в таблицу 1, данные накапливались в таблице 2 для одного часового интервала наблюдения.

TYPE MeteorN=RECORD

year : integer; год

AC : single;

AZI : byte;

mon : byte; месяц наблюдения

day : byte; дней наблюдения

Mth : byte ; местное время наблюдения

NA : integer;

NT : single;

end;

Таблица 1. Записи хранения данных использованные для запоминания часового эха.

TYPE MeteorF=RECORD

year : integer;

AC : single;

AZI : byte;

mon : byte;

day : byte;

Mth : byte;

NA : integer ;

NT : single;

cZ : single;

Az : single;

S1 : single; s-1

QA3: single;

QT3: single;

LSS: single; (J2000.0)

end:

Таблица 2. запись хранения данных используется для накопления результатов обработки.

Две программы используются для анализа этих записей. Первая усредняет s, как функция долготы солнца . Величины s в выходных файлах приводиться в месте с ошибками. Эти ошибки приводят к дополнительным ошибкам в определение плотности потока метеороидов Q. Чтобы избежать этого, функция S() должна быть сглажена усреднением среднего числа.

Вторая программа необходима для перерасчета профайла Q() с использованием сглаживания S(). Мы должны подчеркнуть, что эта программа должна использовать фиксированные величины S, для повышение точность величины Q.

4. Пример результатов наблюдения.

Вычисление усреднения параметра s показано на рис.3 и рис.4. В последнем только точки с > 0.84 были выбраны, для того чтобы обеспечить меньший разброс результатов.

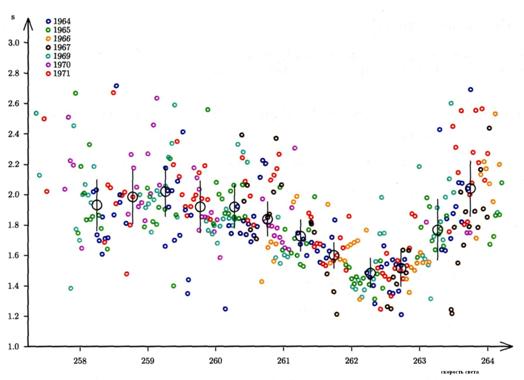
Рисунок 3 – Первичные (малые кружки) и усредненные (большие кружки) параметр s Geminids как функция долготы солнца (J2000,0) для нескольких лет.

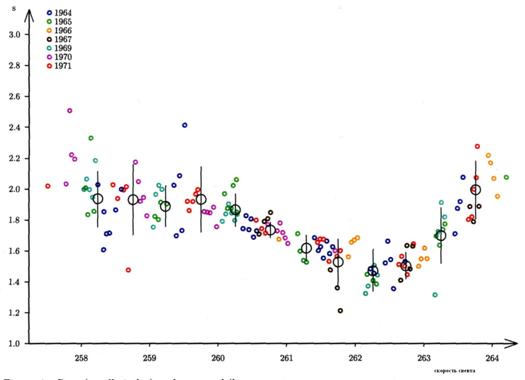
Рисунок 4 - Первичные (малые кружки) и усредненные (большие кружки) параметр s Geminids как функция долготы солнца (J2000,0) для нескольких лет. Были взяты только точки, когда > 0.84 (X <33) были взяты в расчет, что привлекло значительное уменьшение рассеивания данных.

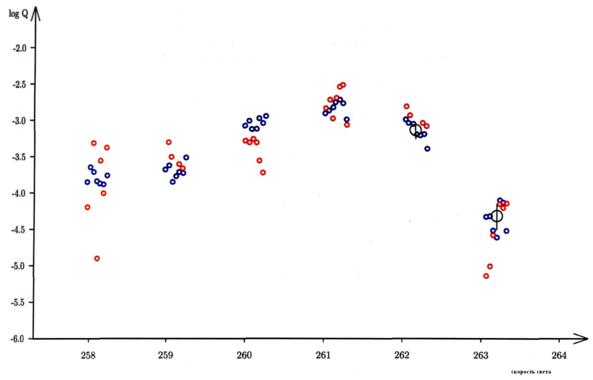
Рис. 5. Профиль логарифма потока плотности Geminids в 1971, как функция долготы солнца (J2000,0). Голубые круги показывают величину , красные круги показывают .

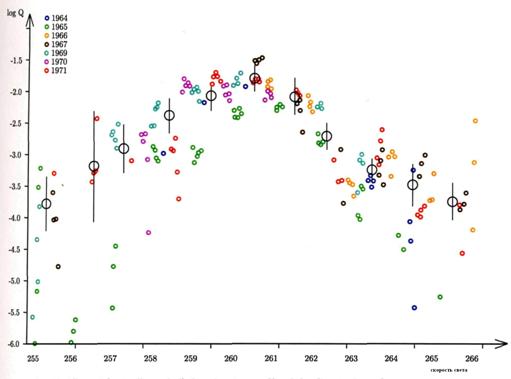
Рис. 6. (Логарифмическая шкала) профиль потока плотности Geminids в период , как функция скорости солнечного света (J2000,0). в связи с тем что потоки Geminids стабильны, активность очень похожа из года в год.

Рисунок 5 показывает профиль плотности потока (голубые круги на графе; все эхо) и ( красные круги на графе; полученные по эха, продолжительностью 1 или более секунд) для Geminids 1971г. нет значительной разнице между двумя потоками, вычислены различными методами, основанными на различныех физические аспекты отраженные радио волн.

Результаты, полученные программы усреднения величин Q (за несколько лет наблюдений), показаны на рисунки 6. Программа дает возможность выбрать для анализа различные результаты долготы солнца, интерационное усреднение, годы наблюдения и минимального значения . На выходе результаты представляют не только в форме графиков, но также как в виде числовой таблице.

Ссылки:

(1971) Статистическая теория наблюдения метеороидного радара. Казанский университет, Россия,104 стр. На Русском.

(1988) Статистическая теория метеороидов. Казанский Университет, Россия, 301 стр., На Русском.

, , и «Сравнительный анализ потоков метеоройдных наблюдений, произведенный тремя разными методами». В ESA SP-495: Метеороидная конференция 2001, 91-93 стр.

(1953) «Изучения радио эха метеороидной ионизации»

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4