где ![]() - коэффициент отражения для переуплотненных следов:
- коэффициент отражения для переуплотненных следов:
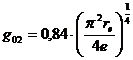
![]() . (9)
. (9)
Коэффициент 0.84 обусловлен рефракцией радиоволн в недоуплотненных внешних областях следа (Маннинг, 1953).
В случае отражения радиоволн от переуплотненных метеорных следов нет никакой необходимости учитывать поправочный коэффициент ![]() .
.
Критический радиус ионизированного следа метеора в (м) в момент времени t (с) после формирования метеорного следа в данной точке, задается как:
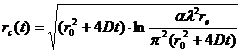 , (10 )
, (10 )
где ![]() (м
(м![]() /с) - амбиполярный коэффициент диффузии,
/с) - амбиполярный коэффициент диффузии, ![]() (м) – начальный радиус следа,
(м) – начальный радиус следа, ![]() (м
(м![]() ) – линейная электронная плотность метеорного следа,
) – линейная электронная плотность метеорного следа, ![]() (м) – длина волны радиолокатора, и
(м) – длина волны радиолокатора, и ![]() (м) –классический радиус электрона. Критический радиус достигает максимального значения
(м) –классический радиус электрона. Критический радиус достигает максимального значения ![]() во время
во время ![]() , где
, где
![]() (11)
(11)
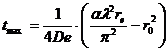 . (12)
. (12)
Приведенная к входу приемника амплитуда сигнала ![]() (в), для эха от переуплотненного метеорного следа в момент времени
(в), для эха от переуплотненного метеорного следа в момент времени 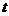 после его формирования задается уравнением:
после его формирования задается уравнением:
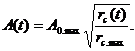 (13)
(13)
Отражение от переуплотненного метеорного следа заканчивается, когда критический радиус исчезает. Теперь мы можем найти длительность сигнала от переуплотненного следа ![]() (с), подставив в формуле (10) . Необходимо заметить, что за счет времени прохождения
(с), подставив в формуле (10) . Необходимо заметить, что за счет времени прохождения ![]() метеорного тела через половину первой зоны Френеля и периода повторения импульсов радара
метеорного тела через половину первой зоны Френеля и периода повторения импульсов радара ![]() , длительность T переуплотненного метеора всегда недооценивается в среднем на величину
, длительность T переуплотненного метеора всегда недооценивается в среднем на величину ![]() . Чтобы найти истинное наблюдаемое время T, мы должны учитывать:
. Чтобы найти истинное наблюдаемое время T, мы должны учитывать:
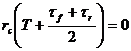 (14)
(14)
С учетом уравнения (10), это означает
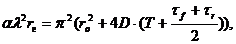 (15)
(15)
или, используя уравнения (2) и (6):
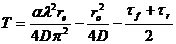 (16)
(16)
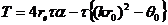 (17)
(17)
Нужно заметить, что второй член мал по сравнению с первым.
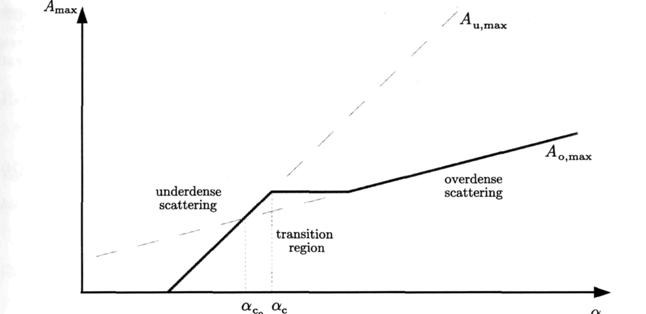
Рис. 4 Логарифм максимальной амплитуды метеорного эха ![]() , как функция логарифма линейной электронной плотности
, как функция логарифма линейной электронной плотности ![]() .
.
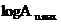 - логарифм амплитуды отраженного сигнала от недоуплотненного следа возрастает так же быстро, как и функция log α. Для переуплотненного эха крутизна возрастания. меньше. Нужно заметить, что для α>αc0, амплитуда эха для недоуплотненного следа должна бы быть больше чем амплитуда эха от переуплотненного метеорного следа. Однако, за счет начального радиуса и диффузии за время формирования следа между переуплотненными и недоуплотненными зонами существует область, где не применимы формулы для обоих типов следов – так называемая переходная область. Для нашей физической модели мы будем считать, что в этой области коэффициент отражения не меняется.
- логарифм амплитуды отраженного сигнала от недоуплотненного следа возрастает так же быстро, как и функция log α. Для переуплотненного эха крутизна возрастания. меньше. Нужно заметить, что для α>αc0, амплитуда эха для недоуплотненного следа должна бы быть больше чем амплитуда эха от переуплотненного метеорного следа. Однако, за счет начального радиуса и диффузии за время формирования следа между переуплотненными и недоуплотненными зонами существует область, где не применимы формулы для обоих типов следов – так называемая переходная область. Для нашей физической модели мы будем считать, что в этой области коэффициент отражения не меняется.
Переходная линейная электронная плотность.
Теперь рассмотрим переходную область между недоуплотненным
и переуплотненным радио эха. Первое приближение мы выбираем как
критерий перехода, что Au, max=Aо, maх и выбираем R = 1. Это
идеальный случай, т. к мы не учитываем начальный радиус, диффузию и
эффект конечного времени между двумя импульсами (Белькович, 1971).
![]() (18)
(18)
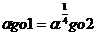 (19)
(19)
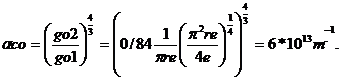 (20)
(20)
Эта оценка однако, слишком приблизительна. Поэтому мы получим
более точное уравнение для переходной линейной электронной плотности
между недоуплотненным и переуплотненным отражениями,
основанными на физике плазмы.
Мы знаем из уравнения 11 на странице 23, что
электронная объемная плотность в метеорном следе изменяется во
времени t после формирования, и на расстоянии r от оси следа:
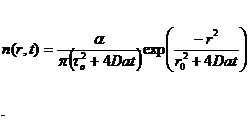 (21)
(21)
Из физики плазмы мы знаем, что диэлектрическая постоянная в плазме,
![]() , (22)
, (22)
где k = ![]()
![]() .
.
Согласно (Кайзер, 1953), для узкого следа с большой отрицательной
диэлектрической постоянной к на оси, условие проникновения
падающей волны для недоуплотненного отражения:
![]()
(23)
Рассмотрим след метеора в момент времени t = (![]() )/2
)/2
после его формирования. Электронная объемная плотность на
оси следа метеора (r = 0) тогда:
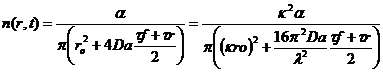 (24)
(24)
Используя уравнения 2 и 6, что приводит к выражению:
n(0,t)=![]() (25)
(25)
Отражение от метеора будет недоуплотненное, если падающая волна
может проникнуть через след полностью к оси следа с момента
формирования следа t = 0 .Из уравнений 22, 23, и 25, мы получаем:
![]() , (26)
, (26)
или
![]() , (27)
, (27)
Физическое значение aCn и ac можно рассмотреть на рисунке 4. Как
показывалось ранее, ![]() изменяется вдоль следа метеора, то есть,
изменяется вдоль следа метеора, то есть,
![]() (28)
(28)
так что один и тот же след метеора может быть зарегистрирован как
недоуплотненным или переуплотненный, в зависимости от положения
точки отражения (см. рисунок 5).
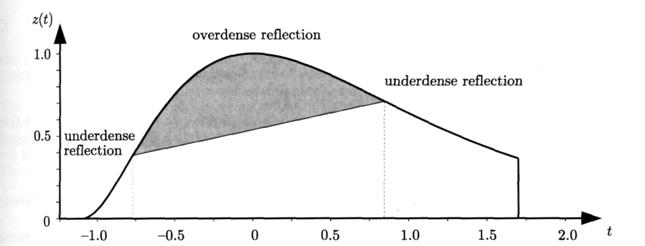
Рисунок 5 - Некоторые части следа метеора будут вести себя как
недоуплотненные следы, в то время как в районе максимума ионизации
отражения могут быть как и от переуплотненных. За счет влияния
начального радиуса и диффузии, границы будут большими
на больших высотах, более высокая электронная плотность
необходима для больших высот, чтобы отражения
были переуплотненными.
Литература
Белькович 0. И. (1971). Статистическая теория радиолокации метеоров.
Казанский Университет, Россия, 104 страницы.
Kaiser T. R. (1953). "Radio echo studies of meteoric ionization". Adv. Физика,
2, 495.
Manning L. A. (1953). "The strength of meteoric echoes from dense columns
". J. Atm. Terr. Физика, 4, 219-225.
Обработка радиолокационных наблюдений 2:
Спорадический фон, уровень регистрации, чувствительность радиолокационной станции
Метод нужен для того, чтобы определить и исключить спорадический фон из результатов радиолокационных наблюдений, направленных на изучение активности метеорного потока. Объясняется, как правильно установить верхний порог для регистрации метеоров. И, наконец, здесь рассматриваются два метода для определения чувствительности радарного оборудования.
1. Определение и исключение спорадического фона
Во время радиолокационных наблюдений метеоров невозможно отличить, принадлежит ли данный метеор спорадическому фону или какому–то определенному метеорному потоку.
Сложные радиолокационные системы с несколькими разнесенными приемными антеннами, конечно, могут быть использованы, но они слишком сложны и дороги в эксплуатации. Кроме всего прочего, такие сложные системы теряют приблизительно ![]() всех зарегистрированных метеоров, потому что не все требуемые параметры могут быть зарегистрированы для каждого метеора в таких системах.
всех зарегистрированных метеоров, потому что не все требуемые параметры могут быть зарегистрированы для каждого метеора в таких системах.
Если мы хотим определить плотность потока метеорных тел ![]() , для этого мы должны знать часовое число метеоров, принадлежащих данному «потоку», а не число «потоков метеоров
, для этого мы должны знать часовое число метеоров, принадлежащих данному «потоку», а не число «потоков метеоров ![]() спорадических метеоров».
спорадических метеоров».
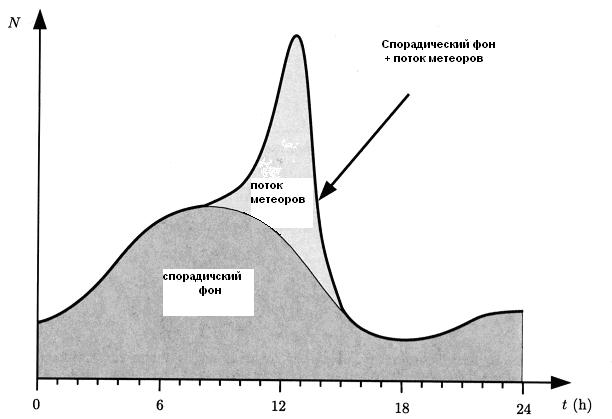
Рисунок 1. Наблюдаемый спорадический фон и поток метеорной активности изменяются в течение суток. Полное число ![]() наблюдаемых метеоров как сумма обоих.
наблюдаемых метеоров как сумма обоих.
Решая эту проблему, предположим, что спорадический фон не меняется сильно в течение нескольких последующих дней, но меняется медленно в течение года. Таким образом, мы можем сделать следующее:
1. Выполнить наблюдения за несколько дней до и после активности метеорного потока, когда регистрируется только спорадический фон.
2. Вычислить среднее часовое число метеоров спорадического фона для каждого часа суток до и после потоков.
3. Сделать то же самое для каждого дня наблюдений, когда действует метеорный поток, используя для этих целей линейную интерполяцию для каждого часа дня.
4. Для каждого часа дня активности метеорного потока вычесть часовые числа спорадического фона из наблюдаемых часовых чисел. В результате получим часовые числа потока.
Эти поправки необходимо сделать прежде, чем использовать наблюдательные данные для дальнейшей обработки методом, описание которого будет дано в дальнейшем.
2. Порог регистрации метеоров
Наша основная задача - определение плотности потока для потоковых метеоров ![]() , т. е. число метеороидов с массой
, т. е. число метеороидов с массой ![]() больше чем
больше чем ![]() .
.
Это определение напрямую основано на счете радиоэха. Для того чтобы избежать наблюдательной погрешности, надо с особой тщательностью выбрать порог системы, относящийся к приемнику, так, чтобы чувствительность системы была постоянной.
Наблюдаемая мощность ![]() приемника вычисляется по формуле:
приемника вычисляется по формуле:
![]()
![]()
где ![]() - мощность на входе приемника сигнала, отраженного от метеорного следа;
- мощность на входе приемника сигнала, отраженного от метеорного следа; ![]() - мощность излучения Млечного пути и других астрономических радио источников (включая Солнце, Луну и планеты), которые имеют суточные изменения. На частотах, типично используемых для наблюдения метеоров шум приемника намного ниже шума Млечного Пути
- мощность излучения Млечного пути и других астрономических радио источников (включая Солнце, Луну и планеты), которые имеют суточные изменения. На частотах, типично используемых для наблюдения метеоров шум приемника намного ниже шума Млечного Пути ![]() . Конечно, искусственный шум, такой как производимый электронными приборами или гармоники радиопередатчиков также могут быть источником шума. Наличие таких искусственных источников может создать трудности для установки соответствующего порогового уровня.
. Конечно, искусственный шум, такой как производимый электронными приборами или гармоники радиопередатчиков также могут быть источником шума. Наличие таких искусственных источников может создать трудности для установки соответствующего порогового уровня.
Мы измеряем ![]() , но для нас представляет интерес надежный счет метеоров с мощностью
, но для нас представляет интерес надежный счет метеоров с мощностью ![]() больше чем некоторый пороговый уровень
больше чем некоторый пороговый уровень![]() .
.
Если мы выбираем ![]() такой, чтобы он был в несколько раз выше
такой, чтобы он был в несколько раз выше![]() , то для всех метеоров с мощностью
, то для всех метеоров с мощностью ![]() , мы имеем:
, мы имеем:
![]()
![]()
Это означает, что если мы выбираем достаточно высокий порог, то для нас становятся безразличными суточные вариации ![]() , и мы можем использовать фиксированный порог регистрации. Мы будем пропускать более слабые метеоры, но мы выигрываем в том, что получаем надежный счет метеоров с
, и мы можем использовать фиксированный порог регистрации. Мы будем пропускать более слабые метеоры, но мы выигрываем в том, что получаем надежный счет метеоров с ![]() . Это проиллюстрировано на рисунке 2.
. Это проиллюстрировано на рисунке 2.
С цифровыми регистрируемыми системами и калиброванным приемником, мы можем вычислить ![]() из наблюдаемых
из наблюдаемых ![]() и
и ![]()
![]() , и соответственно решить, является ли сигнал
, и соответственно решить, является ли сигнал ![]() более сильным, чем сигнал
более сильным, чем сигнал ![]() . Но это показывает, что мы можем использовать более низкий порог
. Но это показывает, что мы можем использовать более низкий порог ![]() и несколько более точный порог регистрации.
и несколько более точный порог регистрации.
Если порог регистрации установлен (причем в виде напряжения на входе приемника; порог ![]() (в
(в ![]() ) представлен формулой:
) представлен формулой:
![]()
![]()
где ![]() (в
(в ![]() ) – входное сопротивление приемника. Для большинства коммерческих приемников это сопротивление равно
) – входное сопротивление приемника. Для большинства коммерческих приемников это сопротивление равно ![]()
![]() . Необходимо заметить, что уравнение (3) рассматривает мгновенную амплитуду и мощность на входе приемника. Часто рассматривается rms (среднеквадратичные значения) амплитуды и мощности. В этом случае уравнение читается следующим образом:
. Необходимо заметить, что уравнение (3) рассматривает мгновенную амплитуду и мощность на входе приемника. Часто рассматривается rms (среднеквадратичные значения) амплитуды и мощности. В этом случае уравнение читается следующим образом:
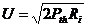
![]()
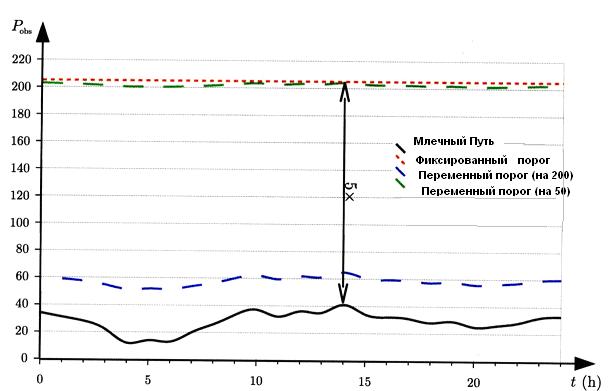
Рисунок 2. Два надежных способа для установления порога регистрации: вы
брать его значительно выше (здесь ![]() раз) чем максимальная мощность излучения с Млечного пути (из галактики) (фиксированный порог), или вычислить его, основываясь на текущей (в данный момент) мощности Млечного пути (переменный порог). Переменный порог, установленный (на
раз) чем максимальная мощность излучения с Млечного пути (из галактики) (фиксированный порог), или вычислить его, основываясь на текущей (в данный момент) мощности Млечного пути (переменный порог). Переменный порог, установленный (на ![]() ) показывает надежность выбора фиксированного порога.
) показывает надежность выбора фиксированного порога.
Этот способ выбран для подсчета второго множителя в формулах, относящихся к полученным метеорной амплитуде и мощности. В течение лекции мы систематически используем первое уравнение. Заметьте, что многие наблюдатели имеют свой порог регистрации, изменяющийся динамически с шумом, и, например, выбирают порог в 5![]() , где
, где ![]() - rms шума. Хотя это и позволяет определить эхо метеора, который нужен на данный момент, при этом отсутствует контроль над эффективной чувствительностью приема и полученные подсчеты для метеора теряют свой смысл.
- rms шума. Хотя это и позволяет определить эхо метеора, который нужен на данный момент, при этом отсутствует контроль над эффективной чувствительностью приема и полученные подсчеты для метеора теряют свой смысл.
Чувствительность радиолокационной станции
Мы выбираем в качестве меры чувствительности РЛС следующую величину:
![]()
![]()
где ![]() - минимальная регистрируемая электронная линейная плотность метеорного следа в направлении максимума чувствительности лепестка радиолокационной антенны. Относительная const
- минимальная регистрируемая электронная линейная плотность метеорного следа в направлении максимума чувствительности лепестка радиолокационной антенны. Относительная const ![]() приблизительно равна переходу между недоуплотненными и переуплотненными следами.
приблизительно равна переходу между недоуплотненными и переуплотненными следами.
Величина ![]() (
(![]() ) может быть найдена двумя способами. Первый метод основан на теории, использующей следующую формулу (Белькович,
) может быть найдена двумя способами. Первый метод основан на теории, использующей следующую формулу (Белькович, ![]() ):
):
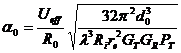
![]()
где ![]() (в
(в ![]() ) - расстояние от антенны РЛС до характеристической высоты
) - расстояние от антенны РЛС до характеристической высоты ![]() в направлении максимальной чувствительности антенны,
в направлении максимальной чувствительности антенны, ![]() и
и ![]() - это усиление передающей и принимающей антенн в этом направлении (линейное, относительно изотропного излучателя в свободном пространстве или в космосе),
- это усиление передающей и принимающей антенн в этом направлении (линейное, относительно изотропного излучателя в свободном пространстве или в космосе), ![]() (в
(в ![]() ) - длина волны радиолокатора,
) - длина волны радиолокатора, ![]() (в
(в ![]() ) - мощность передатчика, и
) - мощность передатчика, и ![]() (в
(в ![]() ) - входное сопротивление приемника. Фактор
) - входное сопротивление приемника. Фактор ![]() – есть значение
– есть значение ![]() в направлении максимальной чувствительности антенны.
в направлении максимальной чувствительности антенны. ![]() была введена в формуле (
была введена в формуле (![]() ) предыдущего раздела.
) предыдущего раздела.
![]() (в
(в ![]() ) – эффективный уровень порога радиолокационного приемника. Он отличается от порога
) – эффективный уровень порога радиолокационного приемника. Он отличается от порога ![]() определенного в уравнении
определенного в уравнении ![]()
![]() , за счет таких различных эффектов, как коэффициент потери в антенном фидере, который очень трудно определить.
, за счет таких различных эффектов, как коэффициент потери в антенном фидере, который очень трудно определить.
Столкнувшись с трудностью определения адекватных значений для ![]() , введем второй (более предпочтительный) метод оценки чувствительности РЛС, базирующийся на анализе наблюдаемого распространения амплитуд в двойном логарифмическом масштабе.
, введем второй (более предпочтительный) метод оценки чувствительности РЛС, базирующийся на анализе наблюдаемого распространения амплитуд в двойном логарифмическом масштабе.
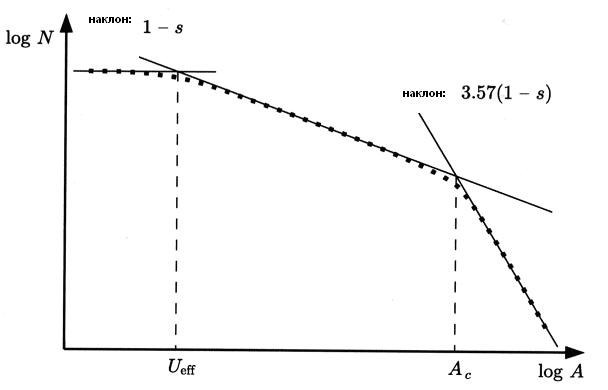
Рисунок 3. Интегральное распределение амплитуд радиоэха РЛС. Самая правая линейная часть соответствует переуплотненным радиоотражениям, тогда как эхо от недоуплотненных следов соответствует другой части графика, слева от ![]() . Слева от
. Слева от ![]() - предел чувствительности, график горизонтальный.
- предел чувствительности, график горизонтальный.
Интегральное распределение амплитуд метеорных радиоэха в двойном логарифмическом масштабе показано на рис.3. Минимальная регистрируемая электронная плотность ![]() может быть найдена из распределения амплитуд с помощью формулы (Белькович,
может быть найдена из распределения амплитуд с помощью формулы (Белькович, ![]() ; и Белькович,
; и Белькович, ![]() ):
):
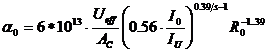
![]()
где ![]() – параметр распределения метеорных тел по массам;
– параметр распределения метеорных тел по массам; ![]() и
и ![]() - средние толщины метеорных слоев для недоуплотненных и переуплотненных следов соответственно. Безразмерные высоты
- средние толщины метеорных слоев для недоуплотненных и переуплотненных следов соответственно. Безразмерные высоты ![]() и
и ![]() вычисляются по следующим формулам (Белькович,
вычисляются по следующим формулам (Белькович, ![]() ; и Сулейманова,
; и Сулейманова, ![]() ):
):
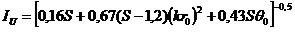
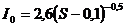
![]()
где ![]() - начальный радиус (в
- начальный радиус (в ![]() ),
), 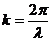 и угол
и угол ![]() был введен уравнением
был введен уравнением ![]() предыдущей главы. Величина
предыдущей главы. Величина ![]() может быть найдена из наклона левой ветви распределения амплитуд: наклон равен
может быть найдена из наклона левой ветви распределения амплитуд: наклон равен ![]() .
.
Эта формула была выведена для спорадических метеоров, значит только для спорадических метеорных радиоэхо. Следовательно, наблюдения для определения ![]() необходимо проводить в интервал времени, когда метеорный поток не наблюдаем.
необходимо проводить в интервал времени, когда метеорный поток не наблюдаем.
Литература:
Belkovich Suleymanova (1999)
(1971). Статистическая теория радиолокации метеоров Издательство КГУ, Казань, 104 с.
(1988). Статистическая теория метеоров. Диссертация доктора физико-математических наук, Казань, 301 с.
Обработка радиолокационных наблюдений 2:
Определение плотности потока метеорных тел
Даны два метода для определения плотности потока метеорных тел Q (m0) в метеорном потоке. В первом методе, рассматриваются все наблюдаемые метеоры, и решается задача путем вычисления величины собирающей поверхности в элементарном секторе в плоскости, приводя плотность потока в этом секторе к массе![]() , и интегрирование по всем направлениям плоскости эха. Второй метод использует число наблюдаемых переуплотненных метеоров с длительностью эха больше чем 1 секунда.
, и интегрирование по всем направлениям плоскости эха. Второй метод использует число наблюдаемых переуплотненных метеоров с длительностью эха больше чем 1 секунда.
1 Определение плотности потока, с использованием всех наблюдаемых метеоров
1.1 Геометрия и подход к решению задачи
В этом разделе, мы хотим получить плотность потока метеорных тел ![]() наблюдаемого метеорного потока. Для того, что бы это сделать, мы сначала должны вычислить число зарегистрированных метеоров в единицу времени (то есть часовое число), то есть то, что мы ожидаем при данных условиях для данного потока, соответствующего плотности потока метеороидов
наблюдаемого метеорного потока. Для того, что бы это сделать, мы сначала должны вычислить число зарегистрированных метеоров в единицу времени (то есть часовое число), то есть то, что мы ожидаем при данных условиях для данного потока, соответствующего плотности потока метеороидов ![]() .
.
Все ионизированные следы метеоров данного метеорного потока параллельны. Следовательно, благодаря свойству зеркального отражения на метеорных следах, все отражающие точки метеоров от этого потока будут лежать в плоскости эха, нормальной к вектору скорости метеорных тел (или направлению на радиант) и проходящей через точку, где находится радар, как показано на рисунке 1. Конечно, отражающие точки метеора должны также располагаться в метеорном слое в атмосфере.
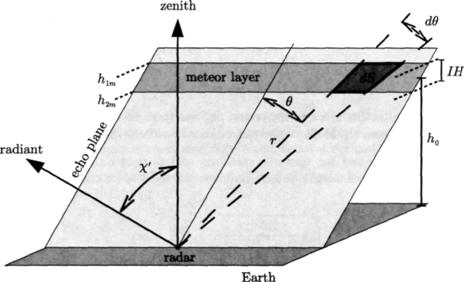
Рисунок 1 - Геометрия, используемая для текущих вычислений. Рисунок показывает положения радара, направление зенит, направление радианта потока, плоскость эха (перпендикуляр к направлению на радиант), зенитный угол ![]() относительно зенита в точке радара, метеорный слой которого пересекает плоскость эха, характеристическую высоту
относительно зенита в точке радара, метеорный слой которого пересекает плоскость эха, характеристическую высоту ![]() метеорного слоя, толщина метеорного слоя I H, и r, θ, И dθ определяющую площадку области dS в плоскости эха.
метеорного слоя, толщина метеорного слоя I H, и r, θ, И dθ определяющую площадку области dS в плоскости эха.
Мы начнем, рассматривать область пересечения бесконечно малого сектора в плоскости эха (заданной dθ на рисунке 1), и метеорного слоя в атмосфере: площадку dS. Мы начнем вычисление площади этой области, вычислим число dN метеоров потока зарегистрированных в единицу времени в этой площадке в случае плотности потока метеорных тел ![]() , и добавим число метеоров для всех этих секторов (это означает, что мы будем интегрировать по всем углам θ), для того чтобы в конечном итоге получить полное число N зарегистрированных метеорных потоков соответствующие
, и добавим число метеоров для всех этих секторов (это означает, что мы будем интегрировать по всем углам θ), для того чтобы в конечном итоге получить полное число N зарегистрированных метеорных потоков соответствующие ![]() .
.
1.2 Поверхность области dS в направлении
Первый шаг этого вычисления площади собирающей площадки dS изображенной на рисунке 1. Мы знаем что
(1)
является бесконечно малой областью, определяемой величинами r, dr, и ![]() .
.
-
Так как
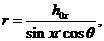 (2)
(2)
где h0x - характеристическая высота для наблюдаемого потока, исправленная для зенитного угла χ в отношении к зениту в точке отражения, как введено в разделе 3 на странице (?), и
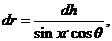 (3)
(3)
Мы можем написать:
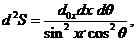 (4)
(4)
Мы теперь должны интегрировать по dh по всему метеорному слою, для того чтобы получить площадь dS в области описанной сектором dθ во всем метеорном слое:
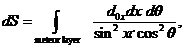 (5)
(5)
Метеорный слой, рассматриваемый в этом уравнении, однако, зависит от массы метеороида. Поэтому будем рассматривать только потоковые метеоры с массами между m и m + dm. Все потоковые метеоры с одной и той же массой (так же имеющие равные углы зенита χ', скорость v, и плотность ρ) будут иметь ту же самую максимальную ионизацию с линейной электронной плотностью αmax при высоте hmax, и при той же самой начальной высоте h1m = h0 + Ht1m и конечной h2m = h0 + Ht2m.
Для этой массы m, мы, таким образом, получаем значение dS:
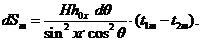 (6)
(6)
Если мы хотим вычислить среднюю величину dS для всех масс между m0 и ![]() , мы должны вычислить
, мы должны вычислить
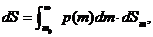 (7)
(7)
Где p(m) было приведено в уравнении 2 на странице (?). Отсюда:
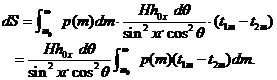
(8)
Теперь мы можем определить интеграл в этом уравнении как среднюю толщину метеорного слоя I. t1m - t2m вертикальная длина метеорного следа с массой m, что означает, что I – средняя вертикальная длина метеоров с массами, большими, чем m0. Выбирая m0 и обеспечивая наблюдения соответствующего начала метеора и высоты конца, мы можем вычислить I опытным путем. Это приводит к уравнениям 8 на странице (?) для Io и Iu, и уравнение 54 для IT
1.3 Число dN зарегистрированных потоковых метеоров в секторе dθ
При радиолокационных наблюдениях, направление на радиант перпендикулярно площадке dS. Число потоковых метеоров зарегистрированных в бесконечно малом секторе dθ есть площадка dS, умноженная на плотность потока, соответствующая метеорам, с минимальной регистрируемой линейной электронной плотностью αθ в их точке отражения, в направление θ.
Для потокового метеора с массой m, мы можем найти линейную электронную плотность α, соответствующую максимальной линейной электронной плотности αmax ионизированного следа, созданного этим метеорным телом, когда оно входит в атмосферу вертикально. Мы знаем что Q (α) = Q (m). Так как метеорный поток входит в атмосферу под углом χ к зениту выше отражающей точки, потоковый метеороид с такой же массой m производит максимальную линейную электронную плотность α∙cos χ
Теперь рассмотрим потоковый метеороид с минимальной регистрируемой линейной электронной плотностью αθ в его точке отражения. Этот метеор имел бы линейную электронную плотность aθ∙cos-1χ в его отражающей точке, если бы он вошел в атмосферу вертикально. Следовательно, Q(aθ·cos-1χ) плотность потока, соответствующая метеорным телам, которые создают линейную электронную плотность αθ в точке отражения в направлении θ и следовательно,
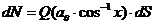 (9)
(9)
Из уравнения 3 на странице (?), мы выводим
![]()
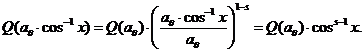 (10)
(10)

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 |



