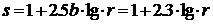 , (4)
, (4)
где b=0.92 (Кошак и Рендетель,1990а; Кошак и Рендетель,1990b)
![]()
![]()
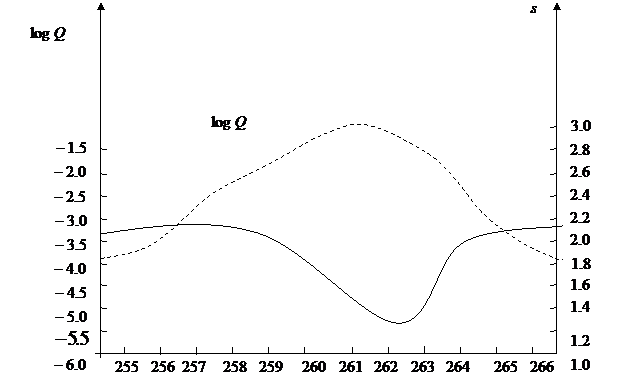

Рис.3. Профиль типичного метеорного потока. Q(m) и s как функции долготы Солнца λ. Разница между максимумом Q и минимумом s зависит от возраста метеорного потока.

![]()
![]()
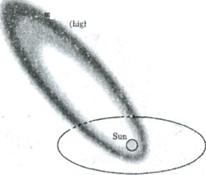
Рис.4. Пересечение орбитой Земли метеорного потока с большим наклонением орбиты к плоскости эклиптики (слева) и малым наклонением (справа).
Рис.4. Если наклонение орбиты метеорного потока велико (на рисунке слева), то Земля пересекает плоскость потока под большим углом и мы можем наблюдать метеороиды с орбитами приблизительно одного размера. Если же наклон мал (на рисунке справа), Земля пересекает поток таким образом, что имеется возможность наблюдения как внутренних, так и внешних его орбит и, следовательно, возможность оценить возраст потока на основе анализа распределений метеорных тел по массам как функции долготы Солнца (Белькович, 1986). Отсюда можно сделать следующий вывод: конечной целью обработки результатов наблюдений метеорных потоков является построение профилей изменений Q и s как функций долготы Солнца λ.
Литература:
(1986).’’О пространственной структуре метеорного потока Геминид.’’ Астрономический вестник. 20, №2. с.143-151.
Burns J. A., Lamy P. L., and Soter S. (1979). "Radiation forces on small particles in the solar system". Icarus, 40, 1-48.
Koschack R. and Rendtel J. (1990a). "Determination of spatial number density and mass index from visual meteor observations (I)". WGN, 18:2, 44-58.
Koschack R. and Rendtel J. (1990b). "Determination of spatial number density and mass index from visual meteor observations (II)". WGN, 18:4, 118-140.
Wikipedia (undated). "Poynting-Robertson effect".
Глава 2.
Физика разрушения метеорного тела в атмосфере Земли и образование
ионизированного метеорного следа
Рассматривается разрушение метеорного тела, а также формирование и диффузия ионизированного метеорного следа, водится понятие линейной электронной плотности ![]() и начального радиуса r0. Даются понятия диффузии ионизированного следа и характеристической высоты h0 метеорного потока.
и начального радиуса r0. Даются понятия диффузии ионизированного следа и характеристической высоты h0 метеорного потока.
1. Состав и структура частиц метеорных потоков.
Мы знаем, что метеориты, т. е., метеороиды достаточно большие, чтобы достичь поверхности Земли, состоят из углерода, силикатов или железа. Однако, нет метеоритов, которые ассоциировались бы с метеорными потоками. Это потому что большинство метеорных потоков являются продуктами дезинтеграции ядер комет и известно, что ядра комет состоят из первичного вещества Солнечной Системы: льдов, смешанных с
рыхлыми, легко распадающимися частицами с объёмной плотностью около 0,2-1 г/см3. Это подтверждается изучением микрометеоритов, наблюдаемых с помощью аппаратуры, установленной на космических аппаратах. Из-за своей рыхлой структуры, потоковые метеороиды разрушаются на частицы одного порядка величины и полностью разрушаются, не достигая поверхности Земли. И только небольшая часть метеорных потоков, которые являются продуктами разрушения астероидов после их столкновений, содержат фрагменты, которые могут избежать полной абляции в атмосфере и достигнуть поверхности Земли.
2. Процессы, сопровождающие вход метеороидов в атмосферу Земли
2.1 Атмосфера Земли
Так как абляция метеороидов имеет место в атмосфере Земли, необходимо рассмотреть модель атмосферы на метеорных высотах. Барометрическая формула определяет давление P(h) на высоте атмосферы h :
(1)
H- приведённая высота атмосферы, она определяется как
![]() (2)
(2)
Где R=8,314 Дж/моль∙K - универсальная газовая постоянная, T – температура атмосферы в градусах Кельвина, µ = 0,029 кг/моль – средняя молекулярная масса воздуха и g = 9,8 м/с2 – ускорение свободного падения. В первом приближении температура атмосферы T является константой в
интервале высот h в метеорной зоне. В случае если H константа p(h) определяется по формуле
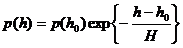 (3)
(3)
Таким образом, H – это интервал высот, в пределах которого давление атмосферы ![]() изменяется в
изменяется в ![]() раз. При использовании фактической модели атмосферы видно, что H немного зависит от высоты. В Таблице 1 приведены значения H для двух разных моделей атмосферы. Однако, эти величины подвержены также сезонным и суточным вариациям, и зависят от солнечной активности. Использование фиксированных
раз. При использовании фактической модели атмосферы видно, что H немного зависит от высоты. В Таблице 1 приведены значения H для двух разных моделей атмосферы. Однако, эти величины подвержены также сезонным и суточным вариациям, и зависят от солнечной активности. Использование фиксированных
значений H в пределах от 5,6- 5,8 км достаточно надёжно в нашем случае.
Таблица 1
h (км) | 80 | 85 | 90 | 95 | 100 | 105 |
H (COSPAR, км) H(ГОСТ, км) | 5,59 5,96 | 5,60 5,68 | 5,60 5,62 | 6,02 5,83 | 6.44 6,04 | 7,21 6,69 |
Действительные величины приведённой высоты H. Первая строка показывает значения в соответствии с COSPAR (1965), во второй строке ГОСТ 4401-81 Стандарт параметров атмосферы (1982). Однако необходимо иметь в виду, что истинные величины имеют суточные, сезонные и 11-летние изменения.
2.2 Процесс абляции
Метеороид, входящий в атмосферу Земли нагревается за счёт столкновения с молекулами атмосферы. Мелкие метеороиды прогреваются насквозь до начала интенсивного испарения, связи между составляющими его более плотными мелкими частицами разрушаются и метеороид рассыпается на более мелкие фрагменты приблизительно одного размера. Потом каждый фрагмент сталкивается с молекулами атмосферы, плавится и испаряется. Это так называемая метеорная модель “dustball”. Более массивные метеороиды не имеют достаточно времени, чтобы полностью рассыпаться в течении их полёта в атмосфере. Вместо этого их внешние слои частично плавятся и испаряются, но ядро остаётся нетронутым. Этот процесс дезинтеграции входящих в атмосферу метеорных тел называется абляцией.
2.3 Ионизация следа
Испарившиеся атомы метеороида продолжают движение относительно окружающей атмосферы со скоростью метеороида и, сталкиваясь с молекулами атмосферы, производят свободные электроны. Скорость производства свободных электронов пропорциональна скорости испарения частиц n:
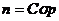 (4)
(4)
где C –некоторый коэффициент, σ – площадь поперечного сечения метеороида и p- атмосферное давление. В течении процесса абляции метеороида σ - уменьшается, а p – увеличивается. Число свободных электронов на единицу длины метеорного следа называется линейной электронной плоскостью α. Она изменяется вдоль метеорного следа как (Herlofson, 1948; Kaiser, 1953; Белькович 1971):
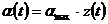 , (5)
, (5)
где
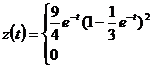
![]() (6)
(6)
Функция ![]() показана на Рис.1.
показана на Рис.1.
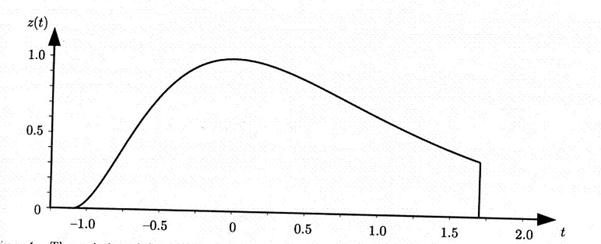
Рис 1. Функция ![]() . При t= 1,7 метеороид разогрелся достаточно, чтобы начался процесс абляции и началась ионизация атмосферы. При t= -ln 3 метеорное тело полностью испарилось. Обратите внимание, что t уменьшается в процессе входа метеорного тела в атмосферу.
. При t= 1,7 метеороид разогрелся достаточно, чтобы начался процесс абляции и началась ионизация атмосферы. При t= -ln 3 метеорное тело полностью испарилось. Обратите внимание, что t уменьшается в процессе входа метеорного тела в атмосферу.
В формуле (6) мы ввели относительную высоту t, как:
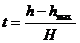 (7)
(7)
где h высота атмосферы (км) в рассматриваемой точке на следе, hmax – высота точки следа с максимальной линейной электронной плотностью αmax, и H – приведённая высота атмосферы. Введение относительной высоты ![]() позволяет нам использовать единую функцию z(t) для всех метеоров, зависящую только от одной переменной t.и не зависимую от зенитного угла χ метеора. Подобный же метеороид с зенитным углом χ создаст метеорный след с той же самой разницей высот в начальной и конечной точке. Таким образом его след будет длиннее на множитель
позволяет нам использовать единую функцию z(t) для всех метеоров, зависящую только от одной переменной t.и не зависимую от зенитного угла χ метеора. Подобный же метеороид с зенитным углом χ создаст метеорный след с той же самой разницей высот в начальной и конечной точке. Таким образом его след будет длиннее на множитель ![]() и скорость производства свободных электронов будет размазана по всей длине следа. Это означает, что:
и скорость производства свободных электронов будет размазана по всей длине следа. Это означает, что:
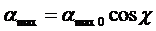 (8)
(8)
Рассмотрим вертикальный метеорный след, формируемый метеороидом с массой m (в кг) и скоростью v (в км/с). Максимальная линейная электронная плотность αmax0 (в m-1) получается из следующего эмпирического уравнения (Тохтасьев, 1977) с некоторыми поправками
![]() [в m-1] (9)
[в m-1] (9)
бъединяя все уравнения, полученные в этой части, мы получим общее уравнение линейной электронной плотности (в m-1) как функцию высоты:
![]() [в m-1] (10)
[в m-1] (10)
2.4. Радиус метеорного следа.
Испаряющиеся атомы имеют ту же скорость относительно окружающей атмосферы, что и метеороид, т. е. имеют высокую кинетическую энергию с начальной температурой, более высокой, чем температура атмосферы. Приблизительно после 10-3 с, последовательное столкновение с атмосферными молекулами, снижают температуру испарившихся атомов, и температура понижается до температуры окружающей атмосферы. Атомы разлетаются в различных направлениях от первоначального пути метеороида, и производят на своём пути свободные электроны. Результатом этого процесса является то, что ионизированный след имеет начальный радиус r0 почти мгновенно после возникновения следа. После этой начальной фазы, след продолжает расширяться за счет действия амбиполярной диффузии. Этот диффузионный процесс управляется электростатическими силами, которые заставляют электроны и ионы диффундировать с одинаковыми скоростями в электрически нейтральной атмосфере. Скорость диффузии электронов и ионов определяется коэффициентом амбиполярной диффузии D и зависит от свойств
атмосферы на рассматриваемой высоте. В результате изменение объемной плотности электронов как функцию радиуса в метеорном следе можно описать как
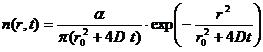 , (11)
, (11)
где n(r,t), число электронов в единице объема за время t с начала действия амбиполярной диффузии в точке метеорного следа на расстояние r от оси следа и α линейная электронная плотность в рассматриваемой точке следа
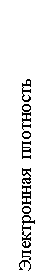
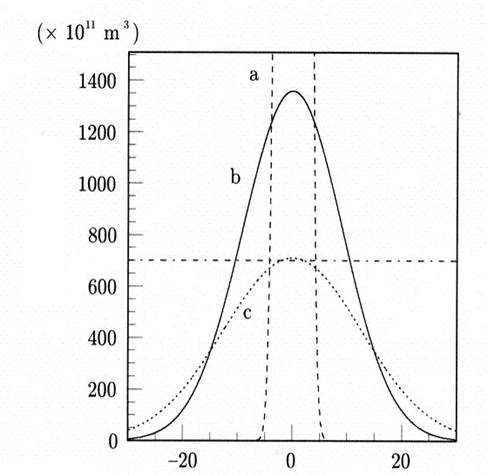
Рис 2-Объемная электронная плотность (число электронов на м3) как функция радиуса для нескольких радиальных срезов метеорного следа в различные моменты времени (a, b, c).
Следующие две форм5; Тохтасьев, 2006):
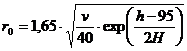 м (12)
м (12)
![]() м2/с, (13)
м2/с, (13)
где v это скорость метеора в км/с, h- высота в км и H – приведенная высота
атмосферы в км
.
3 Характеристическая высота метеорного потока h0
Рассмотрим метеороиды, входящие в атмосферу Земли с фиксированной скоростью, плотностью и фиксированным углом χ, как метеороиды, принадлежащие одному и тому же потоку в какое-то фиксированное время. Нам необходимо выбрать некоторую опорную высоту, от которой будет производиться отсчет для этой группы метеоров. Для этого мы выберем высоту, hmax как она была использована в формуле (10). Фактически, высота максимума ионизации на метеорном следе зависит не только от скорости, плотности и зенитного угла, но также и от массы метеороида: чем тяжелее частица, тем ниже высота максимума ионизации
метеорного следа. Однако, как мы отметили выше, метеороиды, которые могут быть зарегистрированы обычным метеорным радаром, разрушаются на маленькие фрагменты, которые имеют приблизительно одинаковую массу, и фрагменты испаряются отдельно. Максимальная линейная электронная плотность αmax и высота hmax ,таким образом, одинаковы для каждого из элементарных фрагментов. Это показано на Рис 3. (Белькович и др., 1999).Если метеороид разрушается на приблизительно одинаковые фрагменты, они все произведут максимальную линейную электронную плотность αmax на высоте hmax, которая является самой большой высотой максимума ионизации для метеоров этой группы. Мы обозначим эту высоту как h0 и назовем ее характеристической. Необходимо заметить, что характеристическая высота ![]() зависит от скорости метеороида, его плотности и зенитного угла радианта. Если выделить только зависимость от зенитного угла, тогда можно пользоваться эмпирической формулой (Тохтасьев.,1975):
зависит от скорости метеороида, его плотности и зенитного угла радианта. Если выделить только зависимость от зенитного угла, тогда можно пользоваться эмпирической формулой (Тохтасьев.,1975):
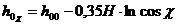 (14)
(14)
Где ![]() и
и ![]() характеристические высоты для метеороидов с одинаковыми скоростями и плотностями и соответственно зенитными углами χ и 0о. Эта формула также годится для других высот максимума ионизации отличных от характеристической (т. е. для микрометеороидов с большей массой, которые перед началом испарения не распадаются полностью на отдельные фрагменты):
характеристические высоты для метеороидов с одинаковыми скоростями и плотностями и соответственно зенитными углами χ и 0о. Эта формула также годится для других высот максимума ионизации отличных от характеристической (т. е. для микрометеороидов с большей массой, которые перед началом испарения не распадаются полностью на отдельные фрагменты):
![]() (16)
(16)
|
|
|
|
|
|

Рис 3. – изменение высоты 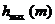 максимальной ионизации на метеорном
максимальной ионизации на метеорном
следе как функции массы метеороида m для фиксированных значений скорости v, плотности ρ и зенитного угла χ.
На Рис 3 показано как высота hmax(m) максимальной электронной плотности αmax(m) изменяется как функция массы m метеороида с фиксированной скоростью, плотностью и зенитным углом. Большинство наблюдаемых радиолокатором метеороидов разрушается на маленькие фрагменты, приблизительно одинаковой массы, что приводит к одинаковой высоте максимума ионизации h0 (характеристическая высота). Для самых маленьких масс метеорные частицы меньше этих фрагментов, так что они полностью расплавляются и падают как жидкие капли. С другой стороны, метеороиды с массами больше чем некоторая масса mk слишком велики, чтобы полностью разрушится на более мелкие фрагменты вначале процесса абляции. Начиная с этой массы, высота максимальной ионизации hmax(m) становится ниже, если m возрастает. Более точно (Белькович и др., 1999):
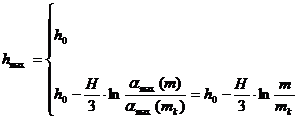 если
если 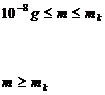 (16)
(16)
4. Заключение
С помощью приведенных в этой главе уравнений мы теперь можем для конкретного метеора полностью определить α(h) и n(r,t) используя только массу метеороида m, его скорость v, зенитный угол χ и высоту максимальной ионизации hmax. Последняя может быть найдена с по результатам видео наблюдений (см. раздел 2.1 стр.??)
Литература
(1971). Статистическая теория радиолокации метеоров.
Из-во КГУ. 104 с.
Belkovich O. I., Suleymanova S., and Tokhtasjev V. (1999) “Meteor height
distributions: a new look”. In Meteoroids 1998, Proceedings of the
International Conference held at Tatranska Lomnica, Slovakia,1998. p. 63-66. Astronomical Institute, Slovak Academy of Scinces, Bratislava.
Herlofson N. (1948) “The thory of meteor ionization”. Repts. Prog. Phys., 11, 444.
(1975) «Образование и распад метеорных следов» Взаимодействие метеорного вещества с Землёй и оценка притока метеорного вещества на Землю и Луну.- Душанбе, 1975 с. 100-107
(1977) «Шкалы масс для радиометеоров, визуальных и
фотографических метеоров» Всесоюзный симпозиум «Проблемы радиометеорных исследований атмосферы». Тезисы докладов.- Харьков, 1977. –с 26.
(2006) Личное сообщение.
Глава3
Физика отражения радиоволн от ионизированных следов метеоров при радиолокационных наблюдениях
Здесь рассматриваются различные механизмы отражения радиоволн от недоуплотненных и переуплотненных ионизированных метеорных следов, а также изменение амплитуды сигнала как функции времени для обоих случаев. Рассматривается также отражение радиоволн от метеорных следов, которые имеют промежуточную линейную электронную плотность.
1. Введение.
Отражения радиоволн от ионизированных метеорных следов могут быть двух типов: от недоуплотненных и переуплотненных следов в зависимости от электронной плотности следа. Здесь мы выведем формулы амплитуд сигнала, а так же их изменение с течением времени для обоих случаев, и изучим переход между обоими типами отражений.
2. Отражение радиоволн от недоуплотненных следов.
В первом случае, для недоуплотненных метеорных следов, объемная плотность свободных электронов в следе метеора мала, поэтому радиоволны могут полностью проникать в след без значительных помех и ослабления. В этом случае каждый свободный электрон следа переизлучает падающую радиоволну независимо: все свободные индивидуально реагируют на электрическое поле одной и той же радиоволны и все вместе когерентно рассеивают эту радиоволну.
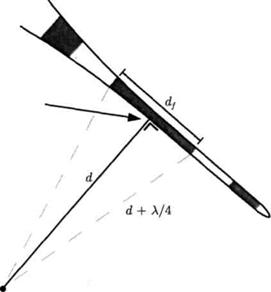
Та часть метеорного следа, которая дает наибольший вклад в мощность отраженного сигнала, ограничена несколькими зонами Френеля (см Рис. 1) в окрестностях отражающей точки, которая находится на основании перпендикуляра, опущенного на метеорный след из точки положения антенны радиолокатора. На практике достаточно рассматривать первую зону Френеля, как источник отраженной мощности. По-другому можно сказать, что отражение является зеркальным, то есть метеорный след действует как зеркало для радиоволн.
|
отражающая |
Рис. 1 – Зоны Френеля на метеорном следе. Если d-расстояние от радиолокатора до отражающей точки, то расстояние до краев первой зоны Френели должно быть ![]() . Длина первой зоны Френели –
. Длина первой зоны Френели –
После того как метеороид пройдет первую зону Френеля, амплитуда отраженных радиоволн достигает своего максимума и начинает уменьшаться за счет того, что на след в атмосфере действует диффузия. Уменьшение амплитуды является экспоненциальным (Кайзер,1953):
![]() (1)
(1)
где ![]() в вольтах на входе приемника) – является максимальной амплитудой, t-время в секундах,
в вольтах на входе приемника) – является максимальной амплитудой, t-время в секундах, ![]() постоянная времени (в секундах), заданная как:
постоянная времени (в секундах), заданная как:
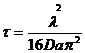 , (2)
, (2)
где ![]() - длина радиоволны (в метрах), и
- длина радиоволны (в метрах), и ![]() – коэффициент амбиполярной диффузии (м2/с), (см. раздел 2.4 на странице??). Изменение амплитуды сигнала во времени показано на Рис 2.
– коэффициент амбиполярной диффузии (м2/с), (см. раздел 2.4 на странице??). Изменение амплитуды сигнала во времени показано на Рис 2.
A(t)
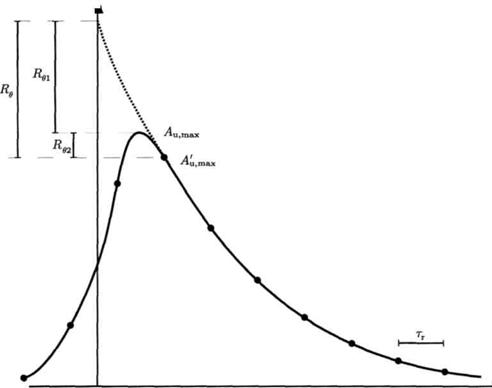
Рис. 2 Изменение амплитуды А(t) в зависимости от времени для недоуплотненного радиоэха, для идеального случая (точечная линия, ![]() ), и для реального случая с конечной скоростью метеороида и начальным радиусом(жирная лини). График иллюстрирует также эффект поправки амплитуды сигнала
), и для реального случая с конечной скоростью метеороида и начальным радиусом(жирная лини). График иллюстрирует также эффект поправки амплитуды сигнала ![]() за счет диффузии следа за время формирования главной зоны Френеля а также поправки
за счет диффузии следа за время формирования главной зоны Френеля а также поправки ![]() за счет того, что импульс сигнала радиолокатора с периодом повторения
за счет того, что импульс сигнала радиолокатора с периодом повторения ![]() может не совпадать с моментом максимума амплитуды.
может не совпадать с моментом максимума амплитуды.
Величина ![]() максимальной амплитуды радио эха при отражении радиоволн от недоуплотненного метеорного следа, получена Т. Кайзером (Кайзер, 1953) и уточнена Бельковичем (Белькович, 1971):
максимальной амплитуды радио эха при отражении радиоволн от недоуплотненного метеорного следа, получена Т. Кайзером (Кайзер, 1953) и уточнена Бельковичем (Белькович, 1971):
![]() , (3)
, (3)
где ![]() - линейная электронная плотность следа (
- линейная электронная плотность следа (![]() ) в отражающей точке,
) в отражающей точке, ![]() - коэффициент отражения для недоуплотненных метеорного следа,
- коэффициент отражения для недоуплотненных метеорного следа, ![]() (м).- классический радиус электрона.
(м).- классический радиус электрона. ![]() - поправочный коэффициент, речь о котором пойдет далее в этом тексте. Наконец, F включает в себя влияние геометрии отражения и свойства радиоприемника и, рассчитано следующим образом (Kaiser, 1953):
- поправочный коэффициент, речь о котором пойдет далее в этом тексте. Наконец, F включает в себя влияние геометрии отражения и свойства радиоприемника и, рассчитано следующим образом (Kaiser, 1953):
![]() (4)
(4)
Где R - входное сопротивление радиоприемника (в ![]() ),
), ![]() - длина волны (м), d - расстояние (м) от радиолокатора до отражающей точки,
- длина волны (м), d - расстояние (м) от радиолокатора до отражающей точки, ![]() и
и ![]() - коэффициенты усиления передающей и приемной антенн в направлении отражающей точки.
- коэффициенты усиления передающей и приемной антенн в направлении отражающей точки.
Рассмотрим теперь коэффициент коррекции ![]() , который упомянули
, который упомянули
раннее. Фактически наблюдаемая максимальная амплитуда эха метеора ![]() зависит от диффузии метеорного следа за время формирования главной зоны Френеля и начального радиуса
зависит от диффузии метеорного следа за время формирования главной зоны Френеля и начального радиуса ![]() уменьшает амплитуду эха. Эффект более силен для малой скорости метеороида, большого начального радиуса и быстрой диффузии. Другой фактор, значительно влияющий на наблюдаемую максимальную амплитуду, это ограниченная частота повторения импульса радиолокатора. Этот фактор не влияет при использовании радиолокатора с непрерывным излучением, или с высокой частотой повторения импульсов. Для старых радиолокационных станций, где время между двумя последующими импульсами может быть значительно, его необходимо учитывать. Поправочный коэффициент
уменьшает амплитуду эха. Эффект более силен для малой скорости метеороида, большого начального радиуса и быстрой диффузии. Другой фактор, значительно влияющий на наблюдаемую максимальную амплитуду, это ограниченная частота повторения импульса радиолокатора. Этот фактор не влияет при использовании радиолокатора с непрерывным излучением, или с высокой частотой повторения импульсов. Для старых радиолокационных станций, где время между двумя последующими импульсами может быть значительно, его необходимо учитывать. Поправочный коэффициент ![]() статистически вносит поправки за эти два эффекта:
статистически вносит поправки за эти два эффекта:
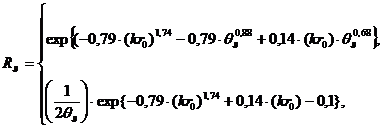 если
если ![]() (5)
(5)
где ![]() ,
, ![]() - начальный радиус,
- начальный радиус,
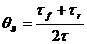 , (6)
, (6)
где ![]() - период зондирующих импульсов радиолокатора и
- период зондирующих импульсов радиолокатора и ![]() - время спада сигнала, отраженного от недоуплотненного метеорного следа на характеристической высоте
- время спада сигнала, отраженного от недоуплотненного метеорного следа на характеристической высоте ![]() , - время, за которое метеорное тело проходит половину главной зоны Френеля,
, - время, за которое метеорное тело проходит половину главной зоны Френеля,
![]() . (7)
. (7)
Здесь (с), ![]() (м с-1)- скорость метеороида,
(м с-1)- скорость метеороида, ![]() (м) – расстояние от радиолокатора до отражающей точки,
(м) – расстояние от радиолокатора до отражающей точки, ![]() (м) - длина волны радиолокатора.
(м) - длина волны радиолокатора.
2 Рассеивания на переуплотненных метеорных следах.
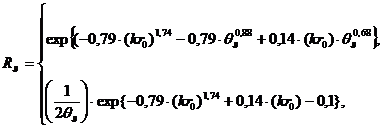 если
если ![]() (5)
(5)
где ![]() ,
, ![]() - начальный радиус,
- начальный радиус,
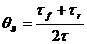 , (6)
, (6)
где ![]() - период зондирующих импульсов радиолокатора и
- период зондирующих импульсов радиолокатора и ![]() - время спада сигнала, отраженного от недоуплотненного метеорного следа на характеристической высоте
- время спада сигнала, отраженного от недоуплотненного метеорного следа на характеристической высоте ![]() , - время, за которое метеорное тело проходит половину главной зоны Френеля,
, - время, за которое метеорное тело проходит половину главной зоны Френеля,
![]() . (7)
. (7)
Здесь (с), ![]() (м с-1)- скорость метеороида,
(м с-1)- скорость метеороида, ![]() (м) – расстояние от радиолокатора до отражающей точки,
(м) – расстояние от радиолокатора до отражающей точки, ![]() - длина волны радиолокатора.
- длина волны радиолокатора.
3 Отражение радиоволн от переуплотненных метеорных следов
![]()
Если объемная электронная плотность в следе метеора выше, чем критическая плотность, то радиоволны не будут способны проникнуть через ось следа, где электроны тесно взаимодействуют друг с другом. Центральная часть следа теперь ведет себя по отношению к падающей волне как металлический цилиндр радиусом rc, от поверхности которого отражаются радиоволны. Первоначально, величина rc увеличивается за счет эффекта диффузии (см. Рис. 3). В течние этого периода, амплитуда эха также увеличивается. Электронная плотность в центре следа, однако, уменьшается, уменьшается и rc пока не станет равным 0. Эхо, следовательно, ослабнет тоже и исчезнет.
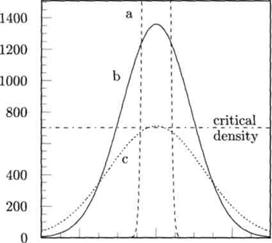
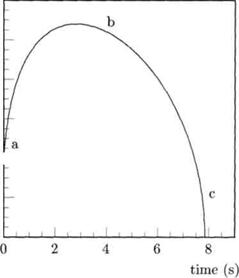
Рис. 3 – Амплитуда радиоэха от переуплотненного метеорного следа. Слева показана диффузия метеорного следа, где объемная электронная плотность n (r, t) (м )показана в разрезе следа в моменты времени а, b, и c. Справа - изменение критического радиуса rc следа (м), для интервалов времени, обозначенных a, b и c![]()
.
Максимальная амплитуда ![]() (в) для эха от переуплотненного следа метеора на входе приемника радара задается уравнением (Kaiser, 1953):
(в) для эха от переуплотненного следа метеора на входе приемника радара задается уравнением (Kaiser, 1953):
![]() , (8)
, (8)

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 |