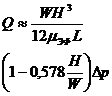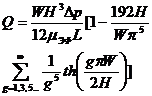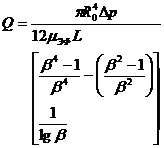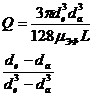Диаграмма Хэдстрема позволяет рассчитывать по формуле (234) Дарси-Вейсбаха линейные потери давления в трубе при течении ньютоновских жидкостей и сред Бингама-Шведова. Однако вязкостные свойства всех пищевых сред описать этими двумя линейными реологическими моделями нельзя. Можно получить общий алгоритм построения формул вида (236) и (238) для различных неньютоновских жидкостей. Воспользуемся следующими формулами, которые были выведены раньше:
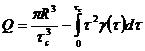 (240)
(240)
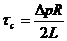 (241)
(241)
Из формул (241) и (234) получим:
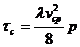 (242)
(242)
По определению (235) и формуле (240) можно записать:
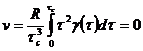 (243)
(243)
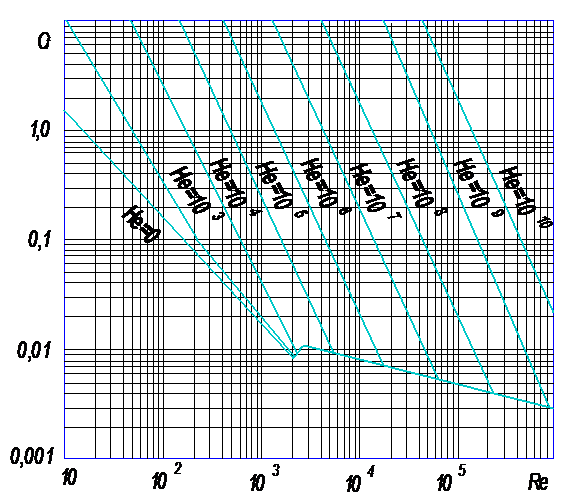
Рис. 32. Диаграмма Хедстрема.
или, с учетом формулы (242),
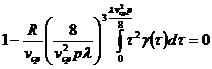 (244)
(244)
Формула (244) позволяет получать зависимости вида (236) и (238). Например, для ньютоновской жидкости ![]() . Подставив последнее выражение год знак интеграла в формуле (244) и проведя интегрирование, получим выражение вида:
. Подставив последнее выражение год знак интеграла в формуле (244) и проведя интегрирование, получим выражение вида:
 (245)
(245)
что с учетом определения (237) эквивалентно формуле (236). Для жидкости Оствальда-де-Вале из формулы (244) можно получить выражение вида:
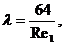 (246)
(246)
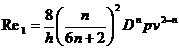 (247)
(247)
Формулу (244) можно считать обобщением метода Хэдстрема в части аналитических решений; она позволяет построить аналогичные диаграмме Хэдстрема диаграммы для различных неньютоновских жидкостей. Если такие диаграммы не построены, то можно расчет перепадов давлений производить аналитически по формулам (244) и (234). Правда, такой путь определения величины Δр иногда становится несколько искусственным. Например, аналог формулы (238) для среды Гершеля-Балкли настолько сложен, что в этом случае целесообразнее просто найти Δр из формулы расхода, применяя итерационные численные методы и ЭЦВМ.
§ 17. ТЕЧЕНИЕ ПИЩЕВЫХ МАСС ПО НАКЛОННЫМ ПЛОСКОСТЯМ
В ряде технологических процессов пищевых производств реализуются операции (нанесение покрытий, глазировка и т. п."), при которых иеныотоновские пищевые среды стекают под действием собственного веса по различным поверхностям. Для анализа этих операций необходимо знать зависимости между динамическими, кинематическими и геометрическими параметрами потока, свойствами среды и геометрией поверхности.
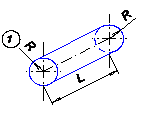
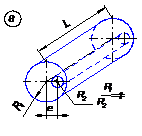
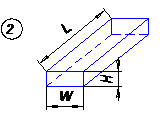
Рассмотрим простейшую модель этого класса задач [1, 2]—ламинарное течение по бесконечной наклонной плоскости, полагая пренебрежимыми краевые эффекты на свободной поверхности (поверхностное натяжение, волны, трение о воздух), но учтем возможность пристенного проскальзывания и неныотоновских свойств жидкости. Схема задачи приведена на рис. 33.
Вырежем мысленно из потока слой жидкости толщиной Δу, длиной L, и шириной W и составим уравнение равновесия сил, действующих на слой в проекциях на ось х:
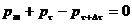 (248)
(248)
где Рm — проекция, главного вектора массовых сил на ось х,
pτpτ+Δτ —главные вектора сил вязкого трения на поверхностях (х, у, z) и (х, у + Δy, z).
Уравнение (248) запишем в виде (см. рис. 33):
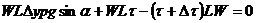 (249)
(249)
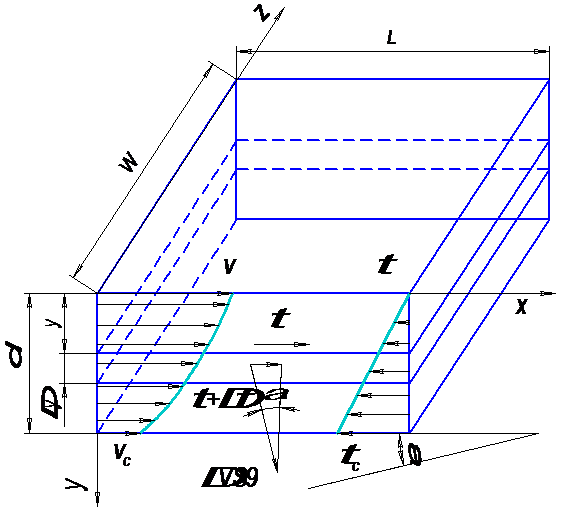
Рис. 33. Схема течения пищевых сред по наклонным плоскостям.
где р — плотность среды,
g — ускорение свободного падения или
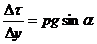 (250)
(250)
В данном случае:
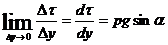 (251)
(251)
Интегрируя (251)
 (252)
(252)
где используется условие 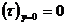 , получим
, получим
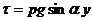 (253)
(253)
Формула (253) позволяет построить эпюру касательных напряжений (рис. 33) и записать выражение
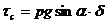 (254)
(254)
и
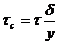 (255)
(255)
Если известен реологический закон течения жидкости
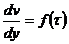 (256)
(256)
то с помощью формулы (253) можно записать интеграл
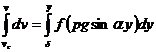 (257)
(257)
или
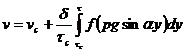 (258)
(258)
где Vc — скорость скольжения по стенке.
В формуле (258), используя (255), можно сделать замену переменных:
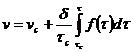 (259)
(259)
Расход жидкости Q определяем по формуле
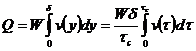 (260)
(260)
Введем обозначение
![]()
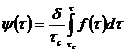 (261)
(261)
и проведем интегрирование (260) по частям:
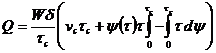 (262)
(262)
Заметив по формуле (261), что
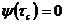 (263)
(263)
и
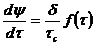 (264)
(264)
перепишем (262) окончательно в виде:
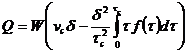 (265)
(265)
Формула (265) аналогична модификации формулы Рабиновича-Муни для капиллярного вискозиметра и наклонную плоскость можно использовать в качестве вискозиметра. Действительно, следуя теории капиллярных вискозиметров [3], введем обозначение эффективного коэффициента по Олдронду:
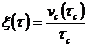 (266)
(266)
и функцию
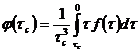 (267)
(267)
Тогда формула (265) может быть записана в виде:
 (268)
(268)
При наличии проскальзывания кривые течения в координатах ![]() и
и ![]() расслаиваются для различных толщин δ, что позволяет построить семейство прямых в координатах
расслаиваются для различных толщин δ, что позволяет построить семейство прямых в координатах ![]() и
и ![]() при фиксированных значениях
при фиксированных значениях ![]() . Это семейство прямых определяет функции
. Это семейство прямых определяет функции ![]() и
и ![]() , поскольку
, поскольку ![]() представляют собой тангенсы углов наклона прямых,
представляют собой тангенсы углов наклона прямых, ![]() — ординаты пересечения прямых с осью
— ординаты пересечения прямых с осью 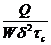 .
.
Функция ![]() позволяет рассчитать скорости сдвига
позволяет рассчитать скорости сдвига ![]() на стенке, что можно показать дифференцированием уравнения (267) по переменной
на стенке, что можно показать дифференцированием уравнения (267) по переменной ![]() . При этом получаем формулу вида:
. При этом получаем формулу вида:
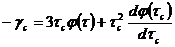 (269)
(269)
Если проскальзывание отсутствует, то скорость сдвига ![]() , получим непосредственно дифференцируя выражения (265) но при
, получим непосредственно дифференцируя выражения (265) но при ![]() :
:
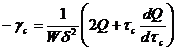 (270)
(270)
Формулы скоростей и расходов для конкретных неньюто-новскпх пищевых материалов просто получить оперируя выражениями (258), (259) и (265), если известен вид реологического закона (256).
§ 18. РАСЧЕТ ВЫДАВЛИВАЮЩИХ МАШИН (ЭКСТРУДЕРОВ) И ИХ РАБОЧИХ ОРГАНОВ
Эксгрудеры или выдавливающие прессы состоят из нагнетателя и формующего инструмента. В системе нагнетатель-матрица можно видеть аналогично с электрической системой генератор-потребитель, с системами вентилятор-воздуховоды, насосы-трубопроводы. Расчет всех этих систем имеет аналогию и для системы нагнетатель-матрица производится по методу совмещенных расходно-напорных характеристик нагнетателя и матрицы.
Расходно-напорная характеристика представляет собой либо график в координатах расход-давление, либо аналитическое выражение, связывающее эти величины с геометрическими и кинематическими параметрами нагнетателя или матрицы. Вообще, чем больше давление перед каналом матрицы со стороны нагнетателя, тем больше расход выдавливаемой среды. Рост же давления на выходе из нагнетателя приводит к снижению производительности (расхода) нагнетателя.
Точка пересечения расходно-напорных характеристик матрицы и нагнетателя дает производительность экструдера и давление в предматричной камере. Эти величины необходимы для включения экструдера в поточные линии и прочностных расчетов деталей экструдера.
Конструкций нагнетателей большое количество (цилиндр с поршнем, червяк, шестеренный насос и т. д.) и задача построения расходно-напорной характеристики нагнетателя требует каждый раз специального рассмотрения. Матрица же представляет собой более унифицированный элемент машины. Если матрица состоит из цилиндрических каналов круглого пли щелевого сечения, то можно в расчетах использовать формулы, полученные в предыдущих параграфах. В некоторых случаях матрицы с более сложными каналами можно представить расчетной схемой с более или менее эквивалентным набором простейших круглых или щелевых каналов, конечно, при этом приходится пренебрегать местными сопротивлениями на переходах от одной формы канала к другой, а также входовыми и выходными эффектами, которые для течения пищевых сред сравнительно мало изучены.
Возникающие в общем случае задачи трехмерного течения неньютоновских жидкостей иногда очень сложны, что заставляет в практических расчетах использовать упрощения либо в форме канала, либо в реологической модели среды, или же прибегать к численным методам. В расчетах сложных каналов практически очень часто используются гидродинамические формулы, полученные с помощью простейшей модели ньютоновской жидкости. В эти формулы подставляют величину эффективной вязкости, определенную под действительной кривом течения при какой-то эффективной усредненной скорости сдвига.
Определение эффективной скорости сдвига не является тривиальной задачей и при удачном выборе этой величины метод эффективной вязкости может дать точные количественные результаты. Покажем это на простом примере течения степенной жидкости в канале круглого сечения. Расходно-напорная характеристика в этом случае имеет вид:
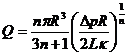 (271)
(271)
где Q — расход,
Δр — перепад давлений,
R, L —радиус и длина канала,
n, к — реологические константы среды.
Если величину эффективно скорости сдвига рассчитать по формуле вида:
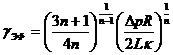 (272)
(272)
а эффективную вязкость, используя ее определение, и вид реологического закона течения степенной жидкости по формуле вида:
![]() (273)
(273)
то при подстановке в формулу Пуазейля вида:
![]() (274)
(274)
выражений (273) и (272) получим точную формулу (271). Этот пример показывает, что метод эффективной вязкости не всегда является чем-то весьма приближенным и может давать точные результаты. Однако для сложных по конфигурации каналов и усложненных моделей нет общего алгоритма построения таких точных формул для эффективной скорости сдвига как формула (272).
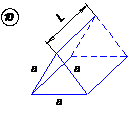
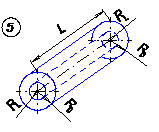
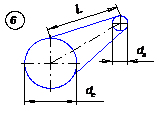
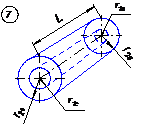
На рис. 34 приведены формулы для расчета течения ньютоновской жидкости в различных каналах, которые можно использовать для расчета каналов матриц по методу эффективной вязкости. В случае очень сложных каналов и повышенных требований к точности расчета необходимо решать соответствующие задачи численно на ЭЦВМ или же проводить имитационные экспериментальные исследования на моделях матриц и каналов.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| S, P – площадь и периметр поперечного сечения
|
|
| ||
|
| ||
| Формула №6 при
|
Рис. 34. К расчету формующего инструмента.
§ 19. РАСХОДНО-НАПОРНАЯ ХАРАКТЕРИСТИКА
ЧЕРВЯЧНОГО НАГНЕТАТЕЛЯ (РАБОЧЕГО ОРГАНА
ЭКСТРУДЕРА) ПО УПРОЩЕННОЙ
ГИДРОДИНАМИЧЕСКОЙ ТЕОРИИ
Рассмотрим построение расходно-напорной характеристики нагнетателя на примере червячного нагнетателя, которые широко распространены в пищевой промышленности.
В упрощенной гидродинамической теории червячных нагнетателей сложный межвитковый канал червяка (рис. 35а) заменяют расчетной схемой в виде прямоугольного канала (рис. 356) с одной подвижной верхней стенкой. При этом использован принцип обращения движения червяка и цилиндра, в котором вращается червяк. Полагают мысленно, что червяк неподвижен, а вращается цилиндр с угловой скоростью червяка.

Рис. 35. Расчетная схема червячного нагнетателя.
Ширина канала W и скорость верхней стенки VZ определяется тогда формулами вида:
![]() (275)
(275)
![]() (276)
(276)
где S — шаг винтовой линии,
φ — угол подъема винтовой липни,
V — линейная окружная скорость гребня пера червяка,
ω — угловая скорость червяка,
R — внешний радиус червяка,
n — число оборотов червяка в минуту.
Полагая, что глубина канала Н мала по сравнению с шириной W стенами, и записать краевую задачу, аналогичную задаче (211), (212) из § 14:
![]() (277)
(277)
![]() (278)
(278)
![]() (279)
(279)
![]() (280)
(280)
Подставив закон течения Ньютона (278) в дифференциальное уравнение (277) и проведя дважды интегрирование, получим
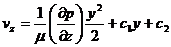 (281)
(281)
Константы интегрирования С1, и С2 находим с помощью краевых условий (279) и (280):
![]() (282)
(282)
![]() (283)
(283)
Тогда формула (281) приобретает вид:
![]() (284)
(284)
Формулу расходно-напорной характеристики получим, проведя интегрирование
 (285)
(285)
Подставив формулу (284) в интеграл (285), получим.
![]() (286)
(286)
Пользуясь основной формулой теории червячных нагнетателей (286), легко реализовать метод совмещенных характеристик. ПУСТЬ характеристика матрицы имеет вид:
![]() (287)
(287)
где к — коэффициент, характеризующий геометрию каналов матрицы и вязкостные свойства перерабатываемого материала,
Δр — давление в предматрице.
Формулу (286) можно представить в виде:
![]() (288)
(288)
учитывая обозначения
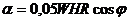 (289)
(289)
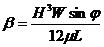 (290)
(290)
где L — длина червяка.
Совместное решение уравнений (287) и (288) дает производительность червячного пресса и давление в предматричной камере:
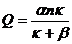 (291)
(291)
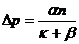 (292)
(292)
Более сложная теория червячных прессов излагается в специальной литературе [1, 2]. Данную здесь теорию можно использовать в первом приближении, если перерабатываемая среда обладает неньютоновскими свойствами. В этом случае применяют идею расчетов по эффективной вязкости, а эффективную скорость сдвига ![]() можно рассчитать по формуле:
можно рассчитать по формуле:
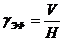 (293)
(293)
Если условие Н > W не выполняется, то необходимо учитывать влияние боковых стенок межвиткового канала на поток. Это достигается при решении гораздо сложной задачи, чем изложенная выше. Получаемые при этом конечные формулы имеют вид:
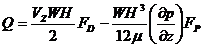 (294)
(294)
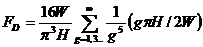 (295)
(295)
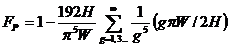 (296)
(296)
Функции FD (H/W) и FP(H/W) даются в специальной литературе в виде графиков [1]. Еще более усложняется задача получения расходно-напорной Характеристики червячного нагнетателя, если межвитковый канал имеет переменное по длине червяка сечение и это сечение нельзя заменить прямоугольной схемой канала.
Однако, несмотря на значительные упрощения при выводе формулы (286), она позволяет конструктору анализировать влияние на режим работы геометрических и кинематических параметров червячного пресса.
§ 20. УПРАВЛЯЮЩАЯ РЕОЛОГИЯ И ИМИТАЦИОННАЯ РЕОМЕТРИЯ
В ряде предыдущих параграфов были рассмотрены некоторые вопросы расчета пищевого оборудования на стадии учета реологических свойств перерабатываемых пищевых материалов. Однако роль физико-химической механики в пищевой промышленности далеко не исчерпывается использованием реологии в этих расчетах. Другим важным направлением является разработка методов управляющей реологии.
Основные аспекты управляющей реологии и ее роль в оптимизации и интенсификации технологических процессов формирования структуры пищевых масс рассмотрены в книге и [1]. Основываясь на исследованиях физико-химической механики процессов массопереноса и массообмена в сложных дисперсных системах, указываются пути резкой интенсификации многих процессов в пищевой промышленности. В целом эта интенсификация достигается максимальным увеличением активной поверхности, на которых происходят различные технологические процессы, в. гетерогенных пищевых системах за счет предельного разрушения структуры на начальных стадиях технологической переработки, а также стимуляцией специальными методами процессов на границах фаз. Используются вибрирующие рабочие органы и поверхностно-активные вещества, создаются в материалах состояния псевдосжижения и псевдокипения. Более подробно с этими моментами управляющей реологии можно ознакомиться в книге названных выше авторов [1].
Важным направлением совершенствования пищевой промышленности является создание поточных линий с автоматизированными системами управления. Здесь тоже определенную роль может сыграть реология. Дело в том, что в течение различных тепловых, химических и микробиологических процессов пищевой промышленности, как правило, меняют реологические параметры перерабатываемых продуктов. Следовательно, можно для контроля и управления процессами создать датчики, основанные на измерении реологических параметров перерабатываемых материалов. В качестве примера можно привести автоматическую систему обеспечения постоянных вязкостных свойств теста для хрустящих хлебцев (рис. 36).
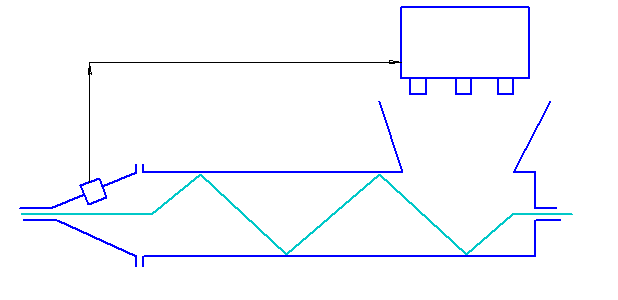
Рис. 36 Схема консистентно-статирования теста.
Если в силу естественной вариации свойств муки уменьшатся вязкостные свойства теста, то это приведет к снижению давления на выходе из сместителя 3 и сигнал от датчика давления 1 будет подай на механизмы управления дозатором ингредиентов 2. В результате будет уменьшено, допустим, количество подаваемой в смеситель жидкой фазы и вязкость опять достигнет требуемой величины. Последняя должна быть постоянной, иначе нарушится процесс размазывания теста на конвейер печи и хрустящие хлебцы не будут получаться требуемого качества. Описанная система, в сущности, представляет собой капиллярный вискозиметр непрерывного действия, встроенный в технологический поток, хотя в данном случае и не измеряется непосредственно вязкость теста.
Легко себе представить аналогичную систему управления консистенцией материала, где вместо управляющего технологического параметра будет не влажность, а температура. В качестве датчика также можно использовать ротационные, вибрационные и другие вискозиметры или реометры. Важно лишь знать, в каких пределах в относительных единицах реометра-датчика обеспечивается качественное протекание технологического процесса. В результате исследования, например, мясных фаршей с сотрудниками предлагает такие «эталонные» реологические параметры, позволяющие обоснованно управлять технологическими процессами.

Дальнейшее развитие управляющей реологии в этом направлении неизбежно приведет к широкому использованию кибернетических методов теории распознавания образов, создания автоматических систем управления, обладающих свойствами обучения и адаптации и включающих в себя ЭВМ. Именно в пищевой промышленности перерабатываемые материалы обладают значительной стохастичностыо свойств из-за влияния многочисленных факторов, и в сфере производства сырья в сельском хозяйстве, и в процессе транспортирования и хранения. Естественно, машины - переработки таких продуктов должны гибко реагировать на изменение свойств сырья, обеспечивая качественную переработку сырья и требуемые свойства конечного продукта. На производстве пока это достигается во многих случаях лишь обучением квалифицированных рабочих, которые на основе органолептических показателей управляют процессами переработки.
Во многих случаях конструирования пищевых масс возникают непреодолимые теоретические трудности описания реологических процессов. Тогда целесообразнее проводить имитационные реологические исследования. Параметры узла, расчет которого вызывает затруднения, варьируют в определенных пределах, составляют по теории планирования экспериментов план испытаний, проводят непосредственно имитационный эксперимент, результаты которого обрабатывают методами дисперсионного анализа. Оценив, таким образом, экспериментально влияние параметров узла на процесс обработки, же более обоснованно разрабатывают окончательную конструкцию. В конечном счете этот трудоемкий путь создания новой машины оказывается более экономным, чем путь интуитивной доводки конструкции, которая может быть принципиально плохой.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 |