(122)

(123)

(124)

окончательно

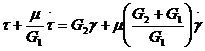(125)

Вспомним первый вариант уравнения ОЛТ. Теперь мы получили принципиально тот же вид при других значениях постоянных коэффициентов. Но характер этих коэффициентов (размерности, например) тот же.

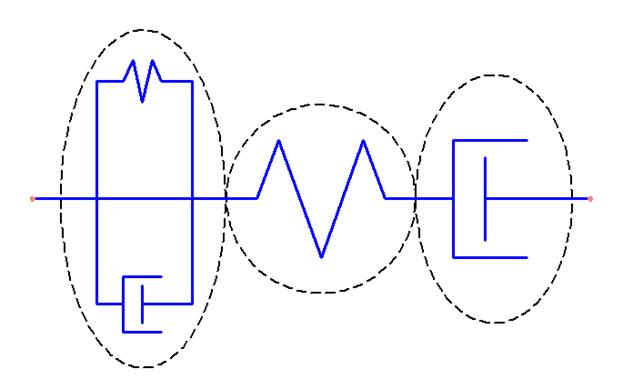
Вернемся к прерванному рассуждению о совершенствовании механической модели на основании введения уточнений, приближающих поведение к поведению реальных материалов. Модель тела Кельвина, например, дала возможность учесть имеющую место в реальном материале запаздывающую упругость, модель тела Максвелла — релаксацию напряжений. Модель ОЛТ учитывает и то и другое. Но вот только что, рассматривая кривую кинетики деформации для ОЛТ, мы пришли к выводу об обратимости деформаций. В реальном мире гораздо чаще встречаются материалы, которые после разгрузки не возвращаются к первоначальным размерам. Надо это обстоятельство учесть при построении модели, что и сделано в следующей (после ОЛТ) по сложности модели тела Бюргерса. В нее для исправления отмеченного недостатка введен последовательно соединенный элемент Ньютона (рис. 18).

Рис. 18. Механическая модель тела Бюргерса

Это теперь уже 4-х параметрическая модель. Таким обра­зом, реологическое уравнение тела Бюргерса будет иметь не 3 как у ОЛТ, а 4 реологических характеристики. Пред­лагаем вновь получить математическую модель символичес­ким методом.

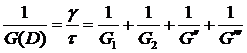(126)

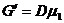; ; (127)

(128)

(129)

Это и есть уравнение тела Бюргерса. Кроме того, что в нем 4 реологических константы, следует отметить, что впер­вые в реологическом уравнении присутствуют, кроме первых производных напряжений и деформаций и вторые их произ­водные.

Можно, идя по этому пути, и дальше совершенствовать модели, но поскольку нас интересует, в конце концов, реше­ние инженерных задач, с доведением расчетов до числа, не всегда целесообразно еще более уточнять модель, ибо это мо­жет привести к резко более трудному или просто неразреши­мому варианту.

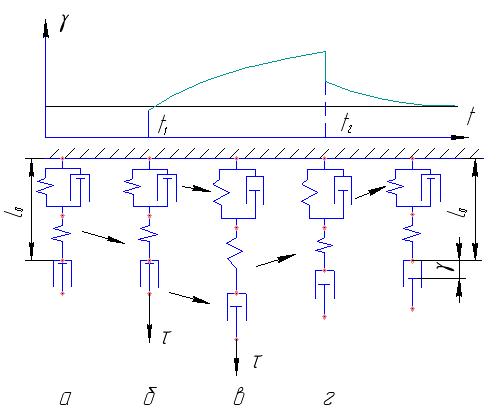
Рис.19. Кривая кинетики деформации тела Бюргерса (стрелки показывают места происходящих изменений деформации)

а – нет нагрузки, б – приложено напряжение, в – ползучесть, г - сняли напряжение.

Для примера анализа вида кривых кинетики деформации с помощью механической модели приведем без комментариев рисунок (рис. 19), аналогичный тому, который мы делали, изучая характер кинетики деформации в случае ОЛТ.

Теперь несколько слов о другом, весьма распространенном в инженерной практике, случае усложнения моделей с целью их совершенствования, т. е. с целью лучшего описания осо­бенностей поведения реальных материалов, моделируемых 'этими моделями.

Речь пойдет об обобщенном теле Максвелла и обобщен­ном теле Кельвина.

Соединять последовательно два (или несколько) элемен­тов Максвелла или соединять параллельно тела Кельвина не­целесообразно. Это не даст качественно новой картины. А вот соединить параллельно несколько тел Максвелла — это уже полезно (так же как и соединять параллельно тела Кель­вина).

Полученное таким путем (рис. 20) обобщенное тело Максвелла не следует экспоненциальному закону релаксации с определенным временем релаксации (например, для первого элемента. релаксация шла бы по экспоненте, определяемой временем релаксации 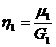, а ведет себя как более сложное тело, релаксирующее по совокупности кривых, характеризую­щихся различными временами релаксации. Эта совокупность характеризует свойства полученной модели и называется она спектром (дискретным или непрерывным) времен релаксации.

Аналогично строится обобщенное тело Кельвина, в модели которого последовательно соединен ряд элементов Кельвина и свойства которого характеризуются спектром времен за­паздывания.

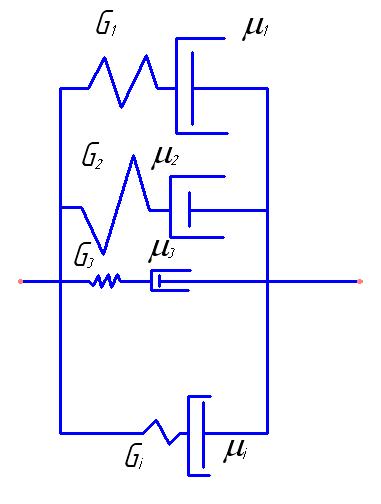
Рис.20. Механическая модель обобщенного тела Максвелла.

До сих пор мы говорили о моделях сложных тел, сочетаю­щих вязко-упругие свойства.

Для завершения разговора о моделях, описывающих с той или иной степенью точности свойства реальных материалов, нам остается обсудить модель тела, обладающего сложным комплексом упруго-вязко-пластичных свойств.

Таковым реальным телом, модель которого мы будем сей­час конструировать, является мучное тесто.

Реологическую модель мучного теста предложили в 30-е годы Шоффилд и Скотт-Блер.

Изучая поведение мучного теста, они установили вначале у образца теста, ведущего себя как упругое тело, наличие остаточных (после снятия растягивающих нагрузок) удли­нений. Следующая серия опытов показала, что упругое вос­становление образца мучного теста уменьшается с ростом времени действия нагрузок. Тесто стало, таким образом, по­ходить на тело Максвелла, ибо уменьшение упругого восста­новления объяснялось, как выяснили исследователи, наличием релаксации напряжений. Последующие опыты показали, что есть такое значение растягивающих напряжений, при котором скорость удлинения становится равной нулю. Тесто стало теперь обладать и свойствами тела Сен-Венана. Вскоре обна­ружено было и явление запаздывающей упругости. И так далее.

В конце концов и Скотт- останови­лись на пятипараметрическом уравнении, представляющем собой реологическую модель мучного теста.

где А, В, С, D, τ0 — реологические характеристики мучного теста для случая описания его поведения с помощью уравнения Шоффилд-Скотт-Блера.

§ 8. ОБЩИЕ ВОПРОСЫ РЕОМЕТРИИ

Реометрические исследования проводят, когда возникает необходимость определения как реологических (структурно-механических) свойств реальных пищевых материалов, так и характера их взаимодействия с рабочими органами и канала­ми перерабатывающих машин. Иными словами, реометрию пищевых материалов можно определить как совокупность приборов и методов для измерения реологических свойств пи­щевых материалов, определения структурных, кинематических и динамических характеристик взаимодействия рабочих орга­нов пищевых машин с пищевыми материалами и определения изменений реологических свойств материалов при реализации тепловых, химических и других немеханических технологиче­ских процессов переработки.

Совокупность объектов реологических исследований в пи­щевой промышленности охватывает широкий диапазон агре­гатных состояний материалов, начиная от твердых - хрупких тел (сухие макаронные изделия) и кончая маловязкими жид­костями (яблочный сок без мякоти). Это, а также разнообра­зие целей реологических исследований, требует применения исключительного разнообразия приборов (по принципам дей­ствия и конструктивным особенностям). Некоторое представ­ление о приборах реометрии дает рис. 21.

Широкое применение в пищевой реометрии находят рота­ционные вискозиметры (позиция № 10, 11, 12, 13, 16, 18, рис. 21), капиллярные вискозиметры (позиция № 23, 24, 25, 26, 27, 28), вискозиметры с падающим шариком (позиция № 19, 20, 21, 22), приборы типа Вейнберга, Толстого, Николае­ва с тангенциально смещающимися пластинами (позиция № 7), приборы типа Вейлера-Ребиндера (поз. № 9), кони­ческие и другие пластометры (поз. № 8, 6), приборы одноос­ного сжатия-растяжения (поз. № 1), приборы прессования в замкнутых объемах (поз. № 32).

Для подробного знакомства с конструкциями реометров следует обратиться к специальной литературе [1—7]. Заме­тим при этом, что характеризуя различные конструкции лишь важнейших из ротационных приборов, авторы [1] описали около ста конструкций. Естественно возникает вопрос, а не является ли конструктивное разнообразие реометров продук­том исторического развития реометрии, и не существуют ли универсальные приборы, позволяющие определить всю сово­купность реологических свойств испытуемых материалов? На этот вопрос, к сожалению, следуёт ответить отрицатель­но. Совокупность реологических свойств любого реального материала не является замкнутым множеством и по мере уг­лубления знаний о механическом поведении материала пред­ставляет собой расширяющуюся сферу характеристик. Следовательно, применение каждого отдельного прибора обосно­вывается целью исследования и абсолютно универсальных приборов принципиально не может существовать. Можно лишь сказать, что при постановке многоцелевых исследова­ний перспективными являются различные реометрические стенды, комплексы и лаборатории, автоматизированные в уп­равлении, записи и обработке данных.

Вторым принципиально важным общим вопросом реометрии является вопрос о существовании приборов и методов, позволяющих определить реологические свойства, абсолютно не зависящие от измерительной аппаратуры. На этот вопрос тоже следует ответить отрицательно, если принять за аксио­му, что любое воздействие на реальные материалы, а особен­но на такие сложные как пищевые, изменяет их реологиче­ские свойства, хотя и в различной степени. В то же время, хо­тя и не существуют приборы, дающие абсолютно безотноси­тельные свойства материалов, тем не менее можно выделить группу условно абсолютных приборов, теория которых доста­точно глубоко разработана и позволяет получать приборно-инвариантные реологические параметры материалов в трех смыслах:

1. Приборно-инвариантные реологические константы в смысле дисперсионного критерия, оценивающего неизменность измеряемых параметров материала при вариациях геометри­ческих, кинематических и динамических параметров прибора.

2. Инвариантные константы в смысле сравнительного критерия, оценивающего меру совпадения одноименных рео­логических констант, измеренных на принципиально различ­ных по конструкциям реометрах.

3. Инвариантные константы в смысле реодинамического критерия, оценивающего применимость измеренных на рео­метре констант при описании процессов течения в различных перерабатывающих машинах и устройствах.

Сравнительно хорошо удовлетворяющими названным кри­териям и наиболее распространенными в реометрии пищевых материалов реометрами следует признать ротационные и ка­пиллярные вискозиметры (например, РВ-8, реотест, Ml, АКВ-5, вискозиметр МТИПП и т. д.).

Очевидно, что при планировании и организации реометрических исследований большое значение имеет классифика­ция приборов и методов исследований. Рассмотрим некоторые системы классификаций. [8] делит реометры на три типа:

1. Приборы, на которых реализуется однородная дефор­мация. Например, машины для испытания твердых тел на рас­тяжение и сжатие.

2. Приборы ламинарного полуоднородного сдвига, обра­ботка данных на которых вследствие неоднородного поля де - формаций требует интегрирования или дифференцирования эмпирических результатов. Это, например, ротационные и. ка­пиллярные вискозиметры.

3. Приборы на которых реализуется ламинарное течение более сложного вида. Например, вискозиметры с падающим шариком.

[91 предлагает сгруппировать приборы и методы в две группы:

1. Интегральные методы и приборы, дающие показатели суммарного эффекта течения. Например, вискозиметры.

2. Дифференциальные методы и приборы, позволяющие определять деформации во времени в каждой точке среды. Например, методы с применением рентгеноскопии и наблю­дений на поверхности деформируемой среды.

В книге и др. [3] приборы разбиты на 4 группы по предназначению:

1.  Промышленные приборы для непрерывных измерений в потоке и автоматизации контроля и управления.

2.  Лабораторные приборы для массового технологического контроля.

3.  Приборы для углубленных измерений в промышленных лабораториях.

4.  Исследовательские приборы для научных целей.

Основательный обзор способов классификации объектив­ных методов измерения структуры и консистенции пищевых продуктов даны в работе [10].

Можно предложить еще систему классификации приборов в реологических исследованиях по функциональному принци­пу, которая представлена графически на рис. 22 и представ­ляется полезным дополнением к уже существующим системам.

§ 9. КАПИЛЛЯРНАЯ ВИСКОЗИМЕТРИЯ

Вискозиметры, в том числе и капиллярные, служат для оп­ределения вязкостных свойств материалов. Идея капиллярных вискозиметров заключается в том, что измеряя расход, пере­пад давлений, длину и диаметр капилляра, по которому течет материал, можно рассчитать меру сопротивления материала сдвиговому течению. Особенно проста эта задача для ньюто­новских жидкостей, ламинарное течение, которых в капилляре описывается известным уравнением Пуазейля. Последнее можно представить в виде:

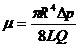(130)

где μ - коэффициент динамической вязкости,

R - радиус капилляра,

ΔР - перепад давления на длине капилляра,

L - длина капилляра,

Q - объемный расход материала через капилляр.

Схема течения в капилляре вискозиметра представлена на рис. 23.

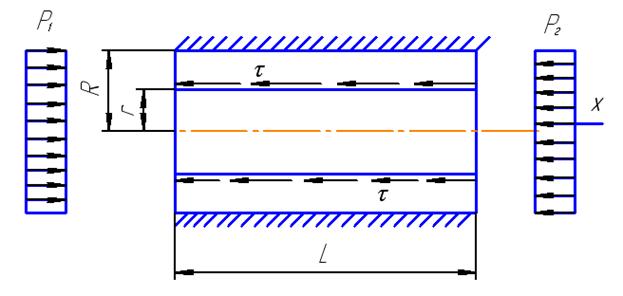
Рис. 23. Схема течения в капилляре вискозиметра

Выделив в жидкости цилиндрическое тело радиусом r, легко записать условие равновесия:

(131)

где τ - касательные напряжения на поверхности цилиндра

радиусом r.

Из уравнения (131), учитывая обозначение , получим

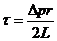(132)

(133)

где τmax и τc — максимальные касательные напряжения на стенке капилляра.

Очевидно, касательные напряжения по радиусу распреде­ляются по линейному закону и равны нулю при r = 0. Заметим, что формулы (132) и (133) справедливы также для неньютоновских жидкостей, поскольку уравнение (131) не налагает на это ограничений.

Вспомнив вид реологического закона Ньютона, и записав его для точки на стенке капилляра:

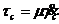(134)

где γc и τс — скорость и напряжение сдвига на стенке капил­ляра, получим из совместного решения уравне­ний (130), (133) и (134) формулу вида:

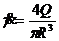(135)

Кстати, величины τс и ус в литературе иногда называются консистентными переменными Рейнера Р и V, которые опре­деляются выражениями вида:

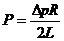; (136)

Если для ньютоновских жидкостей скорость сдвига на стенке капилляра определяется формулой (135), полученной с использованием выражения (130), то для неньютоновских жидкостей формула (135) несправедлива из-за нарушения закона Пуазейля (130) при течении этих жидкостей в капил­ляре. Для определения скорости сдвига неньютоновскнх жид­костей на стенке капилляра рассмотрим вначале общую за­дачу вычисления расхода.

Пусть реологический закон неньютоновской жидкости за­писан в общем виде

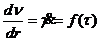(137)

где v — скорость течения жидкости вдоль капилляра. Из формул (132) и (133) получим

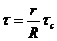(138)

и задача выяснения распределения скоростей течения сводит­ся к интегрированию:

*

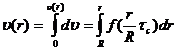* (139)

Интегрируя функцию υ(r) по площади поперечного сече­ния капилляра, используя интегрирование по частям и про­изведя замену переменных r на τ получим

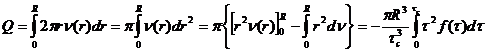(140)

Знак минус перед интегралом в выражении (140) можно опустить, поскольку его появление объясняется тем, что рас­ход Q является положительной величиной, а величина Δр, ко­торая появляется в формуле расхода (140) после интегриро­вания и соответствующих подстановок меньше нуля из-за не­равенства p2<p1. Естественно, при этом в формулу расхода подставляется абсолютное значение /Δр/.

Выражение (140) позволяет записать уравнение

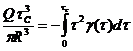(141)

Дифференцируя (141) по τс получим

(142)

или

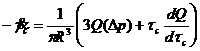(143)

Выражение (143) называется формулой Рабиновича-Муни и лежит в основе обработки данных капиллярной вискози­метрии неньютоновских жидкостей. Возможны некоторые модификации формулы (143):

(144)

(145)

Теперь очевидно, как следует обрабатывать данные вискозиметрирования неньютоновских жидкостей. Следуя, на­пример, формуле (144), после получения технической кривой течения в координатах Q и Δр, выбирают определенное значе­ние Δpi затем рассчитывают величину τc1 по формуле (133) и, произведя, допустим, графическое дифференцирование функции Q(Δp) в точке Δр1, получают величину и определяют γc1 по формуле (144). Множество γc1 и τc1, где индексы стенки теперь можно опустить, определяет кривую течения τ = f(γ), для которой остается подобрать пригодную интерполяционную формулу из числа распространенных рео­логических законов течения. Конечно, все эти операции не обязательно производить таким наглядным образом по точ­кам технической кривой Q(Δp). Последнюю можно сразу обработать с получением эмпирической формулы и все после­дующие операции выполнить аналитически.

Покажем, что игнорирование формулы (144) может при­вести к существенным ошибкам. Действительно, пусть стоит задача определения эффективной вязкости т)3ф, например, степенной жидкости (Оствальда-де-Вале) по формуле вида

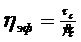(146)

Для степенной жидкости с реологическим законом вида

(147)

где К —коэффициент консистенции,

п — индекс течения.

По формуле (140) можно получить аналог формулы Пуа-зейля:

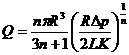(148)

Из формулы (144) и (148) получим

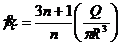(149)

Тогда правильное значение эффективной вязкости опреде­ляет формула

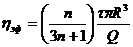(150)

Ошибочное значение ηэф получим, если полагать, что ско­рость сдвига на стенке капилляра для степенной жидкости можно рассчитать по формуле (135). Тогда из формул (135) и (146)

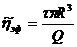(151)

и величину ошибки δ при, например, n = 0,5 легко рассчитать

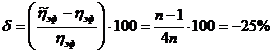(152)

Необходимо сделать еще несколько практически важных замечаний.

1.  При вискозиметрировании следует обеспечивать лами­нарный режим течения.

2.  Из данных следует исключать концевые эффекты, на­ пример, методом двух капилляров. Иначе говоря, строятся две технические кривые течения для двух капилляров разной дли­ны L1 и L2 с одинаковой геометрией входа и выхода, а все изложенные выше расчеты производят по технической кривой Q(Δp), построенной по аргументу Δр как перепаду давлений на разности длин L = L2 – L1.

3.  Необходимо проверить отсутствие эффекта пристенного проскальзывания, например, по совпадению кривых течения в консистентных переменных для капилляров различного диа­метра.

4.  При измерениях расхода Q весовым способом нужно помнить, что многие пищевые материалы имеют свойство уп­лотняться под давлением. Этот вопрос требует специальных исследований материала в условиях всестороннего сжатия.

Рассмотрим обработку данных вискозиметрирования в слу­чае проскальзывания материала по стенке капилляра. Пола­гая, что эффективная скорость проскальзывания и зависит от касательных напряжений τс на стенке капилляра, перепишем формулу (139) в новом виде:

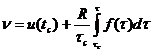(153)

Тогда формула (140) приобретет вид:

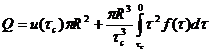(154)

или

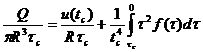(155)

введем обозначения:

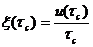(156)

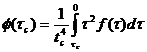(157)

где эффективный коэффициент скольжения по Олдройду

Тогда выражение (155) примет вид

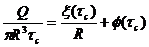(158)

Эффективный коэффициент скольжения можно опреде­лить из серии опытов с трубами различного диаметра. Дейст­вительно, построив опытные данные в координатах Q/πR3τc и τс, получим серию кривых течения. Заметим, что эти кривые совпадают в случае отсутствия проскальзывания, что следует из условия u(τс) = 0, уравнений (158), (145) и (137). Иначе говоря, кривые течения в консистентных переменных для раз­личных капилляров при отсутствии проскальзывания совпа­дают. Действительно, переписав формулу (137) в виде:

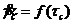(159)

и подставив в выражение (159) величину ус из формулы (145), получим

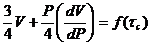(160)

Поскольку формулы (159) и (160) отражают независя­щие от геометрии прибора реологические свойства материа­ла, а в формулу (160) входят только консистентные перемен­ные, то связи между конситентными переменными инвари­антны по отношению к геометрии прибора. Кстати, инвари­антность кривых течения в консистентных переменных можно использовать для расчета трубопроводов различной длины и радиуса, если испытаниями получена кривая течения в кон­систентных переменных для одной трубы фиксированной дли­ны и радиуса.

Проскальзывание отмеченную инвариантность нарушает — формула (145) выведена при условии отсутствия проскаль­зывания.

По графикам (рис. 24) строим графики в координатах

(рис. 25) при выбранных значениях τc. Эти графики будут прямыми, которые имеют тангенсы углов наклона, равные эффективным коэффициентам скольжения, а ординаты при равные функции .

Это позволяет построить искомую функцию , а также функцию . Последняя дает возможность определить ско­рость сдвига . Действительно, дифференцируя выражение (157) по , получим:

(161)

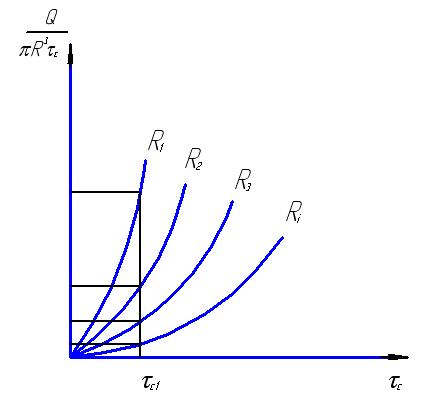
Рис.24. Кривые течения, полученные в вискозиметре с капиллярами разного диаметра

Следовательно, проскальзывание по стенке не делает не­возможным получение реологического закона течения мате­риала, хотя сильно усложняет обработку данных вискози­метрии. Определенные опасности заключаются в нарушении ламинарности потока, поскольку турбулизация дает характер­ную для проскальзывания картину расслоения кривых тече­ния (рис. 24) и может привести к ложному истолкованию ре­зультатов опытов.

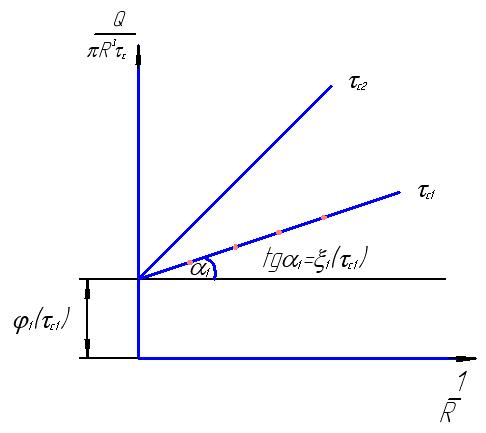
Рис. 25. Графики для определения коэффициента скольжения

§ 10. РОТАЦИОННАЯ ВИСКОЗИМЕТРИЯ

Ротационные вискозиметры в пищевой реометрии распро­странены, пожалуй, даже больше, чем капиллярные. Идея ро­тационных вискозиметров заключается в том, что меру сопро­тивления сдвиговому течению можно определить, измеряя вращающий момент и угловую скорость при относительном вращении коаксиальных цилиндров или конусов (реже тел других форм), в зазоре между которыми находится вязкая жидкость.

Схема течения в ротационном вискозиметре с коаксиаль­ными цилиндрами изображена на рис. 26, где для определен­ности пусть внутренний цилиндр неподвижен, а наружный вращается с угловой скоростью ω.

В случае вискозиметрирования ньютоновских жидкостей коэффициент динамической вязкости можно определить по формуле Маргулеса, которая для ротационных вискозиметров выполняет ту же роль, что формула Пуазейля для капилляр­ных вискозиметров:

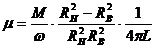(162)

где М — крутящий момент, приложенный к внешнему ци­линдру,

Rh, Rb — радиусы наружного и внутреннего цилиндров соот­ветственно,

L — высота слоя жидкости между цилиндрами,

ω — угловая скорость наружного цилиндра.

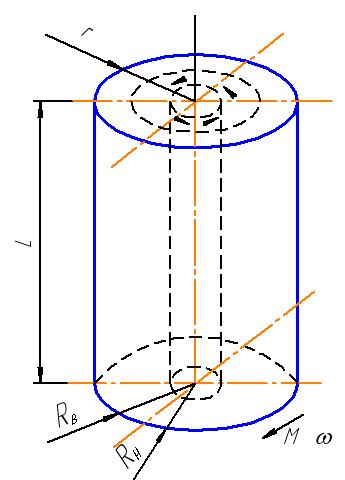
Рис.26. Схема течения в ротационном вискозиметре с коаксиальными цилиндрами.

Для цилиндрического слоя радиуса r можно составить уравнение равновесия в виде суммы моментов относительно оси цилиндров:

(163)

или

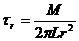(164)

где тг — касательные напряжения в слое жидкости на ра­диусе r.

Решая совместно уравнения (162), (164) с учетом ньюто­новского закона течения получим:

(165)

где — скорость сдвига в слое жидкости на радиусе r.

Формулы (164) и (165) позволяют записать:

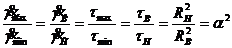(166)

где - скорость сдвига в жидкости соответственно на стенках внутреннего и наружного цилиндров,

- касательные напряжения на стенках внутреннего и наружного цилиндров,

α - геометрический симплекс.

Заметим, что выражение (166) в части касательных на­пряжений справедливо также для неньютоновских жидкостей, .а в части скоростей сдвига — только для ньютоновских жид­костей.

Попытаемся решить задачу определения скоростей сдви­га в общем случае, как это было сделано для капиллярного вискозиметра.

По связи между угловыми и линейными скоростями за­пишем:

(167)

и по определению скорости сдвига

(168)

где νr, ωr - линейная и угловая скорости слоя радиусом r. Располагая законом течения (пока неизвестным) вида

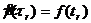(169)

из выражения (168) получим

(170)

Произведем замену переменной г правой части выраже­ния (170), пользуясь аналогичным равенством (166) форму­ле вида:

(171)

И очевидным тогда

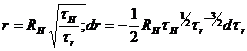(172)

Замена переменных и интегрирование дает выражение вида:

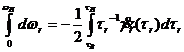(173)

или

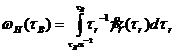(174)

По аналогии с теорией капиллярных вискозиметров диф­ференцируем (174) по верхнему пределу интеграла:

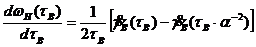(175)

Вид функционального уравнения (175) не позволяет даль­ше развить прямую аналогию с теорией капиллярных вис­козиметров, поскольку уравнение (175) не разрешается так. просто относительно функции , как это имело место при получении уравнения Рабиновича.

Решение возникшей задачи было дано [1] в 1953 году и может быть представлено в виде:

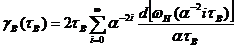(176)

Очевидно, что нахождение скоростей сдвига на стенке внутреннего цилиндра при определенном значении напряже­ний сдвига τB также гораздо более сложная задача, чем ана­логичная задача для капиллярных вискозиметров. Это при­водит в практике к стремлению использовать вместо формулы (176) различные приближенные, более простые формулы. При использовании этих формул следует всегда оценить их точность в данном конкретном случае по отношению к фор­муле (176), иначе возможны грубые ошибки.

Рассмотрим задачу оценки погрешности по эффективной вязкости при вискозиметрировании степенной жидкости и подсчетах скоростей сдвига по точной формуле (176) и приближенной (165), как это было сделано в случае капиллярного вискозиметра. Эффективная вязкость по приближенной фор­муле будет иметь вид:

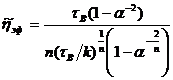(177)

а по точной:

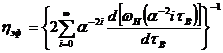(178)

Опуская выкладки, получим:

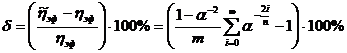(179)

Пусть n = α-1 = 0,5 тогда δ = 60%

Задача вычислений по формуле (176) достаточно просто решается графически, поэтому ее следует гораздо шире ис­пользовать в обработке данных ротационной вискозиметрии, чем распространенные приближенные формулы.

Наиболее часто используют приближенные формулы двух видов:

1.  Непосредственно вытекающую из формулы Маргулеса:

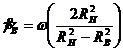(180)

2. Получаемую из соображений малости зазора, при котором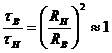

(181)

Анализ некоторых других формул и развернутое изложе­ние теории ротационных вискозиметров можно найти в фун­даментальной книге , и Лео­нова А. И. «Ротационные приборы».

Заметим в заключении, что при ротационном вискозиметрировании необходимо, также как при капиллярном, сохра­нять ламинарный режим течения, исключать концевые эффек­ты методом двух пар разной длины цилиндров (либо же пре­небрегать этими эффектами при условии L››RH), проверять отсутствие эффекта пристенного проскальзывания (например, сравнением данных, полученных с помощью гладких и риф­леных цилиндров, или цилиндров различных радиусов и зазоров). В отличие от капиллярных вискозиметров, здесь проб­лемы уплотнения массы из-за давления не возникает, однако могут возникнуть проблемы, связанные с механическим разо­гревом массы в зазоре. Особенно внимательно нужно отно­ситься к выбору величины зазора при вискозиметрировании пищевых дисперсных систем с большими твердыми включе­ниями, чтобы не превратить вискозиметр в процессе измере­ния в мельницу.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7