величиной не постоянной, зависящей от величины приложенных напряжений или скоростей сдвига.
У большинства перерабатываемых пищевых масс этот коэффициент уменьшается с ростом напряжений или скоростей сдвига. Объясняется это тем, что пищевые массы - это, как правило, структурированные системы, то есть системы, имеющие определенную макро - и микроструктуру. Например, густая конфетная масса, пралине - это какао-масло, в котором имеются измельченные, неправильной формы кусочки жареного ореха и кристаллики сахара. Когда массу приготовили - все ее компоненты как-то взаимно расположились, где-то соединились. Начинаем прикладывать напряжения - начинается сдвиг слоев друг относительно друга, с каким - то сопротивлением, определяемым организовавшейся структурой. Чем больше прикладываемые напряжения и скорости сдвига, тем в больших местах происходит разрыв связей компонентов структуры, неправильной формы частицы все больше ориентируются по потоку. За счет этого происходит уменьшение сопротивление смещению слоев друг относительно друга, то есть падает вязкость, определяемая коэффициентом вязкости, который, следуя ньютоновскому понятию вязкости, называется теперь эффективной вязкостью μ эф
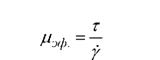
Итак, если у ньютоновской идеальной вязкости жидкости коэффициент вязкости постоянен, то у реальных пищевых жидкостей коэффициент эффективной вязкости не есть константа.
"Аномальное" вязкое течение пищевых масс наиболее часто встречается. И лишь очень немногие реальные жидкости подчиняются "нормальному" ньютоновскому закону.
Оствальд в 30-е годы ввел понятие структурированной системы, для которой можно наблюдать закон изменения эффективной вязкости, в соответствии с рисунком 4.
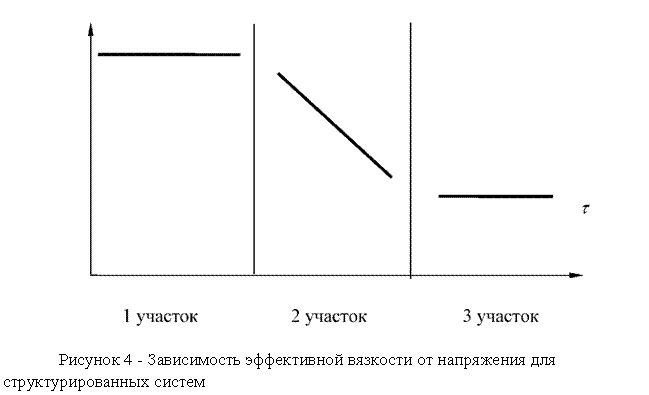
У реальных пищевых масс, структурированных систем, можно наблюдать три участка: участок 1 - малые сдвиговые напряжения, практически неразрушенная структура и соответствующая ей большая, носящая ньютоновский μ эф характер (константа) вязкость; участок 2 - растут напряжения, все больше
разрушается структура, все меньшее значение приобретает эффективная вязкость; участок 3 - практически разрушена структура, вновь начинается ньютоновское течение, но уже с наименьшим значением вязкости.
Механические модели, отражающие элементарные реологические свойства
В реологии различные материалы представляются механическими моделями, составленными из простых идеализированных тел. Механические модели позволяют представить, как ведет себя тот, или иной, материал под нагрузкой. По этим механическим моделям составляют математические уравнения зависимостей различных параметров: касательных τ и нормальных σ напряжений, угловых γ и линейных ε деформаций, скоростей изменения этих деформаций
(![]() и
и ![]() ), времени t. Зависимости параметров между собой часто изображают на
), времени t. Зависимости параметров между собой часто изображают на
графиках.
При составлении механических моделей исходят из положения, что деформация сложного тела является результатом наложения деформаций элементарных механических моделей идеализированных тел, отражающих основные реологические свойства. К основным реологическим свойствам, которые наблюдаются у реальных тел, относятся: вязкость, упругость и пластичность.
Моделью упругого твердого тела является пружина, или тело Гука, в соответствии с рисунком 5.
где G - модуль сдвига. Для растяжения-сжатия |
Соответствующей математической моделью является реологическое уравнение гуковского твердого тела для простого сдвига
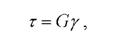
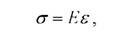
где E - модуль упругости.
Реологической константой является модуль сдвига G. Напряжение, воз-никаемое в этом теле, прямопропорционально деформации.
Механической моделью вязкой жидкости является гидравлический поршень, в соответствии с рисунком 6, или тело Ньютона.
Соответствующей математической моделью является реологическое уравнение состояния ньютоновского тела для простого сдвига
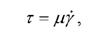
где μ - вязкость.
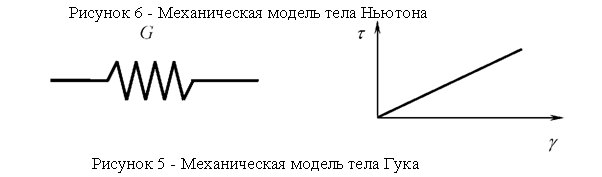 |
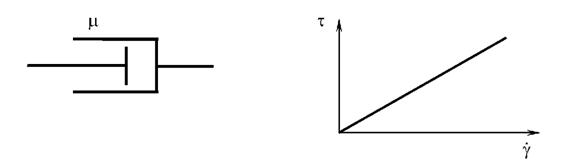
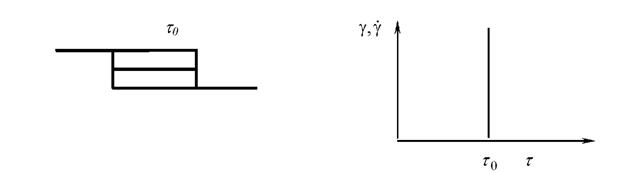
Рисунок 7 - Механическая модель тела Сен-Венана
Реологической константой является вязкость μ. Напряжение, возникающее в этом теле, прямопропорционально скорости сдвига.
Модель идеальнопластичного тела изображается в виде пары трения, в соответствии с рисунком 7, и определяется как тело Сен-Венана.
Оно неподатливо (ε = 0;![]() = 0;γ = 0;
= 0;γ = 0;![]() = 0) при нагружении ниже предела текучести (σ <Θ0 или τ <τ0), а после его превышения (σ
= 0) при нагружении ниже предела текучести (σ <Θ0 или τ <τ0), а после его превышения (σ![]() Θ0 или τ
Θ0 или τ ![]() τ0), неограниченно деформируется (ε
τ0), неограниченно деформируется (ε ![]()
![]() ;
;![]()
![]() ;γ
;γ![]() ;
;![]()
![]() ), при этом в теле возникают напряжения равные пределу текучести (σ = Θ0;τ = τ0). Предел текучести т0 является реологической константой элемента пластичности.
), при этом в теле возникают напряжения равные пределу текучести (σ = Θ0;τ = τ0). Предел текучести т0 является реологической константой элемента пластичности.
Модель твердого тела, или тело Ренкина, изображается как пара сцепленных пластин, в соответствии с рисунком 8. Реологическая константа данного элемента - предел прочности τВ или σВ. Если при нагружении достичь предела прочности (τ = τВ), сцепленные пластины необратимо разъединяются (![]() ;
;![]() ). При нагружении менее предела прочности (τ<τВ) тело неподатливо (
). При нагружении менее предела прочности (τ<τВ) тело неподатливо (![]() = 0;
= 0; ![]() = 0).
= 0).
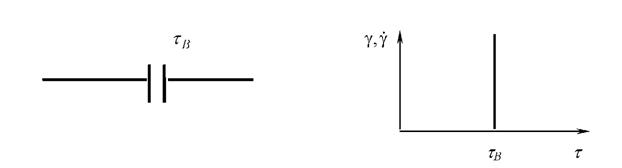
Рисунок 8 - Механическая модель тела Ренкина
Модель твердого тела, в соответствии с рисунком 9, учитывающая необратимую мгновенную деформацию, была введена Пелегом.
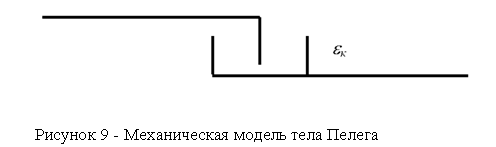 |
При нагружении тело Пелега сначала деформируется в пределах 0
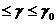 , а после достижения контакта ведет себя как жесткое тело.
, а после достижения контакта ведет себя как жесткое тело.
ОСНОВЫ ЛИНЕЙНОЙ ВЯЗКОУПРУГОСТИ
Мы уже знакомы с примерами простого поведения материалов при нагружении. Это описанные ранее идеальные тела Гука, Ньютона и Сен-Венана, поведение которых при нагружении символизирует основные простейшие элементы свойств материалов: упругость, вязкость и пластичность.
Более того, мы уже знаем о том, что реальные материалы, как правило, обладают сложным комплексом свойств, являющихся определенной комбинацией перечисленных выше трех простейших — упругости, вязкости и пластичности.
Прежде чем перейти к составлению новых моделей, символизирующих поведение реальных пищевых материалов, имеет смысл разработать аппарат, в том числе и математический, описывающий идеальные тела, наделенные определенными сочетаниями трех простейших свойств. Выше были рассмотрены первые примеры этих более сложных идеальных тел. Тело Бингама, например, обладало сочетанием вязких и пластических свойств, т. е. сочетало в себе свойства тел Гука и Сен-Венана.
Теперь нам предстоит более подробно обсудить большую группу моделей идеальных тел, обладающих сочетанием вязких и упругих свойств. Математическая модель этих тел будет представлять собой уравнение, связывающее напряжения, деформации и их первые, и более высокие производные. Для простоты рассмотрим лишь варианты линейной зависимости такого рода.
Начнем с введенного еще в 1890 г. Уильямом Томсоном (он же лорд Кельвин) понятия вязкости твердого тела.
Тело Кельвина
(иногда его же именуют телом Фойгта)
Механическая модель тела Кельвина представляет собой параллельно соединенные элементы Гука и Ньютона (рис. 6)
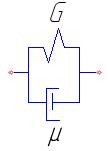
Рис. 6. Механическая модель тела Кельвина.
с реологическими характеристиками G (модуль упругости) и μ (ньютоновская вязкость). Для написания математической модели тела Кельвина используем то обстоятельство, что при параллельном соединении элементов деформация сложного тела γк равна деформации каждого элемента, а напряжение суммарного элемента τк равно сумме напряжений в отдельных элементах τг и τн. На основании этого мы имеем систему уравнений (59):
![]() (59)
(59)
Воспользуемся записанными ранее математическими моделями для элементов Гука (Г) и Ньютона (Н)
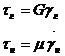 (60)
(60)
Рассмотрев совместно (59) и (60), получим окончательно математическую модель тела Кельвина в таком виде
![]() (61)
(61)
Исключив деформации и напряжения с индексами «Г» и «Н» (помня, что в данном случае ![]() ), будем впредь окончательно записывать математические модели вновь полученных тел без соответствующих индексов (сейчас без индекса «К»). Т. о. окончательно уравнение тела Кельвина будем записывать так:
), будем впредь окончательно записывать математические модели вновь полученных тел без соответствующих индексов (сейчас без индекса «К»). Т. о. окончательно уравнение тела Кельвина будем записывать так:
![]() (62)
(62)
Как мы говорили, Кельвин ввел это идеальное тело для того, чтобы иметь возможность показать свойство вязкого течения для «твердого тела». Это явление, характеризующееся самопроизвольным развитием деформацией при постоянном значении приложенных напряжений, имеет специальное название — ползучесть.
Рассмотрим математическое описание ползучести, т. е. развития деформаций во времени γ=γ(t) при постоянном напряжении τ = τс = const. Уравнение тела Кельвина в этому случае превращается в дифференциальное
уравнение вида:
![]() (63)
(63)
где «а» и «b» — постоянные коэффициенты, равные в нашем случае
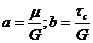 (64)
(64)
Переменная у имеет значения деформации, дифференцирование ведется по времени.
Из курса высшей математики известно решение уравнения (63), имеющее вид:
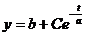 (65)
(65)
где произвольная постоянная интегрирования С должна быть определена из начальных условий.
Итак, окончательно для нашего случая решение имеет вид:
![]() (66)
(66)
Запишем в качестве начальных условий следующее:
при t=0, γ=γ0=0. (67)
справедливость чего очевидна, т. к. уже рассмотрение механической модели тела Кельвина показывает, что ввиду параллельности соединения элементов Гука и Ньютона (что необходимо для получения тела Кельвина) и ввиду отсутствия мгновенной (сразу после приложения напряжения) деформа ции в ньютоновском элементе, мгновенная деформация тела Кельвина отсутствует.
Таким образом нам удается определить значение произвольной постоянной
![]() (68)
(68)
Окончательно, интересующее нас решение выглядит так, как это показано на рис. 7.
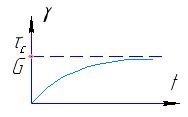
Рис. 7. Кривая кинетики деформации тела Кельвина
При стремлении t → ∞ деформация γ ассимптотически приближается к значению τс/G. Вспомним, что для тела Гука, упругие деформации которого определяются соотношением:
![]() (69)
(69)
при приложении напряжения τ = τc, имела бы место мгновенно возникающая деформация, равная γ=τc/G, т. е. деформация как раз равная тому значению, которого достигнет, в конце концов, деформация в теле Кельвина при действии на него напряжения τc. Этим объясняется часто употребляемое название одного из характерных свойств тела Кельвина — запаздывающая упругость (т. е. не мгновенная, как в теле Гука, но достигающая того же, что в теле Гука значения). Чем большее значение будет иметь коэффициент G/μ, тем резче будет возрастать деформация ползучести.
Тело Максвелла
Рассмотрим другой случай сочетания упругих и вязких свойств. В 1920 году Гесс наблюдал необычное поведение вязкой жидкости 1,5% раствор крахмала, внешне вполне напоминающий вязкую жидкость, помещался в сосуд. Сосуд раскручивался и резко останавливался. Жидкость продолжала вращаться со все уменьшающейся, в силу наличия вязкости, скоростью. Но если в случае затухания вращения такой же вязкости, но другой жидкости — раствора глицерина с водой — жидкость, все более медленно вращаясь, наконец, останавливалась, то 1,5% раствор крахмала вел себя не так. Вращение (допустим по часовой стрелке) постепенно затухало и..., остановившись, вновь начиналось самопроизвольно, но уже в обратном (против часовой стрелки) направлении. Затем вновь остановка и вращение по часовой стрелке. Иными словами, вязкая жидкость обнаруживала наличие упругих свойств (вспомним, как затухают упругие колебания пружины — тела Гука).
Для описания такого поведения реального материала в качестве первого приближения можно взять модель тела Максвелла, в механическом варианте которого последовательно соединены элементы Гука и Ньютона (рис. 8).
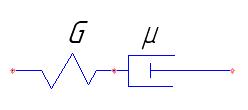
Рис. 8. Механическая модель тела Максвелла.
В самом деле, такая модель «течет» как жидкость. Она же обладает упругими свойствами (например, при приложении мгновенных напряжений, мгновенно деформируется как упругое тело на какую-то величину). После мгновенной, упругой деформации продолжается вязкое течение. Кстати, если на механической модели «проиграть» вариант приложения напряжения и фиксации возникших деформаций, то станет видно (рис. 9), что со временем приложенные напряжения будут уменьшаться и исчезнут вообще.
Такое явление самопроизвольного уменьшения напряжений при постоянной деформации носит название релаксации напряжений. Получим уравнение тела Максвелла и найдем решение этого уравнения, характеризующее релаксацию напряжений.
Для последовательно соединенных в тело Максвелла элементов Гука и Ньютона характерно равенство напряжений
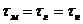 (70)
(70)
и суммирование деформаций, т. е.
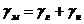 (71)
(71)
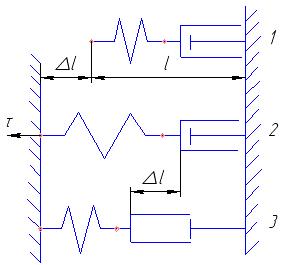
Рис. 9. Механическая интерпретация процесса релаксации напряжений.
1. Нагрузки нет;
2. Приложили напряжение и зафиксировали деформацию;
3. Напряжение исчезло (релаксировало).
Разрешив (60) относительно деформации ![]() и скорости деформации
и скорости деформации ![]() , получим
, получим
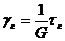 (72)
(72)
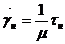 (73)
(73)
Продифференцировав левые и правые стороны (71) и (72) и рассмотрев их совместно с (70) и (73), получим математическую модель тела Максвелла (опустив, как это было у тела Кельвина, индексы)
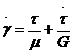 (74)
(74)
Для изучения релаксации напряжений при постоянной деформации это уравнение удобно переписать в следующем виде:
![]() (75)
(75)
Итак, пусть γ = γc = const. Тогда γ =0 и (75) перейдет в
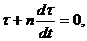 (76)
(76)
где ![]() (подробнее об этом коэффициенте несколько позже).
(подробнее об этом коэффициенте несколько позже).
Проведем разделение переменных τ и t
![]() (77)
(77)
![]() (78)
(78)
Проинтегрируем левую и правую часть (78) и получим
![]() (79)
(79)
где С — произвольная постоянная интегрирования.
Сделаем некоторые преобразования (79)
![]() (80)
(80)
![]() (81)
(81)
Тогда
![]() (82)
(82)
Обозначив в (82) постоянную величину ![]() новой постоянной С, получим
новой постоянной С, получим
![]() (83)
(83)
Для получения значения произвольной постоянной из (83) вспомним, что в начальный момент мы приложили напряжение τ=τ0 т. е. при t=0, τ = τ0.
Тогда из (83) следует, что С = τ0 и окончательно решение имеет вид
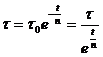 (84)
(84)
Изобразим это решение графически при разных значениях n (см. рис. 10).
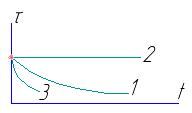
Рис. 10. График релаксации напряжений.
Случай 1 рис. 10 графически показывает релаксацию (самопроизвольное уменьшение по экспоненте) напряжений во времени.
При t→ ∞, τ→ 0
Коэффициент n, входящий в уравнение тела Максвелла имеет размерность времени

и называется коэффициентом времени релаксации. При n→ ∞ релаксации напряжений не происходит (случай 2 рис, 10), при n→ 0 происходит практически мгновенная релаксация напряжений (случай 3 рис. 10).
Для тела Максвелла, как это следует из (84), коэффициент времени релаксации численно равен времени, в течение которого напряжение в процессе релаксации уменьшается в е = 2,73 раза по сравнению с первоначальным его значением.
Проанализируем поведение тела Максвелла в различных случаях его нагружения и деформирования.
Как, например, развиваются деформации в теле Максвелла при действии на него постоянного напряжения τ= τ0= const. Т. к. при этом τ = 0, то (75) превращается в
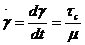 (85)
(85)
Откуда
![]() (86)
(86)
Интегрируем левую и правую часть и получаем
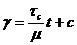 (87)
(87)
Для нахождения произвольной постоянной С запишем, что при t = 0, γ=γ0, откуда следует, что произвольная постоянная равна деформации, мгновенно возникающей в момент приложения напряжения. Окончательно γ=γ(t) имеет вид
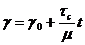 (88)
(88)
т. е. деформация в этом случае линейно возрастает.
Другой случай. Как ведут себя напряжения τ в теле Максвелла, если его деформировать с постоянной скоростью, т. е. Если
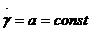
В этом случае (75) превращается в
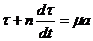 (89)
(89)
т. е. имеет вид уравнения (63), решением для которого будет (65). Для нашего случая, таким образом, решение будет
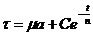 (90)
(90)
Для определения произвольной постоянной С зададим начальные условия. Мгновенно приложили τ =τ0 и затем начали деформировать с постоянной скоростью ![]() Т. о при t = 0, τ=τ0; тогда из (90) следует, что
Т. о при t = 0, τ=τ0; тогда из (90) следует, что
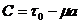 (91)
(91)
и окончательно τ=τ(t) будет иметь следующий вид
![]() (92)
(92)
При условии, что ![]() будем иметь деформирование с неменяющимися напряжениями, т. е. случай 1, рис. 11, если
будем иметь деформирование с неменяющимися напряжениями, т. е. случай 1, рис. 11, если
a > ![]() — случай 2, если
— случай 2, если
a < ![]() — случай 3.
— случай 3.
§ 7. ОСНОВНОЙ УПРОЩЕННЫЙ ЗАКОН ВЯЗКО-УПРУГОГО ДЕФОРМИРОВАНИЯ
Рассмотренные модели тел Кельвина и Максвелла, учитывающие наличие определенного сочетания упруго-вязких свойств, не удовлетворяют практику, ибо описывают сочетания свойств, имеющие место лишь в ряде случаев поведения реальных тел при деформировании.
Следующим шагом на пути приближения свойств идеального тела к проявляемым реальными материалами является трехпараметрическая (составленная из 3-х элементов — двух гуковых и одного ньютоновского) модель, один из вариантов которой представляет собой последовательно соединенные элементы Кельвина и Гука (рис. 12).
Рис. 12. Механическая модель обобщенного линейного тела.
Модель эта имеет много наименований (например, тело Максвелла-Томсона), однако чаще ее именуют моделью обобщенного линейного тела (ОЛТ).
Один из вариантов реологического уравнения (математической модели) ОЛТ записывается в следующем виде:
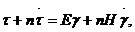 (93)
(93)
где: коэффициенты n, Е, Н, являющиеся реологическими характеристиками ОЛТ, называются так: n — коэффициент времени релаксации; H — условно-мгновенный модуль; Е — длительный модуль.
После того, как мы сами получим реологическое уравнение ОЛТ на основе анализа поведения его механической модели, нам станет ясно, почему эти коэффициенты так названы.
Итак, попробуем получить математическую модель ОЛТ так, как мы это делали в случае тел Кельвина и Максвелла.
Можно начать запись необходимых уравнений со следующего:
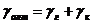 (94)
(94)
затем помня, что в ньютоновском элементе мы будем иметь дело с ![]() , а не с γ, продифференцировать (94)
, а не с γ, продифференцировать (94)
 (95)
(95)
Затем на основе закона Гука расшифровать
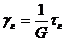
и т. д., и т. п.
Если в случае тел Кельвина и Максвелла это был технически довольно простой путь, то уже для ОЛТ он весьма длинен. А ведь будут и более сложные модели.
Имея это ввиду, целесообразно воспользоваться распространенным символическим методом построения математической модели по имеющейся механической.
Мы не будем доказывать справедливость этого метода, а проверив его правильность на уже известных математических моделях, используем его для построения упруго-вязкой модели практически любой сложности.
Итак, перечислим основные правила использования символического метода. Вводится символ D, означающий операцию дифференцирования, распространяющуюся на элемент, с которым соседствует символ D. Все операции с этим символом производятся по законам алгебры. И упругие и вязкие элементы считаются упругими, но «модуль упругости вязкого элемента» получают умножением символа D на коэффициент вязкости μ. Вводится понятие жесткости модели, обозначаемой G (D), под которой понимают то, что в простом законе Гука является модулем, т. е. считают для данной модели
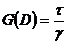 (96)
(96)
Жесткость G параллельно соединенных гуковских элементов G1 и G2 считают равной сумме этих жесткостей
G=G1+G2 (97)
Жесткость последовательно соединенных элементов G1 и G2 получают по следующему выражению
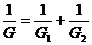 (98)
(98)
Для примера покажем справедливость выражения (97). Для первого упругого элемента (рис. 13) справедливо выражение закона Гука
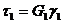 (99)
(99)
Для второго —
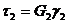 (100)
(100)
Для элемента, состоящего из двух параллельно соединенных элементов, справедливо следующее: общая деформация γ равна деформации каждого элемента, т. е.
![]() (101)
(101)
общее напряжение τ является суммой составляющих:
![]() (102)
(102)
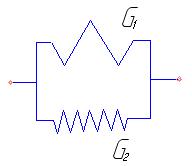
Рис. 13. Параллельное соединение двух элементов Гука.
тогда
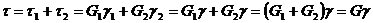 (103)
(103)
где G = G1 + G2 — жесткость общего элемента.
Аналогично можно показать и справедливость выражения (98).
Вот почти все, что нужно для работы с символическим методом построения математических моделей вязко-упругого поведения.
Применим этот метод для получения математической модели тела Максвелла, представляющей (с учетом высказанных выше правил) два последовательно соединенных упругих элемента G' и G" (рис. 14), жесткости которых соответственно G' = G; G" = Dμ.
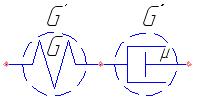
Рис. 14. Модель тела Максвелла.
Суммарную жесткость тела Максвелла мы будем находить, пользуясь выражением (98), поэтому нам понадобится не выражение 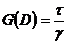 , а оно же, но разрешенное относительно
, а оно же, но разрешенное относительно ![]() , т. е.
, т. е.
![]() (103)
(103)
Итак, делаем окончательный вывод реологического уравнения тела Максвелла символическим методом.
![]() (104)
(104)
или с учетом (103):
![]() (105)
(105)
Проведя алгебраические преобразования, получим:
![]() (106)
(106)
или далее
![]() (107)
(107)
Переставив множители и разделив все на G, получим
![]() (108)
(108)
Теперь, вспомнив, что оператор D означает дифференцирование, применим его в одном случае для γ, а в другом — для т получим реологическое уравнение тела Максвелла (75), как это было сделано ранее
![]() (109)
(109)
Применим теперь этот опробованный способ для получения математической модели ОЛТ, которое рассмотрим как последовательно соединенные два упругих элемента G' и G" (рис. 15).
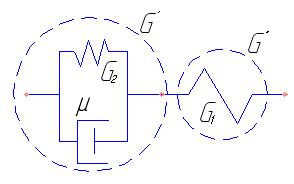
Рис. 15. Модель обобщенного линейного тела.
В свою очередь, элемент G' рассмотрим как два параллельно соединенных элемента с жесткостями G2 и Dμ.
Итак, запишем
![]() (110)
(110) ![]() На основе указанных выше правил
На основе указанных выше правил
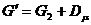 (111)
(111)
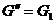 (112)
(112)
Таким образом
![]() (113)
(113)
что после алгебраических преобразований дает
![]() (114)
(114)
и, учитывая, что ![]() , получим возможность записать
, получим возможность записать
![]() (115)
(115)
Проведем дальнейшие алгебраические преобразования
![]() (116)
(116)
![]() (117)
(117)
Для окончательного получения математической модели в виде, показанном в начале параграфа, разделим все на (G1+G2) и проведем дифференцирование в тех местах, где есть символ D.
![]() (118)
(118)
Используя ранее введенные обозначения, вспомним, что 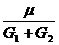 по размерности являющееся временем, есть не что иное, как коэффициент «времени релаксации»;
по размерности являющееся временем, есть не что иное, как коэффициент «времени релаксации»; ![]() по размерности может служить модулем «Е», a
по размерности может служить модулем «Е», a ![]() является произведением модуля «Н» на коэффициент времени релаксации «n».
является произведением модуля «Н» на коэффициент времени релаксации «n».
Для обоснования названия полученных модулей рассмотрим, на основе анализа механической модели, хотя бы качественно, кривую кинетики деформации, т. е. кривую вида γ=γ(t), для ОЛТ. Кстати, то же самое можно сделать более строго, проанализировав решение уравнения (118) при различных граничных и начальных условиях.
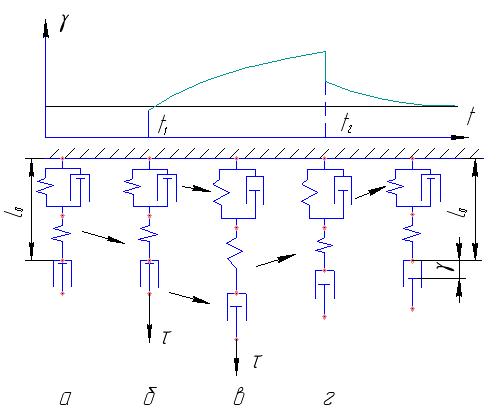
Рис.16. Кривая кинетики деформации ОТЛ (стрелки показывают места происходящих изменений)
а – нет нагрузки, б – приложено напряжение, в – ползучесть, сняли напряжение.
Итак, кривая кинетики деформации ОЛТ (см. рис. 16).
Ввиду наличия упругого элемента (который соединен последовательно с элементом Кельвина) при приложении нагрузки мгновенно возникает деформация, обозначенная на рис. 16 через γ1. Вязкий элемент тела Кельвина не дает ему (телу Кельвина) мгновенно деформироваться. Но время идет от t1 до t2, напряжение приложено и происходит постепенное нарастание деформации, которая на рис. 16 обозначена через γ1-2. Если снять напряжение, то мгновенно уменьшится деформация на величину γ1 за счет мгновенного возвращения упругого элемента к первоначальным размерам. Дальше с течением времени после разгрузки будет «работать» упругая составляющая элемента Кельвина. И, в конце концов, деформации полностью устранятся, деформированное при нагружении тело вернется к тем размерам, которые оно имело до деформации.
Мы с вами увидели пользу механической модели уже в двух планах — во-первых, она позволяет просто получить математическую модель, а, во-вторых, позволяет провести анализ поведения тела, моделью которого она является, при различных условиях его нагружения.
Казалось бы все правильно, но мы забываем при этом о том, как получается механическая модель.
Прежде мы наблюдаем, реальные материалы и их особенности при деформировании, а потом уже моделируем их механическими моделями. Так что отнесение к заслугам механической модели того, что было под рубрикой «во-вторых» — иллюзорно.
Напротив, зная особенности поведения реальных материалов, мы подправляем модель. Приведем этому пример.
Только прежде еще несколько слов о модели ОЛТ. Пуанкаре принадлежит высказывание, утверждающее, что если какое-либо физическое явление может быть представлено одной механической моделью, то оно же может быть представлено бесконечным числом других моделей. Обобщенное линейное тело нами было представлено как последовательно соединенные тела Гука и Кельвина. Те же самые свойства могут быть описаны другим способом — путем параллельного соединения тел Гука и Максвелла (рис. 17).
В порядке упражнения получите математическую модель ОЛТ в этом варианте, для чего воспользуйтесь предложенным символическим методом. Мы же приведем выкладки без всяких комментарий.
![]() (119)
(119)
![]() (120)
(120)
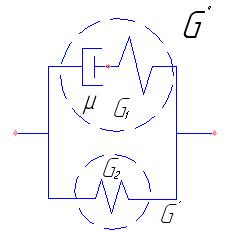
Рис. 17. Вариант модели ОТЛ
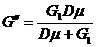 (121)
(121)

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 |




