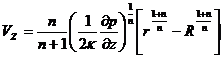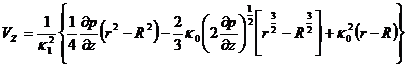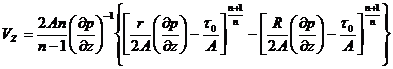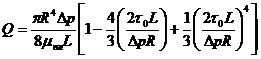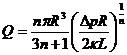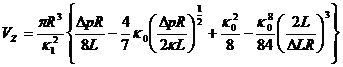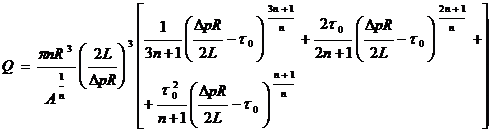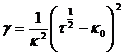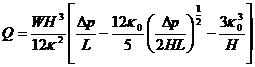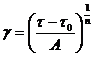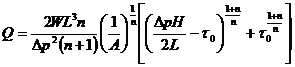Свойства макаронного теста при его обработке, например, при прохождении шнековой камеры, непрерывно изменяются. На Московской макаронной фабрике № 1 были проведены эксперименты капиллярной вискозиметрии макаронного теста для выяснения изменения свойств теста при его движении в шнековой камере прессов. Исследовали тесто, перерабатываемое на прессах ЛМБ и «Мабра». Опыты вели на капиллярном вискозиметре АКВ-5.
Математическая обработка экспериментальных данных позволила получить реологические константы, которые сведены в таблицу 9.
Таблица 9
Значения реологических констант уравнения ![]()
для теста, обрабатываемого на производственных прессах
1-й Московской макаронной фабрики
Тип пресса | Место отбора пробы | п | k |
«Мабра» | Перед шнеком | 0,49094 | 29510 ' |
После матрицы | 0,50849 | 31009 | |
ЛМБ | Перед шнеком | 0,51655 | 34698 |
После матрицы | 0,52023 | 40315 |
Из анализа результатов следует, что при движении теста в шнековом канале существенно меняются его реологические характеристики. Например, эффективная вязкость теста, прошедшего шнековую камеру пресса «Мабра», изменяется на 6—7% (при скоростях сдвига в несколько единиц сек-1), а прошедшего шнековую камеру пресса ЛМБ — на 16—17%. Анализ данных говорит также о существенном влиянии на свойства теста конструктивных параметров тестомесителей и режимов их работы. Особенно заметно сказывается влияние вида тестосмесителя на величинах показателя степени, который для теста лабораторного приготовления меняется в существенно других пределах, чем для случая теста производственного приготовления.
Изменение структурно-механических характеристик в результате взаимодействия с рабочими органами машины наблюдали также на примере массы пралине, перерабатываемой па прессе с шестеренным нагнетателем. Для выяснений реологических характеристик в процессе прохождения шестеренного пресса были проведены эксперименты по вискозиметрии массы, взятой из нижней части бункера, т. е. непосредственно перед входом в шестеренный нагнетатель пресса, и массы, прошедшей шестеренный нагнетатель (эксперименты проводились на Минской кондитерской фабрике «Коммунарка» на ротационном вискозиметре). На рис. 29 приведены кривые течения пралине «Кара-Кум». Из графиков видно, что, кроме резкого изменения коэффициентов К и n, входящих в реологическое уравнение ![]() , в результате прохождения массой шестеренного нагнетателя меняется характер кривой. Масса, не прошедшая нагнетатель, во всем исследованном диапазоне скоростей сдвига имела постоянный показатель степени п, а масса, прошедшая нагнетатель—переменный показатель степени п.
, в результате прохождения массой шестеренного нагнетателя меняется характер кривой. Масса, не прошедшая нагнетатель, во всем исследованном диапазоне скоростей сдвига имела постоянный показатель степени п, а масса, прошедшая нагнетатель—переменный показатель степени п.
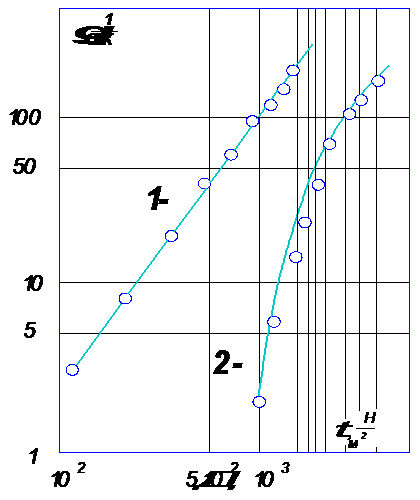
Рис. 29. Кривые течения массы пралине
«Кара-Кум», выдавливаемой шестеренным
прессом.
Полученные результаты говорят о наличии связи между способом и интенсивностью механической обработки продукта и его реологическими характеристиками. Реологические характеристики и их изменение хорошо кореллируют с качеством создаваемого продукта и возможными его вариациями. Таким образом, у специалистов появляется объективный критерий для сравнения конструктивных вариантов различных машин, перерабатывающих одни и те же продукты, .или для оценки различных режимов обработки полуфабрикатов машиной данного типа. Пробы на разных стадиях технологического процесса и экспресс-вискозиметрия дают информацию для сознательного изменения режимов обработки в целях достижения лучшего качества продукции.
§ 14. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ПРИ ТЕЧЕНИИ ПИЩЕВЫХ МАСС В ЩЕЛЕВЫХ КАНАЛАХ И ТРУБАХ
В расчетах течения пищевых масс в рабочих каналах машин во многих случаях целесообразно сложные по конфигурации каналы заменять геометрически упрощенными каналами или их совокупностью (расчетными схемами). Простейшими расчетными схемами являются щелевой канал и труба круглого сечения, течение в которых пищевых масс будут здесь рассматриваться.
Задачи определения скоростей частиц пищевых сред в различных каналах лежат в основе механических расчетов многих пищевых машин и технологических процессов. От точности решения этих задач зависит достоверность расчетных моделей транспортирующих устройств, формующего оборудования, смесителей, сепараторов, мельниц, фильтров и другого оборудования, на котором реализуются механические процессы переработки пищевых материалов. Эти же задачи встают как сопутствующие при создании расчетных моделей оборудования, предназначенных для реализации в качестве основных тепловых, химических и биологических процессов.
При решении задач определения вообще скоростей приходится сталкиваться с большим количеством разделов общей механики. Встают задачи классической кинематики и динамики материальных точек, твердых тел и механических систем, механики сыпучих тел, механики газов и их смесей с сыпучими телами, механики процессов фильтрации, механики жидкостей и жидкообразных дисперсных систем.
Если ограничиться рассмотрением скоростей движения жидкостей и жидкообразных сред, то следует перечислить тоже большое количество подходов и теории в решении этих задач. Это динамика невязкой жидкости и безвихревого течения, динамики вязкой жидкости и вихревого движения, теория подобия и анализа размерностей, теория пограничного слоя, теория крыла, волновых движений, глиссирования, кавитации, удара и т. д.
Такое громадное количество теорий связано, в частности, с тем, что, например, уравнение движения Навье-Стокса является нелинейным дифференциальным уравнением второго порядка в частных производных, решение которого в общем виде применительно к конкретным инженерным задачам приводит к большим затруднениям. Если к этому добавить еще необходимость учета уравнения состояния текущего материала и термодинамики, то решение большинства практических задач в достаточно общей постановке является почти безнадежным делом. Поэтому для каждого конкретного процесса течения стремятся составить упрощенную систему уравнений, отражающую важнейшие свойства процесса и в то же время разрешимую математически.
Здесь рассмотрим ряд задач определения скоростей частиц высоковязких несжимаемых пищевых сред в щелевых и круглых каналах при стационарном и изотермическом течении. Несмотря на такие сильные ограничения, получаемые при этом формулы дают полезную для инженерных расчетов информацию.
В щелевых каналах можно пренебречь влиянием боковых стенок и расчетную схему представить в виде течения между ДВУМЯ параллельными пластинами (рис. 30).
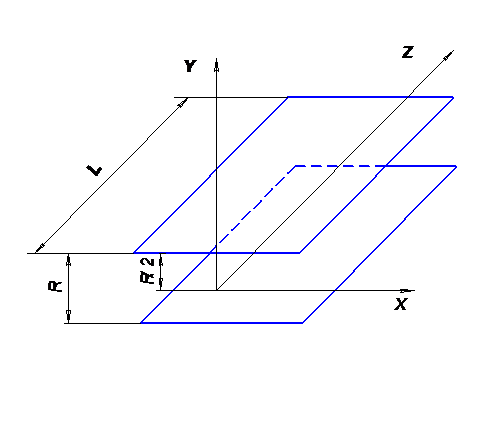
Рис. 30. Схема к расчету течения в щелевом канале.
Математически задача построена на следующих дифференциальных уравнениях, упрощающих положениях и краевых условиях:
1. Уравнение неразрывности:
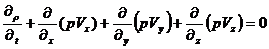 (209)
(209)
где
р — плотность,
t — время,
х, у, z — пространственные координаты на рис. 30, Vx, Vy, Vz — компоненты скорости.
Полагая Vх = Vу = 0 и p = Const, получим ![]() =0 и Vz(Z) = Const
=0 и Vz(Z) = Const
2. Уравнения движения
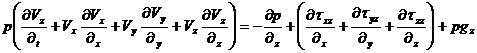 (210)
(210)
где
![]() – перепад давлений,
– перепад давлений,
![]() — компоненты касательных напряжений,
— компоненты касательных напряжений,
gz — составляющая ускорения свободного падения.
Считая gz=0 и τxz= τ =0, с учетом упрощений уравнения (209), получим
![]() (211)
(211)
3. Краевые условия (условия прилипания) имеют вид:
![]() (212)
(212)
и из условия симметрии потока запишем 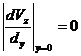
4. Задача (211), (212) решается при определенном уравнении состояния среды. Например, для ньютоновской жидкости
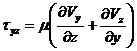 (213)
(213)
где μ — коэффициент динамической вязкости.
С учетом следствий из уравнения (209) формула (213) будет иметь вид:
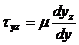 (214)
(214)
Распределение скоростей получим, решая уравнения (211), (212) и (214) совместно:
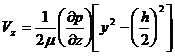 (215)
(215)
В таблице 10 даны формулы распределения скоростей между пластинами для ряда неныотоновских жидкостей. Получение этих формул является полезным упражнением при изучении данного курса.
Распределение скоростей в цилиндрическом канале круглого сечения получают, решая краевую задачу, аналогичную задаче (211), (212), (213), только в цилиндрических координатах. В таблице 11 даны формулы распределения скоростей в трубах для ряда неньютоновских жидкостей.
Распределение скоростей можно получить также, используя вариационный принцип Мосолова-Мясникова вида:
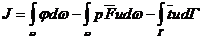 (216)
(216)
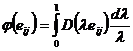 (217)
(217)
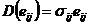 (218)
(218)
Реологические уравнения | Формула распределения скоростей |
1. Ньютона |
|
2. Вингмана-Шведова |
|
3. Оствальда-де-Вале |
|
4.
Кэссона |
|
5.
Гершеля-Балкли |
|
Таблица 10
Скорости течения в щелевом канале.
где — функционал, соответствующий принципу виртуальных работ для голономных диссипативных сплошных сред,
(ω —объем, заполненный средой,
Г — площадь (граница) объема,
F — внешние массовые силы,
t — внешние поверхностные силы,
u — скорость,
φ(еij) —диссипативный потенциал,
D(eij) — функция диссипации,
еij—тензор скоростей деформаций,
σij — тензор напряжений.
Для неныотоновских жидкостей функция диссипации здесь имеет вид:
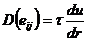 (219)
(219)
и диссипативный потенциал:
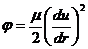 (220)
(220)
Полагая, что
 (221)
(221)
и, записав из геометрических соображений (см. рис. 31)

Рис. 31. Схема к расчету течения в трубе.
![]() (222)
(222)
можно функционал (216) представить в виде:
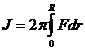 (223)
(223)
где
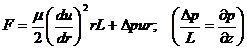 (224)
(224)
Стационарность функционала (223) обеспечивает условие Эйлера-Лагранжа:
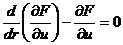 (225)
(225)
где
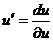
Из формул (224) и (225) получим условие стационарности вида:
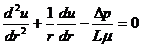 (226)
(226)
решение которого при 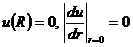 имеет уже известный по таблице 11 вид:
имеет уже известный по таблице 11 вид:
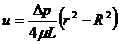 (227)
(227)
Таким путем можно получить также остальные формулы в таблице 11.
§ 15. ОПРЕДЕЛЕНИЕ РАСХОДОВ ПРИ ТЕЧЕНИИ ПИЩЕВЫХ МАСС В ЩЕЛЕВЫХ КАНАЛАХ И ТРУБАХ
Общая схема определения расходов при течении пищевых сред в рабочих каналах машин заключает в себе две задачи. Во-первых, по известным геометрическим размерам канала, перепаду давлений (или скорости движения стенок канала) и реологическому закону вязкого течения материала определяют скорости во всех точках поперечного сечения канала. Во-вторых, полученную функцию скорости интегрируют по площади поперечного сечения канала.
Большое количество моделей сдвигового течения неньютоновских пищевых масс иногда приводит к определенным математическим затруднениям при решении указанных выше задач и часто к громоздким неудобным в инженерных расчетах формулам. Например, задача определения скоростей течения среды Кэссона в зазоре между коаксиальными цилиндрами приводит к интегралу, который нельзя выразить в элементарных функциях.
Эти обстоятельства, в частности привели к выводу общих формул расхода при произвольном законе течения, y = f(τ) без
Реологические уравнения | Формула распределения скоростей |
1. Ньютона |
|
2. Вингмана-Шведова |
|
3. Оствальда-де-Вале |
|
4.
Кэссона |
|
5.
Гершеля-Балкли |
|
Таблица 11
Скорости течения в трубе.
промежуточного определения распределения скоростей. Для трубы такая формула была получена в теории капиллярных вискозиметров и имеет вид:
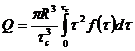 (228)
(228)
где Q — объемный расход,
R — радиус трубы,
τс — напряжение сдвига на стенке трубы,
τ —текущее значение касательных напряжений.
Величина τс определяется формулой вида:
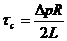 (229)
(229)
где Δр перепад давлений на длине L трубы.
Аналогичные формулы можно вывести для щелевого канала:
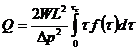 (230)
(230)
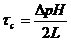 (231)
(231)
где W— ширина канала (W>>Н), Н — высота канала.
В таблицах 12 и 13 приведены некоторые формулы расхода, которые легко получить при использовании выражений (228) — (231). Отметим, что при расчетах течения сред, обладающих предельным напряжением сдвига, в нижние пределы интегралов (228) и (230) подставляется величина предельного напряжения сдвига.
Некоторые из формул в таблицах достаточно сложны и неудобны в инженерных расчетах. Если учесть, что реологические уравнения пищевых сред получают экспериментально вискозиметрированием и константы в этих уравнениях подвержены большим флуктуациям из-за различных, иногда трудно уловимых факторов, то вряд ли можно считать целесообразным всегда пытаться проводить точное интегрирование но формулам (228) и (230). При первых же признаках появления громоздкой формулы следует для расчета расхода использовать следующий простой графо-аналитический метод. Располагая реологической кривой, течения у = /(т)> необходимо для трубы построить функцию вида:
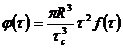 (232)
(232)
Реологические уравнения | Формула распределения скоростей |
1. Ньютона |
|
2. Вингмана-Шведова |
(Букингем-Рейнер) |
3. Оствальда-де-Вале |
|
4.
Кэссона |
|
5.
Гершеля-Балкли |
|
Таблица 12
Формулы расхода при течении в трубе
Реологические уравнения | Формула распределения скоростей |
1. Ньютона |
|
2. Бингмана-Шведова |
(по ) |
3.
Оствальда-де-Вале |
(по ) |
4.
Кэссона |
|
5.
Гершеля-Балкли |
|
Таблица 13
Формулы расхода при течении в щелевом канале.
а для щели.
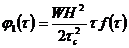 (233)
(233)
Затем, любым способом (графическое интегрирование, использование механического планиметра, просто по клеткам на миллиметровой бумаге) приближенно определить площадь под кривыми ![]() или
или ![]() , которая по величине и будет равняться расходу. Это очевидно из формул (228), (230) и геометрической интерпретации понятия определенного интеграла. Важно заметить, что данный графоаналитический способ вообще не требует аналитического описания связи
, которая по величине и будет равняться расходу. Это очевидно из формул (228), (230) и геометрической интерпретации понятия определенного интеграла. Важно заметить, что данный графоаналитический способ вообще не требует аналитического описания связи 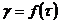 , а задача подбора вида эмпирической формулы
, а задача подбора вида эмпирической формулы ![]() не всегда простая и однозначная задача. Достаточно попытаться это сделать для, так называемых, S — образных кривых течения.
не всегда простая и однозначная задача. Достаточно попытаться это сделать для, так называемых, S — образных кривых течения.
§ 16. ОПРЕДЕЛЕНИЕ ЛИНЕЙНЫХ ПОТЕРЬ ДАВЛЕНИЯ В ТРУБАХ
По формуле Пуазейля видно, что для ньютоновских жидкостей задача определения линейных потерь давления является элементарной алгебраической задачей, однако не всегда уравнения расхода легко решаются относительно перепада давлений. Примером может являться соответствующая среде Бингама-Шведова формула Букингама-Рейнера.
Эквивалентной формуле Пуазейля является Дарси-Вейс-баха вида:
![]()
 (234)
(234)
где Δр — перепад давлений,
λ — коэффициент сопротивления,
L, D —длина и диаметр трубы,
Vср — средняя скорость течения жидкости;
Q — плотность жидкости.
Среднюю скорость определяет формула вида:
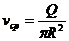 (235)
(235)
а коэффициент λ:
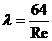 (236)
(236)
и
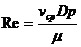 (237)
(237)
где Re — критерий Рейнольдса.
Формула (236) на логарифмической координатной сетке представляет прямую с отрицательным тангенсом наклона до наступления турбулентного режима течения. Но формулу (236) и названную выше прямую для среды Бингама-Шведова использовать нельзя. Для этой среды Б. Хэдстрем дополнил прямую ![]() на логарифмической сетке семейством
на логарифмической сетке семейством
кривых, образующих диаграмму Хэдстрема. Аналитически кривые диаграммы Хэдстрема описываются формулами вида:
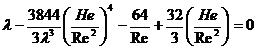 (238)
(238)
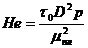 (239)
(239)
где Не — критерий Хэдстрема,
τ0 — предельное напряжение сдвига, μпл — пластическая вязкость.
Очевидно в предельном случае, когда τ0 = О формула (238) переходит в формулу (236). Поскольку величину X (в оригинале диаграммы Хэдстрема), рис. 32, используется коэффициент ![]() , но это не принципиальное отличие находят графически, то громоздкость формулы (238) не имеет практически значения.
, но это не принципиальное отличие находят графически, то громоздкость формулы (238) не имеет практически значения.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 |





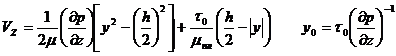 – граница жесткого слоя
– граница жесткого слоя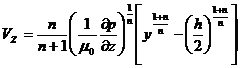
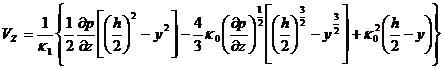
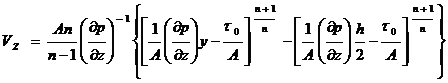
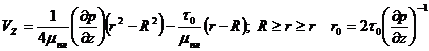 – граница жесткого ядра
– граница жесткого ядра