§ 11. ОБРАБОТКА ПО МЕТОДУ СРЕДНИХ ДАННЫХ ВИСКОЗИМЕТРИИ ПИЩЕВЫХ МАСС
В результате вискозиметрирования определенной пищевой массы на капиллярном или ротационном вискозиметрах получают таблицу пар чисел. Это, либо расходы Qi и перепады давлений ΔPi либо крутящие моменты Mi и угловые скорости ωi либо скорости сдвига ![]() и напряжения сдвига
и напряжения сдвига![]() .
.
Аналитически экспериментальные данные можно описать, применяя интерполяционные формулы Лагранжа, Ньютона, Стирлинга и Бесселя [1] при параболической интерполяции данных многочленами вида:
![]() (182)
(182)
или методами гармонического анализа при тригонометрической интерполяции, когда правая часть уравнения (182) представляется в виде тригонометрических полиномов Фурье [2]. Последние являются частным случаем ортогональной системы функций, которые можно использовать вместо многочлена (182), если степень полинома оказывается слишком большой. Кроме рядов Фурье, ортогональные системы функций представляют полиномы Лежандра, Чебышева и любые системы функций fo(xfn(x) удовлетворяющих условию:
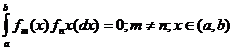 (183)
(183)
где fo(xfn(x) – система ортогональных функций,
a, b – границы отрезка определения x.
Условие (183) позволяет сравнительно просто находить коэффициенты Сп полиномов вида:
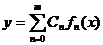 (184)
(184)
О существовании отмеченных выше способов описания экспериментальных данных полезно знать, однако в большинстве случаев практически при вискозиметрировании пищевых масс стремятся использовать 5 следующих эмпирических формул, описывающих определенные модельные среды:
![]() (Среда Ньютона) (185)
(Среда Ньютона) (185)
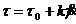 (Среда Шведова-Бингама) (186)
(Среда Шведова-Бингама) (186)
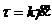 (Среда Оствальда-де-Вале или степенная жидкость) (187)
(Среда Оствальда-де-Вале или степенная жидкость) (187)
![]() (среда Гершеля-Балкли) (188)
(среда Гершеля-Балкли) (188)
![]() (среда Кэссона) (189)
(среда Кэссона) (189)
где: k1τ0, k0, k1, n – эмпирические коэффициенты.
Коэффициенты в формулах (185) — (189) можно определить методом наименьших квадратов [1, 2], однако, учитывая большие флуктуации вязкостных свойств пищевых масс под влиянием многочисленных факторов (дисперсионный и химический состав, температура, давление, микробиологические процессы и т. д.), можно использовать более простой метод средних. Возникающие при этом погрешности относительно метода наименьших квадратов малы и не имеют обычно принципиального значения. Особенно выгоден метод средних при ручном счете на клавишных ЭЦВМ, значительно сокращая время счета (по сравнению с методом наименьших квадратов).
Аналитически метод средних сводится к линеаризации (если это необходимо) формул (185—189), составлению избыточной системы некорректных уравнений вида (185—186) при подстановке экспериментальных величин ![]() , и последующему решению этой системы относительно эмпирических коэффициентов. Легко дать этим операциям также наглядную геометрическую трактовку.
, и последующему решению этой системы относительно эмпирических коэффициентов. Легко дать этим операциям также наглядную геометрическую трактовку.
Рассмотрим два примера. Для ньютоновской жидкости система уравнений будет иметь вид:
![]() , i = 1, 2, …, n (190)
, i = 1, 2, …, n (190)
где n - число экспериментальных точек
Очевидно коэффициент K, как средний, определяется формулой вида
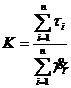 (191)
(191)
В случае среды Гершеля-Балкли начинают с определения величины τо[2]. Для этого располагают пары чисел ![]() порядке возрастания
порядке возрастания ![]() . Затем вычисляют геометрическое среднее значение
. Затем вычисляют геометрическое среднее значение ![]() по формуле:
по формуле:
![]() , (192)
, (192)
где ![]() и
и ![]() - соответственно минимальное и максимальное значения скоростей сдвига
- соответственно минимальное и максимальное значения скоростей сдвига ![]() ,
,
p – число экспериментальных точек
Линейной интерполяцией между ближайшими ![]() значениями
значениями![]() и
и ![]() соответственно значениями
соответственно значениями ![]() и
и ![]() , определяют геометрическое среднее касательное напряжение
, определяют геометрическое среднее касательное напряжение ![]() по формуле:
по формуле:
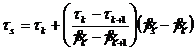 (193)
(193)
Процесс нахождения ![]() и
и ![]() можно формализовать при последовательном вычислении пар разностей
можно формализовать при последовательном вычислении пар разностей ![]() и начиная от
и начиная от ![]() до нарушения условия
до нарушения условия
![]() (194)
(194)
Формула (194) важна при программировании описываемых вычислений для расчетов на ЭЦВМ. Величина предельного напряжения сдвига может быть тогда определена по формуле вида:
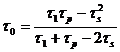 (195)
(195)
остальные коэффициенты по формулам вида:
![]()
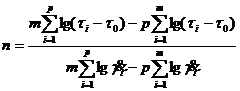 (196)
(196)
![]() (197)
(197)
где ![]() - целочисленные значения отношения
- целочисленные значения отношения ![]() .
.
Приведем здесь конечные формулы для остальных случаев, предлагая их вывод проверить в качестве упражнения читателю.
Среда Бингама-Шведова, формула (186):
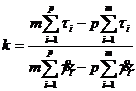 (198)
(198)
![]() (199)
(199)
Среда Оствальда-де-Вале, формула (187):
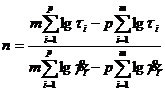 (200)
(200)
![]() (201)
(201)
Среда Кэссона, формула (189):
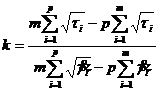 (202)
(202)
![]() (203)
(203)
Естественно, формулы (можно использовать для обработки по методу средних любых экспериментальных данных, если не придавать вычисляемым коэффициентам узкий физический смысл реологических констант в формулах (
§ 12. КОНИЧЕСКИЕ ПЛАСТОМЕРЫ
И ОЦЕНКА ПРИБОРНОЙ ИНВАРИАНТНОСТИ
ИЗМЕРЯЕМЫХ ИМИ ВЕЛИЧИН
Наряду с капиллярными и ротационными вискозиметрами в реометрии пищевых масс широко используются конические пластометры (например, КП-3), теорию которых разработали , , Широков М. Ф. и [1, 2, 3].
Определяемые на конических пластометрах предельное напряжение сдвига и пластическая прочность имеют большое значение в исследованиях пищевых масс. Эти величины прямо связаны с условиями формосохраняющей способности изделий, что необходимо учитывать при подборе режимов формования, определении предельно допустимых размеров изделий и условий хранения. Например, по , критическую высоту hкр формосохранения изделий определяет формула вида:
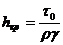 ,
,
где ![]() - предельное напряжение сдвига,
- предельное напряжение сдвига,
![]() - плотность материала,
- плотность материала,
![]() - удельный вес материала.
- удельный вес материала.
Идея конических пластомеров заключается в утверждении, что по величине глубины погружения конуса в материал под воздействием вертикальной силы можно определить предельное напряжение сдвига материала. Основная формула обработки экспериментальных данных, полученных на коническом пластометре, имеет вид:
![]() (204)
(204)
где ![]() – геометрическая константа конуса, зависящая от угла при его вершине
– геометрическая константа конуса, зависящая от угла при его вершине
![]() – величина вертикальной внедряющей силы,
– величина вертикальной внедряющей силы,
![]() - глубина погружения конуса
- глубина погружения конуса
Поскольку функция (205) линейна по отношению к аргументу ![]() то в практических опытах обычно нагрузку Р ступенчато увеличивают и измеряют при этом прирост h, что позволяет более точно рассчитывать величину то последняя величина предполагается независимой от величины угла конуса, силы Р и глубины hив этом смысле инвариантна по отношению к параметрам прибора. Здесь ситуация такая же, как при испытаниях материалов нa растяжение, где, например, предел прочности материала не должен зависеть от диаметра и длины растягиваемого образца.
то в практических опытах обычно нагрузку Р ступенчато увеличивают и измеряют при этом прирост h, что позволяет более точно рассчитывать величину то последняя величина предполагается независимой от величины угла конуса, силы Р и глубины hив этом смысле инвариантна по отношению к параметрам прибора. Здесь ситуация такая же, как при испытаниях материалов нa растяжение, где, например, предел прочности материала не должен зависеть от диаметра и длины растягиваемого образца.
Повышение физической достоверности результатов измерений и исключение влияния различных масштабных и других факторов являются иногда очень сложной задачей и требует глубокого теоретического обоснования методов измерения. Например, удовлетворительная основная теория капиллярных вискозиметров была разработана лишь в 1929 году (формула Рабиновича-Муни), а ротационных — в 1953 году (формула Павловского). Поучительной в этом отношении является также история конических пластометров.
В работе [3] для расчета геометрического коэффициента К была дана формула вида:
![]() , (206)
, (206)
где ![]() - угол при вершине конуса.
- угол при вершине конуса.
Через 9 лет в работе [2] была предложена формула вида:
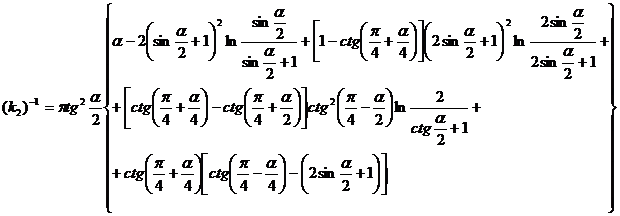
(207)
Появление новой формулы было связано с тем, что величины предельного напряжения сдвига, вычисляемые по формуле (205) с использованием коэффициента К1, были в 2 раза больше, чем получаемые на пластометрах принципиально других конструкций (пластометры с коаксиальными цилиндрами, приборы типа Толстого, Вейлера-Ребиндера). Формула (205) при угле ![]() = 60° действительно обеспечивает требуемую корректировку
= 60° действительно обеспечивает требуемую корректировку ![]() . Однако при уменьшении угла а уже при
. Однако при уменьшении угла а уже при ![]() = 20° обнаруживается, что
= 20° обнаруживается, что ![]() (см. табл. 2).
(см. табл. 2).
Таблица 2
Геометричиские коэффициенты конического пластометра
| К1 | К2 | К3 | |
1. | 20 | 1,75 | 1,83 | 0,61 |
2. | 30 | 1,11 | 0,959 | 0,456 |
3. | 45 | 0,658 | 0,416 | 0,268 |
4. | 60 | 0,416 | 0,214 | 0,164 |
5. | 90 | 0,159 | 0,073 | 0,0657 |
Однако, этим не ограничиваются возникшие трудности, которые можно было бы обойти, указав предел допустимых изменений у прибора угла ![]() от 90° до 30°, и подобные рекомендации действительно можно встретить в литературе.
от 90° до 30°, и подобные рекомендации действительно можно встретить в литературе.
Новые возможности анализа сложившейся ситуации дает использование элементов кибернетической теории распознавания образов, на связь которой с реометрией указал X. с сотрудниками [4]. В частности, среди различных методов распознавания образов в реометрии используется параметрический метод распознавания, при котором совокупность измеренных реологических параметров (матрица параметров) ставится в соответствие с признаками (параметрами) реологических моделей сред, в результате чего распознается образ материала и материал относится к той или иной категории или группе. По матрице параметров могут также сравниваться различные материалы, распознаваться их различие, если оно завуалировано разбросом данных измерений.
В данной задаче с коническим пластометром можно поставить в некотором смысле обратную задачу задаче распознавания образа материала. Производя по рандомизированному плану измерения на одном и том же материале, мы физически сохраняем образ материала неизменным. Если при этом варьировать угол конуса, то параметрическим методом мы можем распознать влияние (если оно существует) угла а на величину то, чего не должно быть, поскольку изменение угла конуса не должно изменять реологическое свойство материала— предельное напряжение сдвига. Соответствующие опыты показывают, что при использовании коэффициента Ki такое влияние существует в интервале ![]() =30°—90°.
=30°—90°.
Возникшая задача усовершенствования формулы (207) окончательно не решена до сих пор; можно лишь предложить поправку вида:
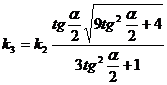 (208)
(208)
и заметить, что
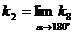
Проверка формулы (208), которая получена при достаточно грубых допущениях, была проведена экспериментально с использованием параметрического метода теории распознавания образов и показала, что формула (208) обеспечивает получение независимых от а величин предельного напряжение сдвига и в этом смысле предпочтительнее формулы (207).
Очевидно, метод вариации параметров прибора с последующим использованием аппарата распознавания образов, может быть использован в любых реометрических исследованиях при оценке приборной инвариантности измеряемых величин.
§ 13. РЕОЛОГИЧЕСКИЕ (СТРУКТУРНО-МЕХАНИЧЕСКИЕ) СВОЙСТВА НЕКОТОРЫХ ИЗДЕЛИЙ И ПОЛУФАБРИКАТОВ ПИЩЕВОЙ ПРОМЫШЛЕННОСТИ
Здесь приведены обобщения исследований, объектом которых являлись макаронное, хлебопекарное и кондитерское тесто, конфетные массы и некоторые виды сырья кондитерской и хлебопекарной промышленности. Все исследованные материалы представляют собой структурированные дисперсные системы, обладающие сложным комплексом вязкоупругопластических свойств, проявляемых в том или ином сочетании, в зависимости от условий, в которых находится исследуемый материал.
Обобщение сделано на основании исследований, проведенных в основном на стандартных приборах, видоизменных с учетом специфических особенностей пищевых масс. Общее количество проанализированных реологических измерений равнялосьПроведена математическая обработка и анализ 819 полученных в экспериментах кривых течения. (Макаронное тесто — 3033 измерения, 227 кривых течения; хлебопекарное тесто—1861 и 95; кондитерское тесто — 2869 и 151; пралине— 8383 и 254; восточные сладости — 864 и 54; помадные и другие массы— 1279 и 38).
Исследования полуфабрикатов и изделий пищевой промышленности, проведенные при температурных режимах, характерных для производственных условий переработки каждого из материалов, показали весьма существенные расхождения в свойствах исследованных продуктов. Так, вязкостные характеристики различных материалов отличались на 5—6 десятичных порядков. На рис. 27 приведены типичные кривые течения для исследованных материалов, а в таблице 3 соответствующие реологические константы.
Примечание. Данные, полученные при исследовании на ротационном вискозиметре, обозначены значком РВ, на капиллярном— KB, на автоматическом капиллярном — АКВ.
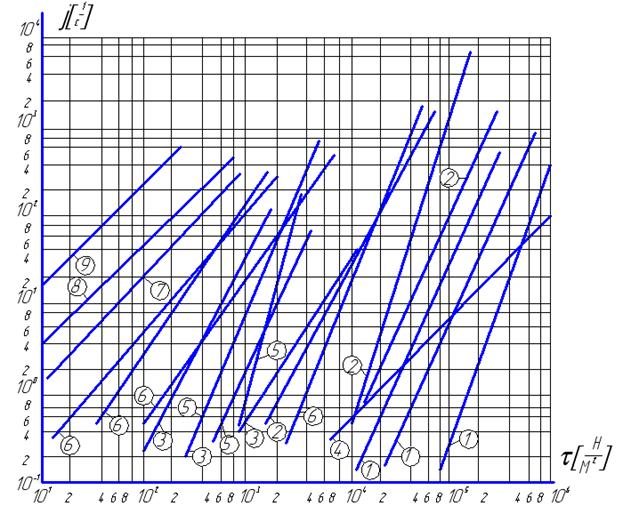 Рис. 27. Кривые течения различных пищевых материалов
Рис. 27. Кривые течения различных пищевых материалов
1.Макаронное тесто 3. Хлебопекарное тесто 5.Помадная паста 7. Мед
Кондитерское тесто 4. Нуга 6. Пралине 8. Сгущенное молоко 9. Сливочное масло
Таблица 3
Реологические константы К и n (уравнения ![]() )
)
исследованных пищевых полуфабрикатов и изделий
Название | Тип прибора | К | n |
Сливочное масло | РВ | 0,9 | 0,87 |
Мед пчелиный | РВ | 3,5 | 0,95 |
“Космос” | РВ | 7 | 0,88 |
“Чиполлино” | РВ | 27 | 0,77 |
Гидрожир | РВ | 40 | 0,46 |
“Кара-Кум” | РВ | 50 | 0,63 |
“Белочка” | РВ | 77 | 0,87 |
“Чародейка” | РВ | 97 | 0,58 |
“Таганай” | РВ | 149 | 0,60 |
Тесто для розанчиков W=36,7% | КВ | 172 | 0,51 |
“Ромашка” | РВ | 484 | 0,37 |
Тесто для розанчиков W=35,1% | КВ | 770 | 0,42 |
“Виктория” | РВ | 930 | 0,26 |
Тесто для розанчиков W=33,9% | КВ | 1420 | 0,57 |
“Метелица” | КВ | 1900 | 0,47 |
Тесто, спортивные галеты | АКВ | 2250 | 0,47 |
“Чародейка” | КВ | 3145 | 0,38 |
Тесто сахарное | АКВ | 11400 | 0,28 |
Тесто затяжное | АКВ | 13300 | 0,40 |
Нуга кунжутная | КВ | 18100 | 0,88 |
Макаронное тесто (лабораторное)W=32%, T=3270 | КВ | 20600 | 0,42 |
Тесто сахарное | АКВ | 31400 | 0,34 |
Макаронное тесто (производственное) | АКВ | 34300 | 0,506 |
Нуга шоколадная | КВ | 43600 | 0,53 |
Макаронное тесто (лабораторное)W=30%, T=3210 | КВ | 45600 | 0,41 |
Макаронное тесто (производственное) | АКВ | 61400 | 0,494 |
Макаронное тесто (лабораторное)W=28%, T=3160 | КВ | 123000 | 0,31 |
Свойства макаронного теста.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 |




