Исследование операций в экономике (стр. 1 )

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

Государственное образовательное учреждение высшего профессионального образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

___________________________________________________________________________________________

ИССЛЕДОВАНИЕ ОПЕРАЦИЙ

В ЭКОНОМИКЕ

Учебное пособие

Издательство
Томского политехнического университета

2011

ББК Ув611я73

УДК 330.43(075.8)

К17

К17 Исследование операций в экономике: учебное пособие / . – Томск: Изд-во Томского политехнического университета, 2007. – 92 с.

В учебном пособии излагаются основы применения математических моделей к решению экономических задач. Большое внимание уделяется линейному программированию, транспортным и двойственным задачам, элементам теории игр и массового обслуживания, сетевому планированию и управлению. Учебный материал сопровождается достаточным числом решенных задач. Пособие содержит задания для самостоятельной работы студентов.

ББК Ув611я73

УДК 330.43(075.8)

Рекомендовано к печати Редакционно-издательским советом

Томского политехнического университета

Рецензенты

Доктор техн. наук, профессор ТПУ

Канд. физ.-мат. наук, доцент ТГУ

Канд. физ.-мат. наук, доцент ТГУ

© Томский политехнический университет, 2011

© Оформление. Издательство Томского политехнического университета, 2011

© , 2011

ОГЛАВЛЕНИЕ

Введение.......................................................................................... 4

1. Линейное программирование.............................................. 6

1.1. Формулировка задачи и ее геометрическое истолкование........ 7

1.2. Экономическая интерпретация задач линейного

программирования........................................................................... 10

1.3. Решение задачи линейного программирования методом последовательного улучшения плана (симплексным методом).................................................... 15

1.4. Метод множителей Лагранжа.................................................... 21

1.5. Двойственные задачи................................................................. 27

1.6. Транспортная задача................................................................. 33

Контрольные вопросы...................................................................... 40

2. Теория игр...................................................................................... 41

2.1. Классификация игр..................................................................... 43

2.2. Другие термины и понятия......................................................... 44

2.3. Геометрическая интерпретация игры 2x2................................. 49

2.4. Приведение матричной игры к задаче линейного

программирования................................................................................. 52

Контрольные вопросы....................................................................... 58

3. Сетевое планирование и управление............................ 58

3.1. Сетевая модель и ее основные элементы.................................... 59

3.2. Правила построения сетевых графиков..................................... 61

3.3. Временные параметры сетевых графиков................................. 62

3.4. Сетевое планирование в условиях неопределенности............... 65

3.5. Коэффициент напряженности..................................................... 67

Контрольные вопросы....................................................................... 72

4. СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ.............................. 72

4.1. Структура и классификация систем массового обслуживания. 72

4.2. Марковский процесс................................................................... 75

4.3. Системы массового обслуживания с отказами.......................... 76

4.4. Системы массового обслуживания

с неограниченным ожиданием........................................................... 79

4.5. Системы массового обслуживания с ожиданием

и ограниченной длинной очереди.......................................................... 81

4.6. Замкнутые системы массового обслуживания........................... 84

Контрольные вопросы....................................................................... 88

Список ЛИТЕРАТУРЫ................................................................. 89

Приложение Таблица значений функции Лапласса......................... 90

ВВЕДЕНИЕ

Для изучения различных экономических явлений экономисты используют их упрощенные формальные описания, называемые экономическими моделями. Строя модели, они выявляют существенные факторы, определяющие исследуемое явление, и отбрасывают детали, несущественные для решения поставленной проблемы. Формализация основных особенностей функционирования экономических объектов позволяет оценить возможные последствия воздействия на них и использовать такие оценки в управлении.

Исследование операций – научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее эффективного управления различными организационными системами.

Управление любой системой реализуется как процесс, подчи­няющийся определенным закономерностям. Их знание помогает определить условия, необходимые и достаточные для осуществления данного процесса. Для этого все параметры, характеризующие процесс и внешние условия, должны быть количественно определены, измерены. Следовательно, цель исследования операций – количественное обоснование принимаемых решений по организации управления.

При решении конкретной задачи управления применение методов исследования операций предполагает:

• построение экономических и математических моделей для задач принятия решения в сложных ситуациях или в условиях неопределенности;

• изучение взаимосвязей, определяющих впоследствии принятие решений, и установление критериев эффективности, позволяющих оценивать преимущество того или иного варианта действия.

«Исследование операций», в частности в финансово-экономической сфере и бизнесе, помогает лицу, принимающему решение, произвести критический анализ ситуации и в результате более обоснованно и последовательно проводить определенную политику или стратегию поведения при решении сложных, комплексных проблем.

Существуют различные подходы к принятию решений: психологический, на основе метода аналогий; интуитивный, на основе предшествующего опыта; на основе здравого смысла и т. п. Однако принимать управленческие и иные решения в экономике, в сфере технологии производства, в финансовой области, в бизнесе и других отраслях хозяйства с помощью только личного опыта, здравого смысла и интуиции мало эффективно, а порой и ошибочно. Сложный характер рыночной экономики предъявляет более серьезные требования к обоснованию принятия решений, хотя и перечисленные нельзя абсолютно сбрасывать со счета. Одним из способов удовлетворения этих требований является постановка проблемы принятия решений на математическую основу. В этом нет ничего необычного, поскольку современная экономическая наука существенно опирается на математическое моделирование экономических процессов и пронизана различным математическим аппаратом, а применяющийся в ней математический язык позволяет более определенно и однозначно формулировать экономические факты и законы.

В создание современного математического аппарата и развитие многих направлений исследования операций большой вклад внесли российские ученые , , и многие другие. Особо следует отметить роль академика , который в 1939 г сформулировал новый класс условно-экстремальных задач и предложил универсальный метод их решения, положив начало новому направлению прикладной математики – линейному программированию.

Значительный вклад в формирование и развитие исследования операций внесли зарубежные ученые Р. Акоф, Р. Беллман, Г. Данциг, Г. Кун, Дж. Нейман, Т. Саати, Р. Черчмен, А. Кофман и др.

Методы исследования операций, как и любые математические методы, всегда в той или иной мере упрощают, огрубляют задачу, отражая порой нелинейные процессы линейными моделями, стохастические системы – детерминированными, динамические процессы – статическими моделями и т. д. Жизнь богаче любой схемы. Поэтому не следует ни преувеличивать значение количественных методов исследования операций, ни преуменьшать его, ссылаясь на примеры неудачных решений. Уместно привести в связи с этим шутливо-парадоксальное определение исследования операций, сделанное одним из его создателей Т. Саати, как «искусства давать плохие ответы на те практические вопросы, на которые даются еще худшие ответы другими методами».

«Исследование операций», в частности в финансово-экономической сфере и бизнесе, помогает лицу, принимающему решение, произвести критический анализ ситуации и в результате более обоснованно и последовательно проводить определенную политику или стратегию поведения при решении сложных, комплексных проблем.

1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

В данном учебном пособие приводятся в очень упрощенной форме идеи нескольких методов математического программирования, наиболее часто применяемых для поиска оптимальных экономических решений. Предполагается, что постановка задачи поиска оптимального решения и решение самой задачи осуществляется совместно экономистом и математиком-исследователем. Экономист знает идеи основных математических методов и формулирует задачу в экономических категориях. Математик-исследователь осуществляет перевод экономических категорий на язык формул, выбирает математический метод решения задачи и осуществляет его программную реализацию. Довольно часто задачи поиска оптимальных экономических решений имеют несколько критериев оптимальности. Критерии оптимальности и ограничения задаются линейными или нелинейными функциями.

На практике постоянно встречаются такие ситуации, когда достичь какого-то результата можно не одним, а многими различными способами. В подобной ситуации может оказаться и одно предприятие и целая отрасль, если необходимо определить, как использовать имеющиеся в их распоряжении ресурсы, чтобы добиться максимального выхода продукции. Естественно, при большом количестве решений выбирается наилучшее. Математически это обычно сводится к нахождению наибольшего и наименьшего значения некоторой функции, то есть к задаче: найти max (min) f(x), при условии, что переменная x пробегает данное множество X.

Записывают так: f(x) max (min), xX.

Определенная таким образом задача называется задачей оптимизации. Множество Х называется допустимым множеством, а f(x) – целевой функцией.

Очень многое зависит от того, в каком виде задается множество Х.

Чаще всего это система неравенств: ,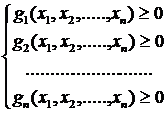

где (x1,x2,….,xn) – координаты точки х в Rn (n-мерном пространстве), а gi – некоторые функции. Таким образом, надо найти экстремум функции f(x) при заданной системе ограничений. Но понятно, что следует найти не только само значение max (min), но и точку (или точки, если их несколько), в которых это значение достигается. Такие точки называются оптимальными решениями. Задачи подобного рода называются задачами математического программирования.

В большинстве случаев в число ограничений входят условия неотрицательности переменных: x1 ≥ 0, x2 ≥ 0,…., xn ≥ 0, которые вытекают из реального экономического смысла этих чисел и называются тривиальными ограничениями.

В зависимости от характера функций f,g1, g2,….gn различают разные виды математического программирования. Наиболее простой и часто встречающийся случай, который мы и будем изучать, – когда эти функции являются линейными, то есть каждая из них имеет вид . Тогда говорят о задаче линейного программирования. Линейное программирование оформилось как отдельный раздел прикладной математики в 40–50 гг. ХХ века, когда выяснилось, что целый ряд задач из сферы планирования и управления может быть сформулирован в виде задачи линейного программирования. Подсчитано, что в настоящее время ≈ 80–85 % всех решаемых на практике задач оптимизации относится к задачам линейного программирования.

1.1.  Формулировка задачи и ее геометрическое истолкование

Чтобы показать, как решить задачу графическим способом, необходимо ввести некоторые понятия. Любое xX называется допустимым решением (планом). Допустимое решение, дающее max (min) f(x), называется оптимальным решением (планом). Неравенства называются ограничениями. Решение системы всех неравенств называется областью допустимых решений. Задачи на max и min идентичны, так как они сводятся друг к другу путем умножения целевой функции на (–1), то есть max f(x)= – min (–f(x)).

Таким образом, необходимо найти оптимальное значение функции (минимум или максимум) в области допустимых решений.

Наиболее часто встречаются две разновидности задач линейного программирования:

1. Каноническая (основная). Система ограничений, помимо тривиальных ограничений, включает в себя только уравнения.

2. Стандартная (симметричная). Система ограничений состоит только из неравенств.

В зависимости от способа решения задачи, необходимо, чтобы она была представлена в той или другой форме.

Эти две разновидности легко сводятся одна к другой.

Пример решения задачи:

1. Стандартный вид Канонический вид

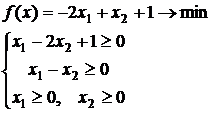
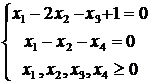
2. Канонический вид

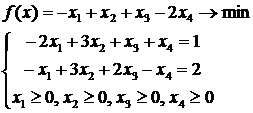
Решая систему линейных уравнений, получим: 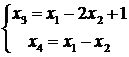. Подставляя найденные значения в целевую функцию и исключая найденные переменные из системы ограничений, получим стандартный вид задачи линейного программирования:

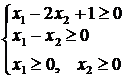
Множество решений (планов) основной задачи линейного программирования образует выпуклый многогранник. Каждая вершина этого многогранника определяет опорный план. В одной из вершин (то есть для одного из опорных планов) значение целевой функции является оптимальным, то есть max (min). Если значение max (min) функция принимает более чем в одной вершине, то это же значение она принимает в любой точке, являющейся выпуклой линейной комбинацией данных вершин. Иными словами, если оптимальное значений функции достигается в двух вершинах многоугольника, то оно будет одинаковым не только в этих вершинах, но и в любой точке отрезка, соединяющего эти вершины.

Вершину многогранника решений найти сравнительно просто, если задача, записанная в стандартной форме, содержит не более двух переменных, так как в этом случае многогранник можно изобразить на плоскости, вершина находится как точка пересечения двух прямых, которые задают ограничения в системе.

Пример решения задачи.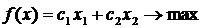

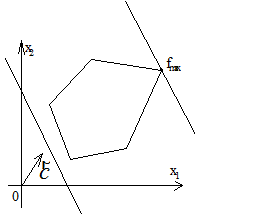
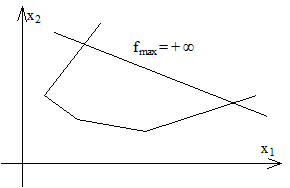
Рис. 1.1. Задача имеет Рис. 1.2. Целевая функция

единственное решение не ограничена

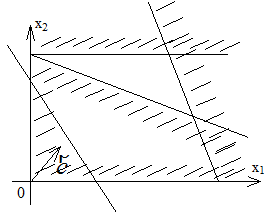
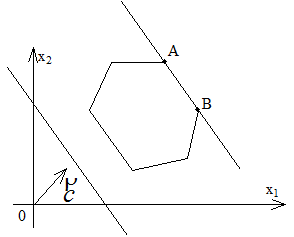
Рис. 1.3. Система ограничений Рис. 1.4. Максимальное значение

несовместна функция принимает на отрезке АВ

Пример решения задачи.

Найти max и min функции 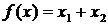при заданной системе ограничений:

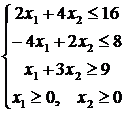
Построим многоугольник решений:

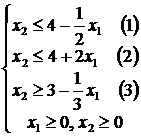
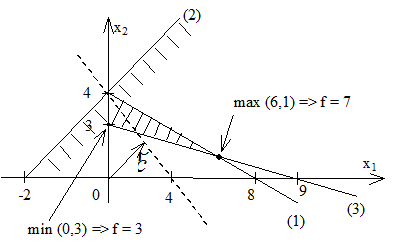
Рис. 1.5. Решение задачи графическим методом

Задание для самостоятельной работы. Решить задачу линейного программирования графическим способом.

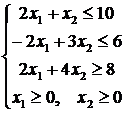
1.2. Экономическая интерпретация

задач линейного программирования

1.  Задача об использовании ресурсов (планировании производства).

Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

Введем следующие обозначения:

хj – число единиц продукции Pj, запланированной к производству,

bi – запас ресурса Si,

aij – число единиц ресурса Si, затрачиваемое на единицу продукции Pj (эти числа называют технологическими коэффициентами),

cj – прибыль от реализации продукции Pj.

Тогда модель задачи будет иметь вид:

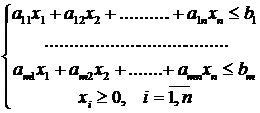
Рассмотрим задачу с конкретными данными.

Прибыль от реализации единицы продукции Р1 составляет 2 рубля, а от единицы продукции Р2 – 3 рубля. Данные о запасах ресурсов и количестве ресурсов, необходимых для изготовления единицы продукции, сведены в следующую таблицу.

Таблица 1.1

Данные задачи об использовании ресурсов

Вид ресурса	Запас ресурса	Число единиц ресурса, затрачиваемых на изготовление единицы продукции
Р1	Р2
S1	18	1	3
S2	16	2	1
S3	5	---	1
S4	21	3	---

Экономико-математическая модель данной задачи будет иметь вид:

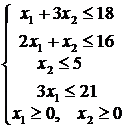
2.  Задача составления рациона (о диете, о смесях), или технологическая задача.

Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела.

Введем обозначения:

xj – число единиц корма j-го вида;

bi – необходимый минимум содержания в рационе питательного вещества Si ;

aij – число единиц питательного вещества Si в единице корма j-го вида;

cj – стоимость единицы корма j-го вида.

Тогда экономико-математическая модель задачи запишется следующим образом:

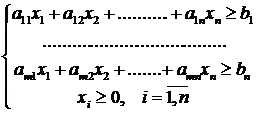
Рассмотрим задачу с конкретными данными.

Стоимость 1 кг корма вида I – 4 рубля, а вида II – 6 рублей. Используя данные таблицы, необходимо составить такой рацион питания, чтобы стоимость его была минимальной и содержание каждого вида питательных веществ было не менее установленного предела.

Таблица 1.2

Данные задачи о рационе питания

Питательное вещество	Необходимый мин. пит. веществ	Число единиц питательного вещества в 1 кг корма
I	II
S1	9	3	1
S2	8	1	2
S3	12	1	6

Модель задачи будет иметь вид:

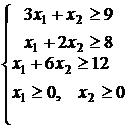
3.  Задача об использовании мощностей (задача о загрузке оборудования).

Предприятию задан план производства продукции по времени и номенклатуре: требуется за время Т выпустить n1, n2,……nk единиц продукции P1, P2,……Pк. Продукция производится на станках S1, S2, …….Sm. Для каждого станка известны производительность aij (то есть число единиц продукции Pj, которое можно произвести на станке Si в единицу времени) и затраты bij на изготовление продукции Pj на станке Si в единицу времени.

Необходимо составить такой план работы станков (то есть так распределить выпуск между станками), чтобы затраты на производство всей продукции были минимальными.

Экономико-математическая модель задачи.

Обозначим xij – время, в течение которого станок Si будет занят изготовлением продукции Pj. Так как время работы каждого станка ограничено и не превышает Т, то справедливы следующие неравенства:

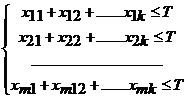
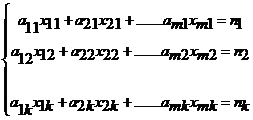
4.  Технологическая задача (о раскрое материала).

Найти план раскроя, обеспечивающий максимальное число комплектов.

Для изготовления брусьев длиной 1,2 м, 3 м и 5 м в соотношении 2:1:3 на распил поступает 195 бревен длиной 6 м. Определить план распила, обеспечивающий максимальное число комплектов.

Составим модель задачи.

Определим сначала все возможные способы распила бревен, указав соответствующее число получающихся при этом брусьев и остаток.

Таблица 1.3

Способы распила бревен

Способ распила	Число получающихся брусьев	Остаток
1,2 м	3 м	5 м
1	5	--	--	0
2	2	1	--	0,6
3	--	2	--	0
4	--	--	1	1

Через хi обозначим число бревен распиливаемых i-м способом, , а через х – число комплектов брусьев.

Тогда экономико-математическая модель задачи будет иметь вид:

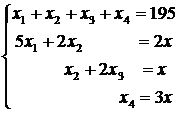
Задания для самостоятельной работы.

1. Имеем 195 бревен длиной 6 метров. Составить модель распила бревен, если необходимо получить 50 брусьев длиной 2 м, 75 брусьев длиной 3 м и 60 брусьев длиной 5 м и требуется минимизировать остатки.

2. Составить экономико-математическую модель задачи и решить ее графическим способом. Для производства двух видов изделий А и В предприятие использует два вида сырья. Данные о количестве расхода сырья и его запасы приведены в таблице. Требуется составить такой план выпуска изделий А и В, чтобы прибыль от их реализации была максимальной.

Таблица 1.4

Данные о расходе и запасах сырья

Вид сырья	Норма расхода сырья (кг) на одно изделие	Общее кол-во сырья
А	В
I	12	4	300
II	4	4	120
III	3	12	252
Прибыль от реализации одного изделия	30	40

3. По данным таблицы составить такой план загрузки станков, чтобы затраты были минимальными. Решить задачу графическим способом.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9