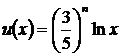Исследование операций в экономике (стр. 3 )

.

Требуется определить, как гр. Петров разместит деньги.

Решение. Первый шаг состоит в формальном представлении задачи – формализации, основные шаги которой состоят в определении переменных, ограничений, показателей эффективности и соответствующих им целевых функций.

Переменные. Альтернатива выбора гр. Петрова состоит в том, сколько денег разместить и в какой вид услуги. Пусть x1, x2 – объемы денежных средств, которые гр. Петров разместит в 1-й  и 2-й виды предлагаемых вкладов.

Ограничения. Гр. Петров собирается потратить не более 100 ден. ед., следовательно x1 + x2 £ 100. Кроме того, не имеют смысла отрицательные значения переменных, то есть x1, x2 ³ 0.

Показатели эффективности. Принимая решение о размещении денежных средств, гр. Петров стремится максимизировать полезность от получаемых денежных средств. Таким образом, определен показатель эффективности – полезность денег. Гр. Петров получит деньги трижды. Первый раз – это величина средств, оставшихся после размещения денег во вклады. Она составляет 100 – x1 – x2, а ее полезность . Далее, в конце первого года завершит свое действие 1-й вид услуги, и гр. Петров получит ден. ед., полезность которых с позиции текущего дня для него составляет 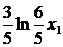. И наконец, по истечении срока действия второго договора (в конце второго года) бюджет гр. Петрова пополнит сумма в размере 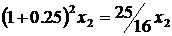, полезность которой составляет в настоящий момент величину . Таким образом, принимаемое решение приносит гр. Петрову суммарную полезность, составляющую

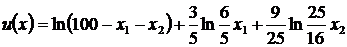. Требуется найти такие значения переменных x1, x2, чтобы величина u(x) была максимальной.

Формализованное представление задачи выглядит как

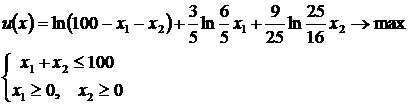
Для нахождения седловой точки составим функцию Лагранжа этой задачи:

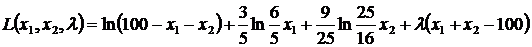
Условия дополняющей нежесткости для данной задачи представляют собой систему из трех уравнений с тремя неизвестными x1, x2, l, имеющую вид (в скобках каждого уравнения находятся частные производные функции Лагранжа по соответствующим переменным):

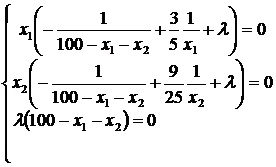
Заметим, что значения x1 = 0, x2 = 0 и 100 = x1 + x2 являются недопустимыми, так как в этих случаях не определена целевая функция. Условие 100 ¹ x1 + x2 влечет за собой  l = 0 – третье условие системы дополняющей нежесткости. Следовательно, для нахождения решения достаточно решить систему:

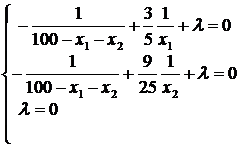
Ее решение: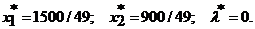

Ответ. Гр. Петров поместит 30,612 ден. ед. в первый вклад и 18,367 ден. ед. во второй вклад.

Ø  Важно помнить. Соотношения дополняющей нежесткости являются лишь необходимыми (но не достаточными) условиями седловой точки, то есть соотношения могут быть выполнены в некоторой точке, а экстремума в ней может и не быть.

Экономический смысл множителей Лагранжа

Пусть исходная задача (1.1) является формализованным представлением некоторой экономической ситуации. К задаче математического программирования приводят задачи, в которых требуется принять решение о выборе одной из допустимых альтернатив (планов), наилучшей в смысле некоторого критерия эффективности. Искомой альтернативе в задаче соответствуют переменные x. Функциональные зависимости между переменными описывают взаимодействия и взаимозависимости различных компонентов альтернативы выбора, а также представляют собой оценки затрат, необходимых для реализации той или иной альтернативы. Наличие каких-либо лимитов на ресурсы влечет за собой ограничения на выбор альтернативы. Для простоты будем считать, что все ограничения задачи (1.1) соответствуют лимитам на ресурсы, требующиеся для реализации выбираемой альтернативы.

Условия дополняющей нежесткости представляют собой систему уравнений, каждое из которых является произведением двух сомножителей. Рассмотрим одно уравнение второй группы, например 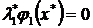. Понятно, что его решение можно представить как решение системы:

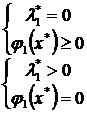
Множитель Лагранжа 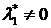соответствует границе допустимого множества, определяемой функцией j1(x*) = 0. Иными словами, если не равен нулю, то решение принадлежит границе, определяемой уравнением j1(x*) = 0. Это, в свою очередь, означает, что для оптимальной альтернативы x* первый ресурс (его затраты описывает функция j1(x)) является "узким местом" – будет израсходован полностью. Изменение имеющегося лимита для этого ресурса повлечет за собой достижение более высокого значения показателя эффективности. Если множитель Лагранжа, соответствующий первому ограничению, равен нулю, то в соответствии с (1.2) j1(x*) ³ 0. Это означает, что x* не находится на границе, задаваемой функцией j1(x*) = 0, и первоначальные лимиты на первый ресурс завышены (занижены). В частности, в решенном примере l = 0 соответствует ограничению на расход денег гр. Петровым и означает, что в оптимальном для себя случае этот гражданин не истратит всех своих средств, приобретая банковские услуги. Остаток средств составит 100 – (30,612+18,367) = 51,02, и именно такое распределение денег принесет Петрову максимальную полезность. Если ограничению соответствует ненулевой множитель Лагранжа l = 1, что означает, что в оптимальном плане данный ресурс будет израсходован полностью.

Пусть li > 0. Экономический смысл абсолютной величины множителя Лагранжа не очень прост и привязан к контексту задачи. Наиболее наглядно можно продемонстрировать его на примере задач об оптимизации производства. Пусть целевая функция F(x) некоторой задачи описывает выпуск x = (x1,..., xn)т n видов готовой продукции, а ограничения соответствуют затратам производственных факторов, используемых в некоторой производственной системе. Лимиты для m невоспроизводимых производственных ресурсов заданы как b = (b1,..., bm).  Модель такой задачи имеет вид:

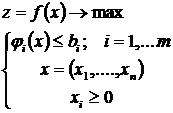
Каждому лимитированному производственному фактору соответствует множитель Лагранжа li ³ 0. Кроме того, ненулевые множители Лагранжа показывают, какие из производственных факторов в оптимальном плане будут израсходованы целиком, что в некотором роде ограничивает возможность дальнейшего увеличения выпуска. Посмотрим, как изменяется оптимальное решение (план) при малых изменениях лимитирующих величин bi. Иными словами, мы предположили, что оптимальный выпуск есть функция от запаса ресурса: x(b) = (x1(b),..., xn(b)). Показатель эффективности F(b) = F(x(b)) при этом является сложной функцией лимитов ресурсов. Все ограничения представляют собой функциональные соотношения компонентов выпуска x и, следовательно, также являются сложными функциями ji(x(b)) лимитов b.

Множитель Лагранжа li определяет прирост оптимальной величины выпускаемой продукции при изменении запаса i-го ресурса на "малую величину": 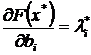. Одновременно li представляет собой верхний предел цены ресурса, которую предприятие согласно заплатить, если оно имеет в виду безубыточное его использование. Действительно, пусть прирост выпуска обеспечивается за счет прироста запаса i-го ресурса на dbi (запасы остальных ресурсов неизменны). Соответствующий прирост выпуска составит 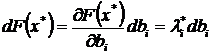. Если цена единицы данного ресурса qi, то прирост затрат составит qi dbi. Отсюда видно, что при li > qi прирост выпуска превышает прирост затрат и li = qi означает, что прирост выпуска совпадает с приростом затрат, что и объясняет смысл верхнего предела цены единицы ресурса.

Задания для самостоятельной работы.

1. Гражданин Иванов собирается разместить 200 ед. денежных средств в различные инвестиционные проекты. Известно, что абсолютная величина дохода от размера х вложенных средств по рассматриваемым трем проектам описывается зависимостями:

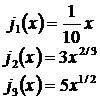
Определите, как гр. Иванову следует разместить средства, чтобы получить максимальный абсолютный доход.

2. Покупатель Петров на приобретение товаров выделил средства в размере 12 ден. ед. Ассортимент товаров насчитывает два вида, а их цены составляют 1 и 2 ден. ед. Предпочтения гр. Петрова описываются функцией полезности , где и означают количества первого и второго товаров, соответственно. Гр. Петров, предъявляя спрос на товары, стремится максимизировать получаемую при этом полезность. Определите величину спроса на товары, который будет предъявлен гр. Петровым.

3. Гражданин Иванов инвестирует средства в три проекта. Известно, что если доли вложенных в каждый из проектов средств составляют и , то средняя доходность инвестиций составит величину

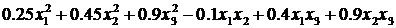
Определите, в каких долях гр. Иванов разместит средства в проекты, если известно, что он руководствуется соображениями получения средней доходности на уровне 0,08 с минимальным риском.

4. Некоторое производство выпускает три вида готовой продукции, расходуя при этом два вида ресурсов. Цены на готовую продукцию составляют 3, 4 и 1 ден. ед., нормы затрат ресурсов заданы матрицей

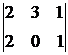
Ресурсы приобретены по ценам 0,2 и 0,1, и их первоначальный запас составил 20 и 30 ед. Определите план выпуска готовой продукции, максимизирующий коэффициент рентабельности.

1.5. Двойственные задачи

Оптимальное решение задачи линейного программирования определяется теми значениями параметров модели, которые они имели в момент ее формирования и построения. В реальной экономике значения параметров, формирующих модель, с течением времени или под воздействием каких-либо обстоятельств могут меняться. В связи с этим особый интерес представляют методы, позволяющие определить изменения в оптимальном решении, обусловленные изменениями значений параметров модели. Одним из источников таких методов является теория двойственности, результаты которой позволяют также производить экономический анализ оптимальных решений экономико-математи-ческих моделей.

Каждой задаче линейного программирования соответствует задача, называемая двойственной или сопряженной по отношению к исходной задаче. Теория двойственности оказалась полезной для проведения качественных исследований задач линейного программирования.

Экономическая интерпретация двойственной задачи.

Рассмотрим задачу об использовании ресурсов.

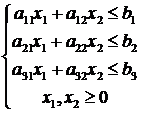
В этой модели: bi – запас ресурса Si, aij – число единиц ресурса Si, потребляемого при производстве единицы продукции Pj, Cj – прибыль (выручка от реализации).

Предположим, что некоторая организация решила закупить ресурсы S1, S2 и S3 предприятия и необходимо установить оптимальные цены на эти ресурсы: y1,y2 и y3.

Очевидно, что покупающая организация заинтересована в том, чтобы затраты на все ресурсы в количествах b1, b2, b3 по ценам y1,y2,y3 были минимальными, то есть

Z(y)= b1y1 + b2y2 + b3y3 → min.

С другой стороны, предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не менее той суммы, которую предприятие могло получить при переработке ресурсов в готовую продукцию. На изготовление продукции P1 расходуется a11 ресурса S1, a21 ресурса S2, а31 ресурса S3 a11y1 + a21y2 + a31y3 ≥ C1. Аналогично для продукции P2: a12y1 + a22y2 + a32y3 ≥ C2. Также необходимо учесть, что цены на ресурсы (объективно обусловленные оценки) не могут быть отрицательными.

Объединяя все вышесказанное, получаем следующую экономико-математическая модель двойственной задачи:

Z(y)=b1y1 + b2y2 + b3y3 → min

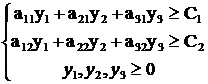
Цены ресурсов y1, y2, y3 называются учетными, неявными, теневыми. Смысл этих названий состоит в том, что это условные, “ненастоящие” цены. В отличие от “внешних” цен C1, C2 на продукцию, известных, как правило, до начала производства, цены ресурсов y1, y2, y3 являются внутренними, так как они задаются не извне, а определяются непосредственно в результате решения задачи, поэтому их часто называют оценками ресурсов.

Формулировка двойственной задачи

Найти такой набор оценок ресурсов, при которых общие затраты на ресурсы будут минимальными при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее выручки от реализации этой продукции.

Свойства взаимно двойственных задач

1.  В одной задаче ищут максимум целевой функции, а в другой минимум.

2.  Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений в другой.

3.  Каждая из задач задана в стандартной форме, причем в задаче на максимум все неравенства вида ”≤”, а в задаче на минимум – все неравенства вида “≥”.

4.  Матрицы коэффициентов при переменных в системах ограничений являются транспонированными друг к другу.

5.  Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.

6.  Условия неотрицательности переменных имеются в обеих задачах.

Пример решения задачи.

Составить двойственную задачу для заданной.

Дана целевая функция f(x)= –х1 + 2х2 → max

И система ограничений: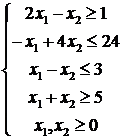

Приведем систему неравенств к правильному виду, чтобы все знаки неравенств соответствовали задаче на максимум:

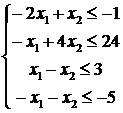
Тогда взаимно двойственная задача для исходной примет вид:

z(y)= – y1+24y2+3y3-5y4→min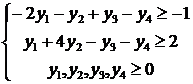

Запись решения двойственной задачи:

1) min z(y)=max f(x).

Если одна из задач имеет решение, то имеет решение и другая.

2) Установим соответствие между переменными: переменной xi из исходной задачи ставится в соответствие дополнительная переменная из двойственной задачи, введенная в i-е ограничение (x1 ~ y5, x2 ~ y6). Аналогично, первоначальным переменным двойственной задачи соответствуют дополнительные переменные исходной задачи.

3) Компоненты оптимального решения двойственной задачи равны по абсолютной величине коэффициентам при соответствующих переменных в последней записи целевой функции исходной задачи.

4) Если в одной из двойственных задач нарушается единственность оптимального решения, то оптимальное решение двойственной задачи вырожденное.

Ø  Важно помнить. Положительным (ненулевым) компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи. Таким образом, объективно обусловленные оценки ресурсов определяют степень дефицитности ресурсов: по оптимальному плану производства дефицитные (т. е. полностью использованные) ресурсы получают ненулевые оценки, а недефицитные – нулевые оценки.

Метод, при котором вначале симплексным методом решается двойственная задача, а затем оптимум и оптимальное решение исходной задачи находится с помощью теорем двойственности, называется двойственным симплексным методом. Его используют, когда решение двойственной задачи менее трудоемко (меньше число ограничений). Также с помощью решения двойственной задачи можно дать развернутую характеристику имеющимся на предприятии ресурсам и их использованию. Подробно об этом будет сказано позднее.

Пример решения задачи.. Последняя запись целевой функции исходной задачи с двумя переменными имела вид:

.

Ее решение .

Поставим в соответствие переменные:

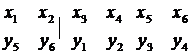
Под таблицей записываем по модулю коэффициенты из последней записи целевой функции исходной задачи.

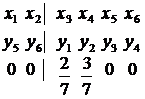
Следовательно, решение взаимно двойственной задачи будет иметь следующий вид: .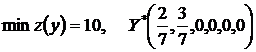

Чтобы лучше понять, почему дополнительные переменные одной задачи ставятся в соответствие первоначальным переменным другой задачи, представим их в виде таблицы, из которой видно, что они относятся к одинаковым экономическим понятиям.

Таблица 1.9

Ø  Важно помнить. Если линейная функция одной из взаимно двойственных не ограничена, то условия другой задачи противоречивы.

Объективно обусловленные оценки ресурсов имеют и другой экономический смысл:

1) Они равны значениям частных производных линейной функции по соответствующим аргументам, т. е.

.

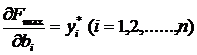Таким образом, оценки ресурсов показывают, на сколько денежных единиц изменится максимальная прибыль (выручка) от реализации продукции при изменении запаса соответствующего ресурса на одну единицу.

2) Двойственные оценки могут служить инструментом анализа и принятия правильных решений в условиях постоянно меняющегося производства. Так, например, с помощью объективно обусловленных оценок ресурсов возможно сопоставление оптимальных условных затрат и результатов производства.

Ø  Важно помнить. Оценки ресурсов позволяют судить об эффекте не любых, а лишь сравнительно небольших изменений ресурсов. При резких изменениях сами оценки могут стать другими, что приведет к невозможности их использования для анализа эффективности производства.

3) По соотношениям объективно обусловленных оценок могут быть определены расчетные нормы заменяемости ресурсов, при соблюдении которых проводимые замены в пределах устойчивости двойственных оценок не влияют на эффективность оптимального плана.

Задания для самостоятельной работы.

1.  Записать для задачи использования ресурсов взаимно двойственную и ее решение.

2.  Дана задача линейного программирования, ее решение и последняя запись целевой функции. Записать для нее двойственную задачу и ее решение.

Экономико-математическая модель задачи:

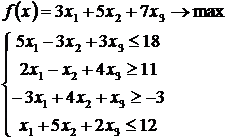
Последняя запись целевой функции: .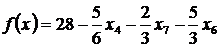

Ответ: .

3. Для производства изделий А и В предприятие использует три вида сырья. Все необходимые для решения задачи данные приведены в таблице.

Таблица 1.10

Затраты ресурсов на производство изделий и их запасы

Решить задачу симплексным методом, составить к ней двойственную задачу и записать ее решение. Объяснить экономический смысл переменных, ограничений и целевой функции обеих задач.

4. Используя геометрическое решение двойственной задачи и теоремы двойственности, решить задачу линейного программирования.

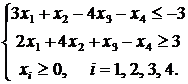
1.6. Транспортная задача

Важным частным случаем задачи линейного программирования является транспортная задача.

Пример решения задачи.

Построить экономико-математическую модель следующей задачи. Имеются 3 поставщика и 4 потребителя. Мощность поставщиков и спросы потребителей, а также затраты на перевозку единицы груза для каждой пары «поставщик – потребитель» сведены в таблицу поставок. В каждой клетке стоит коэффициент затрат – затраты на перевозку единицы груза от соответствующего поставщика к соответствующему потребителю.

Задача. Найти объем перевозок для каждой пары «поставщик – потребитель» так, чтобы:

1)  мощность всех поставщиков были реализованы;

2)  спросы всех потребителей удовлетворены;

3)  суммарные затраты на перевозку были минимальными.

Таблица 1.11

Транспортная задача

Составим экономико-математическую модель задачи.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9