Исследование операций в экономике (стр. 5 )

Таблица 1.21

Данные о стоимости перевозок,

мощностях поставщиков и спросе потребителей

Что означают следующие термины и понятия?

Теперь вы должны уметь:

o  составлять экономико-математические модели экономических задач;

o решать задачи линейного программирования графическим методом;

o решать задачи линейного программирования симплексным методом;

o решать задачи математического программирования методом Лагранжа;

o решать транспортные задачи;

o приводить любые транспортные задачи к сбалансированным;

o объяснять экономический смысл функции и ограничений в экономико-математических моделях задач;

o провести анализ использования ресурсов предприятия, используя теорию двойственности;

o приводить задачи к каноническому виду из стандартного и наоборот;

o анализировать результаты решения задач математического и линейного программирования;

o находить решение задачи, используя решение взаимно двойственной задачи.

Контрольные вопросы:

1.  Какие задачи называются задачами линейного программирования?

2.  Почему все переменные неотрицательные, как называются эти ограничения?

3.  Какое допустимое решение называется оптимальным?

4.  Чем отличаются каноническая и стандартная задачи линейного программирования?

5.  Геометрическое истолкование и свойства канонической задачи линейного программирования.

6.  Типы экономических задач, сводящихся к задачам линейного программирования.

7.  При решении задачи симплексным методом какой столбец называется ведущим, какая строка ведущей и какой элемент ведущим?

8.  Какой экономический смысл коэффициентов столбца Q? Почему при заполнении столбца Q делим только на положительные коэффициенты ведущего столбца?

9.  Почему решение считается найденным, если коэффициенты последней строки таблицы положительные?

10.  Какой экономический смысл имеют коэффициенты столбца свободных членов последней таблицы?

11.  Экономическая интерпретация двойственной задачи.

12.  Свойства взаимно двойственных задач.

13.  Экономический смысл транспортной задачи?

14.  Когда транспортная задача является задачей на избыток, а когда задачей на недостаток, как это исправить?

15.  В чем суть метода северо-западного угла?

16.  В чем суть метода минимальной стоимости?

17.  Когда опорный план считается оптимальным, то есть решение найдено?

18.  Какие типы экономических задач сводятся к транспортной задаче?

19.  Что показывают цифры в строке фиктивного поставщика и в столбце фиктивного потребителя, когда транспортная задача решена?

2. ТЕОРИЯ ИГР

Одним из важных разделов «Исследования операций» является теория игр, представляющая собой теоретические основы математических моделей принятия оптимальных решений в конфликтных ситуациях рыночных отношений, носящих характер конкурентной борьбы, в которых одна противоборствующая сторона выигрывает за счет проигрыша другой. Наряду с такой ситуацией в теории принятия решений также рассматривают так называемые ситуацию риска и ситуацию неопределенности, которые имеют различные модели и требуют разных критериев выбора оптимальных решений. В ситуации риска предполагаются известными не только возможные условия, в которых нужно принимать решение, но и вероятности их появления. В ситуации неопределенности вероятности условий неизвестны и нет никакой возможности получить о них дополнительную статистическую информацию. Окружающая решение задачи среда, которая проявляется в тех или иных условиях, называется природой, а соответствующие  математические модели называются играми с природой или теорией статистических решений.

Теория игр была систематически изложена ДЖ. Фон Нейманом и О. Монгерштерном в 1944 году. Они написали книгу, которая содержала главным образом экономические примеры, поскольку экономическому конфликту легче придать численную форму. Теория игр используется в области экономики и производства, бизнеса и финансов, сельского хозяйства и военного дела, биологии и социологии, психологии и политологии. К настоящему времени теория игр развилась в самостоятельную область математики и может рассматриваться независимо от ее приложений к реальным игровым ситуациям. По мнению лауреата Нобелевской премии по экономике за 1994 г. Нэша, теория игр вообще сыграла важную роль в интеллектуальной жизни ХХ века.

На практике часто приходится сталкиваться с задачами, в которых необходимо принимать решения в условиях неопределенности, то есть возникают ситуации, в которых две (или более) стороны преследуют различные цели, а результаты любого действия каждой из сторон зависят от мероприятий партнера. Такие ситуации, возникающие при игре в шахматы, шашки, домино, ситуации на рынке, когда выходит несколько производителей с одинаковым товаром (олигополия), покупатель и продавец, поставщик и потребитель, банк и клиент. То есть примером теории игр являются такие ситуации, в которых важную роль играют конфликты и совместные действия. Конфликт может возникнуть также из различия целей, которые отражают не только несовпадающие интересы различных сторон, но и многосторонние интересы одного и того же лица, например разработчик экономической политики обычно преследует разнообразные цели (рост объема производства, повышение доходов, снижение экологической нагрузки).

Таким образом, теория игр изучает и рассматривает методы определения оптимального поведения при управлении системами, в которых характерно наличие конфликтной ситуации (столкновение интересов). Для конфликтов характерно то, что ни один из его участников заранее не знает решений, принимаемых остальными участниками. Другими словами, участники конфликтов вынуждены действовать в условиях риска и неопределенности. Неопределенность исходов может проявляться не только в результате сознательных действий других участников, но и как результат действий тех или иных стихийных сил.

В свете «теории игр» можно рассмотреть экономику, общественные науки, бизнес и повседневную жизнь. К примеру, в экономике с точки зрения «теории игр» можно объяснить торговые и ценовые войны. Кроме того, некоторые обозреватели полагают, что, используя эту теорию, можно показать причины такого феномена, как «малоподвижные» цены. В соответствии с этой теорией фирмы заключают нечто вроде тайного соглашения о преобладающем значении цены (скажем, если речь идет об автомобильной или сталелитейной промышленности). После того как они пришли к соглашению, фирмы отказываются понижать или повышать цены, так как в противном случае участники рынка будут рассматривать такие изменения как сигнал объявления экономической войны. С помощью теории игр можно также объяснить, почему иностранная конкуренция может привести к более ожесточенной ценовой войне. Что случится, если японская фирма войдет на американский рынок, на котором уже существующие компании тайно договорились назначить высокую цену? Зарубежные фирмы могут «отказаться играть в эту игру». Они просто будут снижать цены в целях овладения большей долей рынка. Сговор может разрушиться.

Для грамотного решения задач с конфликтными ситуациями необходимы научно обоснованные методы. Такие методы разработаны математической теорией конфликтных ситуаций, которые носят название «теория игр».

Всякая претендующая на адекватность математическая модель социально-экономического явления должна отражать присущие ему черты конфликта, то есть описывать:

а) множество заинтересованных сторон, которые называются игроками;

б) возможные действия каждой из сторон, именуемые стратегиями или ходами;

в) интересы сторон, представленные функциями выигрыша (платежа) для каждого из игроков.

Сама модель конфликтной ситуации называется игрой.

2.1.  Классификация игр

Различные виды игр можно классифицировать, основываясь на том или ином принципе: по числу игроков, по числу стратегий, по свойствам функции выигрыша, по возможности предварительных переговоров и взаимодействия между игроками в ходе игры.

1)  Игра называется парной, если в ней участвуют два игрока, и множественной, если число игроков более двух.

2)  Игра называется с нулевой суммой или антагонистической, если выигрыш одного из игроков равен проигрышу другого. Игры с постоянной разностью – игроки выигрывают и проигрывают одновременно.

3)  Игра называется конечной, если у каждого игрока имеется конечное число стратегий, и бесконечной – в противном случае.

4)  Бескоалиционными называются игры, в которых игроки не имеют права вступать в соглашения, образовывать коалиции. В коалиционной игре, наоборот, игроки могут вступать в соглашения и образовывать коалиции. В кооперативной игре коалиции определены заранее, то есть до начала игры игроки могут принимать соглашения о своих стратегиях (возможность предварительных переговоров). В некооперативной игре игроки не могут координировать свои стратегии подобным образом и принимают решения независимо друг от друга.

5)  Комбинаторные игры: число исходов, стратегий, факторов конечное, не очень большое. Можно построить модель игры, выработать правила. Однако численное решение невозможно из-за большой размерности задачи. В случайных играх количество исходов не зависит от поведения игрока. В стратегических играх один участник находится в состоянии неопределенности относительно поведения других участников игры.

6)  Матричная игра – это конечная игра двух игроков с нулевой суммой, в которой задаются выигрыши первого игрока в виде матрицы. Любая матричная игра имеет решение и может быть реализована методами линейного программирования. Матричные игры еще называют играми в нормальной форме. Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой есть матрицы выигрышей (проигрышей) отдельно для каждого участника. Непрерывной считается игра, в которой функция выигрышей является непрерывной в зависимости от стратегий.

2.2. Другие термины и понятия

Выбор и осуществление одного из предусмотренных правилами действий называется ходом игрока. Ходы могут быть личными и случайными. Личный ход – это сознательный выбор игроком одного из возможных действий. Случайный ход – это случайно выбранное действие (выбор карты из перетасованной колоды).

Стратегией игрока называется совокупность правил, определяющих выбор действия при каждом ходе в зависимости от сложившейся ситуации. Чтобы решить игру или найти решение игры, следует для каждого игрока выбрать стратегию, которая удовлетворяет условию оптимальности, то есть один из игроков получает максимальный выигрыш, когда второй придерживается своей стратегии. В то же время второй игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии. Такие стратегии называются оптимальными.

Оптимальные стратегии должны удовлетворять условию устойчивости, то есть любому из игроков должно быть невыгодно отказываться от своей стратегии в этой игре. Если игра повторяется много раз, то игроков может интересовать не выигрыш и проигрыш в каждой конкретной партии, а средний выигрыш (проигрыш) во всех партиях.

Целью теории игр является определение оптимальной стратегии для каждого игрока.

Выигрыш – это мера эффекта для игрока. В теории игр выигрыш должен измеряться обязательно количественно.

В случае конечной игры двух лиц функции выигрыша каждого из игроков удобно представлять в виде матрицы выигрышей, где строки представляют собой стратегии одного игрока, а столбцы – стратегии другого. В клетках матрицы указываются выигрыши каждого из игроков в каждой из образующихся ситуаций. Данная форма представления конечных игр называется «матричные игры».

Пример решения задачи. Игра в «орлянку».

Если оба выбирают одинаковые стратегии (оба говорят “орел”), то 1-й выигрывает 1 рубль (а второй проигрывает); если выбирают разные, то 2-й выигрывает.

Таблица 2.1

Матрица выигрыша первого игрока (Н1)

Матрица выигрыша второго игрока (Н2)

Для антагонистических игр всегда Н1= – Н2.

Матрица, элементами которой являются выигрыши, соответствующие стратегиям игроков, называется платежной матрицей или матрицей игры.

Нижняя цена игры (α) (максиминный выигрыш – максимин) – это гарантированный выигрыш первого игрока при любой стратегии второго игрока (то есть из каждой строки выбираем минимальное число, а затем из всех этих минимумов берем наибольший). Стратегия, соответствующая максимину называется максиминной.

Верхняя цена игры (β) (минимаксный выигрыш – минимакс) – это гарантированный проигрыш второго игрока. (То есть из каждого столбца выбираем максимальное число, а затем из всех максимумов берем наименьший). Стратегия, соответствующая минимаксу, называется минимаксной.

Принцип, диктующий игрокам выбор наиболее «осторожных» минимаксной и максиминной стратегий, называется принципом минимакса. Этот принцип следует из разумного предположения, что каждый игрок стремится достичь цели, противоположной цели противника. Если верхняя и нижняя цены игры совпадают α=β=, то эта цена называется чистой ценой игры или ценой игры.

Для А=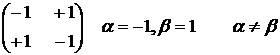

Для В=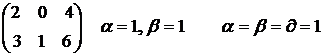

Минимаксные стратегии, соответствующие цене игры, являются оптимальными стратегиями или решением игры. То есть в этом случае первый игрок получает максимальный, не зависящий от поведения второго игрока выигрыш q, а второй игрок добивается минимального гарантированного, не зависящего от поведения первого игрока проигрыша q. Такое решение обладает устойчивостью, то есть если один из игроков придерживается своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной стратегии.

Пара стратегий дает оптимальное решение игры тогда и только тогда, когда соответствующий элемент матрицы (размер выигрыша-проигрыша) является одновременно наибольшим в своем столбце и наименьшим в своей строке. Такая ситуация, если она существует, называется седловой точкой. То есть игра разрешима в чистых стратегиях, каждый из игроков будет на каждом шаге выбирать одну и ту же стратегию и ему не выгодно от нее отклониться: если первый игрок выберет другую стратегию, у него будет выигрыш меньше, а если второй игрок выберет другую стратегию, у него проигрыш будет больше.

Пример решения задачи.

Определить верхнюю и нижнюю цену игры, заданной платежной матрицей. Имеет ли игра седловую точку?

Р=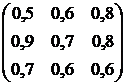

Таблица 2.2

Платежная матрица игры

– цена игры. Седловая точка (А2, В2).

Пример решения задачи. Рассмотрим две конкурирующие финансовые компании А и В. Компания В ведёт переговоры с организаторами каждого из трёх проектов В1 , В2 , В3 на предмет инвестирования. Задача компании В: положительный результат переговоров. Компания А ставит своей задачей свести переговоры компании В к отрицательному результату, с тем чтобы занять место компании В в инвестировании.

Компания А для достижения своей цели – срыва переговоров компании В – может применить одно из двух средств: А1 – предложить организаторам проектов более выгодные для них условия инвестирования по сравнению с компанией В и А2 – предоставить в распоряжение организаторов проектов материалы, компрометирующие компанию В.

Действие А1 компании А приводит к отрицательному результату переговоров компании В с организаторами проектов  В1 , В2 , В3,  соответственно, с вероятностями 0,7; 0,5; 0,3, а действие А2 – с вероятностями 0,6; 0,9; 0,4.

Решение. Смоделируем данную ситуацию. Поскольку компании А и В преследуют противоположные цели, то рассматриваемая конфликтная ситуация является антагонистической. Игроками являются финансовые компании А и В. Игрок А имеет две чистые стратегии А1 и А2: ; множество стратегий игрока В состоит из трёх стратегий: . Игрок В должен выбрать один из трех проектов, игрок А  выбирает одно из двух своих действий.

В качестве выигрыша игрока А (или проигрыша игрока В) рассмотрим вероятность отрицательного результата переговоров компании В. В соответствии со своими задачами игрок А стремится максимизировать выигрыш, а игрок В – минимизировать проигрыш.

Выясним, имеет ли игра седловую точку, то есть, разрешима ли игра в чистых стратегиях.

Матрица игры с показателями эффективности стратегий  А1 , А2  и показателями неэффективности стратегий В1 , В2 , В3 имеет следующий вид:

 Таблица 2.3

Платежная матрица игры

В данном случае максиминной стратегией игрока А является стратегия А2 , а минимаксной стратегией игрока В – стратегия В3.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9