Исследование операций в экономике (стр. 8 )

При определении временных параметров сетевой модели до сих пор предполагалось, что время выполнения каждой работы точно известно. На практике, чаще всего, продолжительность работы по сетевому графику заранее неизвестна и может принимать лишь одно из ряда возможных значений. То есть продолжительность работы t(i,j) является случайной величиной, характеризующейся своими числовыми характеристиками – средним значением (математическим ожиданием) и дисперсией 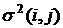. Для определения этих числовых характеристик на основании опроса ответственных исполнителей проекта и экспертов определяют три временные оценки:

a)  оптимистическую оценку , то есть продолжительность работы (i,j) при самых благоприятных условиях;

b)  пессимистическую оценку , то есть продолжительность работы (i,j) при самых неблагоприятных условиях;

c)  наиболее вероятную оценку , то есть продолжительность работы (i,j) при нормальных условиях.

На основании этих временных оценок вычисляем числовые характеристики:

, ,

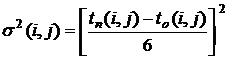или упрощенная (и менее точная) формула

.

Зная и , можно определить все временные параметры сетевого графика, так же как и в случае с фиксированными продолжительностями работ, но теперь эти параметры будут являться средними значениями соответствующих случайных величин. Поэтому предварительный анализ сетей со случайными продолжительностями работ, как правило, не ограничивается расчетами временных параметров. Очень важным моментом анализа становится оценка вероятности того, что срок выполнения проекта tкр не превзойдет заданного директивного срока Т.

,

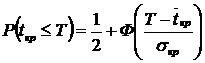где Ф(х) – функция Лапласа, ее значения табулированы, эта функция нечетная, то есть Ф(–х) = – Ф(х); – среднее квадратическое отклонение длины критического пути.

В некоторых случаях представляет интерес решение обратной задачи: определение максимального срока выполнения проекта Т, который возможен с заданной надежностью (вероятностью) β. В этом случае необходимо применить формулу

, где .

Пример решения задачи. Для заданного ранее сетевого графика определить вероятность того, что проект будет выполнен в срок Т = 63 суткам, если 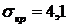. Оценить максимально возможный срок Т выполнения проекта с надежностью β=0,95.

,

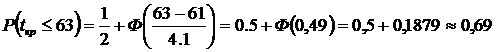то есть с вероятностью 0,69 проект будет выполнен за 63 дня.

Для обратной задачи:

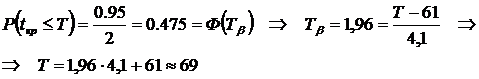
То есть с надежностью 0,95 срок выполнения проекта не превысит 69 суток.

,

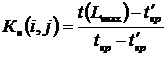где – продолжительность максимального пути, проходящего через работу (i,j);

– продолжительность (длина) критического пути;

– продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем.

Данную формулу можно привести к виду:

,

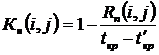где – полный резерв времени работы (i,j).

Ø  Важно помнить. Коэффициент напряженности может изменяться в пределах от 0 до 1.

Коэффициент напряженности равен 0 для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности, и равен 1 для работ критического пути.

Пример решения задачи. Для заданного ранее сетевого графика найти коэффициент напряженности работы (1,4) и работы (3,5).

Так как работа (3,5) лежит на критическом пути, то ее коэффициент напряженности равен 1: .

Коэффициент напряженности работы (1,4) вычислим двумя способами.

Ранее было установлено, что продолжительность критического пути равна 61 суткам. А максимальный путь, проходящий через работу (1,4), имеет следующую топологию: и продолжительность 49 суток. Этот путь совпадает с критическим на отрезке , продолжительность которого 32 суток. Подставляя эти значения в формулу, получим:

.

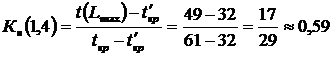По другой формуле полный резерв работы (1,4) равен 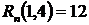, следовательно

.

То есть в обоих случаях результат, естественно, получился одинаковым.

Задание для самостоятельной работы.

Для заданного сетевого графика найти:

•  параметры событий (ранний срок свершения, поздний срок свершения и резерв времени);

•  параметры работ (ранний срок начала работы, поздний срок начала работы, ранний срок окончания работы и полный резерв времени);

•  вероятность того, что проект будет выполнен в срок, равный 27 суткам ;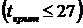

•  максимальный срок выполнения проекта с вероятностью 0,9;

•  коэффициент напряженности работы (4,5) и работы (3,7).

Дано, что .

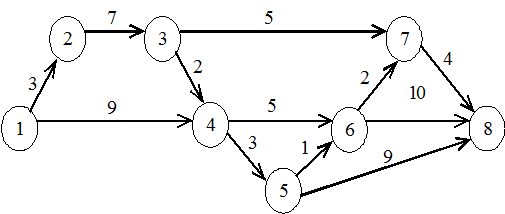
Рис. 3.3. Сетевой график

Оптимизация сетевого графика представляет процесс улучшения организации выполнения комплекса работ с учетом срока его выполнения. Оптимизация проводится с целью сокращения длины критического пути, выравнивания коэффициентов напряженности работ, рационального использования ресурсов.

В первую очередь принимаются меры по сокращению продолжи­тельности работ, находящихся на критическом пути. Это достигается:

• перераспределением всех видов ресурсов, как временных (использование резервов времени некритических путей), так и трудовых, материальных, энергетических (например, перевод части исполнителей, оборудования с некритических путей на работы критического пути); при этом перераспределение ресурсов должно идти, как правило, из зон, менее напряженных, в зоны, объединяющие наиболее напряженные работы;

• сокращением трудоемкости критических работ за счет передачи части работ на другие пути, имеющие резервы времени;

• параллельным выполнением работ критического пути; пересмотром топологии сети, изменением состава работ и структуры сети.

В процессе сокращения продолжительности работ критический путь может измениться. В дальнейшем процесс оптимизации будет направлен на сокращение продолжительности работ нового критического пути, и так будет продолжаться до получения удовлетворительного результата. В идеале длина любого из полных путей может стать равной длине критического пути или, по крайней мере, пути критической зоны. Тогда все работы будут вестись с равным напряжением, а срок завершения проекта существенно сократится.

Весьма эффективным является использование метода стати­стического моделирования, основанного на многократных последо­вательных изменениях продолжительности работ (в заданных пределах) и "проигрывании" на компьютере различных вариантов сетевого графика с расчетами всех его временных параметров и коэффициентов напряженности работ. Процесс «проигрывания» продолжается до тех пор, пока не будет получен приемлемый вариант плана или пока не будет установлено, что все имеющиеся возможности улучшения плана исчерпаны и поставленные перед разработчиком проекта условия невыполнимы.

На практике при попытках эффективного улучшения составленного плана неизбежно введение дополнительно к оценкам сроков фак­тора стоимости работ.

Оптимизация сетевого графика в зависимости от полноты ре­шаемых задач может быть условно разделена на частную и ком­плексную. Видами частной оптимизации сетевого графика явля­ются: минимизация времени выполнения комплекса работ при заданной его стоимости; минимизация стоимости комплекса работ при заданном времени выполнения проекта. Комплексная оптимизация представляет собой нахождение оптимального соотношения величин стоимости и сроков выполнения проекта в зависимости от конкретных целей, ставящихся при его реализации.

При линейной зависимости стоимости работ от их продолжительности задача построения оптимально сетевого графика может быть сформулирована как задача линейного программирования, в которой необходимо минимизировать стоимость выполнения проекта при двух группах ограничений. Первая группа ограничений показывает, что продолжительность каждой работы должна находиться в указанных пределах. Вторая группа ограничений требует, чтобы продолжительность любого полного пути сетевого графика не превышала установленного директивного срока выполнения проекта.

Задание для самостоятельной работы.

Фирма может влиять дополнительным финансированием на скорость строительства своего торгового павильона. Очередность выполнения работ, их нормальная и ускоренная продолжительность выполнения, а также стоимость строительно-монтажных работ при нормальном и ускоренном режиме их выполнения приведены в следующей таблице.

Таблица 3.3

Условие задачи

Требуется:

1.  С учетом технологической последовательности работ построить сетевой график выполнения этих работ.

2.  Рассчитать временные характеристики сетевого графика при нормальном режиме выполнения работ.

3.  Найти все критические пути и их продолжительность, определить стоимость всего комплекса работ.

4.  Указать стратегию минимального удорожания комплекса работ при сокращении сроков строительства на 4 дня. В какую итоговую сумму обойдется фирме ускоренная стройка павильона?

Что означают следующие термины и понятия?

Теперь вы должны уметь:

o  с учетом технологической последовательности работ строить сетевой график выполнения этих работ;

o рассчитывать временные характеристики сетевого графика (событий и работ);

o находить критические пути и их продолжительность;

o определять стратегию минимального удорожания комплекса работ при сокращении сроков;

o определять коэффициенты напряженности работ;

o оценивать вероятность того, что срок выполнения проекта tкр не превзойдет заданного директивного срока Т;

o определять максимальный срок выполнения проекта Т, который возможен с заданной надежностью (вероятностью) β.

Контрольные вопросы:

1.  Основные элементы сетевой модели.

2.  Правила построения сетевых графиков.

3.  Понятие ранга события.

4.  Временные параметры событий.

5.  Временные параметры работ.

6.  Сетевое планирование в условиях неопределенности.

7.  Коэффициент напряженности работы: что показывает и как определяется?

8.  В чем суть оптимизации сетевого графика?

4. Системы массового обслуживания

4.1. Структура и классификация систем массового обслуживания

Нередко возникает необходимость в решении вероятностных задач, связанных с системами массового обслуживания (СМО), примерами которых могут быть:

•  Билетные кассы;

•  Ремонтные мастерские;

•  Торговые, транспортные, энергетические системы;

•  Системы связи;

•  и т. д.

Общность таких систем выявляется в единстве математических методов и моделей, применяемых при исследовании их деятельности.

Рис. 4.1. Основные сферы применения ТМО

На вход в СМО поступает поток требований на обслуживание. Например, клиенты или пациенты, поломки в оборудовании, телефонные вызовы. Требования поступают нерегулярно, в случайные моменты времени. Случайный характер носит и продолжительность обслуживания. Это создает нерегулярность в работе СМО, служит причиной ее перегрузок и недогрузок.

Системы массового обслуживания обладают различной структурой, но обычно в них можно выделить четыре основных элемента:

1.  Входящий поток требований.

2.  Накопитель (очередь).

3.  Приборы (каналы обслуживания).

4.  Выходящий поток.

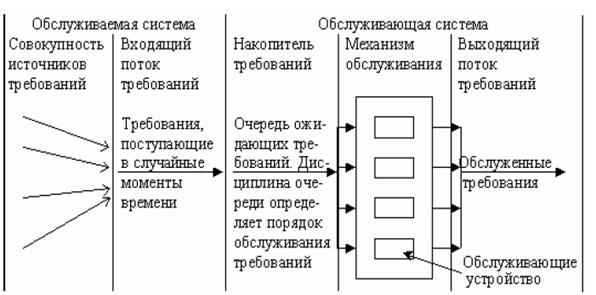
Рис. 4.2. Общая схема систем массового обслуживания

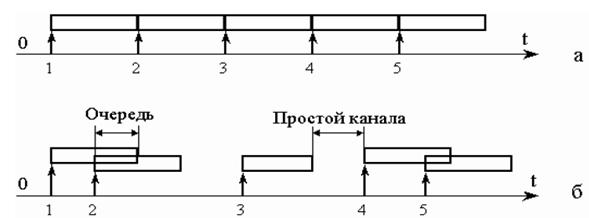
Рис. 4.3. Модель работы системы

(стрелками показаны моменты поступления требований в

систему, прямоугольниками – время обслуживания)

На рис.4.3 а представлена модель работы системы с регулярным потоком требований. Поскольку известен промежуток между поступлениями требований, то время обслуживания выбрано так, чтобы полностью загрузить систему. Для системы со стохастическим потоком требований ситуация совершенно иная – требования приходят в различные моменты времени и время обслуживания тоже является случайной величиной, которое может быть описано неким законом распределения (рис.4.3 б).

В зависимости от правил образования очереди различают следующие СМО:

1)  системы с отказами, в которых при занятости всех каналов обслуживания заявка покидает систему необслуженной;

2)  системы с неограниченной очередью, в которых заявка встает в очередь, если в момент ее поступления все каналы обслуживания были заняты;

3)  системы с ожиданием и ограниченной очередью, в которых время ожидания ограниченно какими-либо условиями или существуют ограничения на число заявок, стоящих в очереди.

Рассмотрим характеристики входящего потока требований.

Поток требований называется стационарным, если вероятность попадания того или иного числа событий на участок времени определенной длины зависит только от длины этого участка.

Поток событий называется потоком без последствий, если число событий, попадающих на некоторый участок времени, не зависит от числа событий, попадающих на другие.

Поток событий называется ординарным, если невозможно одновременное поступление двух или более событий.

Поток требований называется пуассоновским (или простейшим), если он обладает тремя свойствами: стационарен, ординарен и не имеет последствий. Название связано с тем, что при выполнении указанных условий число событий, попадающих на любой фиксированный интервал времени, будет распределен по закону Пуассона.

Интенсивностью потока заявок λ называется среднее число заявок, поступающих из потока за единицу времени.

Для стационарного потока интенсивность постоянна. Если τ – среднее значение интервала времени между двумя соседними заявками, то В случае пуассоновского потока вероятность поступления на обслуживание m заявок за промежуток времени t определяется по закону Пуассона:

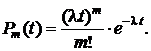
Время между соседними заявками распределено по экспоненциальному закону с плотностью вероятности

Время обслуживания является случайной величиной и подчиняется показательному закону распределения с плотностью вероятности где μ – интенсивность потока обслуживания, т. е. среднее число заявок, обслуживаемых в единицу времени,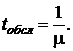

Отношение интенсивности входящего потока к интенсивности потока обслуживания называется загрузкой системы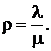

Загрузка – это среднее число заявок, приходящих за среднее время обслуживания одной заявки.

4.2.  Марковский процесс

Система массового обслуживания представляет собой систему дискретного типа с конечным или счетным множеством состояний, а переход системы из одного состояния в другое происходит скачком, когда осуществляется какое-нибудь событие.

Процесс называется процессом с дискретными состояниями, если его возможные состояния можно заранее перенумеровать, и переход системы из состояния в состояние происходит практически мгновенно.

Такие процессы бывают двух типов: с дискретным или непрерывным временем.

В случае дискретного времени переходы из состояния в состояние могут происходить в строго определенные моменты времени. Процессы с непрерывным временем отличаются тем, что переход системы в новое состояние возможен в любой момент времени.

Случайным процессом называется соответствие, при котором каждому значению аргумента (в данном случае – моменту из промежутка времени проводимого опыта) ставится в соответствие случайная величина (в данном случае – состояние СМО). Случайной величиной называется величина, которая в результате опыта может принять одно, но неизвестное заранее, какое именно, числовое значение из данного числового множества.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9