Поэтому для решения задач теории массового обслуживания необходимо этот случайный процесс изучить, т. е. построить и проанализировать его математическую модель.
Случайный процесс называется марковским, если для любого момента времени ![]() вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент
вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент ![]() и не зависят от того, когда и как система пришла в это состояние.
и не зависят от того, когда и как система пришла в это состояние.
Переходы системы из состояния в состояние происходит под действием каких-то потоков (поток заявок, поток отказов). Если все потоки событий, приводящие систему в новое состояние, – простейшие пуассоновские, то процесс, протекающий в системе, будет марковским, так как простейший поток не обладает последствием: в нем будущее не зависит от прошлого.
Пример марковского процесса: система ![]() – счетчик в такси. Состояние системы в момент
– счетчик в такси. Состояние системы в момент ![]() характеризуется числом километров (десятых долей километров), пройденных автомобилем до данного момента. Пусть в момент
характеризуется числом километров (десятых долей километров), пройденных автомобилем до данного момента. Пусть в момент ![]() счетчик показывает
счетчик показывает ![]() . Вероятность того, что в момент
. Вероятность того, что в момент ![]() счетчик покажет то или иное число километров (точнее, соответствующее число рублей)
счетчик покажет то или иное число километров (точнее, соответствующее число рублей) ![]() , зависит от
, зависит от ![]() , но не зависит от того, в какие моменты времени изменялись показания счетчика до момента
, но не зависит от того, в какие моменты времени изменялись показания счетчика до момента ![]() .
.
Многие процессы можно приближенно считать марковскими. Например, процесс игры в шахматы: система ![]() – группа шахматных фигур. Состояние системы характеризуется числом фигур противника, сохранившихся на доске в момент
– группа шахматных фигур. Состояние системы характеризуется числом фигур противника, сохранившихся на доске в момент ![]() . Вероятность того, что в момент
. Вероятность того, что в момент ![]() материальный перевес будет на стороне одного из противников, зависит в первую очередь от того, в каком состоянии находится система в данный момент
материальный перевес будет на стороне одного из противников, зависит в первую очередь от того, в каком состоянии находится система в данный момент ![]() , а не от того, когда и в какой последовательности исчезли фигуры с доски до момента
, а не от того, когда и в какой последовательности исчезли фигуры с доски до момента ![]() .
.
4.3. Системы массового обслуживания с отказами
В системах с отказами заявка, поступившая в момент, когда все каналы обслуживания заняты, немедленно получает отказ, покидает систему и в дальнейшем в процессе обслуживания не участвует.
Имеется n каналов в обслуживании, на которые поступает поток заявок с интенсивностью λ. Поток обслуживания имеет интенсивность μ (величина, обратная среднему времени обслуживания ![]() ). Требуется найти вероятности состояний СМО и характеристики ее эффективности.
). Требуется найти вероятности состояний СМО и характеристики ее эффективности.
Так как оба потока – заявок и освобождений – простейшие, процесс, протекающий в системе, будет марковским. Рассмотрим ее как систему с конечным множеством состояний:
![]() свободны все каналы;
свободны все каналы;
![]() занят ровно один канал;
занят ровно один канал;
…
![]() заняты k каналов;
заняты k каналов;
…
![]() заняты все n каналов/
заняты все n каналов/
Через ![]() обозначим вероятность того, что в момент времени t система будет находиться в состоянии
обозначим вероятность того, что в момент времени t система будет находиться в состоянии ![]() .
.
Простейшие задачи для систем массового обслуживания с отказами были впервые решены . Им же были выведены формулы оценки функционирования этих систем при условии поступления простейшего потока заявок и для показательного закона распределения времени обслуживания.
Для установившегося процесса обслуживания при этих условиях Эрланг получил следующие зависимости.
· Вероятность того, что обслуживанием заняты k аппаратов (линий, приборов и т. п.):
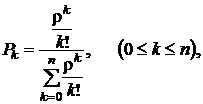 (4.1)
(4.1)
где 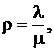 k – количество занятых аппаратов,
k – количество занятых аппаратов,
λ – интенсивность потока заявок,
μ – интенсивность потока обслуживания.
Частные случаи:
· Вероятность простоя (того, что все обслуживающие аппараты свободны, нет заявок):
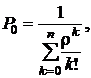 (4.2)
(4.2)
· Вероятность отказа (вероятность того, что все обслуживающие приборы заняты):
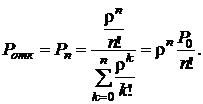 (4.3)
(4.3)
Отсюда находим относительную пропускную способность, т. е. среднюю долю пришедших заявок, обслуживаемых системой, – вероятность того, что заявка будет обслужена:
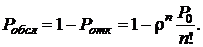 (4.4)
(4.4)
Абсолютную пропускную способность, т. е. среднее число заявок, обслуживаемых в единицу времени, получим, умножив интенсивность потока заявок на относительную пропускную способность:
![]()
Абсолютная пропускная способность – это интенсивность потока обслуженных системой заявок, а каждый занятый канал в единицу времени обслуживает в среднем μ заявок. Значит, среднее число занятых каналов равно
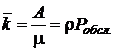 (4.5)
(4.5)
Доля каналов, занятых обслуживанием (коэффициент загрузки):
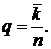 (4.6)
(4.6)
Пример решения задачи.
На вход трехканальной СМО с отказами поступает поток заявок с интенсивностью λ = 4 заявки в минуту. Время обслуживания заявки одним каналом 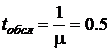 мин.
мин.
Найти показатели эффективности работы системы.
Решение.
Находим вероятность простоя трехканальной СМО по формуле (4.2):
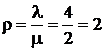 - загрузка системы (среднее число заявок, приходящих за среднее время обслуживания одной заявки).
- загрузка системы (среднее число заявок, приходящих за среднее время обслуживания одной заявки).
![]()
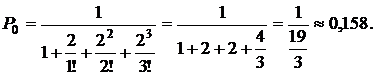
Вероятность отказа определяем по формуле (4.3):
![]()
Относительная пропускная способность системы:
![]()
Абсолютная пропускная способность системы (среднее число заявок, обслуживаемых в единицу времени):
![]()
Среднее число занятых каналов (в ед. времени) определяем по формуле (4.5):
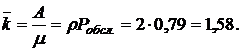
Доля каналов, занятых обслуживанием (формула (4.6)):
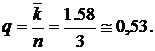
Среднее время пребывания заявки в СМО находим как вероятность того, что заявка принимается к обслуживанию, умноженную на среднее время обслуживания:
![]() мин.
мин.
4.4. Системы массового обслуживания
с неограниченным ожиданием
Пусть имеется n-канальная СМО с очередью, на которую не наложено ограничений ни по длине очереди, ни по времени ожидания. В силу неограниченности очереди каждая заявка рано или поздно будет обслужена, поэтому
![]()
![]()
Для СМО с неограниченной очередью накладывается ограничение ![]() .
.
Если это условие нарушено, то очередь растет до бесконечности, наступает явление «взрыва».
· Вероятность простоя (того, что все обслуживающие аппараты свободны, нет заявок):
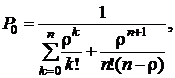 (4.7)
(4.7)
· Вероятность занятости обслуживанием k каналов:
![]() (4.8)
(4.8)
· Вероятность занятости обслуживанием всех каналов при отсутствии очереди:
![]() (4.9)
(4.9)
· Вероятность наличия очереди есть вероятность того, что число требований в системе больше числа каналов:
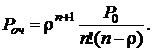 (4.10)
(4.10)
· Вероятность для заявки попасть в очередь есть вероятность занятости всех каналов, эта вероятность равна сумме вероятностей наличия очереди и занятости всех n каналов при отсутствии очереди:
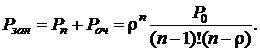 (4.11)
(4.11)
· Среднее число занятых обслуживанием каналов:
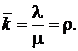 (4.12)
(4.12)
· Доля каналов, занятых обслуживанием:
![]() (4.13)
(4.13)
· Среднее число заявок в очереди (длина очереди)
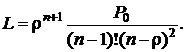 (4.14)
(4.14)
· Среднее число заявок в системе
![]() (4.15)
(4.15)
· Среднее время ожидания заявки в очереди
![]() (4.16)
(4.16)
· Среднее время пребывания заявки в системе
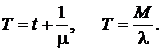 (4.17)
(4.17)
Пример решения задачи.
На вход трехканальной СМО с неограниченной очередью поступает поток заявок с интенсивностью λ = 4 заявки в минуту. Среднее время обслуживания заявки 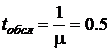 ч.
ч.
Найти показатели эффективности работы системы.
Решение
Для рассматриваемой системы
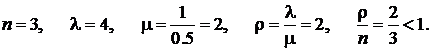
Определяем вероятность простоя по формуле (4.7):
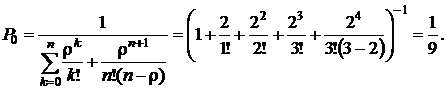
Среднее число заявок в очереди находим по формуле (4.14):
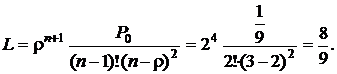
Среднее время ожидания заявки в очереди считаем по формуле (4.16):
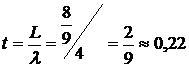 ч.
ч.
Среднее время пребывания заявки в системе
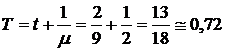 ч.
ч.
4.5. Системы массового обслуживания
с ожиданием и ограниченной длинной очереди
Имеется n-канальная СМО с ожиданием, в которой количество заявок, стоящих в очереди, ограничено числом m, т. е. заявка, заставшая все каналы занятыми, становится в очередь, только если в ней находится менее m заявок.
Если число заявок в очереди равно m, то последняя прибывшая заявка в очередь не становится и покидает систему необслуженной.
Системы с ограниченной очередью являются обобщением двух рассмотренных ранее СМО: при m = 0 получаем СМО с отказами, при m = ¥ получаем СМО с ожиданием.
· Вероятность простоя (того, что все обслуживающие аппараты свободны, нет заявок):
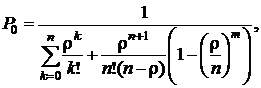 (4.18)
(4.18)
· Вероятность отказа в обслуживании равна вероятности ![]() того, что в очереди уже стоят m заявок:
того, что в очереди уже стоят m заявок:
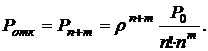 (4.19)
(4.19)
· Относительная пропускная способность есть величина, дополняющая вероятность отказа до 1, т. е. вероятность обслуживания:
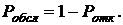
(4.20)
· Абсолютная пропускная способность определяется равенством:
![]() (4.21)
(4.21)
· Среднее число занятых обслуживанием каналов:
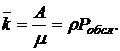 (4.22)
(4.22)
· Среднее число заявок в очереди (средняя длина очереди)
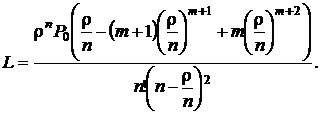 (4.23)
(4.23)
· Среднее время ожидания обслуживания в очереди
![]() (4.24)
(4.24)
· Среднее число заявок в системе
![]() (4.25)
(4.25)
· Среднее время пребывания заявки в системе
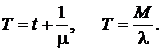 (4.26)
(4.26)
Пример решения задачи.
В парикмахерской работают 3 мастера, в зале ожидания расположено 3 стула. Поток клиентов имеет интенсивность λ = 12 клиентов в час. Среднее время обслуживания заявки 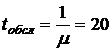 мин. Определить относительную и абсолютную пропускную способность системы, среднее число занятых кресел, среднюю длину очереди, среднее время, которое клиент проводит в парикмахерской.
мин. Определить относительную и абсолютную пропускную способность системы, среднее число занятых кресел, среднюю длину очереди, среднее время, которое клиент проводит в парикмахерской.
Решение
Для данной задачи
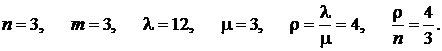
Определяем вероятность простоя по формуле (4.18):
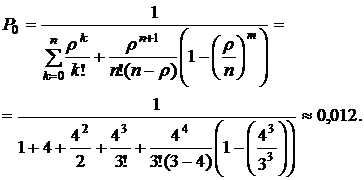
Вероятность отказа в обслуживании определим по формуле (4.19)
![]()
Относительная пропускная способность, т. е. вероятность обслуживания:
![]()
Абсолютная пропускная способность (среднее число заявок, обслуживаемых в единицу времени):
![]()
Среднее число занятых обслуживанием каналов (парикмахеров):
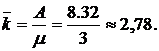
Среднее число заявок в очереди (средняя длина очереди)
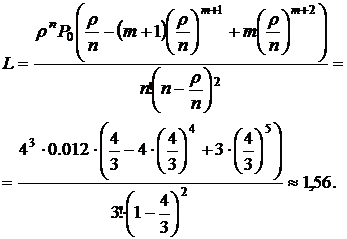
Среднее время ожидания обслуживания в очереди
![]() ч.
ч.
Среднее число заявок в системе
![]() .
.
Среднее время пребывания заявки в системе
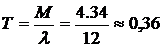 ч.
ч.
4.6. Замкнутые системы массового обслуживания
До сих пор мы рассматривали системы, в которых входящий поток никак не связан с выходящим. Такие системы называются разомкнутыми. В некоторых же случаях обслуженные требования после задержки опять поступают на вход. Такие СМО называются замкнутыми.
Примеры:
· Поликлиника, обслуживающая данную территорию.
· Бригада рабочих, закрепленная за группой станков.
В замкнутых СМО циркулирует одно и то же конечное число потенциальных требований. Пока потенциальное требование не реализовалось в качестве требования на обслуживание, считается, что оно находится в блоке задержки.
В момент реализации оно поступает в саму систему. Например, рабочие обслуживают группу станков. Каждый станок является потенциальным требованием, превращаясь в реальное в момент своей поломки. Пока станок работает, он находится в блоке задержки, а с момента поломки до момента окончания ремонта – в самой системе. Каждый работник является каналом обслуживания.
Пусть n – число каналов обслуживания, s – число потенциальных заявок, ![]() , λ –интенсивность потока заявок каждого потенциального требования, m – интенсивность обслуживания,
, λ –интенсивность потока заявок каждого потенциального требования, m – интенсивность обслуживания, 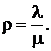 . Поток
. Поток
· Вероятность простоя (того, что все обслуживающие аппараты свободны, нет заявок):
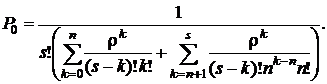 (4.27)
(4.27)
· Финальные вероятности состояний системы
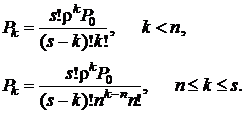 (4.28)
(4.28)
Через эти вероятности выражается среднее число замкнутых каналов:
![]() или
или
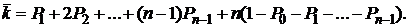 (4.29)
(4.29)
Через ![]() находим абсолютную пропускную способность системы
находим абсолютную пропускную способность системы
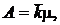 (4.30)
(4.30)
а также среднее число заявок в системе
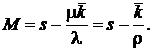 (4.31)
(4.31)
Пример решения задачи.
Рабочий обслуживает 4 станка. Каждый станок отказывает с интенсивностью λ = 0,5 отказа в час. Среднее время ремонта 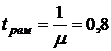 ч. Определить пропускную способность системы.
ч. Определить пропускную способность системы.
Решение
Эта задача рассматривает замкнутую СМО,
![]()
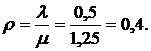
Вероятность простоя рабочего определяется по формуле (4.27):
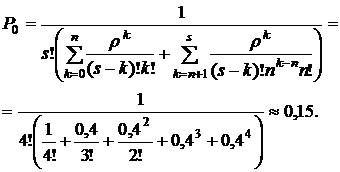
Вероятность занятости рабочего
![]() .
.
Если рабочий занят, он налаживает ![]() станков в единицу времени, пропускная способность системы
станков в единицу времени, пропускная способность системы
![]() станков в час.
станков в час.
Ø Важно помнить. При применении экономического показателя важно правильно оценить реальные издержки, которые могут изменяться, например, от времени года, от объема запасов угля и пр.
На практике часто встречаются; замкнутые системы обслуживания, у которых входящий поток заявок существенным образом зависит от состояния самой СМО. В качестве примера можно привести ситуацию, когда на ремонтную базу поступают с мест эксплуатации некоторые машины: понятно, что чем больше машин находится в состоянии ремонта, тем меньше их продолжает эксплуатироваться и тем меньше интенсивность потока вновь поступающих на ремонт машин. Для замкнутых СМО характерным является ограниченное число источников заявок, причем каждый источник «блокируется» на время обслуживания его заявки (т. е. он не выдает новых заявок). В подобных системах при конечном числе состояний СМО предельные вероятности будут существовать при любых значения интенсивностей потоков заявок и обслуживании. Они могут быть вычислены, если вновь обратиться к процессу гибели и размножения.
Задания для самостоятельной работы.
1. Станция «Железная дорога» в мегаполисе принимает составы для разгрузки угля на ![]() платформах. В среднем за сутки на станцию прибывают 16 составов с углем. Поступление носит случайный характер. Плотность прихода составов показала, что поступление на разгрузку удовлетворяет пуассоновскому потоку с параметром
платформах. В среднем за сутки на станцию прибывают 16 составов с углем. Поступление носит случайный характер. Плотность прихода составов показала, что поступление на разгрузку удовлетворяет пуассоновскому потоку с параметром  состава в час. Время разгрузки состава является случайной величиной, удовлетворяющей экспоненциальному закону со средним временем разгрузки
состава в час. Время разгрузки состава является случайной величиной, удовлетворяющей экспоненциальному закону со средним временем разгрузки 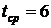 час. Простой состава в сутки составляет
час. Простой состава в сутки составляет ![]() y. e; простой платформы в сутки за опоздание прихода состава –
y. e; простой платформы в сутки за опоздание прихода состава – ![]() y. e; стоимость эксплуатации платформы в сутки –
y. e; стоимость эксплуатации платформы в сутки – 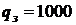 y. e. Издержки подсчитать за сутки. Требуется провести анализ эффективности функционирования станции.
y. e. Издержки подсчитать за сутки. Требуется провести анализ эффективности функционирования станции.
2. Интернет-провайдер в небольшом городе имеет 5 выделенных каналов обслуживания. В среднем на обслуживание одного клиента уходит 25 минут. В систему в среднем поступает 6 заказов в час. Если свободных каналов нет, следует отказ. Определить характеристики обслуживания: вероятность отказа, среднее число занятых обслуживанием линий связи, абсолютную и относительную пропускные способности, вероятность обслуживания. Найти число выделенных каналов, при котором относительная пропускная способность системы будет не менее 0,95. Считать, что потоки заявок и обслуживаний простейшие.
3. Порт имеет один причал для разгрузки судов. Интенсивность потока 0,4 в сутки, среднее время разгрузки одного судна 2 суток. В предположении неограниченности очереди определить показатели эффективности работы причала и вероятность ожидания разгрузки не более 2 судов.
4. Порт имеет один причал для разгрузки судов. Интенсивность потока 0,4 в сутки, среднее время разгрузки одного судна 2 суток. Определить показатели работы порта при условии, что судно покидает порт при наличии в очереди более 3 судов.
Что означают следующие термины и понятия?
СМО | Марковский процесс |
Очередь | Абсолютная пропускная способность |
Системы с неограниченной очередью Каналы обслуживания | Относительная пропускная способность Среднее число занятых каналов |
Системы с отказами Системы с ожиданием и ограниченной очередью | Вероятность простоя Среднее время пребывания заявки в СМО |
Поток требований | Вероятность отказа |
Стационарный поток Поток без последействий | Вероятность отказа Среднее число заявок |
Ординарный поток | Среднее время ожидания |
Пуассоновский поток | Замкнутые СМО |
Интенсивность потока | Разомкнутые СМО |
Загрузка системы |
Теперь вы должны уметь:
o при решении прикладных задач использовать основы марковской теории;
o использовать методы статистического моделирования систем массового обслуживания;
o определить параметры систем массового обслуживания с отказами, с ограниченной очередью, с неограниченной очередью;
o описывать функционирование различных систем массового обслуживания;
o строить математические модели массового обслуживания;
o определять основные характеристики функционирования различных систем массового обслуживания.
Контрольные вопросы:
1. Дайте определение системы массового обслуживания с неограниченной очередью.
2. Определите процесс функционирования системы массового обслуживания с неограниченной очередью.
3. Перечислите основные характеристики системы массового обслуживания с неограниченной очередью.
4. Дайте определение системы массового обслуживания с отказами.
5. Определите процесс функционирования системы массового обслуживания с отказами.
6. Перечислите основные характеристики системы массового обслуживания с отказами.
7. Дайте определение системы массового обслуживания с ограниченной очередью.
8. Определите процесс функционирования системы массового обслуживания с ограниченной очередью.
9. Перечислите основные характеристики системы массового обслуживания с ограниченной очередью.
10. В чем особенности замкнутых систем массового обслуживания?
список ЛИТЕРАТУРЫ
1. Акулич программирование в примерах и задачах. – М.: Высшая школа. 1986.
2. , Бережной методы моделирования экономических систем. – М.: Финансы и статистика. 2001. – 368 с.
3. Гнеденко, в теорию массового обслуживания /, : 3-е изд., испр. и доп. – М.: Эдиториал УРСС, 2005. – 400 с.
4. , , Черемных методы в экономике. – М.: ДИС, 1997.
5. Исследование операций в экономике / под ред. М.: Банки и биржи, изд-кое объединение ЮНИТИ, 2000.
6. Количественные методы финансового анализа / под ред. Стивена Дж. Брауна и Крицмена. – М.: ИНФРА-М, 1996.
7. , Чупрынов математики и ее приложения в экономическом образовании. – М.: ДЕЛО, 2000.
8. , Путко : учебник для вузов / под ред. проф. . – М.: ЮНИТИ-ДАНА, 2002. – 311с.
9. , Бабешко методы в управлении экономикой и бизнесом. – М.: ДЕЛО, 2001. – 464 с.
10. , , Брайлов в экономике. – М.: Финансы и статистика, 1999.
11. Шелобаев методы и модели. Экономика, финансы, бизнес: учебное пособие для вузов. – М.: ЮНИТИ-ДАНА, 2000. – 367 с.
12. Экономико-математические методы и прикладные модели: учебное пособие для вузов // , , и др.; Под ред. . – М.: ЮНИТИ, 1999. – 391 с.
13. Экономический анализ: ситуации, тесты, примеры, задачи, выбор оптимальных решений, финансовое прогнозирование / под ред. проф. и проф. – М.: Финансы и статистика, 2000.
Приложение
Таблица значений функции Лапласса
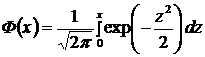
x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
0.00 | 0.0000 | 0.32 | 0.1255 | 0.64 | 0.2389 | 0.96 | 0.3315 |
0.01 | 0.0040 | 0.33 | 0.1293 | 0.65 | 0.2422 | 0.97 | 0.3340 |
0.02 | 0.0080 | 0.34 | 0.1331 | 0.66 | 0.2454 | 0.98 | 0.3365 |
0.03 | 0.0120 | 0.35 | 0.1368 | 0.67 | 0.2486 | 0.99 | 0.3389 |
0.04 | 0.0160 | 0.36 | 0.1406 | 0.68 | 0.2517 | 1.00 | 0.3413 |
0.05 | 0.0199 | 0.37 | 0.1443 | 0.69 | 0.2549 | 1.01 | 0.3438 |
0.06 | 0.0239 | 0.38 | 0.1480 | 0.70 | 0.2580 | 1.02 | 0.3461 |
0.07 | 0.0279 | 0.39 | 0.1517 | 0.71 | 0.2611 | 1.03 | 0.3485 |
0.08 | 0.0319 | 0.40 | 0.1554 | 0.72 | 0.2642 | 1.04 | 0.3508 |
0.09 | 0.0359 | 0.41 | 0.1591 | 0.73 | 0.2673 | 1.05 | 0.3531 |
0.10 | 0.0398 | 0.42 | 0.1628 | 0.74 | 0.2703 | 1.06 | 0.3554 |
0.11 | 0.0438 | 0.43 | 0.1664 | 0.75 | 0.2734 | 1.07 | 0.3577 |
0.12 | 0.0478 | 0.44 | 0.1700 | 0.76 | 0.2764 | 1.08 | 0.3599 |
0.13 | 0.0517 | 0.45 | 0.1736 | 0.77 | 0.2794 | 1.09 | 0.3621 |
0.14 | 0.0557 | 0.46 | 0.1772 | 0.78 | 0.2823 | 1.10 | 0.3643 |
0.15 | 0.0596 | 0.47 | 0.1808 | 0.79 | 0.2852 | 1.11 | 0.3665 |
0.16 | 0.0636 | 0.48 | 0.1844 | 0.80 | 0.2881 | 1.12 | 0.3686 |
0.17 | 0.0675 | 0.49 | 0.1879 | 0.81 | 0.2910 | 1.13 | 0.3708. |
0.18 | 0.0714 | 0.50 | 0.1915 | 0.82 | 0.2939 | 1.14 | 0.3729 |
0.19 | 0.0753 | 0.51 | 0.1950 | 0.83 | 0.2967 | 1.15 | 0.3749 |
0.20 | 0.0793 | 0.52 | 0.1985 | 0.84 | 0.2995 | 1.16 | 0.3770 |
0.21 | 0.0832 | 0.53 | 0.2019 | 0.85 | 0.3023 | 1.17 | 0.3790 |
0.22 | 0.0871 | 0.54 | 0.2054 | 0.86 | 0.3051 | 1.18 | 0.3810 |
0.23 | 0.0910 | 0.55 | 0.2088 | 0.87 | 0.3078 | 1.19 | 0.3830 |
0.24 | 0.0948 | 0.56 | 0.2123 | 0.88 | 0.3106 | 1.20 | 0.3849 |
0.25 | 0.0987 | 0.57 | 0.2157 | 0.89 | 0.3133 | 1.21 | 0.3869 |
0.26 | 0.1026 | 0.58 | 0.2190 | 0.90 | 0.3159 | 1.22 | 0.3883 |
0.27 | 0.1064 | 0.59 | 0.2224 | 0.91 | 0.3186 | 1.23 | 0.3907 |
0.28 | 0.1103 | 0.60 | 0.2257 | 0.92 | 0.3212 | 1.24 | 0.3925 |
0.29 | 0.1141 | 0.61 | 0.2291 | 0.93 | 0.3238 | 1.25 | 0.3944 |
0.30 | 0.1179 | 0.62 | 0.2324 | 0.94 | 0.3264 | ||
0.31 | 0.1217 | 0.63 | 0.2357 | 0.95 | 0.3289 |
Продолжение приложения
x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
1.26 | 0.3962 | 1.59 | 0.4441 | 1.92 | 0.4726 | 2.50 | 0.4938 |
1.27 | 0.3980 | 1.60 | 0.4452 | 1.93 | 0.4732 | 2.52 | 0.4941 |
1.28 | 0.3997 | 1.61 | 0.4463 | 1.94 | 0.4738 | 2.54 | 0.4945 |
1.29 | 0.4015 | 1.62 | 0.4474 | 1.95 | 0.4744 | 2.56 | 0.4948 |
1.30 | 0.4032 | 1.63 | 0.4484 | 1.96 | 0.4750 | 2.58 | 0.4951 |
1.31 | 0.4049 | 1.64 | 0.4495 | 1.97 | 0.4756 | 2.60 | 0.4953 |
1.32 | 0.4066 | 1.65 | 0.4505 | 1.98 | 0.4761 | 2.62 | 0.4956 |
1.33 | 0.4082 | 1.66 | 0.4515 | 1.99 | 0.4767 | 2.64 | 0.4959 |
1.34 | 0.4099 | 1.67 | 0.4525 | 2.00 | 0.4772 | 2.66 | 0.4961 |
1.35 | 0.4115 | 1.68 | 0.4535 | 2.02 | 0.4783 | 2.68 | 0.4963 |
1.36 | 0.4131 | 1.69 | 0.4545 | 2.04 | 0.4793 | 2.70 | 0.4965 |
1.37 | 0.4147 | 1.70 | 0.4554 | 2.06 | 0.4803 | 2.72 | 0.4967 |
1.38 | 0.4162 | 1.71 | 0.4564 | 2.08 | 0.4812 | -2.74 | 0.4969 |
1.39 | 0.4177 | 1.72 | 0.4573 | 2.10 | 0.4821 | 2.76 | 0.4971 |
1.40 | 0.4192 | 1.73 | 0.4582 | 2.12 | 0.4830 | 2.78 | 0.4973 |
1.41 | 0.4207 | 1.74 | 0.4591 | 2.14 | 0.4838 | 2.80 | 0.4974 |
1.42 | 0.4222 | 1.75 | 0.4599 | 2.16 | 0.4846 | 2.82 | 0.4976 |
1.43 | 0.4236 | 1.76 | 0.4608 | 2.18 | 0.4854 | 2.84 | 0.4977 |
1.44 | 0.4251 | 1.77 | 0.4616 | 2.20 | 0.4861 | 2.86 | 0.4979 |
1.45 | 0.4265 | 1.78 | 0.4625 | 2.22 | 0.4868 | 2.88 | 0.4980 |
1.46 | 0.4279 | 1.79 | 0.4633 | 2.24 | 0.4875 | 2.90 | 0.4981 |
1.47 | 0.4292 | 1.80 | 0.4641 | 2.26 | 0.4881 | 2.92 | 0.4982 |
1.48 | 0.4306 | 1.81 | 0.4649 | 2.28 | 0.4887 | 2.94 | 0.4984 |
1.49 | 0.4319 | 1.82 | 0.4656 | 2.30 | 0.4893 | 2.96 | 0.4985 |
1.50 | 0.4332 | 1.83 | 0.4664 | 2.32 | 0.4898 | 2.98 | 0.4986 |
1.51 | 0.4345 | 1.84 | 0.4671 | 2.34 | 0.4904 | 3.00 | 0.49865 |
1.52 | 0.4357 | 1.85 | 0.4678 | 2.36 | 0.4909 | 3.20 | 0.49931 |
1.53 | 0.4370 | 1.86 | 0.4686 | 2.38 | 0.4913 | 3.40 | 0.49966 |
1.54 | 0.4382 | 1.87 | 0.4693 | 2.40 | 0.4918 | 3.60 | 0.49984 |
1.55 | 0.4394 | 1.88 | 0.4699 | 2.42 | 0.4922 | 3.80 | 0.49992 |
1.56 | 0.4406 | 1.89 | 0.4706 | 2.44 | 0.4927 | 4.00 | 0.49996 |
1.57 | 0.4418 | 1.90 | 0.4713 | 2.46 | 0.4931 | 4.50 | 0.49999 |
1.58 | 0.4429 | 1 1.91 | 0.4719 | 2.48 | 0.4934 | S 5.00 | 0.49999 |
Татьяна Владимировна Калашникова
исследование операций в экономике
Учебное пособие
Научный редактор
доктор техн. наук,
профессор
Редактор
Подписано к печати 27.11.2011. Формат 60х84/16. Бумага «Классика». Печать RISO. Усл. печ. л. 5,87. Уч.-изд. л. 5,32. Заказ. Тираж 80 экз. | ||
| Томский политехнический университет Система менеджмента качества Томского политехнического университета сертифицирована NATIONAL QUALITY ASSURANCE по стандарту ISO 9001:2000 |
|
|

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 |





