Исследование операций в экономике (стр. 6 )

Если игрок А придерживается своей максиминной стратегии  А2 , то игрок В должен выбрать свою минимаксную В3, с тем чтобы выигрыш игрока А (или что то же – проигрыш игрока В) был минимальным а23 = 0,4 (во 2-й строке матрицы (6.1)). На это игрок А должен ответить выбором опять же стратегии А2 , чтобы получить максимальный (в 3-м столбце) выигрыш: а23 = 0,4. Ответным ходом игрок В опять выбирает стратегию В3 и т. д.

Таким образом, если игроки А и В придерживаются своих максиминной и минимаксной стратегий, то ни один из них не может увеличить свой выигрыш, отступая от своей стратегии. Ситуация (А2 , В3) является в данной игре устойчивой.   

Нижняя и верхняя цены игры совпадают:

a = b = 0,4   

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решения игры. В таком случае можно получить оптимальное решение, случайным образом чередуя чистые стратегии.

Смешанной стратегией SA игрока А называется применение чистых стратегий А1, А2,…..Аi, …., Аm с вероятностями p1, p2,…., pi,….,pm, причем сумма вероятностей равна 1: . Цена игры будет удовлетворять неравенству .

Основная теорема теории игр – теорема Неймана. Каждая конечная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий.

В качестве примеров применения теории можно назвать решения по поводу проведения принципиальной ценовой политики, выхода на новые рынки, кооперации и создания совместных предприятий, определения лидеров и исполнителей в области инноваций, вертикальной интеграции и т. д. Положения данной теории в принципе можно использовать для всех видов решений, если на их принятие влияют другие действующие лица. Этими лицами, или игроками, необязательно должны быть рыночные конкуренты; в их роли могут выступать субпоставщики, ведущие клиенты, сотрудники организаций, а также коллеги по работе.

2.3. Геометрическая интерпретация игры 2´2

Пусть имеется два игрока А и В. У каждого из игроков по две стратегии (А1 и А2 у игрока А, В1 и В2 у игрока В). Игра с нулевой суммой.

По оси абсцисс отложим отрезок А1А2, то есть точка А1 изображает стратегию А1 (х=0), А2 – стратегию А2, все промежуточные точки – смешанные стратегии. На оси ординат откладываем выигрыш первого игрока, если второй применил стратегию В1. Аналогично строим второй график, если второй график выбрал стратегию В2.

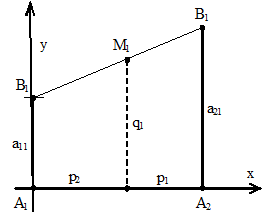
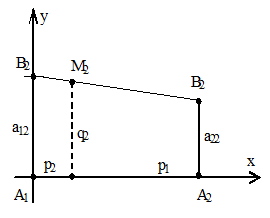
Рис. 2.1. Геометрическая интерпретация стратегий первого игрока

q1=a11p1+a21p2

q2=a12p1+a22p2 (ордината точки М1 и М2, соответственно)

В соответствии с принципом минимакса оптимальная стратегия SА* такова, что минимальный выигрыш игрока А (при наихудшем поведении игрока В) обращается в максимум.

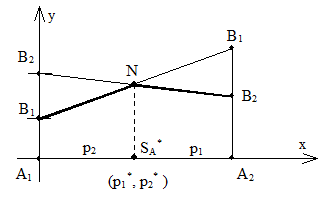
Рис. 2.2. Решение игры графическим способом

Отрезок В1N – минимальный выигрыш игрока А при использовании любой смешанной стратегии, если игрок В выбрал стратегию В1. Аналогично, отрезок В2N – выигрыш игрока А, если игрок В выбрал стратегию В2. Следовательно, оптимальную стратегию определяет точка N, то есть минимальный выигрыш достигает максимума.

Пример решения задачи.

Решить графически игру, заданную платежной матрицей:

Р=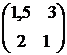

Определим верхнюю и нижнюю цены игры: 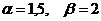. Следовательно, седловая точка отсутствует, будем искать решение в смешанных стратегиях. Отметим на графике величину выигрыша для каждой пары стратегий.

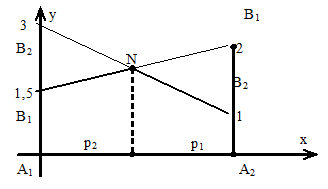
Рис. 2.3. Графическое решение игры

Запишем уравнение прямых, соответствующих величине выигрыша игрока А, если игрок В выбирает, соответственно, первую (B1) y= = 0,5 x + 1,5 и вторую (B2) y= –2x + 3 стратегии. Точка их пересечения N(0,6; 1,8). Следовательно, р2 = x = 0,6 – вероятность выбора игроком А второй стратегии; р1 = 1 – 0,6 = 0,4 – вероятность выбора игроком А первой стратегии. Цена игры = y = 1,8 – максимально возможный из минимально гарантированных выигрышей игрока А (либо минимально возможный из максимально гарантированных проигрышей игрока В).

Ø  Важно помнить. Графически можно решить игру, если в игре участвуют только два игрока и у одного из игроков имеется только две стратегии (у второго игрока – любое количество стратегий).

Задания для самостоятельной работы.

1. Для этой же задачи начертить график, записать уравнения прямых, найти вероятности и седловую точку для игрока В.

2. Применив методы теории игр, найти пропорцию использования посевной площади для производства трех сортов пшеницы, урожайность которых зависит от погодных условий. Критерий оптимальности – максимум валового урожая. Решить задачу графически.

Таблица 2.4

Размер урожайности каждого сорта в зависимости погодных условий

3. Игрок А записывает одно из двух чисел: 2 или 3. Игрок В записывает одно из трех чисел: 3, 4 или 5. Если числа одинаковой четности, то А выигрывает сумму чисел; и если четности чисел не совпадают, то сумму чисел выигрывает В. Построить платежную матрицу игры, определить верхнюю и нижнюю цену игры. Проверить наличие седловой точки.

Рассмотрим ситуацию, когда игра разрешается в чистых стратегиях, т. е. есть седловая точка. Графическое решение задачи может иметь следующие виды.

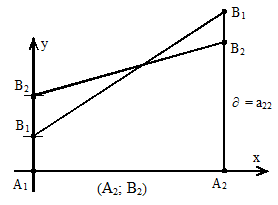
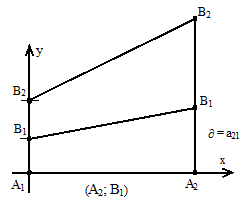
Рис. 2.4. Графики игр, разрешимых в чистых стратегиях

Пример решения задачи. Предприятие может выпускать 3 вида продукции А1, А2 и А3, получая при этом прибыль, зависящую от спроса, который может быть в одном из 4-х состояний (В1, В2, В3, В4). Элементы платежной матрицы характеризуют прибыль, которую получат при выпуске i-й продукции при j-м состоянии спроса. Определить оптимальные пропорции в выпускаемой продукции, гарантирующие максимизацию средней величины прибыли при любом состоянии спроса, считая его определенным. Задача сводится к игровой модели, в которой игра предприятия А против спроса В задана платежной матрицей.

Таблица 2.5

Платежная матрица игры

Прежде чем решить задачу, попытаемся упростить игру, проведя анализ платежной матрицы и отбросив заведомо невыгодные и дублирующие стратегии.

Для игрока В невыгодна вторая стратегия (столбец В2), так как все элементы этого столбца больше или равны элементам столбца В1, то есть при любой стратегии, выбранной игроком А, игрок В проигрывает больше в случае выбора второй стратегии вместо первой.

Поскольку a ¹ b, следовательно седловая точка отсутствует, решение будем искать в смешанных стратегиях.

Чтобы привести игру к задаче линейного программирования, обозначим:

.

Получим две взаимно двойственные задачи линейного программирования:

Для первого игрока:

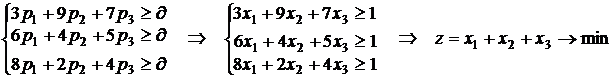(так как , то .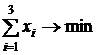

Поскольку .

И для второго игрока:

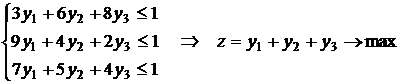
Вторую задачу на максимум решать легче. Решаем ее симплексным методом. Получаем следующий результат:

.

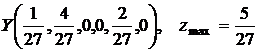Последняя запись целевой функции имеет вид:

.

Следовательно, можем записать решение взаимно двойственной задачи, то есть задачи для первого игрока, используя теорию двойственности. Это решение будет иметь вид:

Цена игры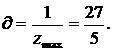

Найдем вероятности выбора стратегий:

,

То есть .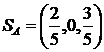

Данный результат означает, что предприятие должно выпустить 40 % продукции А1 и 60 % продукции А3, а продукцию А2 выпускать не надо. Тогда максимально гарантированное из минимально возможных значений средней величины прибыли составит 5,4 ден. ед., независимо от спроса покупателей.

Задание для самостоятельной работы.

По данному решению записать вероятности выбора стратегий игроком В, какой экономический смысл имеет найденное решение.

При решении произвольной конечной игры размера m×n рекомендуется придерживаться следующей схемы:

1)  Исключить из платежной матрицы заведомо невыгодные стратегии по сравнению с другими стратегиями. Такими стратегиями для игрока А (игрока В) являются те, которым соответствуют строки (столбцы) с элементами заведомо меньшими (большими) по сравнению с элементами других строк (столбцов).

2)  Определить верхнюю и нижнюю цены игры и проверить, имеет ли игра седловую точку. Если седловая точка есть, то соответствующие ей стратегии игроков будут оптимальными, а цена совпадает с верхней (нижней) ценой.

3)  Если седловая точка отсутствует, то решение следует искать в смешанных стратегиях. Для игр размера m×n рекомендуется симплексный метод, для игр размера 2×2, 2×n, n×2 возможно геометрическое решение.

На практике реализация решения в смешанных стратегиях может происходить несколькими путями. Первый состоит в физическом смешении чистых стратегий в пропорциях, заданных вероятностями pi. Другой путь – при многократном повторении игры предполагает применение в каждой партии чистых стратегий в виде случайной последовательности, причем каждая из них – с частотой, равной ее вероятности в оптимальном решении.

Однако существуют определенные границы применения аналитического инструментария теории игр. В следующих случаях он может быть использован лишь при условии получения дополнительной информации.

Во-первых, это тот случай, когда у предприятий сложились разные представления об игре, в которой они участвуют, или когда они недостаточно информированы о возможностях друг друга. Например, может иметь место неясная информация о платежах конкурента (структуре издержек). Если неполнотой характеризуется не слишком сложная информация, то можно оперировать сопоставлением подобных случаев с учетом определенных различий.

Во-вторых, теорию игр трудно применять при множестве ситуаций равновесия. Эта проблема может возникнуть даже в ходе простых игр с одновременным выбором стратегических решений.

В-третьих, если ситуация принятия стратегических решений очень сложна, то игроки часто не могут выбрать лучшие для себя варианты. Например, на рынок в разные сроки могут вступить несколько предприятий или реакция уже действующих там предприятий может оказаться более сложной, нежели быть агрессивной или дружественной.

Экспериментально доказано, что при расширении игры до десяти и более этапов игроки уже не в состоянии пользоваться соответствующими алгоритмами и продолжать игру с равновесными стратегиями.

Ø  Важно помнить. Теория игр является очень сложной областью знания. При обращении к ней надо соблюдать известную осторожность и четко знать границы применения. Слишком простые толкования, принимаемые фирмой самостоятельно или с помощью консультантов, таят в себе скрытую опасность. Анализ и консультации на основе теории игр из-за их сложности рекомендуются лишь для особо важных проблемных областей. Опыт фирм показывает, что использование соответствующего инструментария предпочтительно при принятии однократных, принципиально важных плановых стратегических решений, в том числе при подготовке крупных кооперационных договоров.

Пример решения задачи.

Швейная фабрика выпускает брюки и шорты, сбыт которых зависит от состояния погоды. Затраты фабрики на единицу продукции составили: брюки – 15 ден. ед., шорты – 10 ден. ед. Цена реализации: брюки – 21 ден. ед., шорты – 14 ден. ед. Фабрика может реализовать при теплой погоде 120 брюк и 300 шорт, а при прохладной погоде: 370 брюк и 100 шорт.

Составим платежную матрицу игры.

Таблица 2.6

Матрица выигрыша фабрики

Погода

Вычислим значения элементов матрицы:

= 120*(21 – 15) + 300*(14 – 10) = 1920 – прибыль фабрики, если продукция выпущена по плану теплой погоды и погода оказалась теплой;

= 370*(21 – 15) + 100*(14 – 10) = 2620 – прибыль фабрики, если продукция выпущена по плану холодной погоды и погода оказалась холодной;

= 120*(21 – 15) + 100*(14 – 10) – 200*10 = –880 – прибыль фабрики, если продукция выпущена по плану теплой погоды, а погода оказалась холодной;

= 120*(21 – 15) + 100*(14 – 10) – 250*15 = –2630 – прибыль фабрики, если продукция выпущена по плану холодной погоды, а погода оказалась теплой.

Таким образом, платежная матрица данной игры имеет вид:

Таблица 2.7

Платежная матрица игры

Погода

Обозначим: р1 – вероятность выбора фабрикой первой стратегии (то есть производства продукции по плану теплой погоды), р2 – вероятность выбора фабрикой второй стратегии (то есть производства продукции по плану холодной погоды). Тогда:

(1920* р1 – 2630* р2) – прибыль фабрики, если погода будет теплой;

(–880* р1 + 2620* р2) – прибыль фабрики, если погода будет холодной.

Чтобы прибыль фабрики не зависела от погоды, надо найти такие р1 и р2, что (1920* р1 – 2630* р2) = (–880* р1 + 2620* р2). Учитывая свойство вероятностей: р1 + р2 = 1, решаем уравнение.

1920* р1 – 2630*(1 – р1) = –880* р1 + 2620* (1 – р1)

Раскрывая скобки и приводя подобные, получаем:

р1*(1920 + 2630 + 880 + 2620) = (2620 + 2630)

. Тогда р2 = 1–0,652 = 0,348.

Тогда план выпуска продукции для фабрики должен составить:

количество брюк = 120*0,652 + 370*0,348 = 207 шт.;

количество шорт = 300*0,652 + 100*0,348 = 230 шт.

При таком плане производства фабрика гарантирует себе прибыль в размере 1920*0,652 – 2630*0,348 = 337 ден. ед.

Задание для самостоятельной работы.

Применив методы теории игр, решить следующие экономические задачи.

1. Предприятие выпускает скоропортящуюся продукцию, которую можно сразу отправить к потребителю (А1), отправить на склад для хранения (А2) или подвергнуть дополнительной обработке для длительного хранения (А3). Потребитель может приобрести продукцию немедленно (В1), в течение небольшого времени (В2) или после длительного периода времени (В3).

В случае стратегии А2 и А3 предприятие несет дополнительные затраты на хранение и обработку продукции, которая не требуется для А1, однако при А2 следует учесть возможные убытки из-за порчи продукции, если потребители выберут стратегии В2 и В3. Определить оптимальные пропорции выпуска продукции, руководствуясь минимаксным критерием, при следующей матрице затрат.

Таблица 2.8

Платежная матрица игры

2. Швейная фабрика выпускает платья и костюмы, сбыт которых зависит от состояния погоды. Затраты фабрики на единицу продукции составили: платья – 8 ден. ед., костюмы – 27 ден. ед. Цена реализации: платья – 17 ден. ед., костюмы – 48 ден. ед. Фабрика может реализовать при теплой погоде 1975 платьев и 600 костюмов, а при прохладной погоде: 625 платьев и 1000 костюмов.

Максимизировать среднюю величину дохода от реализации продукции, учитывая капризы природы, т. е. составить такой план выпуска продукции, при котором гарантированная минимально возможная величина средней прибыли была бы максимальной, независимо от погоды.

Что означают следующие термины и понятия?

Теперь вы должны уметь:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9