o составлять экономико-математические модели задач, применяя методы теории игр;
o решать матричные игры графическим методом;
o приводить задачи теории игр к задачам линейного программирования;
o определять, разрешима ли игра в чистых стратегиях;
o определять оптимальные смешанные стратегии для игроков, то есть находить вероятности применения чистых стратегий;
o классифицировать игру;
o анализировать результаты решения игры;
o решать игру аналитическим способом, если в игре участвуют только два игрока и у одного из них имеется только две стратегии.
Контрольные вопросы:
1. Понятие игры.
2. Какие проблемы решает теория игр (теория конфликтных ситуаций)?
3. Классификация игр.
4. Что значит решить игру?
5. Что такое платежная матрица?
6. Что называется чистой ценой игры?
7. Когда в игре существует седловая точка?
8. Геометрическая интерпретация игры.
9. Схема решения игры.
10. Понятие смешанных стратегий, когда они необходимы, как применить их на практике.
11. Какие типы экономических задач сводятся к игровой модели?
3. СЕТЕВОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ
Теория графов тесно связана со многими направлениями математического моделирования. Особенно важная взаимосвязь существует между теорией графов и исследованием операций, теорией игр, сетевым планированием и управлением.
Граф – это конструкция из вершин и ребер. Вершины – это точки, а ребра – соединяющие их линии. Ребра могут быть ориентированными дугами. Граф называется Эйлеровым, если существует путь, позволяющий прийти в ту же вершину, из которой вышли, пройдя по каждому ребру, только один раз. Граф называется Гамильтоновым, если существует путь, позволяющий обойти все вершины, заходя в каждую только один раз. Деревом называется граф, любые две вершины которого соединены только одним ребром.
С помощью теории графов в детстве многие из вас решали задачу: нарисовать домик, не отрывая ручки от бумаги, то есть рисовали Эйлеровый граф. Гамильтонов граф применяется курьерами, которым необходимо обойти несколько организаций, естественно, заходя в каждую один раз, и они стремятся минимизировать свой общий путь – так называемая задача коммивояжера.
Пример решения задачи.
Сетевая задача, которая решается как транспортная.
Компания имеет восемь крупных оптовых складов. Отдел сбыта принял решение значительно снизить цену одного дорогостоящего изделия с целью ликвидации образовавшегося запаса этих изделий. Руководство намерено разместить имеющиеся в наличии запасы на указанных восьми складах в соответствии с прогнозами сбыта в этих районах. Таким образом, надо перераспределить некоторую часть запасов. Числа у складов – это избыток или недостаток товара. Склады 2, 4, 5, 6, 7 – промежуточные. Все другие склады – источники, если избыток товаров и стоки – если требуется дополнительный запас. Сij – затраты на перевозку одного изделия со склада i на склад j.
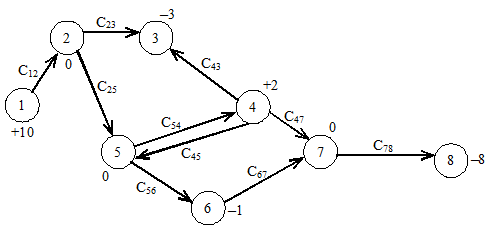
Рис. 3.1. Схема перевозок товаров между складами
Задание для самостоятельной работы. Составить экономико-математическую модель транспортной задачи.
3.1. Сетевая модель и ее основные элементы
Аппарат сетевого планирования и управления – это совокупность моделей и методов планирования и управления выполнением комплекса работ, в основе которых лежит понятие сетевого графика или сетевой модели. Под комплексом работ понимается любая задача или проблема, для решения которой необходимо выполнить достаточно большое количество разнообразных работ.
Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в форме сети, изображение которой называется сетевым графиком.
Модели и методы СПУ предназначены для решения двух основных проблем:
· формирование календарного плана реализации комплекса работ;
· принятие эффективных решений в процессе выполнения этого плана.
Главными элементами сетевой модели являются события и работы. События обозначаются вершинами графа, а работы ориентированными дугами.
Событие – это момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. Предполагается, что событие не имеет продолжительности и свершается как бы мгновенно. Среди событий сетевой модели выделяют исходное (начальное) – не имеет предшествующих работ и событий, завершающее (конечное) – не имеет последующих работ и событий.
Работа может быть трех видов: действительная работа – протяженный во времени процесс, требующий затрат ресурсов; ожидание – протяженный во времени процесс, не требующий затрат труда; фиктивная работа (зависимость) – логическая связь между двумя или несколькими работами, не требующими затрат труда, материальных ресурсов и времени.
Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Полный путь (L) – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим. Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, расположенные на этом пути. Длина критического пути называется критическим временем (сроком) сетевого графика (Ткр). Критическое время – это наименьшее время выполнения всего комплекса работ. Сетевой график может иметь несколько различных критических путей, но все они имеют одну и ту же длину.
3.2. Правила построения сетевых графиков
При построении сетевого графика необходимо соблюдать ряд правил.
1. В сетевой модели не должно быть «тупиковых» событий, то есть событий, из которых не выходит ни одна работа, за исключением завершающего события.
2. В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
3. В сети не должно быть замкнутых контуров и петель, то есть путей, соединяющих некоторые события с ними же самими.
4. Любые два события должны быть непосредственно связаны не более чем одной работой.
5. В сети рекомендуется иметь одно исходное и одно завершающее событие.
6. Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.
Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1 и обводится кружком. Из начального события выпускают стрелки, соответствующие работам, которым не предшествуют какие-либо другие работы. По определению, момент завершения работы является событием. Поэтому каждая стрелка завершается кружком – событием, в котором проставляется номер этого события. Нумерация событий произвольная. На следующем этапе построения изображаем работы, которым предшествуют уже нарисованные работы (то есть которые опираются на уже построенные работы) и т. д. На следующем этапе отражаем логические взаимосвязи между работами и определяем конечное событие сетевого графика, на которое не опираются никакие работы. Построение закончено, далее необходимо провести упорядочение сетевого графика.
Простой метод упорядочения сетевого графика основан на понятии ранга события:
- все события сетевого графика подразделяются на ранги,
- к одному рангу может относиться несколько событий,
- нумерация событий производится в соответствии с принадлежностью к тому или иному рангу,
- чем выше ранг, тем больший номер имеет событие,
- внутри одного ранга нумерация событий произвольная.
Начальное событие относим к нулевому рангу и перечеркиваем одной чертой все работы, выходящие из этого события. К первому рангу относим те события, которые не имеют входящих неперечеркнутых стрелок. Далее перечеркиваем двумя чертами работы, выходящие из событий первого ранга. Ко второму рангу относим те события, которые не имеют входящих неперечеркнутых стрелок и т. д.
3.3. Временные параметры сетевых графиков
Параметры событий:
• ранний (ожидаемый) срок tp(i) свершения i-го события определяется продолжительностью максимального пути, предшествующего этому событию: 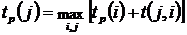 ;
;
• поздний (предельный) срок tп(i) свершения i-го события равен: 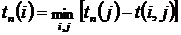 ;
;
• резерв времени R(i) i-го события определяется как разность между поздним и ранним сроками его свершения: ![]() .
.
Резерв времени показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ. Ранний срок наступления завершающего события сети равен длине критического пути. Критические события резервов времени не имеют. События с нулевыми резервами времени определяют топологию критического пути.
Параметры работ:
• ранний срок tрн(i,j) начала работы (i,j) совпадает с ранним сроком наступления начального (предшествующего) события i :
![]() ;
;
• ранний срок tро(i,j) окончания работы (i,j) определяется по формуле:
![]() ;
;
• поздний срок tпо(i,j) окончания работы (i,j) совпадает с поздним сроком конечного события:
![]() ;
;
• поздний срок tпн(i,j) начала работы (i,j) определяется по формуле:
![]() .
.
Резерв времени пути R(L) определяется как разность между длиной критического и рассматриваемого пути: R(L)=tкр – t(L).
Полный резерв времени Rп (i,j) работы (i,j) показывает, на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится:
Rп(i, j) = tп(j) – tp(i) – t(i, j).
Ø Важно помнить. Работы, лежащие на критическом пути, резервов не имеют.
Пример решения задачи. Для заданного сетевого графика рассчитать все параметры событий и работ, определить критический путь и его длину.
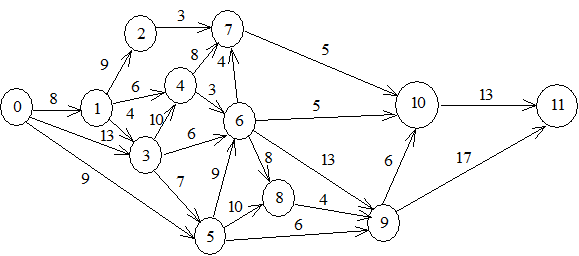
Рис. 3.2. Сетевой график
Расчет временных параметров событий удобно представить в таблице.
Таблица 3.1
Параметры событий сетевого графика
Номер события | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Ранний срок tр(i) | 0 | 8 | 17 | 13 | 23 | 20 | 29 | 33 | 37 | 42 | 48 | 61 |
Поздний срок tп(i) | 0 | 9 | 40 | 13 | 26 | 20 | 29 | 43 | 38 | 42 | 48 | 61 |
Резерв времени R(i) | 0 | 1 | 23 | 0 | 3 | 0 | 0 | 10 | 1 | 0 | 0 | 0 |
Критический путь образуют следующие события:
![]() . Топологию критического пути определяют события, резерв времени которых равен нулю. Его продолжительность составляет 61 день (ранний срок свершения последнего события).
. Топологию критического пути определяют события, резерв времени которых равен нулю. Его продолжительность составляет 61 день (ранний срок свершения последнего события).
Для определения временных параметров работ также используем таблицу, в которую сведем результаты вычислений. Расчеты проводим с помощью приведенных выше формул.
Таблица 3.2
Параметры работ сетевого графика
№ | Работа (i, j) | Продолжитель-ность работы (i, j) | Сроки начала и окончания работы | Резерв времени Rп(i,j) | |||
tрн(i, j) | tро(i, j) | tпн(i, j) | tпо(i, j) | ||||
1 | (0, 1) | 8 | 0 | 8 | 1 | 9 | 1 |
2 | (0, 3) | 13 | 0 | 13 | 0 | 13 | 0 |
3 | (0, 5) | 9 | 0 | 9 | 11 | 20 | 11 |
4 | (1, 2) | 9 | 8 | 17 | 31 | 40 | 23 |
5 | (1, 4) | 6 | 8 | 14 | 20 | 26 | 12 |
6 | (1, 3) | 4 | 8 | 12 | 9 | 13 | 1 |
7 | (2, 7) | 3 | 17 | 20 | 40 | 43 | 23 |
8 | (3, 4) | 10 | 13 | 23 | 16 | 26 | 3 |
9 | (3, 5) | 7 | 13 | 20 | 13 | 20 | 0 |
10 | (3, 6) | 6 | 13 | 19 | 23 | 29 | 10 |
11 | (4, 7) | 8 | 23 | 31 | 35 | 43 | 12 |
12 | (4, 6) | 3 | 23 | 26 | 26 | 29 | 3 |
13 | (5, 6) | 9 | 20 | 29 | 20 | 29 | 0 |
14 | (5, 8) | 10 | 20 | 30 | 28 | 38 | 8 |
15 | (5, 9) | 6 | 20 | 26 | 36 | 42 | 16 |
16 | (6, 7) | 4 | 29 | 33 | 39 | 43 | 10 |
Продолжение таблицы 3.2 | |||||||
17 | (6, 10) | 5 | 29 | 34 | 43 | 48 | 14 |
18 | (6, 9) | 13 | 29 | 42 | 29 | 42 | 0 |
19 | (6, 8) | 8 | 29 | 37 | 30 | 38 | 1 |
20 | (7, 10) | 5 | 33 | 38 | 43 | 48 | 10 |
21 | (8, 9) | 4 | 37 | 41 | 38 | 42 | 1 |
22 | (9, 10) | 6 | 42 | 48 | 42 | 48 | 0 |
23 | (9, 11) | 17 | 42 | 59 | 44 | 61 | 2 |
24 | (10, 11) | 13 | 48 | 61 | 48 | 61 | 0 |
3.4. Сетевое планирование в условиях неопределенности

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 |




