В этом случае уравнение тиристорного преобразователя будет иметь вид:
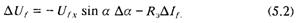
Для систем тиристорного самовозбуждения с последовательными трансформаторами (рис. 5.1,6) коммутирующей эдс является геометрическая сумма векторов напряжения и тока синхронного генератора
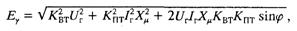
где Квт, Kпт — коэффициенты трансформации выпрямительного и последовательного трансформаторов соответственно; Хμ — реактивность намагничивания последовательного трансформатора, отнесенная к базисному сопротивлению генератора.
Среднее значение напряжения тиристорного преобразователя системы самовозбуждения, работающего на холостом ходу при нулевом угле управления в режиме горения вентилей 2—3, определяется выражением
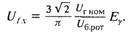
Эквивалентное сопротивление тиристорного преобразователя зависит от реактивности рассеяния выпрямительного Хвт и последовательного Xпт трансформаторов, а также от реактивности намагничивания последовательного трансформатора:
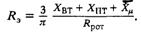
Следует иметь в виду, что величины реактивных сопротивлений, входящих в последнюю формулу, приведены ко вторичной обмотке трансформаторов и выражены в омах.
Линеаризованная система уравнений системы тиристорного самовозбуждения имеет вид:
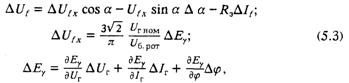
где
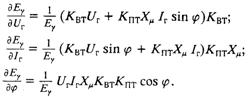
Таким образом, линейная математическая модель статической тиристорной системы независимого возбуждения представляет собой уравнение (5.2), а системы самовозбуждения — систему уравнений (5.3).
5.2. Математическая модель
системы управления тиристорами
Современные системы управления тиристорами, построенные по вертикальному принципу, имеют арккосинусную зависимость угла сдвига отпирающего импульса относительно первой гармоники питающего напряжения. Работа такой системы описывается следующим уравнением:
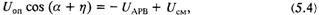
где Uоп — амплитуда опорной синусоиды; η — угол сдвига между опорной синусоидой и первой гармоникой напряжения питания тиристорного преобразователя; Uсм — напряжение смещения системы управления тиристорами.
7*
Напряжением питания тиристорного преобразователя независимой системы возбуждения является напряжение вспомогательного генератора; для тиристорного преобразователя системы самовозбуждения напряжением питания будет геометрическая сумма векторов напряжения и тока главного генератора. Если не учитывать переходных процессов в обмотках вспомогательного генератора или выпрямительного и группы последовательных трансформаторов, то можно принять величину питающего напряжения равной величине коммутирующей эдс. В этом случае для независимой системы и для системы самовозбуждения будет справедливо соотношение
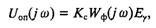
где Кс — коэффициент трансформации трансформатора синхронизации; Wф(jω) — частотная характеристика фильтра, который выделяет из питающего напряжения преобразователя его первую гармоническую составляющую.
Величины амплитуды и фазы опорной синусоиды, входящие в уравнение (5.4), определяются из уравнений:
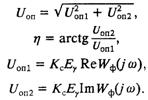
Линеаризация дает систему уравнений, описывающую работу системы управления тиристорами для режима малых отклонений:
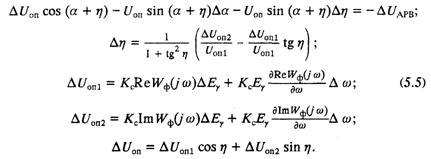
Таким образом, последняя система уравнений совместно с уравнением (5.2) или системой уравнений (5.3) является математической моделью статической системы возбуждения, связывающей величину изменения напряжения возбуждения ΔUf с изменением выходного напряжения регулятора ΔUАРВ.
При работе синхронного генератора параллельно с сетью большой мощности частота напряжения питания тиристорного преобразовате-
ля меняется незначительно, поэтому можно положить Δω = 0. Тогда система уравнений (5.5) сведется к двум уравнениям:
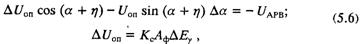
где
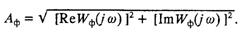
Однако при исследовании устойчивости регулирования и при расчетах переходных процессов автономных систем необходимо использовать полную систему уравнений (5.5).
5.3. Упрощенная математическая модель
статической тиристорной системы возбуждения
Упрощенное уравнение тиристорного преобразователя получается при пренебрежении величиной реактивности коммутации. В этом случае
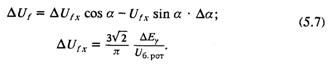
Если пренебречь инерционностью фильтра системы управления тиристорами и положить, что при синхронной частоте Аф = 1 и η = 0, уравнения СУ Т упрощаются:
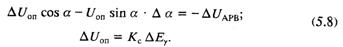
Совместное решение систем уравнений (5.7) и (5.8) с учетом уравнений установившегося режима дает

Отсюда следует, что приращение напряжения возбуждения линейно связано с приращением выходного напряжения регулятора, причем коэффициент передачи равен отношению кратности форсирования возбуждения к амплитуде опорной синусоиды. Этот вывод справедлив для независимой системы возбуждения и системы самовозбуждения.
5.4. Бесщеточная система возбуждения
В работах [62—64 ] была предложена математическая модель бесщеточного возбудителя (рис. 5.2), замещающая диодный выпрямитель моста внешней характеристикой. При этом предполагалось, что угол коммутации не изменяется в течение переходного процесса. В действительности же угол коммутации, оставаясь постоянным во всех установившихся режимах диодного преобразователя, в переходных режимах существенно меняется. Расчеты и эксперименты показывают, что в диапазоне от 0.2 до 2 Гц амплитуда частотной характеристики угла коммутации изменяется на 25 дБ, а фаза — на 150°. Поэтому учет изменения угла коммутации в переходном процессе обязателен. Кроме того, при составлении математического описания возбудителя влияние поперечного демпферного контура не учитывалось, а влияние продольного демпферного контура без достаточных на то оснований учитывалось упрощенно. Принятые допущения не позволяют использовать предложенные ранее модели для исследования устойчивости систем автоматического регулирования возбуждения. Поэтому была разработана новая модель [50], в которой мостовой диодный преобразователь моделируется по основной гармонике тока питающей сети и по его внешним характеристикам. При этом предполагается, что в течение коммутационного цикла по-токосцепления обмоток обращенного синхронного генератора, а также ток и напряжение главного генератора постоянны. Эти допущения позволяют рассматривать возбудитель как мостовой преобразователь, в котором коммутирующей эдс является сверхпереходная эдс Е'' обращенного синхронного генератора, приложенная за реактивностью коммутации Хγ = 1/2 (Х''qв + Х''dв). Для составления полной математической модели запишем систему уравнений обращенного синхронного генератора с учетом продольного и поперечного де-
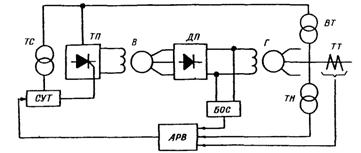
Рис. 5.2. Бесщеточная диодная система возбуждения.
Обозначения: ТС — трансформатор синхронизации; СУТ — система управления тиристорами; ТП — тиристорный преобразователь; В — возбудитель; ДП — диодный преобразователь; АРВ — автоматический регулятор возбуждения; Б0С — блок обратной связи; Г — генератор; ВТ — выпрямительный трансформатор; ТН — трансформатор напряжения; ТТ — трансформатор тока.
мпферных контуров в системе относительных единиц [16]:
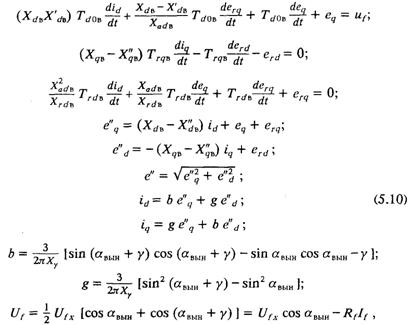
где
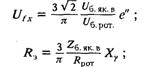
Uб. як. в — базисное значение напряжения якоря возбудителя, определяемое как номинальное линейное напряжение обращенного синхронного генератора; Zб. як. в. — базисное сопротивление якоря обращенного синхронного генератора.
Постоянные времени и реактивные сопротивления рассчитываются в соответствии с общепринятой схемой замещения [16 ] по следующим соотношениям:
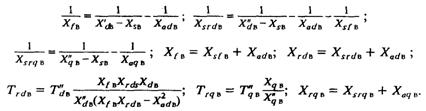
Величина эквивалентного сопротивления диодного преобразователя характеризует режим работы вентилей. Если RЭ ≤ 1/3, то преобразователь работает в режиме 2—3 и αвын = 0. При RЭ > 1/3 вентили диодного моста работают в режиме 3—3 и γ = 60°.
Для режима 2—3 величина угла коммутации и коэффициенты, входящие в систему уравнений (5.10), рассчитываются по формулам:
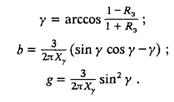
При работе вентилей преобразователя в режиме 3—3 значения вынужденного угла зажигания и коэффициентов определяются по уравнениям:
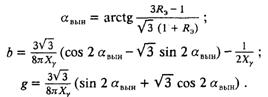
Для использования модели диодной бесщеточной системы возбуждения при расчетах статической устойчивости параллельной работы синхронных генераторов требуется ее линеаризация. Линейная математическая модель в приращениях переменных имеет вид:
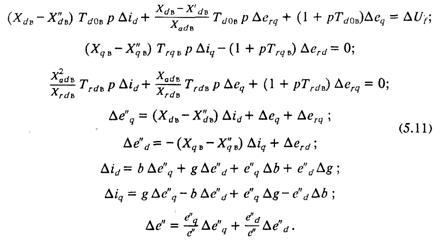
При работе вентилей диодного преобразователя в режиме 2—3 последняя система уравнений должна быть дополнена:
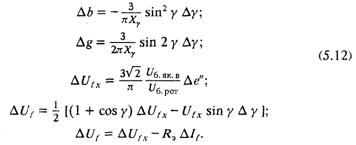
При работе вентилей диодного моста в режиме 3—3 уравнения приращения переменных, определяющих проводимость преобразователя, запишутся в виде:
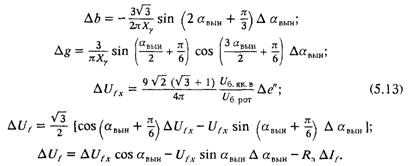
Таким образом, система (5.11), дополненная в зависимости от режима работы вентилей уравнениями (5.12) или (5.13), является подробной математической моделью вращающегося диодного возбудителя.
5.5. Упрощенная математическая модель
бесщеточного диодного возбудителя
Менее громоздкая, но достаточно точная модель для анализа поведения синхронного генератора и расчетов устойчивости его параллельной работы с энергосистемой может быть получена при пренебрежении влиянием демпферных контуров и изменением поперечного тока якоря возбудителя. Для этого в системе уравнений (5.11) следует положить равными нулю Δerq, Δerd, Δiq. Тогда, исключив промежуточные переменные, получаем достаточно простое уравнение, описывающее работу возбудителя [50 ]:
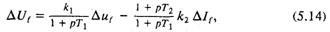
 |
где
Формулы для выражений, входящих в (5.15), в зависимости от режима работы диодного преобразователя приведены в табл. 5.1.
Более точное определение величин ki и Тi может быть выполнено на базе экспериментальных или расчетных (по полным уравнениям возбудителя) частотных характеристик.
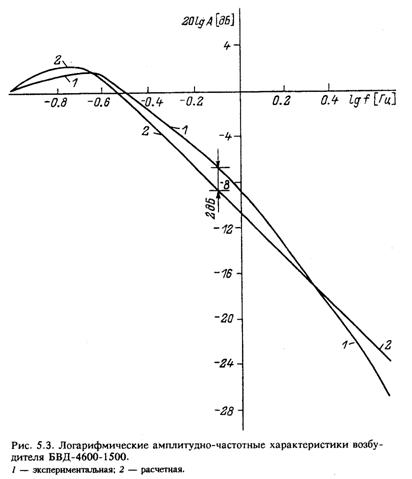
Для этой цели был проведен расчет частотных характеристик возбудителя типа БВД по полным уравнениям математической модели (5.11) для режимов холостого хода и короткого замыкания. Из анализа расчетных характеристик были определены значения коэффициентов и постоянных времени, входящих в уравнение (5.14). Сравнение полученных значений параметров со значениями, определенными по формулам (5.15), показало их отличие в пределах 5—7 % (табл. 5.2).
С целью определения зависимости постоянных времени и коэффициентов, входящих в уравнение (5.14), от режима работы возбудителя были выполнены расчеты величин этих параметров для ряда значений выходной координаты (напряжение возбуждения генератора). В результате этого установлено, что параметры математической модели возбудителя, представленной в такой форме, практически не зависят от режима работы синхронного генератора. Поэтому будет справедливо представить модель бесщеточного возбудителя в форме:
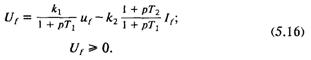
Модель возбудителя была получена при большом количестве допущений, указанных выше. Поэтому для определения степени соответствия разработанной математической модели оригиналу потребовалась экспериментальная проверка. Такая проверка была выполнена в период пусконаладочных испытаний турбогенератора ТВВ-1000-4 с возбудителем БВД. Для этого в режиме короткого замыкания энергоблока определены частотные характеристики системы возбуждения. Входной синусоидальный сигнал подавался на вход системы управления тиристорами; выходной сигнал снимался с делителя обратной связи, т. е. был пропорционален напряжению ротора. Полученные частотные характеристики приведены на рис. 5.3,

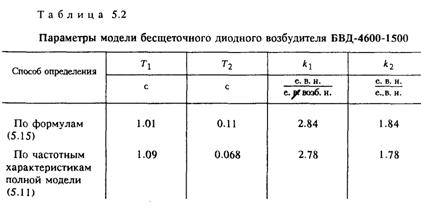
5.4 (кривые 1). Расчет параметров, входящих в уравнение (5.16), выполненный по предложенной методике для возбудителя БВД, дал результаты, приведенные в табл. 5.2.
Уравнение, связывающее входной сигнал с напряжением возбуждения возбудителя, определяется упрощенной моделью тиристорного преобразова:

Уравнение обмотки возбуждения в режиме короткого замыкания энергоблока имеет вид

где
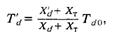
ХT — сопротивление рассеяния блочного трансформатора. Совместное решение (5.16)—(5.18) дает
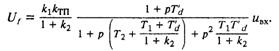
Из последнего уравнения были определены расчетные частотные характеристики, представленные на рис. 5.3 и 5.4 (кривые 2). Сравнение расчетных кривых с экспериментальными показывает, что в диапазоне от 0.5 до 4 Гц амплитудные характеристики отличаются друг от друга не более чем на 2 дБ, а фазовые — не более чем на 2.5°.
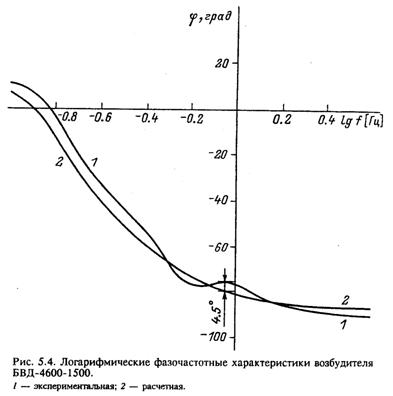
Таким образом, расчеты и эксперименты подтвердили, что, несмотря на свою кажущуюся простоту, упрощенная модель диодного бесщеточного возбудиявляется достаточно точной.
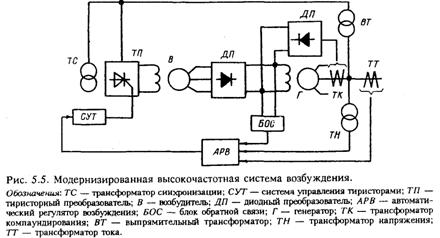
5.6. Модернизированная высокочастотная система возбуждения
С 70-х годов турбогенераторы мощностью от 100 до 500 МВт оснащались высокочастотной системой возбуждения. За истекшие годы произошло моральное и физическое старение аппаратуры регулирования этих систем, выполненных на магнитных усилителях. В настоящее время эти системы не удовлетворяют требованиям по части быстродействия, ограничения перегрузок и минимального возбуждения, а также по части резервирования основного АРВ. В связи с этим встал вопрос об их модернизации. Модернизация высокочастотной системы возбуждения заключается в замене аппаратуры, выполненной на магнитных усилителях, полупроводниковым регулятором АРВ-СДП1 и тиристорным преобразователем, в отказе от подвозбудителя и исключении из схемы системы возбуждения последовательной обмотки возбуждения возбудителя [61 ]. Схема модернизированной высокочастотной системы возбуждения приведена на рис. 5.5. Ток ротора синхронного генератора складывается из токов двух диодных мостов, питаемых от вращающегося возбудителя (If1) и от трансформаторов силового компаундирования (If2). В связи с этим очевидно следующее уравнение:

Уравнение, описывающее работу диодного выпрямительного моста, питающегося напряжением вращающегося возбудителя и работающего на обмотку возбуждения синхронного генератора, было получено ранее (5.14) при рассмотрении бесщеточной системы возбуждения:
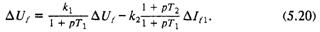
Коэффициенты и постоянные времени, входящие в последнее уравнение, определяются по формулам (5.15). При этом в качестве реактивности коммутации следует брать реактивность рассеяния возбудителя Хγ = Хsв. Режим работы преобразователя, питаемого напряжением возбудителя, зависит от распределения тока между мостами и определяется эквивалентным сопротивлением диодного преобразователя:
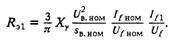
Если RЭ ≤ 1/3, то преобразователь работает в режиме 2—3, если
RЭ > l/З, то—в режиме 3—3.
Работа диодного выпрямителя силового компаундирования может быть описана уравнением внешней характеристики. При этом коммутирующей эдс является величина, пропорциональная произведе-
нию тока статора на реактивность шунта намагничивания, а реактивностью коммутации — сумма реактивных сопротивлений намагничивания и рассеяния трансформатора компаундирования. Следовательно, для режима малых отклонений справедливо следующее уравнение:
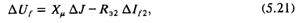
где для случая соединения трансформаторов компаундирования по схеме треугольника
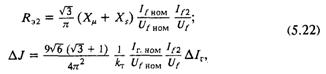
где Хμ , Хs — реактивные сопротивления намагничивания и рассеяния трансформаторов компаундирования, приведенные ко вторичной обмотке и выраженные в омах; kт — коэффициент трансформации трансформаторов компаундирования.
Решив совместно уравнения (5.19)—(5.22), получим:
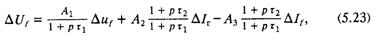
где
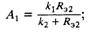
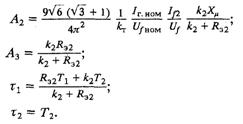
Для вычисления коэффициентов линеаризованных уравнений требуется определить распределение токов между диодными выпрямительными мостами. Ток диодного моста, питаемого от трансформатора силового компаундирования, определяется как корень квадратного уравнения
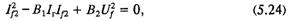
где
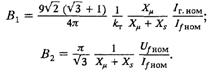
Очевидно, что ток выпрямительного моста, питаемого от высокочастотного генератора, определяется как разность токов

В качестве примера выполним расчет параметров математической модели высокочастотного возбудителя турбогенератора ТВФ-120-2 для номинального режима работы. Номинальные величины турбогенератора имеют значения: Uf ном = 300 В; If ном = 1830 А; Iг. ном =7763 А.
Параметры трансформаторов силового компаундирования имеют следующие значения: Хμ = 3 Ом, Xs = 0.0275 Ом, kт = 14.
Величины параметров высокочастотного возбудителя равны:
Sв. ном = 340 кВ*А, Uв. ном = 280 В, Xd в =1.24, X'd в = 0.64, Xγ = 0.57,
Td 0в= 0.64 с.
В номинальном режиме работы турбогенератора Uf= 1.0, If = 1.0,
Iг = 1.0.
Коэффициенты квадратного уравнения (5.24) равны В1Iг = 0.831, B2U2f = 0.098.
Ток выпрямителя, питающегося от трансформаторов силового компаундирования, определенный как корень уравнения (5.24), равен If2 =0.689.
Ток выпрямителя, питающегося от высокочастотного возбудителя, вычисляется по формуле (5.25), If1 = 0.311.
Уместно заметить, что в период пусконаладочных работ на высо - кочастотной системе турбогенератора ТВФ-120-2 был произведен замер распределения токов между диодными мостами в номинальном режиме работы турбогенератора. Измерения дали следующие результаты: If1 = 580 А, что составляет 0.317 о. е.; If2 = 1250 А, что составляет 0.683 о. е.
Величина эквивалентного сопротивления диодного моста, питающегося от высокочастотного возбудителя, составляет RЭ1 = 0.238.
Полученное значение эквивалентного сопротивления меньше одной трети, следовательно, диодный преобразователь работает в режиме 2—3. Расчеты по формулам, приведенным в табл. 5.1, дают следующие результаты: γ = 52° , b = -0.354, g= 0.52, ψ =15.7°, F(γ, ψ) = 0.219, G (γ, ψ) = -2.76.
Коэффициенты и постоянные времени, определенные по формулам (5.15), равны: T1 = 0.739 с, Т2 = 0.286 с, k1 = 1.79, k2 = 0.795.
Параметры, входящие в уравнение (5.23), равны: A1 = 1.61, А2 = 0.593, А3 = 0.714, τ1 = 0.691, τ2 = 0.268.
Таким образом, уравнение высокочастотной системы возбуждения турбогенератора ТВФ-120-2 для номинального режима работы имеет вид:
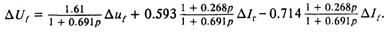
Очевидно, что для высокочастотных систем возбуждения, выполненных без силового компаундирования, выражения для параметров, входящих в уравнение (5.23), упростятся. Действительно, отсутствие трансформаторов компаундирования эквивалентно тому, что Xs → ∞, Xμ → 0.
В этом случае RЭ2 →∞, A1 = k1, А2 = 0, A3 = k2, τ1 = T1, τ2 = T2. Таким образом, математическое описание работы модернизированной высокочастотной системы возбуждения без силового компаундирования совпадает с моделью бесщеточной системы возбуждения.
Глава 6
СПОСОБЫ ПОВЫШЕНИЯ НАДЕЖНОСТИ И ЭФФЕКТИВНОСТИ РЕГУЛИРОВАНИЯ ВОЗБУЖДЕНИЯ
6.1. Методика и устройство
для проверки и наладки
систем регулирования возбуждения
Надежная и устойчивая работа генерирующего агрегата в значительной степени зависит от качества настройки системы автоматического регулирования возбуждения. Повышение требований к показателям надежности соответственно увеличивает время, необходимое на проверку, настройку и испытания систем регулирования возбуждения в период выполнения пусконаладочных работ и планово-предупредительных ремонтов. Однако технические условия эксплуатации силового энергетического оборудования ограничивают объем и продолжительность испытательных режимов. Так, например, существенные ограничения накладываются на режим холостого хода турбогенераторов, в то время как наладка систем возбуждения требует вращения турбоагрегата с номинальным числом оборотов. Значительные ограничения испытательных режимов накладываются на проверки, связанные с перегрузкой основного энергетического оборудования. В связи с этим становится эффективным специализированное устройство для проверки регулятора возбуждения (УПР), позволяющее проводить наладку и испытания регуляторов в предпусковой период на неподвижном агрегате. УПР обеспечивает повышение надежности работы системы возбуждения за счет:
— повышения устойчивости работы синхронных генераторов вследствие выполнения более качественной настройки АРВ;
— исключения опасных режимов при проведении испытаний и сокращения объема испытаний на работающем агрегате;
— снижения времени восстановления при выходе из строя блоков основного комплекта АРВ.
С помощью УПР проверяется функционирование каналов регулирования по отклонению и первой производной напряжения статора, по первой производной тока ротора, по изменению и первой производной частоты напряжения статора, а также канала жесткой обратной связи по напряжению ротора (для бесщеточных и высокочастотных систем возбуждения). УПР обеспечивает проверку работоспособности каналов ограничения максимального и минимального возбуждения, алгоритмов начального возбуждения и разгрузки генератора по реактивной мощности. Устройство представляет собой аналоговую модель синхронного генератора с системой возбуждения для ряда характерных с точки зрения проверки АРВ режимов работы
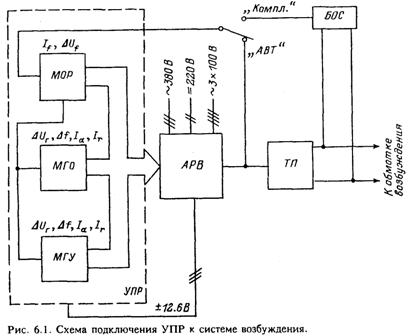
и состоит из следующих четырех блоков: блока модели объекта регулирования (МОР), блока модели генератора в режиме перевозбуждения (МГУ), блока модели генератора в режиме потребления реактивной мощности (МГО), блока модели регулятора возбуждения (МРВ).
Блок МОР является простейшей аналоговой моделью системы возбуждения и синхронного генератора, работающего в режиме холостого хода. Возбудитель моделируется в соответствии с уравнениями математической модели статической или бесщеточной системы возбуждения. В основе модели синхронного генератора лежат уравнения Парка—Горева, записанные для режима холостого хода.
С помощью блока МОР можно проверить как соединенный с возбудителем регулятор возбуждения (режим комплексной проверки), так и собственно АРВ (режим автономной проверки). В первом случае на вход блока МОР подается сигнал, пропорциональный напряжению тиристорного преобразователя, через устройство гальванической развязки, которым может служить блок обратной связи (БОС) (рис. 6.1). Во втором случае на вход блока МОР поступает выходное напряжение АРВ. На выходе блока МОР формируются сигналы, пропорциональные напряжению статора Uг и его отклонению от номинального значения ΔUг, напряжению Uf, и току If ротора, с заданными масштабными коэффициентами. Сигналы с выхода МОР подают-
8*
ся на вход блоков АРВ в качестве сигналов регулирования. Таким образом, с помощью блока МОР имитируется работа системы регулирования в замкнутой схеме, что позволяет:
— определить статические характеристики и коэффициенты передачи системы регулирования возбуждения;
— проверить устойчивость работы в режиме холостого хода генератора и определить границы областей устойчивости в координатах коэффициентов усиления каналов регулирования по первым производным напряжения статора и тока ротора при различных коэффициентах усиления каналов регулирования по отклонению напряжения и канала ЖОС (для бесщеточных и высокочастотных систем);
— проверить диапазон и скорость изменения уставки напряжения;
— проверить работу канала начального возбуждения;
— испытать в режиме автономной проверки работоспособность ограничителя двойного тока, проверить настройку характеристики ограничителя перегрузки, проверить работу ограничителя номинального тока ротора.
Наиболее характерными режимами синхронного генератора в сети с точки зрения проверки работоспособности АРВ является работа в зоне искусственной устойчивости и работа с потреблением реактивной мощности. Автоматический регулятор возбуждения, проверенный в полном объеме в этих двух крайних режимах, обеспечит высокое качество регулирования во всех остальных промежуточных режимах. Работа синхронного генератора в указанных режимах моделируется блоками МГУ и МГО.
Блок МГУ представляет собой простейшую аналоговую модель синхронного генератора, работающего с номинальной мощностью на приемную систему бесконечной мощности через дальнюю линию электропередачи, с фазовым углом между его поперечной осью и вектором напряжения шин приемной системы, превышающим 90°. Блок МГО является аналоговой моделью генератора, работающего с номинальной активной мощностью в режиме потребления реактивной мощности, с фазовым углом близким к 90°. Блоки МГУ и МГО учитывают инерционность обмотки возбуждения, механическую инерцию ротора и турбины, реакцию якоря генератора. В основе аналоговых моделей синхронного генератора лежат линеаризованные уравнения Парка—Горева. На вход блоков МГУ и МГО подается сигнал с блока МОР, пропорциональный напряжению ротора Uf, а на выходе формируются сигналы, пропорциональные отклонениям от установившихся значений напряжения статора ΔUг, частоты напряжения статора Δf, тока ротора ΔIf, а также величинам активной Ia и реактивной Ir составляющим тока статора. Выходные сигналы, сформированные с заданными масштабами, подаются на входы блоков АРВ в качестве сигналов регулирования.
Использование блоков МГО и МГУ позволяет осуществить в замкнутом контуре регулирования следующие функции:
— проверку устойчивости регулирования возбуждения в зоне ис
кусственной устойчивости и в режиме недовозбуждения с различными значениями коэффициентов усиления каналов стабилизации;
— определение границы вступления в работу ограничителя минимального возбуждения, статизма и динамику ограничителя минимального возбуждения;
— проверку работы канала разгрузки по реактивной мощности;
— проверку работы канала сгона уставки при перегрузке по току ротора.
Блок МРВ служит для проверки блоков МГУ и МГО. Необходимость в применении блока МРВ объясняется тем, что блок МГУ апериодически неустойчив, а характеристики блока МГО близки к границе колебательной устойчивости. В связи с этим определение статических и динамических характеристик этих блоков было бы без МРВ крайне затруднительно. Блок МРВ представляет собой линейную аналоговую модель регулятора АРВ-СД. На его вход поступают сигналы ΔUг, Δf, ΔIf, формируемые на выходе блоков МГУ или МГО. На выходе блока МРВ вырабатывается сигнал управления, который подается на вход блока МГУ или МГО. Таким образом проверяется работоспособность блоков МГУ и МГО в замкнутом контуре.
Опыт использования УПР на электростанциях показал его эффективность, а надежность работы и простота применения обеспечивают его широкое внедрение в эксплуатацию.
6.2. Двухканальная система регулирования возбуждения
Традиционным способом повышения надежности работы оборудования является резервирование. Большое число находящихся в эксплуатации систем возбуждения включает в себя АРВ, подключенный своим выходом ко входам двух тиристорных преобразователей (рис. 6.2), каждый из которых обеспечивает все эксплуатацион-
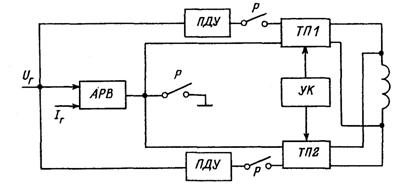
Рис. 6.2. Схема резервирования системы автоматического регулирования возбуждения.
Обозначения: АРВ — автоматический регулятор возбуждения; ПДУ — панель дистанционного управления; ТП — тиристориый преобразователь; УК — устройство контроля; Р — реле.
ные режимы работы синхронного генератора, включая работу с номинальным током и режим форсирования возбуждения. При этом предусматривается, что на обмотку возбуждения работает один преобразователь, в то время как второй находится в горячем резерве со снятыми импульсами управления. Работа преобразователей постоянно контролируется устройством контроля. При повреждении одного из преобразователей устройство контроля осуществляет отключение импульсов управления отказавшего преобразователя и переводит систему возбуждения на резервный тиристорный преобразователь.
Резервирование АРВ осуществляется включением в структуру системы регулирования панели дистанционного управления (ПДУ), представляющей собой простейший пропорциональный регулятор напряжения статора синхронного генератора. Исправность АРВ контролируется блоком контроля, входящим в состав регулятора. Перевод системы возбуждения с АРВ на ПДУ осуществляется вручную оператором или автоматически по сигналу от блока контроля, а также при отключении автоматов основного и резервного питания и автомата напряжения статора генератора.
Одним из существенных недостатков рассмотренной системы резервирования является то, что ПДУ не обеспечивает выполнения функций; возложенных на АРВ, в частности форсирования возбуждения при коротких замыканиях в энергосистеме, снижая тем самым пределы динамической устойчивости. Переходные процессы с ПДУ отличаются повышенной колебательностью по сравнению с работой на АРВ. Другим недостатком существующей схемы является отсутствие постоянного контроля за исправностью АРВ. Алгоритм работы блока контроля предусматривает его блокировку в ряде режимов, связанных с работой ограничителей перегрузки и минимального возбуждения. Кроме того, питание блока контроля осуществляется от блоков питания АРВ и, следовательно, отказ АРВ, связанный с повреждением питания, вызывает и отказ работы блока контроля.
Устранить первый из отмеченных недостатков позволяет включение в структуру резервирования второго полноценного АРВ, а второй
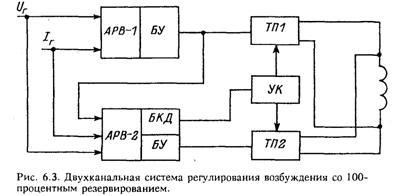
недостаток устраняется путем организации постоянного контроля исправности основного АРВ во всех эксплуатационных режимах работы генератора с помощью блока контроля и диагностики (БКД), входящего в состав резервного регулятора возбуждения. При этом схема регулирования возбуждения становится двухканальной (рис. 6.3). Основной и резервный каналы регулирования включают в себя регулятор возбуждения и тиристорный преобразователь. Оба АРВ постоянно включены, и их выходы подключены ко входам преобразователей. Тиристорный преобразователь резервного канала работает без импульсов управления. Блок БКД осуществляет постоянный контроль за исправностью основного АРВ и диагностику резервного регулятора. Кроме того, БКД обеспечивает подгонку уставки резервного АРВ с тем, чтобы уравнять выходные напряжения двух регуляторов, при этом уравнивание происходит с определенной инерцией. При возникновении неисправности резервного АРВ блок БКД своевременно диагностирует появившийся отказ и выдает команду на блокировку перехода системы возбуждения на резервный канал. При отказе основного АРВ блок БКД выдает сигналы на снятие импульсов управления тиристорного преобразователя основного канала и подачу импульсов на преобразователь резервного канала.
Работа блока БКД основана на сравнении сигналов основного (UАРВ ос) и резервного (UАРВ ос) регуляторов возбуждения. Диагностирование резервного регулятора выполняется следующим образом. На аналоговых элементах производится определение величины интеграла
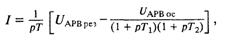
где 1/р — оператор интегрирования.
Абсолютная величина вычисленного значения интеграла сравнивается с заданной величиной. Значение абсолютной величины интеграла, превышающее заданную величину, т. е. | I | > А, свидетельствует об отказе резервного регулятора. Действительно, при наличии подгонки его уставки интеграл I стремится к нулю. Существенное его отличие от нуля указывает на то, что в течение определенного
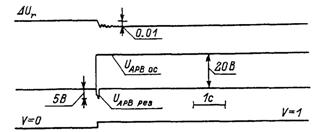
Рис. 6.4. Динамика работы блока БКД при неуправляемом развозбуждении основного АРВ.
времени выходные напряжения регуляторов не равны между собой. В свою очередь это указывает на отказ резервного АРВ.
Отказ основного АРВ определяется наличием существенной разности между выходными напряжениями основного и резервного регуляторов при отсутствии дисперсии выходного сигнала основного регулятора и при исправности резервного регулятора, т. е. неисправность основного АРВ определяется следующими условиями:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 |



