нальным регулятором возбуждения при K0u = 25-50 e. в.н./е. н. и должны оснащаться АРВ сильного действия. Машины малой и средней мощности работают в узлах нагрузки и соотношение Xвн/Xd у них меньше. Поэтому со стабилизацией их режима может справиться и пропорциональный регулятор. Однако опасность их самораскачивания все же существует.
Влияние величины переходного сопротивления X'd, сильно влияющего на массогабаритные показатели, можно оценить по значению асимптоты Θa (2.9). На рис. 2.9 приведены зависимости Θa(X'd) для ТВВ-1000-4 и ТВВ-320-2, наиболее сильно отличающихся по величине Xd при крайних реально возможных значениях Хвн. Все кривые выходят из одной (физически не реализуемой) точки Θa = 90°, X'd = 0, имеют падающий характер и пересекают ось абсцисс в точках
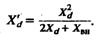
Удобно рассматривать зависимость асимптоты для всех типов генераторов от параметра b= X'd / Xd (рис. 2.10). Тогда в диапазоне 0.13<b<0.2 кривые практически совпадают друг с другом и с нормированной зависимостью
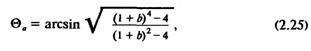
полученной из (2.9) в предположении, что Uг = Uс = 1 и Xвн = X'd, и на которую влияют только параметры проектируемой машины. Вследствие чего она может быть использована для их выбора на стадии проектирования.
Из сказанного следует, что:
— для турбогенераторов обычного исполнения в области физически реализуемых значений Х'd асимптота угла при пропорциональном регулировании напряжения с большими коэффициентами практически не зависит от величины реактивности связи с системой;
— при оценке влияния параметров турбогенератора на условия статической устойчивости и выборе типа АРВ (пропорциональный или сильного действия) целесообразно пользоваться нормированной зависимостью (2.23) или ее линейной аппроксимацией в диапазоне 0.13<b<0.2:
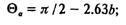
— чем больше значение синхронной реактивности проектируемого генератора, тем большие значения переходного сопротивления X'd можно допустить, не снижая уровня статической устойчивости.
Глава 3
СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ
РЕГУЛИРУЕМОЙ СИНХРОННОЙ МАШИНЫ
3.1. Экспресс-метод оценки статической устойчивости
Описанный в предыдущей главе способ определения предельно допустимых коэффициентов усиления по напряжению при различных законах регулирования возбуждения позволяет косвенно оценить уровень устойчивости в конкретном режиме электропередачи. Однако расчеты необходимо повторять при любом изменении режима, а результаты постоянно сравнивать друг с другом. В то же время диспетчерские управления, как правило, задают электростанциям уровни напряжения и величину отдаваемой активной мощности. Персоналу важно иметь перед глазами наглядную картину границ устойчивой работы станции при заданном напряжении на отправных шинах. Для построения областей устойчивости удобно пользоваться диаграммами P-Q или Ia - Ir, в которых можно строить так называемые области допустимых режимов и области рабочих режимов [9 ]. При этом координаты Ia - Ir удобнее, так как в этом случае диаграммы меньше зависят от изменения напряжения на зажимах машины.
Номинальным значениям напряжения, токов статора и возбуждения (или эдс Еq) машины, как следует из уравнения установившегося режима, соответствуют в системе о. е. выражения:
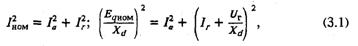
представляющие собой уравнения окружностей, первая из которых, с центром в начале координат, определяет геометрическое место точек, соответствующих номинальному току статора, а вторая, с центром в точке {Ia=0; Ir=-Uг/Xd}, — геометрическое место точек, соответствующих номинальной эдс (току возбуждения) машины. Общее множество, образованное этими окружностями, заштриховано на рис. 3.1 и представляет собой совокупность режимов, в которых может работать данная синхронная машина. (Во всех точках этого множества токи и напряжения в обмотках машины не превышают номинальных значений). При этом верхняя полуплоскость (Ia > 0) соответствует генераторному режиму работы, нижняя (Ia < 0) — двигательному, а ось абсцисс (Ia =0) — режиму синхронного компенсатора. Значения Ir > 0 соответствуют режимам генерации реак-
![]()
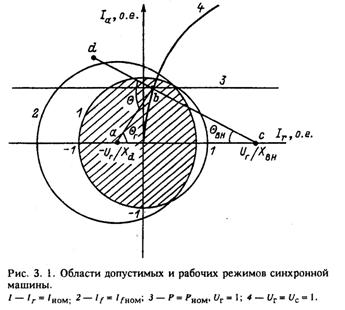
тивной мощности, значения Ir < 0 — ее потреблению из сети. Это пространство называют областью допустимых режимов [9 ].
Непосредственно из уравнений установившегося режима следует, что угол ![]() cab, образуемый осью абсцисс и лучом, проведенным из точки {Ia =0; Ir =-Uг/Xd}, является внутренним углом генератора Θвн между векторами Eq и Uг, а угол
cab, образуемый осью абсцисс и лучом, проведенным из точки {Ia =0; Ir =-Uг/Xd}, является внутренним углом генератора Θвн между векторами Eq и Uг, а угол ![]() abd, образуемый осью абсцисс и лучом из точки Uг/Xвн, — внешним углом Θвн между векторами Eq и Uс. Угол
abd, образуемый осью абсцисс и лучом из точки Uг/Xвн, — внешним углом Θвн между векторами Eq и Uс. Угол ![]() abd, лежащий между первым лучом и продолжением второго, равен полному углу электропередачи Θ между векторами Eq и Uс. Таким образом, диаграмма позволяет представить графически любой режим.
abd, лежащий между первым лучом и продолжением второго, равен полному углу электропередачи Θ между векторами Eq и Uс. Таким образом, диаграмма позволяет представить графически любой режим.
Режим синхронной машины в общем случае может меняться произвольно. Однако опыт эксплуатации показывает, что для турбогенераторов наиболее часто встречающимися вариантами изменения режима являются два:
а) изменение реактивной мощности в процессе нормальной эксплуатации; при этом активная мощность и активный ток постоянны, а изменение режима происходит в результате изменения модуля Uс при изменении режима работы потребителей или Uг при изменении уставки регулятора напряжения (рис. 3.1, прямая 3);
б) изменение активной и реактивной мощностей при Uг = const, Uс = const в процессе набора или снижения активной мощности генератора (кривая 4).
Анализируя влияние параметров и регулирования на устойчивость, мы чаще всего будем рассматривать именно эти случаи.
Если бы не было ограничения по условиям статической устойчивости, то все заштрихованное пространство было бы одновременно областью рабочих (или устойчивых) режимов. Однако в связи с ограничениями по условиям устойчивости область рабочих режимов может оказаться меньше области допустимых режимов. Следовательно, необходимо каким-то образам нанести на диаграмму границы статической устойчивости при различных законах регулирования. Тогда можно будет мгновенно дать ответ на вопрос об устойчивости и допустимости любого режима. Именно эту задачу и решает разработанный экспресс-метод.
3.1.1. Границы апериодической устойчивости
Как известно, предельными по апериодической устойчивости являются режимы, в которых угол между точками поддержания постоянства напряжения составляет 90˚. Условием устойчивости является знакоположительность всех коэффициентов аi, характеристического уравнения (2.3). По их виду можно заметить, что от величины коэффициента усиления по отклонению напряжения К0u зависят только a1 и an:
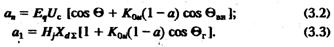
Следовательно, условия устойчивости имеют вид:
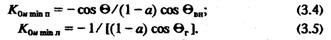
В первую очередь нарушается условие (3.4), однако, как будет показано ниже, могут возникнуть условия, при которых устойчивость будет определяться по (3.5). Поэтому при определении границы области допустимых режимов, определяемой апериодической устойчивостью, при необходимости будем учитывать и его.
После некоторых преобразований из (3.4) можно получить выражение границы апериодической устойчивости в параметрическом виде:
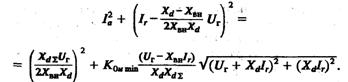
Его общее решение имеет вид:
![]()
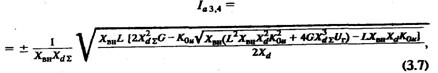
где L = Uг + XвнIr, G = Uг + XdIr. Знак «плюс» относится к генераторным режимам, «минус» — к двигательным.
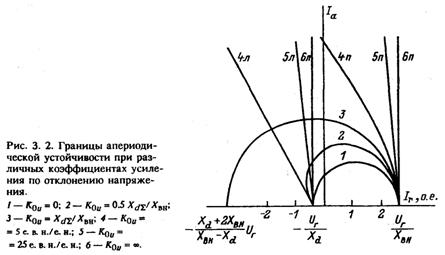
Проанализируем частные случаи для характерных значений К0u min и проиллюстрируем на рис. 3.2 полученные результаты для основного расчетного случая Xвн = 0.385 о. е.).
а) К0u min =0; нерегулируемая машина: Хp=Хd, Еq=const,
Uc= const.
Уравнение границы апериодической устойчивости вырождается в
уравнение окружности с центром в точке![]()
![]()
где
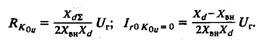
Ему соответствует на рис. 3.2 окружность 1, аналитическое выражение которой имеет вид:
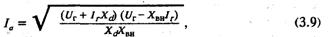
а точки пересечения с осью абсцисс соответствуют значениям
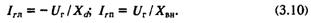
Она является геометрическим местом точек предельных режимов, в которых с помощью ручного регулирования обеспечивается ток воз-буждения, обеспечивающий заданное напряжение Uг (Еq = const). Угол между точками постоянства Еq и Uc Θ = 90°, так как опирается на диаметр окружности.
![]()
В этом и во всех последующих случаях регулятор по каналу ΔU обеспечивает постоянство эдс Ер в точке, электрически расположенной внутри машины за сопротивлением Хр. (В случае Еq = const, Хр равнялось Хd. Величина этого сопротивления может быть определена из уравнения статики при условии ΔЕр = 0:
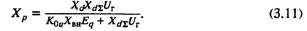
Таким образом, в каждом конкретном режиме регулируемая машина может быть замещена нерегулируемой, у которой обеспечивается постоянство эдс за сопротивлением Хр. Будем считать, что за счет ручного или медленного астатического регулирования обеспечивается одно и то же значение Uг и величина Eq в (3.11) соответствует этому значению. Отсюда следует, что при заданном коэффициенте усиления К0u величина Хр в общем случае не постоянна, а зависит от параметров режима.
Границы апериодической устойчивости, определяемые (3.6), (3.7), имеют вид замкнутых кривых, аналогичных кривой 2 на рис. 3.2, и пересекают ось абсцисс в тех же точках, что и в предыдущем случае.
в) K0u min = l/(l-a)=Xd![]() /Xвн.
/Xвн.
Регулятор снова обеспечивает постоянство Ер за Хр, но величина Хр меньше, чем в предыдущем случае, и Ер электрически ближе расположена к Uг.
Из уравнения (3.2) следует, что
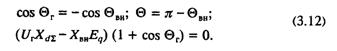
Последнее уравнение имеет два решения:
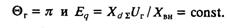
Графически им соответствуют на рис. 3.2 отрезок оси абсцисс, лежащий левее точки Ir=-Uг/Xd, и окружность 3 со смещенным относительно начала координат центром:
![]()
Она пересекает ось абсцисс в точках:
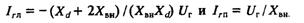
Аналитическое выражение границы в этом случае может быть получено в виде:
![]()
Область апериодической устойчивости расширяется настолько, что сползание становится невозможным при любых реальных значениях реактивной мощности. Ее граница (кроме режимов синхронного компенсатора левее точки Ir=-Uг/Xd) совпадает с границей апериодической устойчивости нерегулируемой машины, с синхронной реактивностью
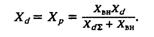
Т а б л и ц а 3.1 | ||||
Xвн | Хр | К0u | Примеч. | |
о. е. | о. е. | е. в.х. х. е. н. | е. в. н. е. н. | |
0.2 0.385 0.523 0.9 | 0.172 0.294 0.368 0.522 | 15.44 7.462 5.757 3.764 | 4.933 2.384 1.84 1.203 | Xp< Х'd Xp< Х'd Хр = Х'd Xp> Х'd |
При определенном значении внешней реактивности Хр = Хq. В нашем случае это условие выполняется при Хвн = 0.523. При такой связи с системой медленнодействующий регулятор, поддерживающий Е'q = const, будет обеспечивать апериодическую устойчивость в соответствии с (3.14). При Хр > Х'd такой регулятор будет соответствовать случаю б), при Хр < Х'd — случаю г). В табл. 3.1 приведены значения Хр и соответствующие им значения К0u, обеспечивающие постоянство Ер за Хр = const. Хотя Хр и меняется по величине, его абсолютное значение намного меньше Хd, т. е. даже медленнодействующий АРВ существенно компенсирует синхронное сопротивление.
![]()
Это наиболее интересный случай, так как реализуемые в регуляторах возбуждения значения коэффициента К0u, как правило, ле-, жат в этом диапазоне. Уравнение (3.7) имеет комплексные корни и не имеет физического смыс-
ла, уравнение (3.6) дает незамкнутую границу области апериодической устойчивости «справа», пересекающую ось абсцисс в точке Iгп = Uг/Xвн (рис. 3.2, кривые 4п, 5п). Но это вовсе не значит, что ограничения в режимах потребления реактивной мощности нет. Оно определяется выражением (3.5):
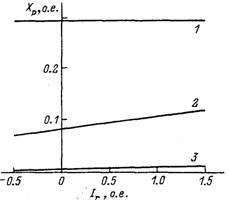
Рис.Зависимость сопротивления Хр от режима и коэффициента усиления по напряжению.
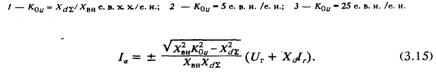
Это прямые, проходящие через точку Iгл. Их наклон зависит от величины коэффициента усиления по напряжению.
д) Кou→∞ (бесконечно большой коэффициент усиления).
Границы «слева» и «справа» превращаются в вертикальные прямые 6л, и 6п, проходящие через характерные точки Irл, Irп, причем правая соответствует пропускной способности электропередачи в режимах выдачи реактивной мощности.
На рис. 3.3 показано, как зависит величина сопротивления Хр, за которым сохраняется постоянство эдс, от режима и К0u.
Таким образом, при реальных значениях коэффициента К0u область апериодической устойчивости при перевозбуждении (Q > 0) ограничена справа режимами, в которых угол между Ер и Uc достигает 90°. При реальных значениях 0.2 ≤ Хвн ≤ 0.5 о. е. это ограничение лежит намного правее области допустимых режимов и его можно не учитывать. В режимах потребления реактивной мощности (Q < 0) апериодическая устойчивость нарушается при превышении внутренним углом между Ер и Uг значения 90°. Эта левая граница существенно ограничивает область устойчивых рабочих режимов. Однако при конечных значениях K0u устойчивы режимы, лежащие левее прямой Ir=-Uг/Xd, которую до сих пор всегда считали пределом апериодической устойчивости синхронной машины обычного исполнения в режимах потребления [9 ]. Расширение области тем больше, чем меньше величина К0u. Поэтому с точки зрения апериодической устойчивости целесообразно снижение этого коэффициента.
3.1.2. Границы электромеханической
колебательной устойчивости
Выражение для максимально допустимого по условиям устойчивости низкочастотного внешнего электромеханического движения коэффициента усиления по напряжению
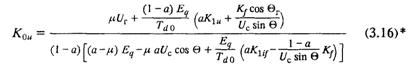
накладывает дополнительные ограничения на область допустимых режимов. Оно было получено при допущении о безынерционности каналов регулирования регулятора.
Рассмотрим сначала случай регулирования только по отклонению напряжения и его производной (K1if = Kf = 0).
После ряда преобразований (3.16) приводится к виду
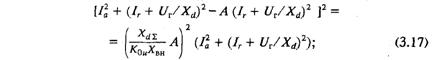
где
![]()
математически описывающему кривую, получившую название «улитки» [35 ]. После замены переменных Ir+Uг/Xd=X интересующее нас решение уравнения 4-й степени получим в виде
![]()
Знак «плюс» соответствует генераторному режиму, знак «минус» — двигательному.
 * Для гидрогенератора выражение (3.16) имеет вид:
* Для гидрогенератора выражение (3.16) имеет вид:
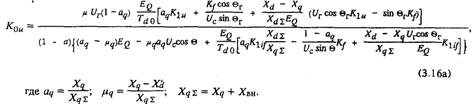
Нетрудно заметить, что при Xq = Xd (турбогенератор) оно полностью совпадает с (3.16).
На рис. 3.4 приведены границы колебательной устойчивости при К0u = 25 e. в.н./е. н. для трех различных значений K1u, а на рис. 3.5 — то же при К0u = 5 е. в.н./е. н. Видно, что все они пересекают ось абсцисс слева в точке Irл=-Uг/Xd, а правая точка пересечения Irп, зависит от величины коэффициентов К0u и К1u:
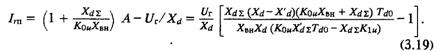
![]() При Кou→∞ уравнение границы вырождается в окружность (3.8)
При Кou→∞ уравнение границы вырождается в окружность (3.8)
радиуса с центром в точке
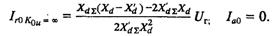
Построение границы колебательной устойчивости по уравнению (3.18) требует применения вычислительной техники и специализированных программ. Поэтому для инженеров, не располагающих ими, можно предложить предельно простой способ построения границы по четырем точкам.
Из (3.17) следует, что значению Х = 0 (Ir=-Uг/Xd) соответствуют два значения активного тока:
![]()
При Ia3 = 0 определяется третья точка (3.19). Четвертую точку (экстремум) кривой найдем, взяв частную производную выражения (3.18) по реактивному току ![]() и приравняв ее нулю:
и приравняв ее нулю:
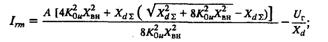
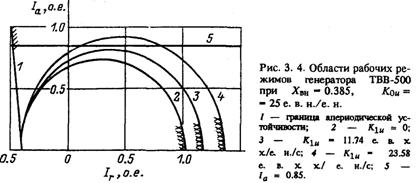
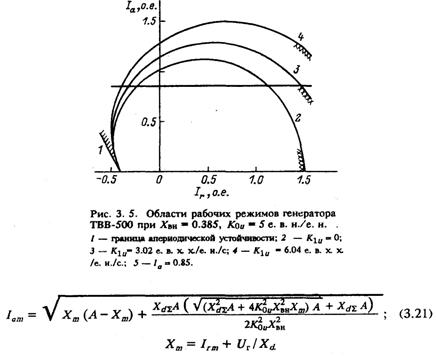
Нанеся эти четыре точки на диаграмму рабочих режимов и соединив их между собой плавной выпуклой кривой, можно довольно точно построить границу колебательной устойчивости для простейшего закона регулирования возбуждения.
3.1.3. Рекомендации по применению
Полученные выше соотношения дают возможность без применения специализированных программ нанести на диаграмму режимов синхронной машины границы апериодической и колебательной статической устойчивости при регулировании возбуждения по отклонений и по первой производной напряжения генератора. Исходными данными служат параметры исследуемого генератора или эквивалентного генератора станции и значение Хвн. Порядок расчетов следующий:
1. Выбираются предполагаемые значения коэффициентов усиления K0u [е. в.х. х./е. н. ] и K1u [е. в.х. х./е. н./с].
2. Строится диаграмма допустимых режимов в координатах
Ia - Ir.
3. Выбираются предполагаемые значения уровней напряжения по концам эквивалентной электропередачи.
4 ,
4. Сравнивается выбранное значение К0u с величиной Xd![]() /Xвн;
/Xвн;
при К0u > Xd![]() /Xвн (наиболее часто встречающийся случай) наносятся на диаграмму границы «справа» по уравнению (3.6) и «слева» — по уравнению (3.15).
/Xвн (наиболее часто встречающийся случай) наносятся на диаграмму границы «справа» по уравнению (3.6) и «слева» — по уравнению (3.15).
5. Строится по уравнению (3.18) граница колебательной устойчивости. Если выполнить полный объем вычислений затруднительно, то ее построение выполняется приближенно по четырем точкам (3.19)—(3.21).
В результате получим область рабочих режимов, представляющую собой внутреннюю часть построенных областей. Анализируя ее (рис. 3.4 и 3.5), можно решить, справится ли пропорциональный регулятор со стабилизацией всех возможных режимов, следует ли уменьшать коэффициент усиления по напряжению или предусмотреть сильное регулирование возбуждения. При этом нужно иметь в виду, что для обеспечения приличного качества регулирования необходимо иметь запас устойчивости в каждом из режимов.
Все эти задачи, а также задачу выбора коэффициента Kf, обеспечивающего требуемое значение К0u max, можно решать в полуавтоматическом режиме с помощью ППП «Модель».
3.2. Статическая устойчивость
при включенных каналах стабилизации
Ранее мы получили границы статической устойчивости при регулировании по отклонению и производной напряжения. Реализуемый в российских регуляторах закон регулирования (1.19) включает в себя дополнительно к отклонению и производной напряжения сигналы стабилизации по производной тока возбуждения, а также по отклонению и первой производной частоты напряжения генератора. В разд. 2.3 было показано, что безынерционный сигнал I'f отрицательно сказывается на устойчивости и в реальных регуляторах вводится его запаздывание. Положим, что W1if =1/(1+рτ), τ =0.15с. Совместное действие каналов стабилизации «по частоте» по-прежнему будем учитывать безынерционным сигналом Δfu, вводимым с эквивалентным коэффициентом kf= 0.5K0f [е. в.х. х./рад/с ] (К0f[дел] = К1f[дел]).
В этом случае порядок характеристического уравнения повышается и его коэффициенты имеют вид:
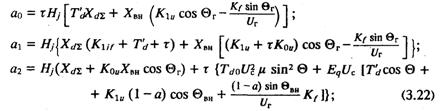
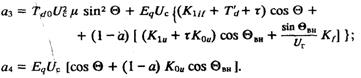
На апериодическую устойчивость каналы производных не влияют. Ее границы по-прежнему определяются выражениями (3.6), (3.15). Границу колебательной устойчивости получим, приравняв нулю предпоследний определитель системы

Аналитическое решение этого уравнения очень громоздко. Поэтому остается только одна возможность: решить его численным методом.
Воспользовавшись вытекающими из уравнений установившегося режима выражениями:
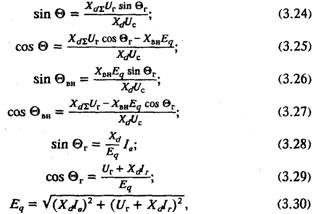
исключим из (3.23) все переменные, кроме активного и реактивного токов, и получим полное уравнение 9-й степени относительно Ia и Ir. Подставив в него параметры электропередачи и величину напряжения генератора, решим любым численным методом, например методом Ньютона, и получим для выбранного числа точек границу в виде зависимости Ia(Ir). Останется только нанести ее на область допустимых режимов.
На рис. 3.6—3.8 показано для выбранного расчетного примера, как влияют сигналы стабилизации по производной тока ротора и частоте напряжения на области колебательной устойчивости при разной
величине коэффициента усиления по напряжению.
4*
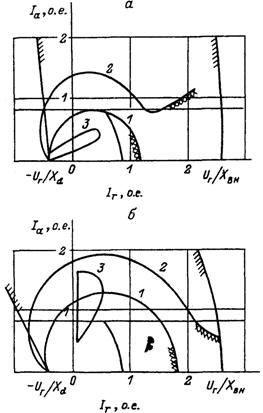
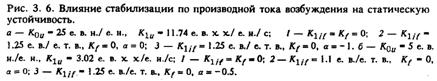
Видно, что стабилизация только «по частоте» расширяет область устойчивости в режимах перевозбуждения и практически не помогает в режимах потребления реактивной мощности. Сигнал I'f, наоборот, помогает в режимах потребления, а в режимах выдачи Q его эффективность падает. Совместное действие всех каналов стабилизации позволяет получить практически одинаковый запас устойчивости в режимах Р = Pном, Q = var.
До сих пор мы рассматривали границы устойчивости, то есть линии нулевого затухания. Однако существует возможность нанести на область допустимых режимов и линии равного затухания, соответствующие определенной величине вещественной части самой правой пары комплексных корней системы.
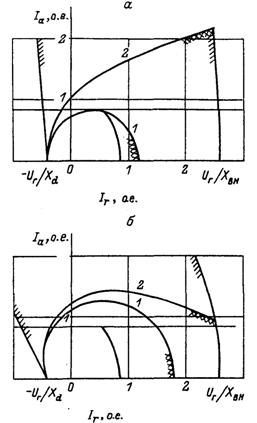
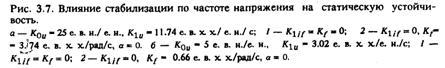
![]() Для этого нужно заменить в характеристическом уравнении (2.3) оператор р на другой, равный значению корня р = α + jω
Для этого нужно заменить в характеристическом уравнении (2.3) оператор р на другой, равный значению корня р = α + jω![]() , и получить новое характеристическое уравнение вида
, и получить новое характеристическое уравнение вида
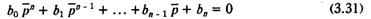
![]() с коэффициентами bi = f(α, αi), i = 1 ... n. Тогда условие Δn-1 = 0 определит линию равного затухания с заданной величиной вещественной части корня α. В нашем конкретном случае
с коэффициентами bi = f(α, αi), i = 1 ... n. Тогда условие Δn-1 = 0 определит линию равного затухания с заданной величиной вещественной части корня α. В нашем конкретном случае
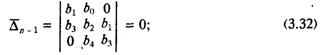
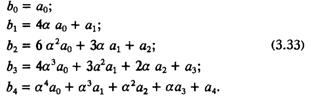
Снова исключив промежуточные переменные, получим полное уравнение 18-й степени относительно Ia, Ir и α. Численно решив его, получим область равного затухания при заданном значении α, а следовательно при равном времени затухания переходного процесса
Т ![]() 3/ α [8 ]. Эти линии показаны на рис. 3.6, 3.8.
3/ α [8 ]. Эти линии показаны на рис. 3.6, 3.8.
Для подтверждения полученных результатов на рис. 3.9, 3.10 приведены переходные процессы, выполненные с помощью ППП «Модель» при точном моделировании динамических свойств регуляторов и возбудителей. Видно, что при настройках, выбранных по изложенной методике, качество регулирования оказывается именно таким, как предполагалось.
Очень важным результатом является тот факт, что при снижении коэффициента усиления по напряжению возрастает эффективность сигналов U' и I'f. Значит, спроектировав регулятор таким образом, чтобы на нулевой частоте (в установившемся режиме) он имел большой или вообще бесконечный коэффициент усиления по напряжению, а при возникновении колебаний работал как пропорциональный регулятор с коэффициентом усиления ![]() 5 е. в.н./е. н., можно для большинства генераторов и станций обеспечить стабилизацию режима без введения сигналов по частоте напряжения генератора и ее производной.
5 е. в.н./е. н., можно для большинства генераторов и станций обеспечить стабилизацию режима без введения сигналов по частоте напряжения генератора и ее производной.
Еще одним аргументом в пользу снижения пропорционального коэффициента усиления по напряжению служит значительное расширение области апериодической устойчивости в режимах потребления реактивной мощности. Ранее считалось [9 ], что синхронная машина обычного исполнения принципиально не может устойчиво работать в режимах потребления при Q < - U2г/Xd единственной альтернативой является асинхронизированный генератор. Более точный анализ показывает, что снижение К0u позволяет полностью использовать конструктивные возможности генераторов обычного исполнения в режимах потребления.
Эти положения и были взяты за основу при проектировании описанного в последующих разделах регулятора АРН, уже вошедшего в серийное производство для машин малой и средней мощности.
По результатам приведенных в этой главе материалов может сложиться впечатление о целесообразности максимального увеличения коэффициентов по каналам стабилизации, так как в этом случае области статической устойчивости могут быть сколь угодно расширены. Однако на самом деле это не так. Проводя анализ влияния параметров стабилизации на устойчивость, мы сделали предположение о безынерционности всех элементов системы регулирования,
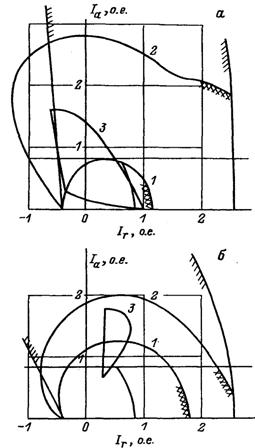
Рис. 3.8. Совместное влияние стабилизации по производной тока возбуждения и частоте напряжения на статическую устойчивость.
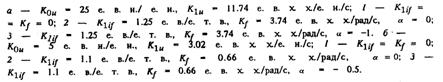
кроме особо оговоренных случаев. В реальной системе регулирования эта инерционность неизбежна. Она сказывается на величине фазовых сдвигов при росте частоты колебаний. В результате появляется опасность так называемой высокочастотной неустойчивости электромагнитных контуров, которая до сих пор не учитывалась и которая практически не сказывается на внешнем движении генератора, но приводит к высокочастотным колебаниям напряжения возбуждения, что явно недопустимо.
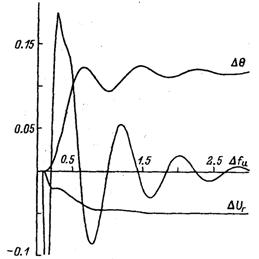
Рис. 3.9. Затухание малых колебаний при точном моделировании АРВ и возбудителя.
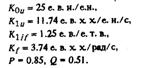
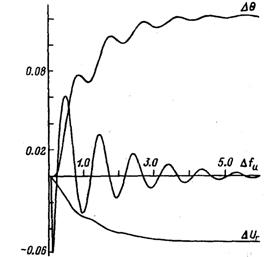
Рис. 3.10. Затухание малых колебаний при точном моделировании АРВ и возбудителя.
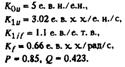
Анализ этого вида неустойчивости требует подробного математического описания АРВ и возбудителя с подробным учетом даже малых постоянных времени. Именно этим вопросам посвящены две следующие главы.
3.3. Внутригрупповое движение
В процессе развития энергетики предлагались различные способы формирования сигналов стабилизации АРВ как в виде комбинаций местных параметров, так и с использованием телеметрической информации. В 70-х годах в СССР этим исследованиям уделялось большое внимание. Все предложения обсуждались на семинарах по кибернетике электрических систем, а затем проверялись расчетным путем и на электродинамических моделях. Это позволяло избежать субъективности в оценках.
Очень многие из предложенных параметров улучшали устойчивость внешнего движения, но не могли быть рекомендованы к внедрению из-за отрицательного влияния на внутригрупповое движение генераторов многомашинной станции. Рассмотрим влияние различных параметров стабилизации на устойчивость внутригруппового движения, воспользовавшись полученной в гл. 1 структурной схемой объекта регулирования (см. рис. 1.5). Схема подтверждает правильность полученного ранее вывода о том, что «если стабилизация всех генераторов производится по одному общему параметру, то область устойчивости внутригруппового движения занимает всю плоскость в координатах стабилизирующего параметра и общая область устойчивости определяется основным движением» [31 ]. Такими общими параметрами являются напряжение генератора и частота напряжения. Индивидуальные параметры по-разному влияют на внутригрупповое движение.
Стабилизация «по току»
В самой первой модификации АРВ (для Куйбышевской ГЭС) предусматривалась стабилизация по первой и второй производным тока статора. В этом случае
![]()
Учитывая, что S2г = P2г + Q2г = (UгIг)2, после линеаризации получим:
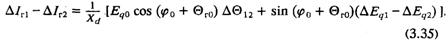
Таким образом, стабилизация «по току» может быть представлена в виде совместного действия двух составляющих:
первой — гибкой внешней отрицательной обратной связи по отклонению взаимного угла, наиболее интенсивной при нулевой активной нагрузке, когда Θг0→0, ослабляющейся по мере роста Θг0 и уменьшения реактивной мощности; эта обратная связь никогда не может стать положительной, так как косинус — четная функция;
второй — гибкой внутренней положительной обратной связи по разности отклонений токов возбуждения; отрицательной
она может стать только в режиме синхронного компенсатора, работающего с потреблением реактивной мощности (Θ![]() 0, sinφ ≤ 0).
0, sinφ ≤ 0).
Наличие этой обратной связи приводит к появлению незатухающих колебаний в электромагнитных контурах генераторов. Именно по этой причине в АРВ Куйбышевской ГЭС пришлось перейти на стабилизацию по производным общего параметра — суммарного тока линий, а в дальнейшем — на стабилизацию по частоте эдс.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 |



