На основании системы (1.8)—(1.9), дополненной уравнением регулирования (1.27), можно построить обобщенную структурную схе-
му системы автоматического регулирования возбуждения (САУВ) синхронного генератора для внешних колебаний (рис. 1.7).
С помощью этой схемы и будет проведен анализ статической устойчивости синхронной машины при различных законах регулирования на примере турбогенератора, поскольку в этом случае все особенности регулирования сохраняются, а математические выражения существенно упрощаются. При необходимости читатель может распространить полученные в данной книге результаты на случай гидрогенератора.
Глава 2
ПРЕДЕЛЬНО ДОПУСТИМЫЕ КОЭФФИЦИЕНТЫ УСИЛЕНИЯ ПО ОТКЛОНЕНИЮ НАПРЯЖЕНИЯ
2.1. Условия устойчивости
Исторический обзор развития и совершенствования систем возбуждения приведен в [33 ]. Первоначально основной задачей систем автоматического управления возбуждением (САУВ) считалось поддержание напряжения регулируемых генераторов, причем требования к точности были невысоки, и с этой задачей успешно справлялись АРВ пропорционального действия. Характеристики мощности систем с пропорциональным регулированием возбуждения и их особенности рассмотрены в [34]. Основной регулируемой координатой в этих регуляторах является отклонение напряжения на зажимах генератора. САУВ этого типа и сейчас используются на станциях малой и средней мощности, однако в ряде случаев возникают трудности с обеспечением их статической устойчивости. Для того чтобы уяснить причины возникновения колебаний, рассмотрим, как влияет на устойчивость величина коэффициента усиления по отклонению напряжения К0u. При этом, исследуя малые колебания, в дальнейшем будем опускать индекс «0» при установившихся значениях переменных.
Мощность, отдаваемая станцией в систему, пропорциональна величине напряжения на ее отправных шинах и синусу фазового угла Θвн между напряжениями на концах электропередачи (1.1). Следовательно, для увеличения передаваемой мощности следует стремиться к устойчивой работе при возможно больших значениях внешнего угла, вплоть до 90°, и к поддержанию заданного напряжения UГ в отправной точке с высокой точностью, или, что то же самое, с малым статизмом, под которым понимают величину su =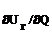 .
.
Анализ зависимости статизма от параметров САУВ является сложной задачей, но общие закономерности, показывающие пути его уменьшения и возникающие при этом трудности, можно показать на примере выбранной схемы электропередачи (см. рис. 1.2), отсеяв влияние малосущественных вторичных факторов. В этом случае ста-тизм определяется соотношением
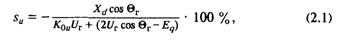
из которого видно, что он существенно зависит не только от параметров электропередачи, но и от исходного режима. При обычно применяемых значениях К0u, как правило,
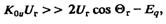
поэтому допустимо воспользоваться приближенной формулой
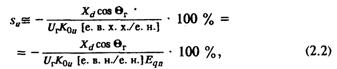
где К0u — коэффициент усиления по напряжению на нулевой частоте. Видно, что статизм, а значит и точность регулирования, сильнее всего зависят от коэффициента усиления по напряжению. Значит, для повышения точности необходимо стремиться увеличивать К0u. В то же время известно, что это может привести к возникновению колебаний в системе. Это противоречие между требованиями точности регулирования и качества демпфирования колебаний является внутренним противоречием параметра регулирования ΔU. На его преодоление были затрачены годы исследований и экспериментов.
Рассмотрим, какие предельные значения Θ, К0u и su можно обеспечить в расчетной схеме при различных алгоритмах регулирования возбуждения.
Для анализа статической устойчивости достаточно рассмотреть характеристическое уравнение структурной схемы (см. рис. 1.7)
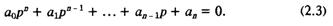
Чтобы получить не очень громоздкие и поддающиеся анализу выражения, пренебрежем демпферным моментом в передаточной функции Wрот (1.10). Это допущение утяжеляет условия устойчивости, и можно считать, что получаемая разница идет в инженерный запас. Кроме того, в данном разделе примем еще одно допущение о безы-нерционности элементов регулятора возбуждения, т. е. положим в уравнении регулирования (1.19) Wif = Wf = 1.
Тогда получим характеристическое уравнение третьего порядка с коэффициентами:
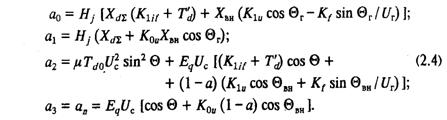
Условия устойчивости по [8 ]:
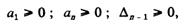
|
где — предпоследний определитель, составлен- |
ный из коэффициентов характеристического уравнения. Размерности коэффициентов: К0u [е. в. х. х./е. н. ], К1u [е. в. х. х./е. н./с], К1if [е. в. х. х./е. т. в./с], kf [е. в. х. х./рад./с]. Для перевода величин коэффициентов усиления из единиц холостого хода в номинальные необходимо разделить их на отношение Ifн/Ifхх т. е. на Еqn.
Первое условие при реальных значениях параметров и коэффициентов регулирования выполняется всегда, второе — при
К0u≥К0umin. В случае нарушения неравенства происходит апериодическое нарушение устойчивости [8, 11 ]. Таким образом, величина Koumin определяет предел по сползанию. Третье условие выполняется при К0u < К0umax. В случае его нарушения возникает так называемая колебательная неустойчивость. Выражения для предельно допустимых значений коэффициента усиления по напряжению можно получить в виде:
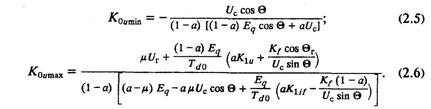
Проанализировав их, можно уяснить влияние различных факторов на устойчивость. Рассмотрим несколько вариантов закона регулирования в порядке их усложнения.
2.2. Пропорциональное регулирование
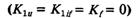
Граница по сползанию имеет вид (2.5), а условие колебательной устойчивости упрощается:
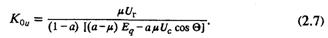
На рис. 2.1 показано, как при пропорциональном регулировании предельные коэффициенты зависят от режима электропередачи. Область допустимых режимов ограничена снизу кривой АВС. Выход за нее означает появление положительного вещественного корня (апериодическое нарушение устойчивости). Сверху область ограничена кривой DBE, выход за которую означает наличие двух комплексных сопряженных корней с положительной вещественной частью (колебательная неустойчивость).
Можно отметить некоторые важные, используемые в дальнейшем при анализе параметров генератора на устойчивость, значения полного угла Θ и соответственно мощности Р.
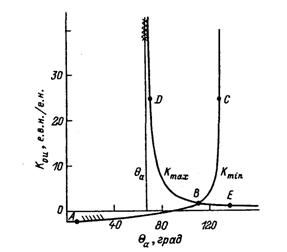
Рис.Предельно допустимые коэффициенты усиления по напряжению при пропорциональном регулировании.
2.2.1. Предел колебательной устойчивости при больших значениях коэффициента регулирования по напряжению
Этот предел характеризуется асимптотой кривой DBE при значении Θ = Θа (см. рис. 2.1), когда обращается в ноль знамена:
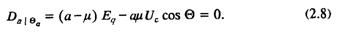
После ряда преобразований получим отсюда выражение, определяющее величину асимптомы Θа в зависимости только от параметров исследуемой энергосистемы и от уровней напряжения в начале и конце эквивалентной линии:
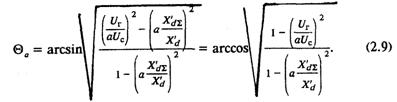
Левее этой границы самораскачивание невозможно.
Поясним физическую сущность этого положения. Положим, что
вследствие некоторых причин угол Θ совершает малые колебания с
частотой hω0 и амплитудой ΔΘm, т. е.
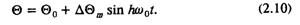
Выбранный закон движения ротора в известной степени имитирует начальное движение ротора при появлении апериодической или колебательной неустойчивости. Так, монотонное изменение угла получим, устремив в (2.10) частоту колебаний h к нулю и подобрав амплитуду ΔΘm, таким образом, чтобы произведение hΔΘm, при h → 0 не было тождественно нулю. Вторая, наиболее интересная при рассмотрении вопроса о качестве регулирования напряжения форма начального движения ротора дается в первом приближении непосредственно выражением (2.10) при конечной частоте колебаний h. Частота качаний синхронных машин на практике не превышает 2,5 Гц, поэтому будем считать, что частота колебаний h может принимать все значения в интервале 0—0,05.
Из-за большой самоиндукции контура ротора поток его будет отставать от изменения угла Θ, заданного выражением (2.10). При этом поток ротора или при соответственном выборе единиц численно
равная ему эдс E'q будут изменяться в зависимости от исходного режима для регулируемой и нерегулируемой машин по-разному. Закон изменения E'q (ΔΘ) можно найти из уравнения для обмотки возбуждения. Рассмотрим случай пропорционального регулирования напряжения, когда
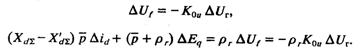
Кроме того,
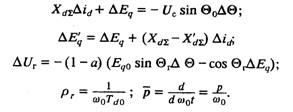
Исключая из этой системы ΔEq, Δid И ΔUГ, получим:
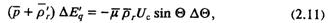
где
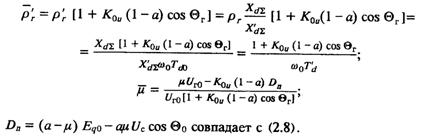
При постоянстве тока возбуждения K0u = 0, ρ'r = ρ'r, μ = μ и выражение (2.11) принимает вид
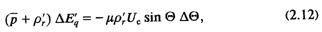
впервые полученный [1 ], подробно рассмотревшим устойчивость нерегулируемой машины. Он показал, что в этом случае раз возникшие колебания конечной частоты h не будут прогрессировать, а под действием имеющейся избыточной энергии будут затухать до нуля.
В данной работе этот подход развит применительно к регулируемой машине. При большом коэффициенте по напряжению K0u→∞ при условии, что
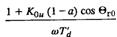
не тождественно нулю, имеем:
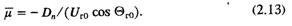
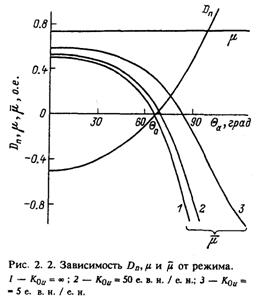
Величина μ уже не постоянна, а зависит от исходного режима. На рис 2.2 приведены зависимости Dn и μ от угла для расчетного примера; D (Θ) имеет падающий характер и обращается в ноль при величине угла Θ = Θa, определенного ранее (2.9). Очевидно, что при анализе колебательной устойчивости необходимо рассмотреть три случая.
1. Θ < Θa, Dn < 0; μ > 0.
Найдем частное решение уравнения (2.11) при выбранном законе движения ротора (2.10), т. е. значение ΔE'q после затухания его апериодической составляющей. После соответствующих выкладок найдем
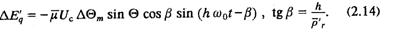
Выражение (2.14) дает изменение потока ротора во времени. Исключив время из (2.10) и (2.14), получим зависимость ΔE'q непосредственно от ΔΘ:
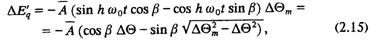
где |
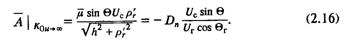
Формально полученные выражения не отличаются от рассмотрен-
ного случая нерегулируемой машины, поэтому воспользуемся для анализа его методикой.
После некоторых преобразований получим
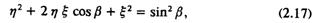
где
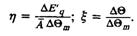
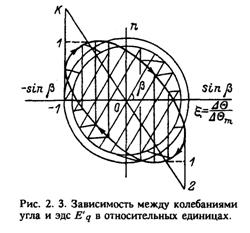
В результате преобразования координат последнее уравнение приводится к уравнению эллипса, который проще всего построить по точкам (рис. 2.3). Каждая точка эллипса соответствует в пределах одного периода колебаний 2π/hω0 определенному моменту времени. При этом, сравнивая уравнения (2.10) и (2.14), легко убедиться, что при увеличении времени t точка, изображающая ΔE'q на плоскости
(ΔE'q, ΔΘ), движется в направлении, указанном стрелками, т. е. по часовой стрелке. Следовательно, в этом случае влияние самоиндукции ротора сводится к тому, что поток ротора запаздывает в своем изменении по отношению к вызвавшим это изменение колебаниям угла Θ. Переход через ноль потока ротора происходит позже, чем при предположении о возможности применения для вычисления потока ротора уравнений установившегося режима.
Выражение активной мощности, отдаваемой машиной,
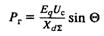
после подстановки
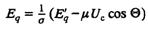
принимает следующий вид:
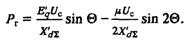
При колебаниях Θ эдс Еq в последнем выражении будет получать приращение, найденное нами выше. В соответствии с этим мгновенное значение мощности Рг при колебаниях угла Θ около своего среднего положения Θо изобразится кривой, получаемой наложением на кривую Pг при E'q = const добавочной составляющей, обязанной изменению ΔE'q. Соответствующая кривая показана на рис. 2.4, а; при изменении угла Θ изображающая точка на этой кривой вращается по часовой стрелке, как было найдено выше; прямая рр' дает величину мощности первичного двигателя, отвечающую средней мощности, отдаваемой генератором при угле Θ. Интересующий нас участок кривой мгновенной мощности показан на рис. 2.4, б. Разность ординат кривой мгновенной мощности и прямой рр' дает избыточный момент, действующий на ротор и определяющий его ускорение.
В точке а имеем ΔΘ = -ΔΘm, а относительная скорость равна нулю. Так как при этом избыточный момент, равный отрезку ра, является вращающим, то угол будет возрастать. В точке b избыточный момент и ускорение ротора равны нулю. Так как при изменении угла от -ΔΘ до этого значения ротор имеет запас кинетической энергии, пропорциональный площади фигуры аbр, то угол будет продолжать
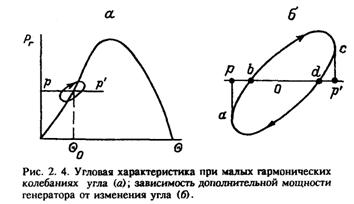
возрастать по направлению к точке с. При этом ротор расходует накопленную им энергию, причем расход энергии равен площади фигуры bср, и вследствие того что эта площадь больше площади abp, при постоянстве мощности первичного двигателя точка с не может быть достигнута, ибо площадь торможения оказывается больше площади разгона. Избыточная энергия, равная площади bcd, тормозит ротор, т, е. при увеличении угла Θ стремится его уменьшить. При заданном нами законе изменения угла последний достигнет своего значения ΔΘm, и начнет уменьшаться.
Рассматривая изменение ΔΘ от ΔΘm, до - ΔΘm, придем к выводу, что при таком движении ротора развивается добавочная энергия, равная площади dab и стремящаяся ускорить ротор, т. е. увеличить Θ. Таким образом, возникающая при движении изображаемой точки по траектории abcda избыточная энергия равна полной площади цикла и стремится изменить угол в направлении, противоположном предполагаемому его изменению. При этом условии можно полагать, что система будет устойчивой, т. е. что раз возникшие колебания не будут прогрессировать, а под действием имеющейся в данном случае избыточной энергии будут затухать до нуля [1 ].
Сравним теперь интенсивность демпфирования колебаний, пропорциональную площади цикла, при постоянстве тока возбуждения и при пропорциональном регулировании. Амплитуда колебаний потока ротора при постоянстве тока возбуждения
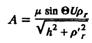
монотонно возрастает пропорционально sinΘ по мере утяжеления режима. Соответственно площадь цикла, ограниченная кривой abcda, также возрастает, и интенсивность демпфирования малых колебаний каждой конечной частоты (h > 0) с ростом нагрузки возрастает во всем рассматриваемом диапазоне 0 < Θ < Θa.
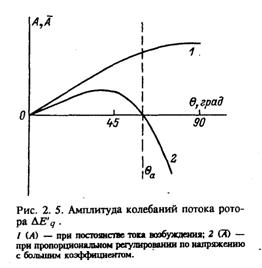
Амплитуда колебаний ΔE'q, при пропорциональном регулировании напряжения с большими коэффициентами (2.16) зависит не только от sin Θ, но и от величины Dn. Эта зависимость приведена на рис. 2.5, из которого видно, что интенсивность демпфирования малых колебаний в этом случае ниже естественной, но все же в диапазоне 0 < Θ < -Θm колебательная неустойчивость возникнуть не может. По мере роста отдаваемой мощности линия KL (рис. 2.3) и фигура abcda (рис. 2.4, б) сначала поворачиваются по часовой стрелке в направлении от оси абсцис с к оси ординат, а после достижения режима, в котором
![]() = 0 — против часовой стрелки. При этом ширина эллипсов на обоих рисунках сначала возрастает, а после изменения направления вращения линии KL уменьшается. Соответственно меняется и интенсивность демпфирования колебаний.
= 0 — против часовой стрелки. При этом ширина эллипсов на обоих рисунках сначала возрастает, а после изменения направления вращения линии KL уменьшается. Соответственно меняется и интенсивность демпфирования колебаний.
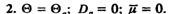
В этом режиме ΔE'q ≡ 0, E'q = const, т. е. поток ротора не зависит ни от малых колебаний угла, ни от действия регулятора напряжения. Эллипс на рис. 2.3 вырождается в отрезок оси абсцисс -1 ÷ +1, а площадь торможения abcda (рис. 2.4) — в отрезок прямой ас, совпадающий в окрестности точки Θ с зависимостью Рг(Θ). В точке а имеем:
ΔΘ = - ΔΘ ; относительная скорость равна нулю; избыточный момент, равный отрезку ра, приводит к возрастанию угла. В точке b избыточный момент и ускорение ротора равны нулю, а запас кинетической энергии пропорционален площади треугольника apb. Угол будет продолжать возрастать до точки с. Ротор расходует накопленную энергию, причем площадь торможения bср равна площади ускорения apb. Избыточная энергия, тормозящая ротор, отсутствует. При заданном нами законе изменения угла последний достигнет максимального значения ΔΘm = │-ΔΘm│ и начнет уменьшаться. При движении ротора от ΔΘm, в сторону уменьшения угла процесс протекает аналогично и, поскольку избыточная энергия, ускоряющая ротор, отсутствует, будет достигнуто значение - ΔΘm. Система находится на границе устойчивости, т. е. раз возникшие колебания будут существовать бесконечно долго.
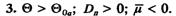
До достижения этого режима размагничивающее действие реакции якоря при росте нагрузки преобладало над намагничиванием, обусловленным регулированием напряжения, и эдс E'q уменьшалась с ростом угла. После точки Θa намагничивающее действие регулятора напряжения преобладает над действием реакции якоря, и с увеличением угла эдс E'q увеличивается. Изменение потока ротора во времени по-прежнему описывается уравнением (2.14), однако при больших коэффициентах усиления амплитуда колебаний потока ротора Ā (выражение (2.16) и рис. 2.5) меняет знак. При этом с ростом времени точка, изображающая ΔE'q на плоскости (ΔE'q, ΔΘ), движется по-прежнему по часовой стрелке, так как по-
ток ротора запаздывает в своем изменении по отношению к причине, его вызвавшей.
- Мгновенное изменение мощности при колебаниях угла около среднего положения Θ изобразится снова кривой, получаемой наложением на кривую Рг (Θ) добавочной составляющей. Соответствующая кривая показана на рис. 2.6. При изменении угла изображающая точка по-прежнему вращается по часовой стрелке.
При обходе кривой abcda по указанному направлению при принудительно заданном законе изменения угла в контур регулирования вносится добавочная энергия. В результате система будет неустойчивой, т. е. раз возникшие колебания под действием избыточной энергии будут расходиться в линейной постановке задачи до бесконечности. Имеющиеся в реальной системе ограничения выходного напряжения элементов системы возбуждения приведут к установлению колебательного режима с изменением напряжения ротора от
+ Uf ном до – Uf ном. Устойчивость при углах Θ > Θa, может быть обеспечена снижением коэффициента усиления до значения
К0u = К0u max, при котором величина
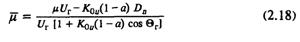
из уравнения (2.11) обратится в ноль (граница устойчивости) или станет положительной (положительное демпфирование). Граница устойчивости при Θ > Θa с учетом того, что знаменатель в (2.18 ) в ноль никогда не обращается, обеспечивается при равенстве нулю числителя. Значит, К0u max≤ μUг[(1-a)Dn], что полностью совпа-
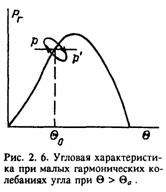 дает с полученным ранее путем приравнивания нулю n-1-го определителя характеристического уравнения (2.6).
дает с полученным ранее путем приравнивания нулю n-1-го определителя характеристического уравнения (2.6).
Нетрудно заметить, что при сниженных значениях коэффициента усиления амплитуда колебаний потока ротора Ā в области режимов
0 ≤ Θ ≤ Θa (рис. 2.5), характеризующая интенсивность демпфирования малых колебаний, возрастает приближаясь к естественной характеристике нерегулируемой машины.
Таким образом, граница колебательной устойчивости может быть получена решением алгебраического уравнения, в которое входят только параметры генератора, Хвн и данные о режиме, а ее асимптота Θ│K0u=∞ определяется приравниванием нулю знаменателя выражения (2.6) аналогично тому, как определяется предел апериодической устойчивости — приравниванием нулю n-го члена характеристического уравнения. Показано также, что снижение коэффициента усиления по напряжению повышает интенсивность демпфирования малых колебаний.
Асимптоту активной мощности Рa, соответствующую асимптоте Θa, определим, выразив на основании уравнений установившегося режима Eq через напряжения на концах передачи и полный угол
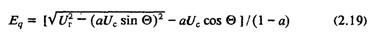
и преобразовав с учетом (2.9) и (2.19) уравнение активной мощности
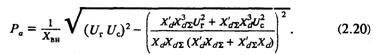
Найдя величину Рa, при определенном экспериментально или при нескольких расчетных значениях Хвн и сравнив ее с номинальной мощностью генератора, проектировщик или наладчик сразу может решить, допустима ли работа данной машины в системе с пропорциональным регулятором напряжения или необходимо сильное регулирование.
2.2.2. Предельно достижимый режим
Как видно из рис. 2.1, устойчивая работа при углах Θ > Θa обеспечивается вплоть до предельного режима Θm, (точка В, в которой K0u min = K0u max ) только при снижении коэффициента уси-
3 ,
ления по напряжению. Соответствующее Θm, значение мощности Рm, является предельной мощностью, которую можно передать при данном законе регулирования возбуждения. Именно стремление обеспечить больший запас устойчивости при упрощении закона регулирования определило снижение К0u резервного регулятора ПДУ систем возбуждения выпуска 70—80-х годов [36 ].
Значения Θm и Рm, могут быть достаточно просто определены еще на стадии проектирования синхронного генератора или станции. Приравняв друг другу (2.5) и (2.6), получим условие
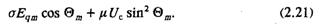
Выразив из него Еq и приравняв его (2.19), после ряда преобразований можно получить биквадратное уравнение относительно sinΘm, требуемое решение которого имеет вид:
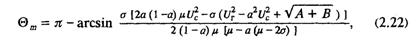
где
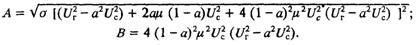
После определения Θm можно найти из (2.19) соответствующее значение Еqm, после чего не составляет труда найти предельное значение активной мощности и из (2.5) или (2.6) величину K0u, при которой оно может быть достигнуто. Например, для расчетного случая при Uг = Uc = 1 эти величины составляют: Θm = 111.2 °, Еqm, = 6.75 е. в.х. х., Рm, = 2.19, К0u = 5 е. в.х. х./е. н.=>1.6 е. в.н./е. н. Таким образом, снижение К0u, позволяет полностью снять вопрос статической устойчивости при любой мощности станции, вплоть до номинальной. Естественно, что при этом интенсивность демпфирования колебаний будет невысока. В дальнейшем мы рассмотрим, каким образом можно удовлетворить оба эти требования.
2.3. Влияние параметров стабилизации на предельный коэффициент усиления по напряжению
Выражения для К0u min и К0u max при идеальном регуляторе позволяют оценить, как скажется введение того или иного параметра стабилизации, применяемого в АРВ—СД, на границах устойчивости. Минимальный коэффициент усиления, определяющий сползание, от них не зависит, а на максимальный коэффициент они действуют по-разному,
Производная напряжения. Коэффициент усиления К1u входит только в числитель выражения (2.6), поэтому введение этого
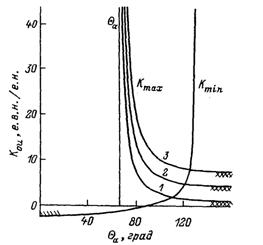
Рис.Предельные коэффициенты усиления при регулировании по отклонению и производной напряжения.
сигнала никак не сказывается на асимптотических значениях угла и мощности, Θa и Рa. Оно несколько поднимает границу колебательной устойчивости и увеличивает реально достижимые значения Θm и Рm (рис. 2.7). Такое смещение границы колебательной устойчивости явно недостаточно.
Производная тока возбуждения. При безынерционном канале производной тока ротора коэффициент К1if входит только в знамена, причем со знаком «+». Следовательно, идеальный сигнал I'f будет уменьшать асимптотические значения угла и мощности и предельные значения К1if. Иными словами, он будет ухудшать условия колебательной устойчивости. На практике это было замечено давно. Было также установлено, что при наличии запаздывания в канале I'f он существенно повышает колебательную устойчивость, особенно в режимах потребления реактивной мощности. Этот случай подробно рассмотрен в гл. 3, а здесь отметим только нецелесообразность увеличения быстродействия по каналу производной тока возбуждения.
Отклонение и первая производная частоты напряжения. Совместное действие этих каналов учитывается в уравнении регулирования (1.19) сигналом идеального отклонения частоты Δfu с расчетным коэффициентом kf, который входит в числисо знаком «+», а в знаменатель — со знаком «-». В результате знаменатель позже переходит в область D> 0 и граница колебательной устойчивости может быть поднята вверх и сдвинута вправо (рис. 2.8). Каждому значению угла Θ > Θa может быть поставлено
3*
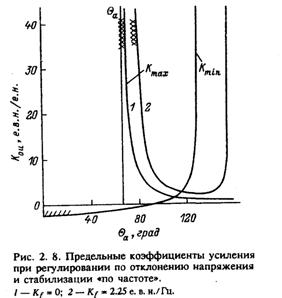
в соответствие значение Кfi, при котором стабилизация «по частоте» обеспечивает смещение асимптот K0u max(P) до P=Pi и K0u max(Θ) — до Θi. Величина Кfi, определяется обращением в ноль знаменателя
(2.6):
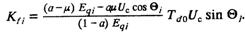
После подстановки значения Еqi, из (2.19) можно получить зависимость Кfi(Θ) в явном виде:
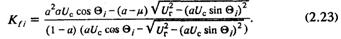
Соответственно смещается вправо асимптота зависимости K0u max(Θ) и теоретически (при безынерционных элементах системы возбуждения) снимается ограничение на его величину.
Аналогично можно при фиксированных значениях коэффициентов в уравнении регулирования (1.19) определить значение Кf, гарантирующее, что граница колебательной устойчивости при определенном угле (или мощности) проходит через точку с заданной величиной К0u:
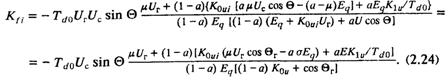
Таким образом, для любого установившегося режима можно найти настройку по каналам стабилизации К0f, К1f, способную обеспечить требуемый запас устойчивости по К0u.
2.4. Влияние реактивных сопротивлений генератора на статическую устойчивость
Положение границы колебательной устойчивости турбогенератора (2.6) во всех режимах определяется тремя параметрами:
Хd, Х'd и Хвн. Опыт показывает, что Хвн — долгоживущий параметр, значения которого обычно лежат в диапазоне 0.2—0.5 о. е. Следовательно, есть возможность проанализировать влияние на устойчивость синхронной и переходной реактивностей, определяющих мас-согабаритные показатели машины, а значит и ее стоимость.
В табл. 2.1 приведены значения Хd и Х'd турбогенераторов мощностью 300—1200 МВт, причем машины расположены в порядке возрастания расчетного параметра b = X'd/Xd. Видно, что во всех случаях 0.132<b<0.16. Для большей полноты таблица дополнена двумя гипотетическими машинами — с уменьшенным (Х'd = 0.3, b = 0.117) и
увеличенным (Х'd= 0.5 , b = 0.213) значениями переходной реактивности.
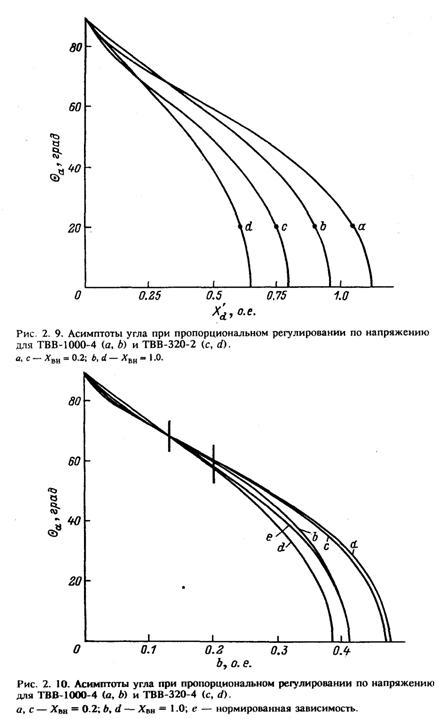
Поскольку взаимное расположение Θa и Θ|P ном не зависит от уровней напряжения, анализ влияния на статическую устойчивость параметров генератора проведем при единичных напряжениях на концах электропередачи. Из таблицы видно, что при выбранном значении Хвн для всех мощных турбогенераторов существует опасность самораскачивания. Значит, все они не могут работать с пропорцио-
Таблица 2.1 Реактивные сопротивления и характерные значения угловдля машин разных типов | |||||
Тип машины | b | Xd | X'd | Θa | Θ | P ном |
— | о. е. | о. е. | град | град | |
Гипотетическая 1 | 0.117 | 2.56 | 0.30 | 70.0 | 72.7 |
ТЗВ-800 | 0.132 | 2.29 | 0.303 | 68.3 | 70.4 |
ТВВ-1000-2 | 0.135 | 2.82 | 0.382 | 67.8 | 74.5 |
ТГВ-300 | 0.137 | 2.135 | 0.30 | 67.8 | 67.9 |
ТГВ-500-2 | 0.139 | 2.56 | 0.355 | 67.4 | 71.2 |
ТВВ-320-2 | 0.152 | 1.698 | 0.258 | 66.1 | 61.9 |
ТВВ-1200-2 | 0.160 | 2.24 | 0.358 | 65.0 | 70.0 |
ТВВ-1000-4 | 0.192 | 2.35 | 0.452 | 61.35 | 71.0 |
Гипотетическая 2 | 0.213 | 2.35 | 0.50 | 58.9 | |
Примечание. Значения Θa и Θ | P ном определены при Uг = Uc= 1, Хвн = 0.2. |

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 |



