Для конических проекций формулы преобразования геодезических координат ( Ө , φ ) в прямоугольные (x, y) координаты имеют вид
x= xp + rsinβ, y =yc + r cosβ,
r = ( Өmin - Ө)/(90 - Ө min) yp + xpctga,
b = a (j - jc )/(j -jmin),
где xp - расстояние от левого края карты до центрального меридиана, yp - расстояние от точки пересечения центральным меридианом нижнего края карты до полюса, yc - расстояние от точки пересечения центральным меридианом нижнего края карты до центра концентрических окружностей, изображающих параллели, α - угол отклонения от вертикали меридиана, проходящего через левый нижний угол карты, φc - геодезическая долгота центрального меридиана, φmin - долгота меридиана, проходящего через левый нижний угол карты, Өmin - геодезическая широта в точке пересечения центральным меридианом нижнего края карты. Картографический смысл этих и других, зависимых от них, параметров конической проекции поясняет рис. 3.2, В.
Конические проекции особо пригодны для территорий, вытянутых вдоль параллелей в целях уменьшения уклонений масштабов от единицы.
Для карт России обычно выбирают конические проекции, в которых воображаемый конус сечет земной шар по параллелям 47° и 62° С. Ш. – это линии нулевых искажений. Вблизи этих линий искажения невелики.
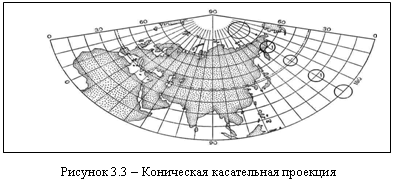 |
Такое представление удобно, поскольку между указанными параллелями размещаются основные хозяйственные зоны нашей страны и здесь сосредоточена максимальная нагрузка карт. Зато в конических проекциях сильно искажены районы, лежащие в высоких широтах, и акватории Северного Ледовитого океана.
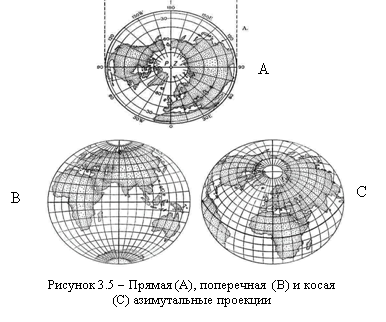
Б) Азимутальные проекции
В прямых азимутальных проекциях (рис. 3.4, А) параллели (альмукантараты) изображаются концентрическими окружностями, меридианы (вертикалы) – пучком прямых, исходящих из центра. Углы между меридианами проекции равны соответствующим разностям долгот.
Промежутки между параллелями определяются принятым характером изображения (равноугольным или др.) или способом проектирования точек земной поверхности на картинную плоскость. Нормальная сетка азимутальных проекций ортогональна.
Азимутальные проекции можно рассматривать как частный случай конических проекций, в которых r1(180°).
Азимутальные проекции применяются как прямые, так и косые и поперечные, что определяется широтой центральной точки проекции, выбор которой зависит от расположения исследуемой территории. Меридианы и параллели в косых и поперечных проекциях (рис. 3.5, В, С) изображаются кривыми линиями, за исключением среднего меридиана, на котором находится центральная точка проекции. В поперечных проекциях прямой изображается также экватор: он является второй осью симметрии.
 |
В проекции масштаб длин может сохраняться в точке или вдоль одной из параллелей (вдоль альмукантарата). В первом случае предполагается касательная картинная плоскость, во втором – секущая. В прямых проекциях формулы даются для поверхности эллипсоида или шара (в зависимости от масштаба карт), в косых и поперечных – только для поверхности шара.
В) Цилиндрические проекции
Цилиндрическая проекция – это проектирование земной поверхности на боковую поверхность цилиндра, которая затем разворачивается в плоскость. Цилиндр может быть касательным к земному шару или секущим его. В первом случае длины сохраняются по экватору. Во втором – по двум стандартным параллелям. На основе цилиндрической проекции составляются космические и аэронавигационные карты.
Цилиндрические проекции бывают прямые, косые и поперечные. В прямых цилиндрических проекциях одни и те же участки поверхности изображаются одинаково вдоль линии разреза в восточной и западной частях карты, что обеспечивает удобство чтения карты по широтным поясам.
Косые цилиндрические проекции имеют географическую сетку, которая дает представление о сферичности земного шара. С уменьшением широты полюса кривизна параллелей увеличивается, а их протяженность уменьшается, что дает представление о сферичности земли.
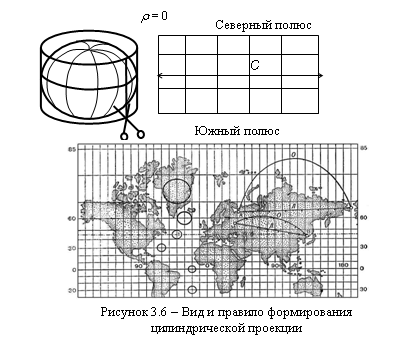 |
В прямых цилиндрических проекциях параллели и меридианы изображаются двумя семействами параллельных прямых линий, перпендикулярных друг к другу. Промежутки между параллелями пропорциональны разностям долгот, промежутки между меридианами определяются принятым характером изображения (равноугольным или др.) или способом проектирования точек земной поверхности на боковую поверхность цилиндра. Из определения проекций следует, что сетка меридианов и параллелей ортогональна. Цилиндрические проекции можно рассматривать как частный случай конических проекций при r0 (вершина конуса в бесконечности).
Прямые цилиндрические проекции, косые или поперечные применяются в зависимости от расположения изображаемой области. В косых и поперечных проекциях меридианы и параллели изображаются различными кривыми, но средний меридиан проекции, на котором располагается полюс косой системы, всегда прямой. В поперечных проекциях, кроме того, прямой линией изображается экватор.
Для карт мира чаще всего применяют цилиндрические проекции, обладающие наименьшими искажениями в области экватора и средних широт. Искажения в прямых цилиндрических проекциях зависят только от широты. В цилиндрических проекциях имеется одна постоянная c, определяющая промежутки между меридианами. Таким образом, геометрический смысл постоянной «c» – это радиус параллели, сохраняющей длины, т. е. стандартной параллели. Ординаты и масштабы длин по параллелям зависят лишь от выбранной широты.
Масштаб длин по параллелям имеет минимальное значение на экваторе, равен единицы на стандартных параллелях и затем, возрастая с увеличением широты, достигает бесконечно большой величины на полюсе.
Если изображаемая область имеет небольшое протяжение по широте и располагается примерно симметрично относительно экватора, целесообразно брать проекцию, сохраняющую длины на экваторе, т. е. такую, чтобы масштаб на экваторе равнялся единице.
Широты стандартных параллелей при одинаковой значимости северной и южной частей изображаемой области могут находиться по следующему условию: масштабы на крайних параллелях, расположенных симметрично относительно экватора, должны быть равны между собой и быть на столько больше единицы, на сколько меньше единицы масштаб на экваторе (секущий цилиндр). Прямые цилиндрические проекции с двумя стандартными параллелями (секущий цилиндр) могут применяться и тогда, когда изображаемая область находится по одну сторону от экватора. Широта стандартной параллели может выбираться примерно посередине изображаемой территории.
Цилиндрические проекции могут находить самое разнообразное применение: от карт мелких масштабов до крупномасштабных, от общегеографических карт до специальных. Проекция Меркатора (частный случай цилиндрической проекции) широко применяется в навигации из-за удобства учета искажений длин. Используется она как для карт отдельных водных бассейнов, так и для изображения мирового океана.
По закономерностям в распределении искажений цилиндрические проекции более всего подходят для изображения сравнительно узкой полосы, так как изоколы[9] изображаются прямыми параллельными линиями, которые могут быть ориентированы так, чтобы располагались по линии наибольшего протяжения изображаемой области. Эта полоса должна быть расположена симметрично относительно экватора – географического или условного, так как искажения изменяются медленно лишь около экватора. Аэронавигационные маршрутные полетные карты чаще всего составляются в косых и поперечных цилиндрических равноугольных проекциях (на шаре).
Для обеспечения обзорности изображения всей земной поверхности или значительных ее частей нередко, несмотря на большие искажения, используют прямые цилиндрические проекции. В этих проекциях одинаково изображаются одни и те же участки земной поверхности вдоль линии разреза – по восточной и западной рамкам карты (дублируемые участки карты) и обеспечивается удобство чтения по широтным поясам (например, на картах растительности, осадков) или по меридианальным зонам (например, на картах часовых поясов).
Косые цилиндрические проекции при широте полюса косой системы, близкой к полярным широтам, имеют географическую сетку, дающую представление о сферичности земного шара. С уменьшением широты полюса кривизна параллелей увеличивается, а протяжение их уменьшается, поэтому уменьшаются искажения и эффект сферичности. В прямых проекциях полюс изображается прямой линией, по длине равной экватору, но в некоторых из них (Меркатора, Уэтча) полюс изобразить невозможно. Полюс изображается точкой в косых и поперечных проекциях. При ширине полосы до 4.5 можно брать касательный цилиндр, при увеличении же ширины полосы следует применять секущий цилиндр и вводить редукционный коэффициент.
Г) Поликонические проекции
При получении поликонической проекции проецирование осуществляется для каждой параллели на свой конус. Представим себе конус, который касается глобуса по северной 50-ой параллели. Перенесем все точки глобуса на эту параллель, затем берем конус, который будет касаться глобуса по 51-ой параллели, и тоже переносим все точки этой параллели на конус. Повторяем операции для 52-ой и так далее. Все конусы будут разные. Чем южнее параллель, тем конус будет более острый. Затем выбирается один из меридианов, например, 90-ый восточной долготы, проходящий примерно по Енисею. То место, где этот меридиан будет пересекать параллель, по которой конус касается глобуса, отмечается особой точкой. Аналогично отмечается точка, где будет пересекаться параллель с меридианом 90 градусов западной долготы.
Затем все полученные конусы разрезаются вдоль так, чтобы точка реза проходила через точку 90 градусов западной долготы, разворачиваются на плоскости (на столе) и мы видим, что на каждом из них нарисована узкая полоска картографического изображения, соответствующая той параллели, в которой наш конус касался глобуса. После этого вырезаются эти узкие полоски, которые будут представлять собой дуги, и складываются на столе так, чтобы они касались друг.
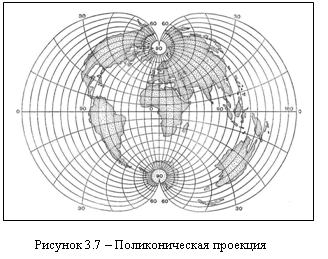
Для каждого конкретного задания выбирают ту или иную зависимость полярных координат от широты до долготы.
Д) Видоизмененная простая поликоническая проекция
В 1913 г. на Mеждународной конференции в Париже были приняты «Основные положения по созданию Международной миллионной карты мира». Карту было предложено создать на основе видоизмененной простой поликонической проекции с учетом особенностей ее применения для создания масштаба 1:1
Земная поверхность, принимаемая за поверхность эллип-соида вращения, делится линиями меридианов и параллелей на трапеции. Трапеции изображаются на отдельных листах в одной и той же проекции (для масштаба 1:1 в видоизмененной простой поликонической). Листы Международной карты мира масштаба 1:1 имеют определенные размеры сторон трапеций – по меридианам 4, по параллелям 6; на широте от 60 до 76 листы сдваивают, они имеют размеры по параллелям 12; выше 76 листы счетверяют, их протяжение по параллелям 24. Номенклатура сдвоенных и счетверенных листов карты складывается из обозначений широтного пояса и соответственно двух или четырех колонн, например Р 39,40. Особенности видоизмененной простой поликонической проекции и распределение искажений в пределах отдельных листов карты масштаба 1:1 000 000 следующие. Меридианы изображаются прямыми линиями. Длина двух меридианов, отстоящих от среднего на 2 по долготе (на 4 на сдвоенных листах и на 8 – на счетверенных), искажений не имеет. Крайние параллели каждого листа (северная и южная) являются дугами окружностей, центры этих параллелей находятся на среднем меридиане, длина их не искажается.
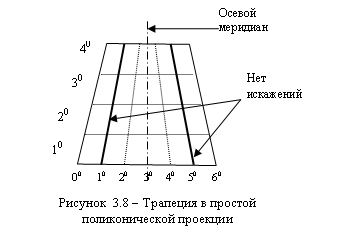 |
Картографическая сетка строится через 1 по широте и по долготе, на сдвоенных листах по долготе через 2, на счетверенных – через 4. Таким образом, все листы карты масштаба 1:1 имеют пять параллелей и семь меридианов. Криволинейные меридианы простой поликонической проекции заменяются в видоизмененной поликонической проекции прямыми, соединяющими соответственные точки крайних параллелей, поэтому масштабы на внутренних параллелях будут меньше единицы. Минимальный масштаб получим на средней параллели каждого листа карты.
Достоинством видоизмененной простой поликонической проекции является небольшая величина искажений. Анализ в пределах листа карты показал, что искажения длин не превышают 0,10, площади 0,15, углов 5 и являются визуально практически неощутимыми. Недостатком этой проекции считают появление разрывов при соединении листов по меридианам и параллелям.
 |
Е) Псевдоцилиндрические проекции
Параллели в этих проекциях изображаются в виде параллельных линий, меридианы – в виде кривых (дуг, синусоид, гипербол, парабол или эллипсов.), симметричных относительно среднего прямолинейного меридиана. Полюс изображается точкой или полярной линией. Длина линии устанавливается или получается из задания. Сетка не совпадает с направлением меридианов и параллелей, за исключением среднего меридиана и экватора. Псевдоцилиндрическая проекция используется при изображении всей поверхности или ее большей части в мелких масштабах.
Ж) Проекция Гаусса-Крюгера
В 1825 г. К. Гаусс впервые решил задачу по изображению одной поверхности на другой с сохранением подобия в бесконечно малых частях. Частным случаем этой задачи является отображение поверхности эллипсоида вращения на плоскости. В 1912 г. А. Крюгер вывел и опубликовал рабочие формулы этой поверхности. После этого проекция получила название Гаусса-Крюгера и нашла широкое применение в топографо-геодези-ческих работах.
В проекции Гаусса-Крюгера поверхность эллипсоида на плоскости отображается в виде совокупности меридианных зон, ширина которых равна 6 (для карт масштабов 1:– 1:10 000) и 3 (для карт масштабов 1:5 000 –1:2 000). Меридианы и параллели изображаются кривыми, симметричными относительно осевого меридиана зоны и экватора, однако их кривизна настолько мала, что западная и восточная рамки карты изображаются прямыми линиями. Параллели, совпадающие с северной и южной рамками карт, изображаются прямыми на картах крупных масштабов (1:2 000–1:50 000), на картах мелких масштабов они изображаются кривыми. Начало прямоугольных координат каждой зоны находится в точке пересечения осевого меридиана зоны с экватором.

Территорию бывшего СССР, например, покрывают 29 шестиградусных зон с номерами от 4 по 32. Изоколы в проекции Гаусса-Крюгера имеют вид овалов, вытянутых вдоль осевого меридиана; в пределах отдельных листов карт они имеют вид прямых. Максимальные искажения в каждой зоне будут при значениях широт 0 и ±3, в этих точках они достигают 0,14. На расстоянии около 200 км по обе стороны от осевого меридиана и параллельно ему находятся две изоколы с нулевыми искажениями длин. При дальнейшем удалении от осевого меридиана масштаб длин становится больше единицы и достигает максимума на пересечении крайних меридианов зоны с экватором (+0,05) .
Осевые меридианы трехградусных зон совпадают попеременно то с осевыми меридианами шестиградусных зон, то с крайними меридианами этих зон.
Номер зоны N и долгота осевого меридиана L0 в градусах связаны между собой равенством L0 = 6N – 3.
Чтобы исключить из обращения отрицательные ординаты и облегчить пользование прямоугольными координатами на топографических картах, ко всем координатам y добавляют постоянное число метров). Точка пересечения осевого меридиана и экватора (начало координат) имеет значения: X = 0 км; Y = 500 км.
Чтобы знать, к какой зоне относятся координаты, необходимо к значению y слева приписать номер зоны. Например, запись координаты y =30 м означает, что точка находится в 30-й зоне, ее реальная координата равна м. Территория РСФСР находится в Северном полушарии, следовательно, все координаты Х – положительные. Координаты y будут отрицательными, если точка находится левее осевого меридиана, и положительными, если правее.
3.3 Преобразования цифровых карт в ГИС
Функции преобразования плоскости предназначены для аналитического трансформирования изображения с использованием математического преобразования плоскости по набору опорных точек (тиков). Опорные точки выбираются исходя из особенностей изображения (узловые точки, сетки, узлы пересечения параллелей и меридианов, углы рамки, характерные точки контура и т. п.).
Для осуществления геометрического преобразования определяются две системы координат:
- первая система координат связана с исходным изображением (до преобразования), обозначим координаты некоторой точки в этой системе ![]()
![]() ;
;
- вторая система связана с трансформированным изображением (после преобразования), обозначим координаты точки в этой системе ![]() .
.
После задания соответствующих опорных точек в первой и второй системах координат (ТИКов) определяется закон преобразования, по которому и происходит преобразование координат всех точек и в конце – всей цифровой карты.
1. Преобразование подобия характеризуется тем, что все фигуры на плоскости переводятся в геометрически подобные им фигуры. Все углы между пересекающимися прямыми сохраняют свои значения, а все линейные размеры увеличиваются или уменьшаются в одинаковое число раз. Практически преобразование подобия решает задачу перехода от одной декартовой системы координат к другой. Чтобы задать преобразование, достаточно выбрать в качестве опорных точек любые две точки плоскости и указать старые и новые координаты этих точек. Удобно принять в качестве опорных точек начало координат и какую-либо точку, лежащую на оси X или Y.
2. Аффинное преобразование, которое называют также линейным преобразованием. Это преобразование, которое всегда переводит прямые линии в прямые, при этом параллельные прямые остаются параллельными. Углы между пересекающимися прямыми могут изменяться или оставаться прежними. Рассмотренное выше преобразование подобия является частным случаем аффинного преобразования. Можно сказать также, что произвольное аффинное преобразование переводит заданный квадрат в любой заданный параллелограмм, в то время как преобразование подобия переводит квадрат в любой другой заданный квадрат. Чтобы задать аффинное преобразование, достаточно выбрать в качестве опорных точек три любые точки, не лежащие на одной прямой, и указать старые и новые координаты этих точек. Удобно принять в качестве опорных точек начало координат и две точки, лежащие соответственно на осях X и Y. Данный тип преобразования не может обеспечить точность преобразования опорных точек, но зато сохраняет все прямые линии прямыми.
3. Полиномиальное преобразование. Это один из типов нелинейных преобразований, т. е. таких, которые гарантируют точное преобразование для любого количества опорных точек, расплачиваясь за это искривлением прямых линий. Как известно из математического анализа, если заданы значения некоторой функции вещественного или комплексного переменного в N различных точках, то можно единственным образом построить полином степени N–1, принимающий в этих точках заданные значения (интерполяционный полином Лагранжа). Именно таким образом строится закон преобразования координат для полиномиального типа преобразования. Точки плоскости рассматриваются как комплексные числа. Для любого количества опорных точек гарантируется точное (в пределах погрешности вычислений) преобразование их координат в заданные новые значения. Интересной особенностью этого преобразования является то, что, несмотря на искривление линий, все углы пересечения линий сохраняют неизменное значение.
К сожалению, полиномиальное преобразование как средство решения задачи уточнения координат имеет ряд недостатков, основной из которых - чрезмерное искривление линий, резко усиливающееся по мере удаления от опорных точек.
4. Локальное преобразование. В отличие от полимиального типа преобразования, данное преобразование основано не на строгих математических предпосылках, а скорее на соображениях здравого смысла. Идея заключается в следующем. Для каждой из опорных точек можно тем или иным способом построить такую нелинейную функцию, которая преобразует старые координаты этой точки в ее новые координаты, а для остальных точек изменяет координаты тем менее, чем дальше точка отстоит от опорной. На большом расстоянии от опорной точки изменение координат должно стремиться к нулю. Построив подобные функции для каждой опорной точки, можно определить общее преобразование как взвешенную сумму этих функций, при этом коэффициенты суммирования нетрудно рассчитать таким образом, чтобы компенсировать небольшой сдвиг каждой опорной точки под влиянием перемещения остальных опорных точек.
5. Комбинированные аффинно-нелинейные преобразования. Можно ожидать заметного улучшения качества трансформации, если сначала выполнить аффинное преобразование по методу наименьших квадратов, а затем применить один из нелинейных методов. При этом на первом (аффинном) этапе в большинстве случаев удается значительно сократить расстояния, на которые должны быть перемещены опорные точки, и в результате этого второй (нелинейный) этап преобразования вносит значительно меньшие нелинейные искажения, чем при непосредственном применении без предварительного выполнения линейной части преобразования.
Преобразования подобия
Постановка задачи. В системе координат XOY имеем точку О с координатами (Xс, Yс). Новая система координат получена путем сдвига начала координат ![]() относительно начала первой системы координат, поворота осей на угол a (рис. 3.12).
относительно начала первой системы координат, поворота осей на угол a (рис. 3.12).
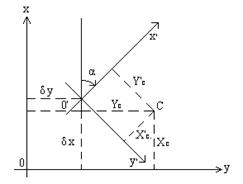
Рисунок 3.12 – Преобразования подобия
Обозначим ![]() – координаты точки в старой и новой системах координат соответственно.
– координаты точки в старой и новой системах координат соответственно.
Переход из XOY в X'O'Y' выполняется по формулам :
![]()
Для обратного перехода используются формулы:
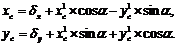
Если известен коэффициент масштабирования по осям (kx и ky ), то формулы преобразования примут вид:
![]()
Использование преобразования позволяет восстанавливать изображение, претерпевшее такие изменения, как сдвиг, поворот, масштабирование.
Аффинное преобразование
Формулы аффинного преобразования:
![]()
где 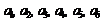 – искомые коэффициенты,
– искомые коэффициенты, 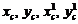 – координаты точки в старой и новой системах координат соответственно.
– координаты точки в старой и новой системах координат соответственно.
Коэффициенты преобразования могут быть вычислены по 3-м точкам, не лежащим на одной прямой, координаты которых заданы до и после преобразования. Коэффициенты преобразования могут быть также определены из условия минимизации отклонения образов m заданных точек от некоторых фиксированных m точек (m>3).
Использование аффинных преобразований позволяет восстанавливать изображение, претерпевшее такие изменения, как сдвиг, поворот, масштабирование (в том числе с различными коэффициентами по осям X и Y) по 3-м опорным точкам, а также с помощью m опорных точек несколько уменьшать отклонения точек изображения, не подчиняющиеся простому закону (например, с неравномерным растяжением (сжатием) бумаги). Аффинное преобразование прямые переводит в прямые. Это позволяет использовать аффинное преобразование области изображения, разбитой на треугольники, с сохранением непрерывности на границах треугольников.
Проективное преобразование
Формулы проективного преобразования:
![]()
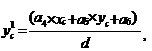
![]()
Коэффициенты преобразования могут быть вычислены по 4-м точкам (никакие 3 из которых не лежат на одной прямой), координаты которых заданы до и после преобразования. Проективное преобразование позволяет совмещать изображение по 4-м опорным точкам, что удобно, например, при цифровании расчлененных оригиналов карт (по традиционной ручной технологии расчлененные оригиналы совмещаются по 4-м крестам) или при раздельном цифровании слоев изображения. Проективное преобразование прямые переводит в прямые, что позволяет использовать проективное преобразование области изображения, разбитой на четырехугольники, без сохранения непрерывности на границах четырехугольников.
Квадратичное преобразование
Формулы преобразования с помощью полиномов второй степени:
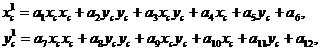
где![]() – коэффициенты преобразования;
– коэффициенты преобразования;
![]() – координаты точки в исходной и результирующей системах координат соответственно.
– координаты точки в исходной и результирующей системах координат соответственно.
Коэффициенты преобразования могут быть вычислены по 6-ти точкам, координаты которых заданы до и после преобразования. Коэффициенты преобразования могут быть также определены из условия минимизации отклонения образов m заданных точек от некоторых фиксированных m точек (m>6).
Преобразование с помощью полиномов второй степени позволяет совмещать изображение по 6-ти опорным точкам непрерывно и не сохраняет прямые линии.
Преобразование полиномами 5-й степени
Формулы преобразования с помощью полиномов пятой степени:
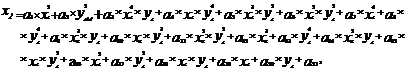
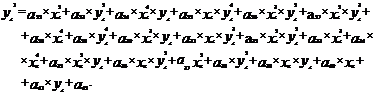
Коэффициенты преобразования могут быть вычислены минимум по 21-й опорной точке, координаты которых заданы до и после преобразования. Коэффициенты преобразования могут быть также определены из условия минимизации отклонения образов m заданных точек от некоторых фиксированных m точек ( m>21 ).
Преобразование с помощью полиномов пятой степени целесообразно использовать при наличии большого числа опорных точек (по крайней мере 60–70), если ни аффинное, ни квадратичное преобразования не дают желаемого результата. Следует также помнить, что несколько «плохо» выбранных опорных точек могут существенно влиять на результат.
Вопросы к теме 3
1. Для каких целей служит дигитайзер?
2. Какие проблемы нужно решать при автоматической векторизации?
3. Для чего при векторизации используется маска?
4. Что такое «рабочая область» в процедуре векторизации?
5. Как осуществляется процедура фильтрации?
6. Когда нужно использовать проекционные преобразования?
7. Какие проекции чаще всего используются в ГИС?
8. Чем отличается равноугольная проекция от равновеликой?
9. Как определяются постоянные величины конической проекции?
10. Что такое секущая параллель?
11. Может ли стандартная касательная параллель пройти по экватору?
12. Когда целесообразно использовать коническую проекцию с одной стандартной параллелью?
13. Чем отличаются прямая коническая проекция от поперечной конической проекции?
14. Каков принцип построения азимутальной проекции?
15. Как выглядят параллели и меридианы в прямых азимутальных проекциях?
16. Как выглядят параллели и меридианы в прямых цилиндрических проекциях?
17. В каких случаях целесообразно использовать цилиндрические проекции?
18. Как изображается полюс в прямых цилиндрических проекциях?
19. Чем отличаются поликонические проекции от конических?
20. Почему трапеции для широт выше 76 0 счетверяют?
21. Скольким градусам по параллелям соответствуют самые северные трапеции?
22. В какой части трапеции наблюдается максимальное искажение?
23. Что такое изокола?
24. В чем проявляется недостаток видоизмененной простой поликонической проекции?
25. В какой проекции изоколы имеют вид овалов?
Тема 4. Инструментальные средства ГИС
4.1 Обзор промышленных пакетов ГИС
Продукция компании ESRI. Самая крупная в мире и самая известная компания по производству ГИС-продукции – это Институт исследования окружающей среды (ESRI) в Калифорнии (США). Она работает на рынке более 30 лет и имеет в настоящее время более пользователей в мире. Компания создала и сопровождает лидирующий пакет ГИС ESRI.
В России компания ESRI более 10 лет имеет собственного дистрибьютора ДАТА+ и насчитывает около 1000 пользователей своего программного продукта. Компания предлагает большую палитру поддержки своего продукта. Одна из немаловажных вещей – это то, что в России имеется центр по подготовке кадров. Продукты ESRI отличает открытость, интеграция и доступность: от простых бесплатных Viewer’ов, простых приложений для бизнес–людей, программных разработок систем настольного картирования к мощным профессиональным ГИС.
Основной и главный продукт ESRI – это профессиональная ГИС, которая называется ArcInfo. Это – основа, на которой развиваются все остальные программные разработки компании. В настоящее время происходят существенные изменения в ArcInfo. Она идет по пути открытости. Первый шаг открытости заключается в переходе ArcInfo с платформы Unix на платформу Windows NT.
Версия 7.1.2. имеет открытую среду разработки, то есть теперь ArcInfo можно настраивать с помощью обычных стандартных средств настройки, таких как Visual Basic, Delphi, Visual C. Стоимость программы более 2000$.
ArcInfo была первой ГИС, использующей векторно-топологическую структуру данных и полностью интегрирующей возможности реляционной базы данных. Поскольку ArcInfo одинаково успешно работает с разнообразным аппаратным обеспечением и периферийными устройствами, пользователи всегда имеют возможность быстро модернизировать свои системы под новые задачи и адаптировать их к самой современной компьютерной технике. Макроязык ArcInfo (AML) открывает доступ ко всем базовым возможностям пакета, позволяет создавать на их основе собственные приложения или использовать приложения, разработанные другими пользователями.
Второй важный продукт ESRI, не менее популярный не только у нас в стране, но и во всем мире, это ArcVeiwer. Он относится к числу настольных ГИС. Эта ГИС осваивается просто и для этого не надо иметь профессиональную подготовку. ArcVeiwer имеет наращиваемые функциональные возможности, ГИС легко «подогнать» под пользователя. ArcVeiwer – хотя и простая, но мощная система. В ней можно работать и с картами, и с таблицами, и со снимками, с текстовой информацией, связывая между собой эти документы.
ArcVeiwer 1 – русская версия. Пакет имеет русский интерфейс, русскую базу данных, русские учебники, русский Help. Архитектура несколько изменена по сравнению с исходной версией. Она имеет базовое ядро и модели расширения. Часть из них поступает с ядром, как обязательный пакет. Часть можно приобрести дополнительно. Стоимость полной программы ArcVeiwer около 1 000$.
Один из важных модулей компании ESRI – это модуль SpecialAnalyst, который позволяет работать с поверхностями, причем в виде поверхности изображается не только привычный нам рельеф, но и поля загрязнения, демографические данные, все то, что имеет непрерывное распространение. Модуль 3DAnalyst позволяет моделировать объекты и явления в привычном трехмерном изображении. Это расширение особенно удобно для градостроителей и архитекторов, которые привыкли видеть город в естественном виде.
Мощное расширение ArcInfo: модуль который разработан бизнес–партнером ESRI фирмой ERDAS – пакет для обработки снимков (аэроснимков, космических снимков и др.). Современное формирование данных без снимков трудно представимо, особенно для динамических структур. Прямо в ArcInfo существуют теперь огромнейшие возможности обработки снимков.
NetAnalyst – программный модуль для анализа сетей. Это могут быть коммуникационные сети, дорожные, транспортные, сети для решения оптимизационных задач, для решения задач по распределению ресурсов, для отслеживания различных коммуникаций.
Новое расширение Dialog Disigner – это средство (можно получить для пользователей ArcVeiwer бесплатно), которое позволяет настроить диалоги, строить красивые диалоговые окна, к каким привыкли пользователи ГИС, используя стандартные среды разработки Visual Basic и т. д.
Модуль Track Analyst позволит моделировать изменение объектов не только в пространстве, но и во времени. Например, с помощью такого модуля можно будет проследить передвижение торнадо во времени и пространстве.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 |



