Геоинформационные системы общий курс (стр. 3 )

Принцип второй. Возможность лаконичного объяснения природы анализируемых многомерных структур. Многомерная структура – это множество статистически обследованных объектов реального мира . Результаты обследования представляются в одной из двух форм:

-  в виде таблицы «объект-свойство» (ТОС), которая имеет вид где 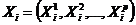– вектор значений анализируемых признаков, зарегистрированных на i-том объекте.

-  матрицы парных сравнений вида объектов вида:

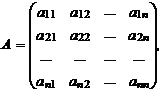
где элемент определяет результат сопоставления объектов и в смысле некоторого заданного отношения: . Отношение может выражать, например, меру сходства или различия элементов и , меру их связи, геометрическое расстояние между объектами, отношение предпочтения (=1, если объект не хуже объекта и = 0 в противном случае) и др.

Под возможностью лаконичного объяснения природы анализируемой многомерной структуры понимается априорное допущение, что существует небольшое (по сравнению с числом признаков ) число типообразующих (определяющих) факторов, с помощью которых могут быть достаточно точно описаны все элементы матриц Х и А, а также характер связей между ними. При этом определяющие факторы могут находиться как среди статистически исследуемых данных, так и среди латентных, т. е. статистически не наблюдаемых, но восстанавливаемых через исходную информацию данных. Пример – периодическая система Менделеева. В ней определяющим фактором (характеристикой) всех элементов-объектов является заряд атомного ядра элемента.

Принцип третий. Максимальное использование «обучения» в настройке математических моделей классификации. Если исследователь располагает «входами» и «выходами» модели классификации, то исходный набор данных называют обучающей выборкой. Целью исследования является описание процедур, с помощью которых для любого элемента, вновь поступившего на вход, можно было бы с достаточной точностью определить номер класса, к которому он относится. Такие задачи – типичные задачи медицинской диагностики, где заранее известны наборы симптомов различных заболеваний, и пациенту, обратившемуся к врачу, после обследования ставится диагноз на основе уже имеющегося опыта.

Однако имеется ряд задач, для которых обучающая выборка полностью неизвестна, например, в больницу поступил больной с симптомами неизвестной врачу болезни. В этом случае по такой обедненной входной информации может быть произведена «настройка» математической модели.

Принцип четвертый. Оптимизационная формулировка задач классификации. Среди множества возможных методов, реализующих поставленную цель классификационной обработки входных данных, нужно найти наилучший метод с помощью оптимизации некоторого заданного критерия (функционала) качества. Как правило, это достигается с учетом априорной информации об объекте исследования.

Содержательная постановка задачи автоматической классификации. Всякие закономерности ищутся для практического удобства. Закономерности «групповой похожести» позволяют сильно сократить описание ТОС при малой потере информации. Вместо перечисления всех объектов исходного множества можно составить список «типовых» или «эталонных» представителей групп, указать номера объектов, попавших в эти группы, и средние или максимальные отличия их свойств от свойств «эталонов». При небольшом числе групп описание расклассифицированных данных становится обозримым и легко интерпретируемым. Такая группировка выполняется с помощью методов таксономии (синонимы: автоматическая классификация, кластерный анализ, самообучение). Алгоритмы автоматической классификации (АК), а их известно более сотни, отличаются друг от друга процедурой группировки (разбиения) и критерием качества. Но во всех алгоритмах используются общие понятия.

Пусть данные ТОС, подлежащие классификации, содержат М объектов O =, описанных свойствами каждый X =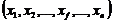. Требуется сформировать К таксонов , каждый из которых описывался бы Т характеристиками S = 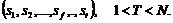Различные варианты разбиения объектов на K таксонов будем сравнивать по критерию качества .

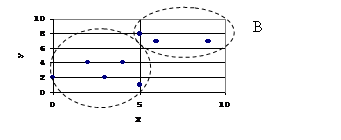
Если свойства представить в виде координат метрического пространства, то каждый объект со своими значениями свойств будет отображаться в некоторую точку этого пространства (рис. 2.1). Два объекта с почти одинаковыми значениями свойств отобразятся в две близкие точки, объекты с сильно различающимися свойствами будут представлены далекими друг от друга точками. Если получатся «сгустки» точек, отделенные от других сгустков промежутками, то их целесообразно выделить в отдельные структурные части множества – классы. Таким образом, можно получить K таксонов (), каждый из которых объединяет точки с «близкими» значениями свойств. В дальнейшем каждый новый объект, описанный набором характеристик , с помощью методов распознавания образов может быть отнесен к тому или иному классу.

Рассмотрим два простейших алгоритма АК, известных как эвристические алгоритмы. Отличительной чертой этих алгоритмов является то, что они выделяют таксоны простой гиперсферической формы. Базовым алгоритмом является алгоритм ФОРЕЛЬ (от первых букв ФОРмальный АЛгоритм).

2.2.2 Эвристический алгоритм «Форель»

Алгоритм ФОРЕЛЬ работает с ТОС, элементами которой являются только количественные данные. Объекты, включенные в один класс, попадают в гиперсферу с центром С и радиусом . Изменяя радиус, можно получить разное количество классов К. При фиксированном заданном радиусе алгоритм ФОРЕЛЬ работает следующим образом.

1. Центр некоторой гиперсферы с радиусом помещается в любую из точек исходного множества объектов.

2. Определяются точки, оказавшиеся внутри этой гиперсферы. Для этого вычисляется расстояние от точки до всех М точек и те из них, для которых , считаются «внутренними».

3. Для внутренних точек вычисляется центр тяжести (точка с координатами, равными усредненным значениям по каждому признаку).

4. Центр сферы перемещается в вычисленный центр тяжести .

5. Для нового центра сферы вновь находятся внутренние точки и их центр тяжести.

6. Процедура перемещения гиперсферы повторяется до тех пор, пока не перестанут изменяться координаты центра тяжести . При этом центр гиперсферы перемещается в область сгущения точек и останавливается в области одного из таких сгустков точек исходного множества А.

7. Точки, попавшие внутрь этой гиперсферы, объявляются классом и из дальнейшего рассмотрения исключаются.

8. Центр гиперсферы совмещается с любой из оставшихся точек. Процедура повторяется до тех пор, пока все исходное множество точек не будет разделено между классами.

Очевидно, что количество классов K тем больше, чем меньше радиус . Желательное количество классов может быть подобрано соответствующим подбором . Для этого рекомендуется последовательно уменьшать радиус от , при котором все точки объединяются в один класс, до тех пор, пока K не будет равен заданному (или наиболее близкому к заданному) числу классов.

Основной недостаток данного алгоритма заключается в том, что в зависимости от того, в какой последовательности эвристически выбирать начальные точки-центры гиперсфер, можно получить разные разбиения исходного множества элементов по классам, отличающиеся как количеством элементов в классах (мощностью класса), так и радиусом гиперсфер . Выбор одного решения из многих делается по критерию качества .

где - квадрат евклидова расстояния от точки с координатами до центра своего класса , а – число объектов в классе (мощность класса) . Лучшему варианту классификации соответствует минимальное значение критерия . Выбор такого критерия обосновывается интуитивными правилами «ручной» группировки. Обычно объединяют в одну группу объекты, мало отличающиеся друг от друга или от «типичного» объекта.

2.2.3 Вариационный алгоритм «Краб»

Семейство алгоритмов КРАБ (КРАтчайший Путь) основано на формировании незамкнутого связного графа и проведении разбиения множества исходных объектов с его помощью. Эти алгоритмы позволяют строить классы произвольной формы и размеров, для чего стремятся реализовать действия, выполняемые человеком при классификации вручную. Чем руководствуется при разбиении человек?

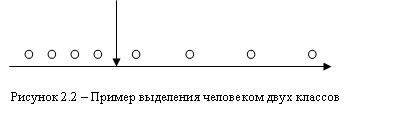
Естественно, человек стремится использовать некоторую форму близости точек и считает, что классификация тем лучше, чем меньше расстояния между точками одного и того же класса. Кроме того, человек увереннее выделяет классы, если сгустки точек дальше удалены друг от друга, так что вводится мера удаленности . При прочих равных условиях человека больше устраивает, когда распределение точек по классам приблизительно равномерно . Чем больше отличие в мощности классов, тем хуже классификация. Психологические эксперименты показали, что человек не всегда объединяет точки в один класс по принципу «ближний к ближнему». Так, для рисунка 2.2 пятая по счету точка ближе к четвертой, но человек проведет границу классов между четвертой и пятой точками. Он обращает внимание на изменения плотности точек . Если подобрать подходящие меры для ,, и , то можно добиться совпадения результатов автоматической и ручной группировки.

Класс 1 Класс 2

Для подбора , , и используют свойства кратчайшего незамкнутого пути (КНП) – связный граф без петель, соединяющий все точки и имеющий минимальную длину ребер (рис. 2.3) .

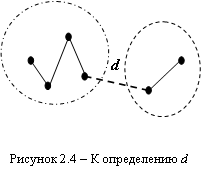
Если разрезать одно ребро (рис. 2.4), то получится два класса, если разрезать (К–1) ребро КНП, мы получим К классов точек.

1. Мерой близости объектов внутри классов считают среднюю длину ребер КНП, соединяющего все точки одного класса:

где – длина j-того ребра КНП, – число объектов в классе .

Общей мерой близости внутренних точек классификации считают величину:

,

т. е. среднюю длину всех внутренних ребер.

2. Расстояние между классами также считают по КНП как среднюю длину ребер, соединяющих классы:

.

3.   Через КНП можно определить и меру локальной неоднородности расстояний между точками . Для этого обозначим длину некоторого ребра , а длину наименьшего примыкающего к нему ребра через . Тогда . Чем меньше величина , тем больше отличие в длинах соседних ребер, тем с большим основанием можно считать, что по ребру пройдет граница.

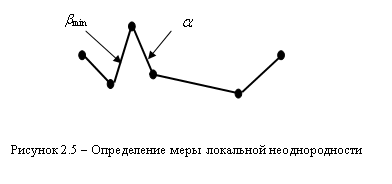
Общая мера неоднородности определяется по формуле:

.

4. Равномерность распределения точек по классам может быть определена монотонной функцией, меняющейся в диапазоне от 0 до 1. Такой функцией может служить выражение:

.

Общий критерий качества в алгоритме КРАБ сформулирован так:

Проверка на двумерных массивах показала, что чем лучше классификация, тем больше значение .

Выделяемые классы могут иметь любую форму.

Алгоритм КРАБ:

1.  Проводится кратчайший незамкнутый путь между всеми точками исходного множества.

2.  Если задано число классов (K), на которое необходимо провести разбиение, то путем перебора выбираются (K–1) ребро, проведение границ по которым даст максимальное значение функционала .

3.  Если исследователю не важна равномерность классов по числу объектов, то используется модификация .

Возникает закономерный вопрос: существует ли объективная автоматическая классификация или всякая классификация субъективна. Все реальные объекты имеют огромное число свойств. Выделение конкретного числа свойств – уже акт субъективный. Меры близости и критерий качества субъективны. Цель, для которой проводится обработка данных, в данном случае классификация, – ставится человеком. Таким образом можно считать, что объективной классификации не существует.

Иногда можно встретиться с ситуацией: программа классификации на реальных данных выдает «плохой» результат, т. е. выделился один большой класс, а остальные данные «рассыпались» по маленьким классам (даже с мощностью равной единице). Но не всегда в этом виноват алгоритм или программа, реализующая его. Например, исходная совокупность может быть описана нормальным законом распределения. Никакая программа не разобьет его на 10 однородных классов.

Результаты классификации зависят и от того, какую значимость мы придаем свойствам объектов. Если свойство в три раза более важно, чем свойство , то в вычислениях это значение нужно использовать в явном виде. Например, при вычислении расстояния между объектами и можно пользоваться следующей мерой:

,

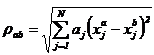где – относительный вес признака, а 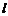принимает разные значения в разной метрике (в евклидовой ).

2.3 Базовые модели данных в ГИС

2.3.1 Инфологическая модель

Инфологическая модель /4/ строится на основе естественного понимания человеком окружающего мира и дает формальное описание предметной области и отображает реальный мир в некоторые понятные человеку концепции, полностью независимые от параметров среды хранения данных. Основными конструктивными элементами инфологических моделей являются сущности (объекты), связи между ними и их свойства (атрибуты).

Сущность – это любой различимый объект (объект, который можно отличить от другого), информацию о котором необходимо хранить в базе данных ГИС. Сущностями могут быть люди, места, самолеты, рейсы, вкус, цвет и т. д. Необходимо различать такие понятия, как тип сущности и экземпляр сущности. Понятие «тип сущности» относится к набору однородных личностей, предметов, событий или идей, выступающих как целое. «Экземпляр сущности» относится к конкретной вещи в наборе. Например, типом сущности может быть ГОРОД, а экземпляром – Москва, Киев и т. д.

Объекты могут быть атомарными и составными.

Атомарный объект – это объект некоторого типа, разложение которого на более мелкие объекты внутри этого типа невозможно, например, в группе людей атомарным объектом будет один человек, дробление которого на более мелкие составные части переведет его в тип – части тела человека.

Составной объект включает в себя некоторое количество более мелких (в том числе и атомарных) объектов, например, студенческая группа состоит из студентов, которые являются атомарными объектами.

Объекты характеризуются свойствами (атрибутами) и взаимосвязью с другими объектами.

Атрибут – поименованная характеристика сущности. Его наименование должно быть уникальным для конкретного типа сущности, но может быть одинаковым для различного типа сущностей (например, атрибут «цвет» может быть определен для многих сущностей: собака, автомобиль, дым и т. д.). Атрибуты используются для определения того, какая информация должна быть собрана о сущности. Примерами атрибутов для сущности «автомобиль» являются «тип», «марка», «цвет» и др. Здесь также существует различие между типом и экземпляром. Тип атрибута «цвет» имеет много экземпляров или значений: красный, синий, белая ночь и т. д.

Свойство может быть не определено явно, а охарактеризовано как утверждение по поводу множества объектов типа, например, можно не описывать некоторый цветок, а отнести его к классу «ромашка», тогда его свойства будут без описания понятны.

Абсолютного различия между типами сущностей и атрибутами нет. Атрибут является таковым только в связи с типом сущности. В другом контексте атрибут может сам выступать как самостоятельная сущность. Например, для автомобильного завода цвет – это только атрибут продукта производства, а для лакокрасочной фабрики цвет – тип сущности.

Взаимосвязь сущностей – это ассоциирование двух или более сущностей. Одно из основных требований к организации базы данных – это обеспечение возможности отыскания одних сущностей по значениям других, для чего необходимо установить между ними определенные связи. А так как в реальных базах данных нередко содержатся сотни или даже тысячи сущностей, то теоретически между ними может быть установлено более миллиона связей. Наличие такого множества связей и определяет сложность инфологических моделей.

Цель инфологического проектирования – формализация объектов реального мира и методов обработки информации в соответствии с поставленными задачами обработки и выдачи информации.

Инфологическая модель носит описательный характер и включает в себя ряд компонентов (рис. 2.6):

1)  описание предметной области;

2)  описание методов обработки;

3)  описание информационных потребностей пользователей.

2.3.2 Логические модели данных

Инфологическая модель должна быть отображена в компьютерно-ориентированную даталогическую модель, «понятную» СУБД. Наиболее близка к концептуальной модели, модель «Сущность-связь».

А) Модель данных ГИС «Сущность-связь»

Теоретической основой ЕR-моделей является модель Петера Пин-Шен Чена (1976), которая послужила в качестве средства концептуального проектирования. В основе представления Чена лежит заключение: предметная область – это совокупности объектов, находящихся друг с другом в различных связях. Моделирование предметной области базируется на использовании графических диаграмм, включающих небольшое число разнородных компонентов.

Сущность (entity) – это «предмет», который может быть идентифицирован некоторым способом, отличающим его от других «предметов». Конкретные человек, компания или событие являются примерами сущности[6]. Для каждой связи характерно число связываемых сущностей. Такие модели имеют много общего с иерархическими и сетевыми моделями.

Объекты описываются набором атрибутов (параметрами). Однотипные объекты описываются одними и теми же параметрами и могут быть объединены в классы.

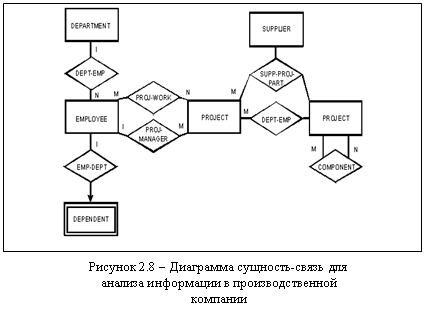
На ER-диаграммах сущности отображаются прямоугольниками, а связи – ромбами. Такие модели имеют много общего с иерархическими и сетевыми моделями.

При построении ЕR-модели важно учитывать разновидности объектов. Различают простые и сложные объекты.

Простой объект, если он имеет свойства атомарного объекта. Сложный объект – если он может быть представлен в виде совокупности простых объектов.

Сложные объекты бывают составными, обобщенными и агрегированными.

Составные объекты сгруппированы в виде связи «целое-часть».

Обобщенные объекты поддерживают отношения «тип-тип» или «род-вид»

Агрегированные объекты спроектированы на основе агрегации, например, в них участвуют объекты, связанные одним процессом.

Основными конструктивными элементами моделей являются сущности, связи между ними и их свойства.

Связь (relationship) – это ассоциация, устанавливаемая между сущностями. Например, «отец – сын» – это связь между двумя сущностями «человек». Выделяются два типа связей.

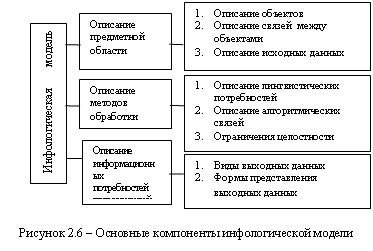
Первый тип связи – связь «один-к-одному» или (1:1): в каждый момент времени каждому представителю (экземпляру) сущности А соответствует 1 или 0 представителей сущности В. Например, работник и его ставка.

Второй тип – связь «один-ко-многим» или (1:М): одному представителю сущности А соответствуют 0, 1 или несколько представителей сущности В.

На основе этих двух видов связей можно составить более сложные связи. На рисунке 2.8 приведен пример ЕR-диаграммы для анализа информации в производственной компании6.

В) Иерархическая модель данных ГИС

Иерархическая модель – простейшая структурно-определенная модель данных, представляющая собой совокупность элементов, расположенных в порядке их подчинения от общего к частному. Связи между частями информационной модели – жесткие, структурная диаграмма – упорядоченное перевернутое дерево. Основные понятия: корень, ветвь, лист, уровень. В иерархической структуре элементы распределяются по уровням, от первого (верхнего) уровня до нижнего (последнего) уровня. На первом уровне может располагаться только один элемент, который является вершиной иерархической структуры или корнем. Основное отношение между уровнями состоит в том, что элемент более высокого уровня может состоять из нескольких элементов нижнего уровня, при этом каждый элемент нижнего уровня может входить в состав только одного элемента верхнего уровня.

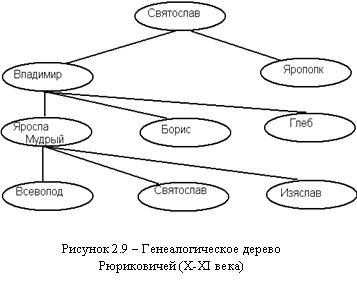Граф модели (схема) включает два основных элемента: дугу и узел. Узел соответствует представлению объектов, дуги – связям между ними, причем дуги должны быть ориентированы от корня к листьям, т. е. иерархическая модель – это ориентированный граф. Такой граф называют еще иерархическим деревом определения. Требование к иерархической структуре: между двумя узлами не может быть более одной дуги. Говорят, дуга исходит из родительского узла (порождающего) и входит в дочерний узел (порожденный). Типичным примером иерархической структуры может служить генеалогическое дерево (рис. 2.9).

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9