(мм).

Точность атрибутов определяется близостью значений атрибутов и их истинных величин. Атрибуты объекта могут со временем меняться. Точность атрибутов может быть разной в различных частях карты. Поэтому иногда пользуются обобщенными статистическими показателями.

Логическая непротиворечивость связана с внутренней непротиворечивостью структур данных, например, полигоны должны быть замкнуты, идентификаторы – уникальны и др., а также внутренней топологической непротиворечивостью. Например, подземный переход связывает две улицы, которые не соседствуют реально – это логическая противоречивость.

Полнота (или достаточность) данных связана со степенью охвата данными множества исследуемых объектов. При этом учитывают степень генерализации и масштаб представления территории.

Происхождение – специфический показатель, характерный для ГИС. Он учитывает источник данных, методы обработки данных, точность съема информации, погрешности расчетов и др.

2.6 Модели визуального представления информации в ГИС

Наиболее универсальными и чаще используемыми моделями пространственных данных в ГИС являются следующие:

-  векторное представление (точки, линии, полигоны);

-  векторно-топологическое представление;

-  векторно-нетопологическое или модель «спагетти»;

-  растровое представление (ячейки, сетки);

-  регулярно-ячеистое представление;

-  квадродерево (квадротомическое представление).

Все модели взаимно преобразуемы. На рис. 2.21 приведен пример векторной и растровой моделей местности.

Рисунок 2.21 – Примеры растрового и векторного

отображения местности

2.6.1 Векторная модель данных ГИС

Векторная модель данных (vector data model) или цифровое представление точечных, линейных и полигональных пространственных объектов в виде набора координатных пар, с описанием только геометрии объектов, что соответствует нетопологическоой модели. Векторно-нетопологическое представление данных в ГИС называют модель «спагетти». Векторным моделям соответствует векторный формат пространственных данных (vector data format).

Векторные модели строятся с использованием векторов, в которых каждая точка на карте определяется через ее удаленность от опорной точки и величину угла между направлением на точку из опорной точки и направлением на Север (по часовой стрелке). В векторных моделях ГИС описания объектов хранятся в памяти компьютера в виде математических формул и геометрических абстракций, таких как круг, квадрат, эллипс и подобных фигур. При построении векторных изображений создается целостный вид путем соединения точек линиями, дугами или полилиниями. Поэтому векторную модель называют объектной. Векторные изображения занимают значительно меньше памяти ЭВМ при хранении, чем растровые, требуют меньше затрат времени на обработку. Алгоритмы обработки, как правило, более просты.

Базовым примитивом векторных моделей ГИС является точка. Через понятие «точка» определяются все остальные объекты векторной модели.

Безразмерные типы объектов:

-  точка - определяет геометрическое местоположение объекта;

-  узел – топологический переход или конечная точка, также может определять местоположение объекта.

Одномерные типы объектов:

-  линия – одномерный объект;

-  линейный сегмент – прямая линия между двумя точками;

-  дуга – геометрическое место точек, которые формируют кривую, определенную математической функцией;

-  связь – соединение между двумя узлами;

-  направленная связь – связь с одним определенным направлением;

-  кольцо – последовательность непересекающихся цепочек, строк, связей или замкнутых дуг.

Двумерные типы объектов:

-  область – ограниченный непрерывный объект, который может включать или не включать в себя собственную границу;

-  внутренняя область – область, которая не включает собственную границу;

-  полигон (контур) – двумерный (площадной) объект, внутренняя область которого образована замкнутой последовательностью сегментов в модели «спагетти».

Различают простой полигон, не содержащий внутренних полигонов, и составной полигон, содержащий внутренние полигоны, называемые также «островами» (island ) и анклавами (hole).

Каждый участок линии может быть границей пересечения двух полигонов, каждый из которых может иметь свои отличные от другого атрибуты. Поэтому эти полигоны по отношению к линии именуются «левый» и «правый».

Векторное изображение можно получить различными способами. Наиболее часто используют векторизацию сканированного (растрового) изображения. Векторизация заключается в распознавании на растровом изображении объектов, выделение их, представление каждого объекта в векторном формате. Для автоматической векторизации необходимо иметь изображения высокого качества, часто приходится заниматься исправлением исходного или/и векторного изображений.

К особенностям векторных моделей можно отнести следующие:

-  в векторной модели легко осуществляются некоторые операции с объектами, например, разбивка объекта (речной сети) на участки, замена условных обозначений;

-  легко проводятся изменение масштаба, повороты, растягивание и другие операции;

-  векторные модели имеют преимущество перед растровыми моделями в точности представления точечных объектов.

2.6.2 Топологические модели

Разновидностью векторных моделей являются топологические модели. Топологические модели объединяет «взаимосвязанность» объектов, которая бывает простой или сложной. Топологические свойства фигур не изменяются при деформациях, производимых без разрывов или соединений (рис. 2.22).

Термин топологический в ГИС понимают так, что в моделях объектов хранятся взаимосвязи, которые расширяют возможности использования данных ГИС для различных видов пространственного анализа. Например, в логическую структуру описания данных вводится информация о том, какие линии и в каких точках пересекаются, из чего состоит полигон и др.

Теоретической основой представления топологических моделей является теория графов. Топологические модели позволяют представить всю карту в виде графа. Площади, линии и точки описываются с помощью узлов и дуг. Каждая дуга идет от начального к конечному узлу. Известно, что находится справа и слева.

Необходимая процедура при работе с топологическими данными – подготовка геометрических данных. Этот процесс практически не может быть автоматизирован: топологические характеристики должны быть вычислены заранее и занесены в базу данных вместе с координатными данными.

Какие характеристики свойственны топологическим моделям?

1.   Связанность контуров – это означает, что контуры должны храниться не как совокупность отдельных точек, а как взаимосвязанные друг с другом объекты, например, имея карту автодорог, можно определить возможность проехать из точки А в точку Б.

2.   Связанность и примыкание районов – это информация о взаимном расположении районов и об узлах пересечения на них.

3.   Пересечение – информация о типах пересечений, которая позволяет «строить» на картах автомобильные развязки, мосты и др.

4.   Близость – показатель пространственной близости линейных или полигональных объектов. Оценивается числовым параметром.

Топологические характеристики линейных объектов могут быть представлены в виде графа со всеми узлами и пересечениями. Примерами таких графов могут служить схема трамвайных маршрутов; схема метрополитена. Узлы графа соответствуют пересечениям дорог, ребра описывают участки дорог. Длина ребер может и не нести информативной нагрузки.

Топологические характеристики полигональных объектов могут быть представлены в виде графов покрытий и смежности. Граф покрытия гомоморфен контурной карте соответствующей местности. Ребра графа – границы районов, узлы – точки смыкания районов. Степень вершины такого графа – число районов, которые в ней смыкаются.

Общепринятым является деление векторных программных средств ГИС на топологические и нетопологические. В первых ГИС фиксация топологических пространственных отношений между объектами (смежности, связности, вложенности и др.) является основой их конструкции. Во вторых же ГИС цифруются пространственные объекты, изначально не знающие друг о друге, и построение отношений между ними осуществляется в режиме постпроцесса. Топологические системы являются более адекватным инструментом для создания качественных цифровых карт. Практика ГИС показывает, что значительно выгоднее, когда оператор создает изначально качественные карты и фиксирует в них отношения между объектами, а не относит эту стадию на этап постпроцесса.

Топологические характеристики заносятся при кодировании данных в виде дополнительных атрибутов. Во многих ГИС это производится при дигитализации полуавтоматически.

Практически все используемые в настоящее время ГИС используют топологические модели, что позволяет хорошо выражать пространственное соотношение между объектами.

2.6.3 Растровые модели

В растровых моделях дискретизация непрерывных последовательностей реального мира осуществляется наиболее простым способом: вся территория представляется последовательностью ячеек (пикселей), образующих регулярную сеть. Каждой ячейке соответствует одинаковый по размеру, но разный по характеристикам участок территории. В ячейке модели содержится значение характеристик, усредненные по участку территории (рис. 2.23). Процедура формирования изображения называется пикселизация.

Если векторная модель дает представление, «где» находится объект, то растровая модель – «что» расположено в той или иной точке территории.

В качестве атомарной модели используется элементарный участок территории – пиксель. Упорядоченная последовательность пикселей образует растр, который является моделью карты. Каждый элемент растра имеет одно значение плотности или цвета.

Характеристики растровых моделей:

-  разрешение;

-  значение;

-  ориентация;

-  зона;

-  положение.

Разрешение – минимальный линейный размер наименьшего участка пространства или поверхности, отображаемый одним пикселем. Пиксель чаще всего изображается прямоугольником или квадратом (иногда шестиугольником).

Значение – элемент информации, хранящийся в пикселе. В качестве типов значений могут использоваться разные классы значений: цифровые, буквенные и др. Например, 1 – класс незагрязненной среды; 2 – среда подвергнута антропогенному загрязнению; 3 – зона экотоксикологической опасности. Для отображения значения чаще всего используются заливка пикселя (цветом, плотностью или узором).

Ориентация определяется через угол между направлением на Север и положением колонок растра.

Зона – это соседствующие друг с другом ячейки, имеющие одинаковые значения. Зоны могут присутствовать не во всех слоях. Основные характеристики зоны – значение и положение.

Буферная зона – зона, границы которой удалены на известное расстояние от любого объекта на карте.

Положение задается упорядоченной парой координат, которые однозначно отображают положение каждого элемента на карте.

Достоинства растровых моделей:

-  растр не требует предварительного ознакомления с предметной областью; данные собираются с равномерно расположенной сети точек, могут легко подвергаться статистической обработке;

-  растровые модели просты в обработке, возможна обработка по параллельным алгоритмам, за счет чего обеспечивается высокое быстродействие;

-  некоторые задачи, например, создание буферной зоны, проще решаются в растровом виде;

-  многие растровые модели позволяют вводить векторные объекты, обратная задача много труднее;

-  процессы растеризации проще процессов векторизации алгоритмически.

Основные недостатки растровых моделей:

- требуют больших объемов (по сравнению с векторными моделями) памяти для хранения изображения;

- растровые объекты сложно масштабировать: при увеличении объекта становятся видны отдельные пиксели, контуры изображения теряют гладкость, изображение становится зернистым;

- сложно рассчитать результирующий цвет пикселя, который получается при слиянии нескольких пикселей разных цветов;

- проблемы разбиения сложного изображения на произвольные элементы для их раздельного использования и редактирования.

Наиболее часто растровые модели получают при обработке космических снимков. Самый простой способ ввода растрового изображения – прямой ввод информации ячейка за ячейкой. Недостаток такого метода: значительное время, затрачиваемое на ввод. Кроме того, растровые цифровые изображения занимают, как правило, большие объемы памяти. Например, при обработке снимков с искусственного космического спутника Земли каждый снимок разбивается на сотни миллионов пикселей. Однако часто информация в нескольких ячейках, идущих подряд, повторяется (т. е. формируются зоны). Возникает возможность сжатия информации при вводе. Один из методов сжатого представления растровой информации – метод группового кодирования.

Метод группового кодирования (run-length encoding, run lenght coding, RLE) – кодирование группами отрезков. Это самый простой и распространенный из методов сжатия растровых данных, основанный на замене групп повторяющихся символов в последовательности значением числа повторений, иначе говоря, замена отрезка, состоящего из одноименных элементов растра, длиной отрезка (run length).

В методе группового кодирования данные вводятся парой чисел: первое обозначает длину группы пикселей, имеющих одинаковое значение, второе – значение пикселя в этой группе. Данные вводятся построчно. Если элемент встречается впервые – он помечается признаком «начало». Если за данной ячейкой следует цепочка ячеек с такими же значениями, то они подсчитываются. Последняя ячейка помечается признаком «конец». Ввод осуществляется справа налево, сверху вниз.

Например, символ – треугольник, составленный из символов «1». Исходный растр содержит 28 символов.

0001000

0011100

0111110

0000000

Закодированный растр: , т. е. 20 символов. Даже на таком маленьком примере видно преимущество: вместо 28 символов используется 20, т. е. выигрыш около 30%. При работе с большими массивами экономия места и времени еще значительнее.

Контрольные вопросы к теме 2

1.  Поясните понятие «генерализация».

2.  Чем отличается генерализация от агрегации?

3.  Что является самой элементарной информационной единицей?

4.  Что такое атрибут?

5.  Чем отличается логическая запись от физической?

6.  Дайте определение классификации.

7.  Приведите пример классификации 1 типа.

8.  Приведите пример классификации 2 типа.

9.  Что такое эталон класса?

10.  Объясните принцип работы алгоритма «Форель».

11.  Как с помощью алгоритма «Форель» получить заданное число классов?

12.  Объясните принцип работы алгоритма «Краб».

13.  Что такое «гиперсфера»?

14.  Какие характеристики классификации учитываются в критерии качества алгоритма «Краб»?

15.  Для чего используются в ГИС представители классов?

16.  Чем отличаются дивизимные алгоритмы классификации от агломеративных?

17.  Почему алгоритм «Краб» относится к вариационным алгоритмам?

18.  Как определить центр тяжести класса?

19.  Как определяется мера близости точек в классе в алгоритме «Краб»?

20.  Можно ли автоматическую классификацию считать объективной?

21.  Чем отличаются сильно типизированные модели данных от слабо типизированных? Приведите примеры.

22.  Что такое «инфологическая модель данных»?

23.  Какие три компоненты составляют инфологическую модель ГИС?

24.  Что такое «уровень узла» в иерархической модели?

25.  Для чего в ГИС может быть использовано квадратомическое дерево?

26.  Что такое первичный ключ отношений?

27.  Какими свойствами должен обладать ключ в реляционной модели данных?

28.  Что такое «геоид»?

29.  Чем отличаются плоские декартовы координаты от плоских полярных координат?

30.  Чем отличается малый круг на Земной поверхности от большого круга?

31.  Какие примитивы обычно используют в ГИС?

32.  Чем отличается нормальный узел от псевдоузла?

33.  Чем характеризуется висячий узел?

34.  Какие типы взаимосвязей могут существовать между координатными данными?

35.  Что называется валентностью узла?

36.  Что такое «разграфка» топографической карты?

37.  Карты какого масштаба являются топографическими?

38.  Чем отличается колонна от зоны при разграфке топографических карт?

39.  Определите номенклатуру листа масштаба 1:, на котором находится объект с географическими координатами 300 С. Ш. 700 В. Д.

40.  Приведите пример номенклатуры листа масштаба 1:25 000.

41.  Какие характеристики определяют качество данных?

42.  Что понимают под логической непротиворечивостью?

43.  Чему равна позиционная погрешность данных, если ошибка съема данных равна 1 мм, ошибка цифрования составляет 0,8 мм, а ошибка представления равна 0,4 мм?

44.  По каким характеристикам векторная модель превосходит растровую модель?

45.  Чем отличается топологическая модель от нетопологической?

46.  Может ли растровая модель быть топологической?

47.  Назовите основные характеристики растровой модели.

48.  В чем суть метода группового кодирования?

49.  Можно ли при классификации по алгоритму «Форель» получить пустой класс?

50.  Для чего в алгоритме классификации используется кратчайший незамкнутый путь?

Тема 3. Основные виды операций над координатными данными

3.1 Векторизация

Координатные данные могут быть представлены в векторном, либо в растровом форматах. Растровые изображения отображают поля данных, т. е. носят полевой характер. Векторные изображения изображают объекты, т. е. носят объектный характер. Каждый вид изображения имеет свои преимущества, поэтому в ГИС используются оба вида. Растровые изображения часто используются на стадии ввода, векторные – при обработке и выдаче результатов. Растровыми изображениями являются основные входные документы: фотографии, карты, архивные данные. Операции преобразования данных из растрового представления в векторное изображение называется векторизацией. В технологическом плане данная операция представляет собой переход от полевого изображения к объектному.

Чаще всего векторизацию применяют при интерпретации сканированных аэрокосмических снимков. Для этого на растровом изображении выделяют и оконтуривают однородные области, затем придают им свойства объектов.

Векторные изображения могут быть сразу созданы с помощью специальных программ – графических редакторов, которые входят в состав большинства ГИС-пакетов. Для векторизации растровых изображений существуют специальные программы – векторизаторы и устройства векторизации.

Векторизация может быть ручной, полуавтоматической и автоматической. В графических редакторах обычно используется ручная векторизация, так как при построении изображений одновременно решается задача идентификации объектов и присвоение им пользовательских идентификаторов. Автоматические и полуавтоматические векторизаторы служат для обработки электронных растровых изображений, ручной режим в них служит лишь для коррекции результата. Для ручного ввода векторных объектов используется устройство – дигитайзер. Дигитайзер представляет собой планшет, на котором располагается оригинал-растр. Специальным «карандашом» оператор обводит контуры объектов, при этом формируются векторные примитивы в виде линий (полилиний), если контур объекта не замкнут, полигонов (контур замкнут) и точек.

Программы – векторизаторы различаются следующими характеристиками:

-  возможностью векторизации различных видов растра: бинарного, полутонового, цветного изображений;

-  требуемым качеством исходного растра;

-  возможностью редактирования исходного растрового изображения;

-  типом графической оболочки.

Задачей векторизации является не только выделение объектов, но и сохранение топологии. Например, линия со стрелками должна быть распознана как линия со стрелками, а не как совокупность трех отдельных линий; две пересекающиеся линии – как две линии, а не как четыре отрезка.

При работе в автоматическом режиме векторизации до сих пор существует много проблем: подавление шумов, нахождение и устранение разрывов линий, учет изменения толщины линии, сохранение топологических признаков, распознавание и восстановление надписей, анализ ситуаций с большим количеством объектов и др.

Пока самым надежным и точным является интерактивный метод, когда программа-векторизатор в каждом сложном случае представляет оператору возможность принятия решения.

При векторизации применяют ряд специальных терминов:

· векторный объект – графический объект, заданный своим аналитическим описанием, которое включает в себя тип векторного объекта (его форму: отрезок прямой, окружность, дуга и др.), а также параметры объекта (координаты базовых точек, масштаб и др.);

· векторный рисунок – совокупность векторных объектов;

· маска – прямоугольная область растрового изображения, задаваемая пользователем, которая игнорируется при векторизации;

· примитив – простейшая графическая модель векторизации (дуга, линия, текст, контур, полилиния, размерная линия);

· рабочая область – прямоугольный фрагмент растрового изображения, который обрабатывается программой-вектори-затором;

· файл параметров – уникальный для каждого растрового изображения файл, который содержит все параметры распознавания: информацию о расположении рабочей области, значение разрешения растрового изображения (точек на дюйм), текущие единицы (точки, миллиметры, дюймы);

· фильтрация – процедура, применяемая для повышения качества растрового изображения; программа фильтрации анализирует цвет близлежащих точек вокруг обрабатываемой точки и изменяет или оставляет без изменения ее цвет.

Легче всего программы-векторизаторы обрабатывают бинарные изображения. Когда растровое изображение выводится на монитор, каждый пиксель экрана соответствует нескольким растровым точкам изображения. Цвет пикселя становится черным или белым в зависимости от того, каких точек (черных или белых) в нем больше. Черные пиксели, сливаясь в зоны, образуют пятна, из которых формируются полигоны и линии, которые, в свою очередь, передают изображение рисунка.

При векторизации можно управлять режимом отображения растрового изображения, используя команды управления экраном. При отображении «один к одному» программа отобразит один элемент растра в один пиксель. При отображении «один к двум» – изображение на экране будет увеличенным, при этом для изображения каждой растровой точки используется четыре пикселя. При этом вид растрового изображения может исказиться: неровности, не заметные при прежнем масштабе, увеличатся пропорционально и будут сильно видны.

3.2 Проекционные преобразования

Земля – круглая[7], карта – абсолютно плоская. Возникает задача: круглую Землю отобразить на плоской карте, при этом спроецировать ее так, чтобы можно было установить математическое соответствие между географическими координатами объектов на Земле и плоскими координатами этого же объекта на бумаге (экране монитора). Для обеспечения математического соответствия применяются проекционные преобразования. За большинством видов проекций стоит достаточно простой математический аппарат, переводящий географические координаты на эллипсоиде Земли в прямоугольные координаты на бумаге.

Математический закон построения карты требует задания масштаба и вида картографической проекции.

3.2.1 Масштаб

Уменьшая мысленно земной эллипсоид в М раз, например, враз, получают его геометрическую модель – глобус, изображение которого уже в натуральную величину на плоскости дает карту поверхности эллипсоида. Величина 1: М (в примере 1:определяет главный, или общий масштаб карты.

Масштабом называется отношение длины линии на карте к длине соответствующей линии на Земном шаре.

Масштаб показывает, во сколько раз уменьшено картографическое изображение, сколько сантиметров на местности содержится в 1 см на карте. Например, масштаб 1:1 означает, что 1 см на карте соответствует 1000000 см на местности, т. е. в 1 см карты – 10 км на местности.

Так как поверхности эллипсоида и шара не могут быть развернуты на плоскость без разрывов и складок (они не принадлежат к классу развертывающихся поверхностей), любой карте присущи искажения (например, длин линий, углов и т. п.). Основная характеристика карты в любой ее точке – частный масштаб μ. Это величина, обратная отношению бесконечно малого отрезка dS на земном эллипсоиде к его изображению dσ на плоскости:

,

причем μ зависит от положения точки на эллипсоиде. Как правило, , равенство возможно лишь в отдельных точках или вдоль некоторых линий на карте. Таким образом, главный масштаб карты характеризует ее только в общих чертах, в некотором осредненном виде.

Отношение называют относительным масштабом, или увеличением длины, разность 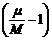называют искажением длины. При анализе свойств картографической проекции можно не принимать во внимание главный масштаб; численное значение его учитывается только при вычислениях координат точек на карте.

Как правило, на картах дают не только числовой, но и линейный масштаб – отрезок масштабной линейки, удобный для выполнения измерений.

В России приняты следующие масштабы топографических карт: 1:1 , 1:, 1:, 1:, 1:50 000, 1:25 000, 1:10 000. Этот ряд масштабов называется стандартным. Иногда в этот ряд включат вспомогательные масштабы 1:, 1:5000 и 1:2000.

Карты масштабов 1:50 000 (1см = 500 м), 1:см = = 1000 м) называются крупномасштабными. Карты масштабов 1:10 000 (1см =100 м), 1:25 000 (1см = 250 м) называются планами.

3.2.2 Картографическая проекция

Картографическая проекция – это способ перехода от реальной, геометрически сложной земной поверхности к плоскости карты. Для этого вначале переходят к математически правильной фигуре (конус, цилиндр), а затем изображение проектируется на плоскость, опять-таки с помощью строгих математических правил.

Сферическую поверхность невозможно развернуть на плоскость без деформаций – сжатий и растяжений. Значит, всякая карта имеет те или иные искажения. Различают искажения длин, площадей, углов и форм. На крупномасштабных картах искажения могут быть практически неощутимы, но на мелкомасштабных они бывают очень велики. Картографические проекции обладают разными свойствами в зависимости от характера и размера искажений.

Равноугольные (конформные) проекции сохраняют без искажений углы и формы малых объектов, зато в них резко деформируются длины и площади объектов. По картам в равноугольных проекциях удобно, например, прокладывать маршруты судов и самолетов, но невозможно измерять площади.

Равновеликие (эквивалентные) проекции не искажают площадей, но углы и формы объектов в них сильно искажены. Эти проекции хорошо приспособлены для определения площадей (например, размер государств, земельных угодий и др.).

Произвольные проекции имеют искажения длин, площадей и углов, но они распределяются по карте наиболее выгодным образом. Например, выбирают проекции с минимальными искажениями в центральной части, зато они резко возрастают по краям карты. Среди произвольных проекций выделяются равнопромежуточные, в которых искажения длин отсутствуют по одному из направлений: либо вдоль меридиана, либо вдоль параллели.

Кроме того, существует большой класс условных проекций, при построении которых не пользуются геометрическими аналогиями, а лишь математическими уравнениями нужного вида.

Преобразования картографических проекций используются тогда, когда цифровая карта (или слой) выполнена в некоторой известной проекции или месторасположение объектов соответствуют их теоретическим координатам, но должны быть преобразованы в географические координаты либо в другую картографическую проекцию. Координаты точек пространственных объектов на компьютерной карте должны однозначно определять местоположение объектов на земной поверхности.

Группа процедур, осуществляющая переход от одной проекции к другой, носит название проекционные преобразования. Эти процедуры включают в себя как простые операции, например, пересчет координат при повороте, смещении, масштабировании, так и сложные операции (укладка объектов в систему опорных точек). В разных пакетах ГИС число операций проекционного преобразования различно: от сотен до их отсутствия. Например, в ГИС ГеоГраф – несколько десятков, а в ArcInfo- сотни преобразований.

Проекции различают и по виду вспомогательной поверхности, используемой при переходе от эллипсоида или шара Земли к плоскости карты. Основные виды проекций, используемых в ГИС:

-  конические;

-  азимутальные;

-  цилиндрические;

-  поликонические;

-  видоизмененные поликонические;

-  псевдоцилиндрические;

-  Гаусса-Крюгера.

По положению полюса сферических координат проекции бывают:

-  нормальные (прямые);

-  поперечные;

-  косые.

Географические координаты (угловые величины: широта и долгота) определяют положение любой точки относительно экватора и начального (Гринвичского) меридиана. На карту наносятся линии параллелей и меридианов. Параллель – это любая линия, все точки которой имеют одну и ту же географическую широту. Счет параллелей идет от экватора к северу и югу (от 0° до 90° северной или южной широты). Меридиан – это линия, все точки которой имеют одинаковую географическую долготу. По отношению к Гринвичскому меридиану различаются западные и восточные долготы (з. д. и в. д.), отсчитываемые от 0° и 180°.

Линии меридианов и параллелей образуют картографическую сетку. Обычно на рамках карты подписывают значения основных меридианов и параллелей, иногда дают более дробные деления (например, через 5° или через 1°) для удобства отсчета координат.

За большинством видов проекций стоит достаточно простой математический аппарат, переводящий географические координаты на эллипсоиде Земли в прямоугольные координаты на бумаге.

По форме координатных линий наиболее универсальной является прямоугольная система декартовых координат: x, y, z. Но при решении задач картографии, навигации и др. необходимо использовать координатную поверхность отсчетного эллипсоида и связанные с ней геодезические (эллипсоидные) координаты B(широту), L (долготу) и H(высоту над уровнем моря)[8]

Связь прямоугольных и геодезических координат описывается выражениями

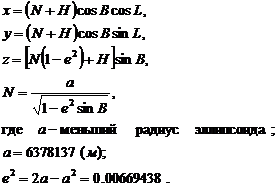
А) Конические проекции

Наибольшее распространение в картографии получили равноугольные и равновеликие конические проекции. Образование конических проекций для наглядности можно представить как проектирование земной поверхности на боковую поверхность конуса, определенным образом ориентированного относительно земного шара (эллипсоида). В прямых конических проекциях оси земного шара и конуса совпадают. При этом берется или касательный конус (рис. 3.1, А) к эллипсу земной поверхности, или секущий (рис. 3.1, В). После проектирования боковая поверхность конуса разрезается по одной из образующих и развертывается в плоскость.

В зависимости от размеров изображаемой территории в конических проекциях получаются одна или две параллели, вдоль которых сохраняются длины без искажений. Эти параллели называются стандартными. Одну стандартную параллель в проекции получают при использовании касательного конуса (рис. 3.1, А). Такая проекция применяется при анализе территории с небольшой протяженностью по широте. Две стандартных параллели (рис. 3.1, В) получают при использовании секущего конуса.

В математическом описании конических проекций имеются две постоянные величины «r» и «c» (рис. 3.2). Постоянная «r» равняется синусу широты стандартной параллели или, что то же самое, синусу угла при вершине конуса. Для проекций с двумя стандартными параллелями формула остается верной только для равноугольных проекций, причем в этом случае j – широта параллели с наименьшим масштабом (верхняя). Из формулы следует, что постоянная «r» может быть только меньше единицы 0r1. Если же r=1, то коническая проекция превратится в азимутальную. Если r0, то образующие конуса будут параллельны его оси и коническая проекция превратится в цилиндрическую.

Вторая постоянная «с» в равноугольной и промежуточной проекции имеет определенный геометрический смысл – это радиус экватора в проекции.

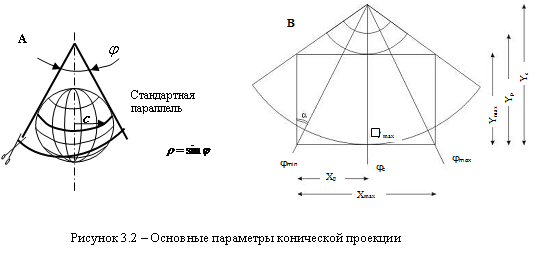Коническая проекция будет вполне определена, если заданы постоянные величины проекции или «любые величины, взаимно однозначно с ними связанные». Это могут быть широты стандартных или крайних параллелей. В последнем случае, например, может быть дополнено условие, чтобы масштабы на крайних параллелях и на параллели с наименьшим масштабом были равны по абсолютной величине. Может быть поставлено, например, требование, чтобы среднее квадратичное искажение длин было наименьшим или было наименьшим крайнее искажение углов. Наиболее просто постоянные проекции вычисляются по заданным значениям широт стандартных параллелей j1 и j2. Выбирать их следует в соответствии с конфигурацией изображаемой области.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9