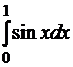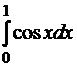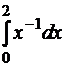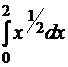Лабораторный практикум по дисциплине «Системный анализ и математическое моделирование процессов в машиностроении» (стр. 1 )

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Уфимский государственный авиационный технический университет

Кафедра технологии машиностроения

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

по дисциплине

«Системный анализ и математическое моделирование

процессов в машиностроении»,

Уфа 2010

Составитель

УДК 519.87:

ББК 22.18:34.4 (я7)

Лабораторный практикум по дисциплине «Системный анализ и математическое моделирование процессов в машиностроении» / Сост.: ; Уфимск. гос. авиац. техн. ун-т. – Уфа, 2010. – 47 с.

Содержит описание пяти лабораторных работ, посвященных изучению методов математического моделирования при решении технических и технико-экономических задач машиностроения, основанных на математическом программировании, имитационном моделировании, теории массового обслуживания, многокритериальной оптимизации и статистическом моделировании.

Предназначен для студентов направления 651«Машиностроительные технологии и оборудование», специальность 120«Машины и технологии высокоэффективных процессов обработки материалов»

Табл.6 Библиогр.: 20 назв.

Рецензенты: д-р техн. наук, проф.

д-р техн. наук, проф.

© Уфимский государственный

авиационный технический университет, 2010

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

Лабораторный практикум включает пять лабораторных работ по дисциплине «Системный анализ и математическое моделирование процессов в машиностроении». В соответствии с учебным планом специальности «Машины и технологии высокоэффективных процессов обработки материалов» на выполнение лабораторных работ предусмотрено 16 часов.

Трудоемкость выполнения лабораторных работ составляет: №1 – 4 часа, №2 – 4 часа, №3 – 4 часа, №4 – 2 часа, №5 – 2 часа, итого – 16 часов.

В представленных лабораторных работах рассматриваются важные разделы дисциплины: статистическое моделирование (метод Монте-Карло), модели на основе массового обслуживания, имитационное моделирование, методы одно - и многокритериальной структурной оптимизации, модели и оптимизация на основе математического программирования.

Автором были написаны лабораторные работы №№1, 3, 4 и существенно переработаны лабораторные работы №№ 2 и 5 , составленные ранее , .

ЛАБОРАТОРНАЯ РАБОТА №1

СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

1.1. ЦЕЛЬ РАБОТЫ

Целью работы является ознакомление студентов с возможностями метода статистического моделирования – метода Монте-Карло.

Метод Монте-Карло в лабораторной работе используется для решения двух задач:

- нахождения определенного интеграла функции (цель – получение общих представлений о методе)

- моделирования работы робототехнического комплекса

Работа состоит из двух соответствующих частей, посвященных рассматриваемым задачам.

1.2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Метод Монте-Карло является методом статистического моделирования. Его применение эффективно там, где сложно или невозможно построение аналитической модели. Например, в системах массового обслуживания, не являющихся марковскими системами, в задачах надежности, управления, экономики и т. п., вообще, для сложных систем, которые состоят из большого числа взаимодействующих элементов.

Идея метода заключается в следующем. Вместо того, чтобы оттсывать процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений), производится «розыгрыш» случайного явления с помощью специально организованной процедуры, включающей в себя случайность и дающей случайный результат реализации процесса. Множество реализаций можно использовать как некий искусственно полученный статистический материал, который может быть обработан обычными методами математической статистики и получены интересующие нас статистические характеристики. При моделировании случайных явлений методом Монте-Карло мы пользуемся самой случайностью как аппаратом исследования.

В математике метод Монте-Карло применяется для вычисления интегралов, особенно многомерных, для решения систем алгебраических уравнений высокого порядка и т. п.

Метод Монте-Карло имеет простую структуру вычислительного алгоритма. Как правило, составляется программа для осуществления одного случайного испытания. Затем это испытание повторяется N раз, причем каждый опыт не зависит от всех остальных, и результаты всех опытов осредняются. Поэтому метод Монте-Карло называют также методом статистического моделирования.

Погрешность вычисления метода, как правило, пропорциональна , где D – некоторая постоянная, N – число испытаний. Отсюда видно, что для того, чтобы уменьшить погрешность в 10 раз, нужно увеличить N в 100 раз.

Приведем важное для метода Монте-Карло соотношение:

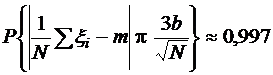, (1.1)

где - случайная величина; m – неизвестная искомая величина (статистическую оценку которой необходимо получить); b – среднеквадратичное отклонение случайной величины (одинаково для всех ).

Соотношение (1.1) дает нам метод расчета m и оценку погрешности. В самом деле, найдем N значений случайной величины . Из (1.1) видно, что среднее арифметическое этих значений будет приближенно равно m. С большой вероятностью погрешность такого приближения не превосходит величины . Очевидно, эта погрешность стремится к нулю с ростом N.

В рассматриваемой работе требуется определить среднее время работы РТК. При этом известны интенсивность потока отказов и схема поточной линии.

Известно, что поток отказов подчиняется экспоненциальному (показательному) закону распределения с плотностью распределения

,

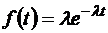где - интенсивность потока отказов (число отказов в сутки); t –последовательности значений продолжительности интервалов между отказами.

Требуется смоделировать случайную величину, распределенную в соответствии с экспоненциальным законом.

Существует основное соотношение, связывающее случайные числа с заданным законом распределения и случайные числа с равномерным законом распределения в интервале [0,1]. Суть его состоит в том, что для преобразования последовательности случайных чисел с равномерным законом распределения в интервале [0,1] в последовательность случайных чисел с заданной функцией распределения необходимо из совокупности случайных чисел с равномерным законом распределения выбрать случайное число и решить уравнение

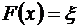
относительно x.

Для случая экспоненциального распределения выразим через

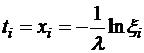. (1.2)

Значения определяем по генератору случайных чисел в MS EXCEL (или другой программе) или по таблице случайных чисел.

Рассмотрим применение метода Монте-Карло для статистической оценки некоторого определенного интеграла

,

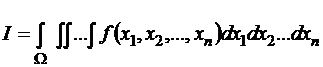где - область в n-мерном пространстве.

В лабораторной работе для простоты вычислений рассматривается определенный интеграл от функции одной переменной

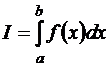(3)

Требуется найти его статистическую оценку . Задача сводится к оценке отношения площади криволинейной трапеции, соответствующей некоторому определенному интегралу, к площади квадрата, в который этот интеграл может быть вписан, т. е. имеющий координаты: (а, 0), (b, 0), (а, b-а), (b, b-а).

Идея метода заключается в следующем. Выберем пару случайных чисел х: и у: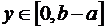– их можно рассматривать как координаты случайной точки в указанном квадрате. Затем выберем следующую пару чисел и т. д. Когда число выбранных таким образом точек станет достаточно большим, они более-менее равномерно покроют данный квадрат. При этом множество точек N, попавших под кривую , будет пропорционально площади криволинейной трапеции, а множество всех точек M – площади квадрата.

Тогда статистическая оценка искомого интеграла найдется по формуле

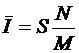, (1.4)

где S – площадь квадрата со стороной b-а.

Погрешность (абсолютная) может быть найдена из разности:

(1.5)

1.3. ЗАДАНИЕ И МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ

Задание по лабораторной работе состоит из двух частей. В первой части для общего ознакомления с методом статистического моделирования рассматривается задача нахождения определенного интеграла. Во второй части рассматривается практическая задача определения среднего времени безотказной работы робототехнического комплекса (РТК).

3.1.Вычисление определенного интеграла методом Монте-Карло

Задание

Выбрать вариант интеграла функции 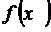по указанию преподавателя из таблицы 1.1

Таблица 1.1

Вариант выбора определенного интеграла

Требуется:

1) вычислить определенный интеграл функции методом Монте-Карло;

2) определить зависимость точности метода в зависимости от мощности множества М.

Методика выполнения работы

1) Сгенерируем множество М точек на плоскости внутри квадрата с координатами (а, 0), (b, 0), (а, b-а), (b, b-а). Каждая точка имеет координаты. Генерация множества М производится путем использования Microsoft Excel при числе параметров 2 , M = 50 и заданных границах. (рис.2)

C D

A Xi B

Рис. 1.1. Схема оценки определенного интеграла

2) Для каждой абсциссы точки определяем статистическую оценку функции , которую обозначим через

3) Вычислим для каждой точки разность -.

4) Если - - точка принадлежит криволинейной трапеции, т. е. находится под кривой 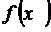. Найдем множество N элементов , для которых выполняется условие: -

5) Статистическая оценка искомого интеграла по методу Монте-Карло найдется по формуле (1.4)

6) Определим погрешность метода Монте-Карло по формуле (1.5).

7) Для определения зависимости зададимся рядом множеств : 50;100; 150 и определим в каждом случае .

8) Построим график зависимости в Microsoft Excel.

3.2. Определение среднего времени безотказной работы РТК

Задание

В таблице 1.2 задана интенсивность потока отказов для оборудования РТК.

Таблица 1.2.

Наименование оборудования РТК и интенсивность потока отказов

Задана схема организации поточной линии, изображенная на рис. 1.2.

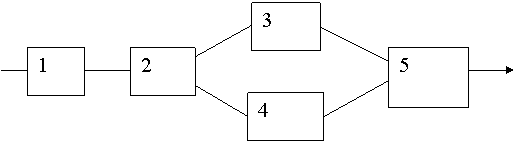
Рис.1.2. Схема организации поточной линии

При отказе хотя бы одного вида оборудования линия останавливается.

Требуется найти среднее время безотказной работы РТК.

Методика выполнения работы

Для каждого j-го вида оборудования (j=1,5) рассчитываются п. п 1-3:

1) Выбираем N случайных чисел в интервале [0,1]: .

Рекомендуется принять N=50.

2)Находим по формуле (1.2) при заданной интенсивности потока (таблица 1.2): .

3)Находим среднее время безотказной работы j-го вида оборудования

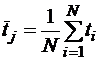
4)Вычисляем среднее время безотказной работы РТК. Для схемы, изображенной на рис.1.2, оно определяется по формуле

(1.6)

4.СОДЕРЖАНИЕ ОТЧЕТА

В отчете необходимо представить по первой части работы:

1) краткие теоретические сведения;

2) таблицы со сгенерированными случайными числами мощностью множества М = 50; 100 и 150;

3) диаграмму зависимости модуля абсолютной ошибки вычислений от М;

4)выводы по первой части работы.

По второй части работы:

1)таблицу со сгенерированными случайными числами при N = 50;

2) таблицу расчета величин ;

3) расчет среднего времени безотказной работы РТК;

4) выводы по второй части работы.

1.5. КОНТРОЛЬНЫЕ ВОПРОСЫ

1) Области применения метода Монте-Карло (статистического моделирования).

2)От каких условий зависит точность метода Монте-Карло?

3)Как изменится расчетная формула (6) при последовательном расположении оборудования РТК?

4)Можно ли находить с помощью метода Монте-Карло площади фигур в многомерной области?

СПИСОК ЛИТЕРАТУРЫ

1. Введение в математическое моделирование: Учеб. Пособие / под ред. . – М.: Университетская книга, Логос, 2007. – 440 с.

2. Вентцель операций. Задачи, принципы, методология. Учеб. Пособие для студентов втузов.- 2-е изд., стер. – М.: Высш. шк., 2001. – 208 с.

3. Щипачев анализ и математическое моделирование процессов в машиностроении: учебное пособие / ; Уфимск. гос. авиац. техн. ун-т.- Уфа, 20с.

4. Гмурман вероятностей и математическая статистика: Учеб. Пособие для вузов / . – 9-е изд., стер. – М.: Высш. шк., 2003. – 479 с.

5. Соболь Монте-Карло / – 4-е изд. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 80 с.

6.Соболь методы Монте-Карло / – М.: Наука. Главная редакция физико-математической литературы, 1973. – 312 с.

7. , Бережной методы моделирования экономических систем: Учеб. пособие / , –М.: Финансы и статистика, 2002. – 368 с.

ЛАБОРАТОРНАЯ РАБОТА №2

МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ

ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ОБРАБОТКИ ДЕТАЛЕЙ

2.1. ЦЕЛЬ РАБОТЫ

Целью лабораторной работы является получение практических навыков проведения оптимизации технологических процессов (одно - и многокритериальной) на различных иерархических уровнях по различным критериям.

2.2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Технологический процесс является иерархической системой с детерминированной структурой. Не представляет трудностей исследование структуры, т. к. она является искусственно созданной.

Технологический процесс разделяется на этапы, операции, технологические переходы, установы, ходы.

В пределах рассматриваемого иерархического уровня элементы этого уровня связаны друг с другом, что может быть отражено в виде соответствующего сетевого графа.

Нас в основном интересует уровень операций, поскольку операция является основным структурным элементом технологического процесса.

Граф, отображающий последовательность выполнения операций техпроцесса, является, как правило, многовариантным – см. рис.2.1.

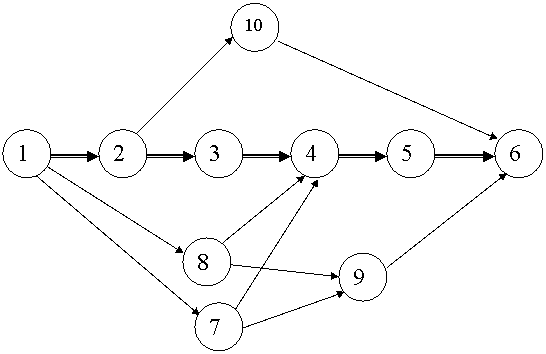
Рис.2.1. Пример графа многовариантного операционного маршрута

Граф, изображенный на рис.2.1, может отображать, к примеру, следующее:

-различные концентрации технологических операций: операция, соответствующая вершине 8, включает в себя переходы операций, соответствующих вершинам 2 и 3; операция, соответствующая вершине 7 включает операции 2 и 3 вершин; операция, соответствующая вершине 10 включает операции 3, 4, 5 вершин);

-использование альтернативных операций например, за счет применения технологического оборудования с различной степенью автоматизации либо различных методов обработки (например, сверление или электроэрозионная обработка): на графе это операции, соответствующие вершинам 7 и 8;

Основной целью системного анализа технологического процесса на операционном уровне является выбор оптимального маршрута: такого пути на многовариантном графе, который является наилучшим по выбранным заранее критериям. Рассмотрим подробнее процесс выбора оптимального пути (варианта технологического процесса).

Основными критериями оптимизации могут быть: приведенные затраты на операцию, штучное (штучно-калькуляционное) время и др. В качестве дополнительных критериев оптимизации могут служить площадь, занимаемая оборудованием, энергоемкость и др.

Существует ряд методов решения многокритериальных оптимизационных задач, наиболее используемыми являются:

- построение обобщенного критерия оптимизации;

- пороговая оптимизация.

Оптимизация по обобщенному критерию

Суть данной процедуры сводится к следующему: вершинам графа (которые обозначают технологические операции) при нормировании ставится в соответствие величина обобщенного критерия оптимизации, который определяется по формуле

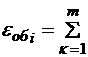
(2.1)

где – весовой коэффициент, определяющий значение -го критерия и назначаемый экспертно; - значение -го критерия для i-й вершины графа, приведенного к относительному виду.

Причем, должно выполняться условие

; (2.2)

Величина определяется по формуле

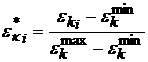
, (2.3)

где , - соответственно минимальное и максимальное значения, которое принимает k-й критерий оптимизации на всех n вершинах графа. Из зависимости (2.3) видно, что .

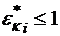К примеру, если каждой i-й вершине графа приписаны три критерия оптимизации - себестоимость обработки , штучное время , площадь под оборудованием , то зависимость (1.1) в этом случае будет иметь вид:

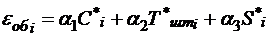(2.4)

Весовые коэффициенты 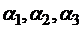назначаются исходя из важности того или иного критерия с учетом соотношения (2.2).

Пороговая оптимизация

На множестве всех возможных путей графа q, соединяющих первую вершину с последней, определим понятие j-й длины пути (j=1,q) по k-му критерию оптимизации : это сумма значений k-го критерия по всем вершинам j-го пути.

Пороговая оптимизация выполняется в виде следующих шагов.

1) Назначают главный и множество второстепенных критериев оптимизации , k=1,m-1 и присваивают их каждой вершине графа (операции): ,, k=1,m-1.

2)Определяем множество , j=1,q, k=1,m с помощью программы AMACONT, выбрав в качестве основного критерия - критерий . В результате получается полный перечень путей графа, отсортированный в порядке возрастания основного критерия .

3) Для каждого k-го второстепенного критерия экспертно назначается ограничение (порог) на длину пути .

4) Пороговое значение отсекает часть множества q всех путей графа: путь отсекается – вычеркивается из перечня, полученного в п.2, если хотя бы по одному из второстепенных критериев оптимизации он не удовлетворяет неравенству - если оптимизация k-го критерия предусматривает его минимизацию и неравенству если оптимизация k-го критерия предусматривает его максимизацию.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4