Лабораторный практикум по дисциплине «Системный анализ и математическое моделирование процессов в машиностроении» (стр. 3 )

По каждому заданию необходимо:

1) записать систему ограничений задачи и выражение для целевой функции;

2) записать результаты решения: искомые параметры (с расшифровкой полученных числовых величин), экстремальное значение целевой функции;

3) скопировать соответствующие результаты решения из MS Excel в отчет по лабораторной работе

3.5.СОДЕРЖАНИЕ ОТЧЕТА

Отчет выполнить в письменном виде на формате А4. Отчет должен включать:

1) краткие теоретические сведения;

2) задание;

3) аналитические зависимости: систему ограничений и целевую функцию;

4) распечатку результатов расчета неизвестных параметров;

5) результаты расчета в расшифрованном виде.

3.6. КОНТРОЛЬНЫЕ ВОПРОСЫ

1) Какие технические задачи решаются в математическом программировании?

2) Какие технологические задачи решаются в математическом программировании?

3) Какие технико-экономические задачи решаются в математическом программировании?

4) Что входит в систему ограничений задачи линейного программирования при расцеховке изделий?

5) Что оптимизируется в задаче расцеховки изделий?

СПИСОК ЛИТЕРАТУРЫ

1. , Бакусова моделирование в машиностроении на основе линейного программирования: учебное пособие по дисциплине «Системный анализ и математическон моделирование процессов в машиностроении» / , ; Уфимск. гос. авиац. ун-т – Уфа, 20с.

2. Акулич программирование в примерах и задачах.. М.: Высшая школа, 19с.

3. Решение задачи расцеховки изделий с использованием линейного программирования: методические указания / сост. ёров, . Уфа: УГАТУ, 19с.

4. Бережная, Е. В., Бережной, методы моделирования экономических систем: учеб. пособие / , . М.: Финансы и статистика, 20с.

5. Долголаптев, в Excel 7.0 для Windows 95 на примерах / . М.: БИНОМ, 19с.

6. , Давлеткулов задачи расцеховки изделий методом линейного прогрмирования: Методические указания к лабораторной работе по дисциплине «Математическое моделирование в машиностроении» / Уфимск. гос. авиац. техн. ун-т, Уфа, 1996. – 10 с.

ПРИЛОЖЕНИЕ

РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

В MS Excel

Активизировать решение задач математического программирования можно с помощью инструмента Поиск решения. Для запуска этого инструмента выполните команду Сервис / Надстройки. Появится окно диалога «Надстройки», в котором установите флажок на строке Поиск решения и нажмите кнопку ОК

После загрузки инструмента Поиск решения в списке опций ниспадающего меню Сервис появится новая команда Поиск решения. В результате выполнения этой команды появляется окно диалога «Поиск решения».

В поле ввода Установить целевую ячейку указывается ссылка на ячейку с целевой функцией, значение которой будет максимальным, минимальным или нулем в зависимости от выбранного вами переключателя.

В поле ввода Изменяя ячейки указываются ячейки, которые отведены под переменные целевой функции.

Кнопка Параметры вызывает окно диалога «Параметры поиска решения», в котором вы можете изменять параметры алгоритма поиска решения.

Для примера определим оптимальный план выпуска продукции в условиях дефицита сырья. Предположим, что предприятие выпускает два вида продукции. Цена единицы 1 вида продукции равна 25000 руб., 2 вида – 50 000 руб.

Для изготовления продукции используются три вида сырья, запасы которого оцениваются в 37, 57,6 и 7 условных единиц. Соответствующие коэффициенты приведены в табл. П1.

Таблица П1

Коэффициенты расхода сырья на единицу продукции

Обозначим количество произведенной продукции 1 вида через С1, 2 вида – С2. Целевая функция есть выражение следующего вида:

J (C1,C2) = 25000*C1 + 50000*C2

Это есть цена произведенной продукции. Наше решение должно обеспечить максимальное значение этой функции.

Табл. П1 налагает на величины С1 и С2 ограничения следующего вида:

1,2*С1 + 1,9*С2 ≤ 37

2,3*С1 + 1,8*С2 ≤ 57,6

0,1*С1 + 0,7*С2 ≤ 7

С1 ≥ 0

С2 ≥ 0

Задача поставлена и приступаем к ее решению. Выполните следующие действия:

1. Введите в ячейки С1 и С2 начальные значения переменных. В нашем случае положим эти значения нулевыми.

2. Введите в ячейку А1 формулу для целевой функции: =25000*С1 + + 50000*С2

(для ввода С1 и С2 нужно щелкнуть на соответствующей ячейке, т. е. создать

ссылку).

3. Введите в ячейку А3 формулу для ограничения: =1,2*С1+1,9*С2.

4. Введите в ячейку А4 формулу для ограничения: =2,3*С1+1,8*С2

5. Введите в ячейку А5 формулу для ограничения: =0,1*С1+0,7*С2

6. Введите в ячейку А6 формулу для ограничения: =С1

7. Введите в ячейку А7 формулу для ограничения: =С2.

8. Выполните команду Сервис / Поиск решения. Появится окно диалога «Поиск решения»

9. В поле ввода Установить целевую ячейку введите ссылку на ячейку А1.

10. В поле ввода Изменяя ячейки укажите ссылки на ячейки С1:С2.

11. Начинаем вводить информацию в поле ввода Ограничения. Нажмите кнопку Добавить. Появится окно диалога Добавить ограничения. В поле ввода Ссылка на ячейку введите ссылку на ячейку А3. В поле ввода Ограничение введите ≤ и число 37.

12. Воспользуйтесь кнопкой Добавить для ввода остальных ограничений. Для изменения ограничения установите на него курсор и нажмите кнопку Изменить.

13. Аналогичную операцию проделайте для ввода ограничения на целочисленность переменных. В поле ввода Ссылка на ячейку введите ссылку на ячейку А6. В поле ввода Ограничение введите цел. Аналогично – для ячейки А7.

14. Нажмите кнопку Выполнить. После окончания расчета Excel откроет окно диалога «Результаты поиска решения».

15. Выберите в окне «Тип отчета» Результаты и нажмите кнопку ОК. Перед тем листом, где записана постановка задачи, будет вставлен лист «Отчет по результатам 1», а на экране вы увидите ответ на поставленную задачу. В ячейках С1 и С2 отображаются значения переменных, на которых достигается максимальное значение целевой функции.

16. Нажмите мышью ярлык Отчет по результатам. На экране появится отчет Excel о решенной задаче.

ЛАБОРАТОРНАЯ РАБОТА №4

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

ФУНКЦИОНИРОВАНИЯ ГПС

4.1. ЦЕЛИ РАБОТЫ

Целями работы является:

- ознакомление студентов с принципами моделирования ГПС на основе теории массового обслуживания;

- привитие студентам навыков определения основных параметров функционирования ГПС.

- расчет параметров работы ГПС на основе математического моделирования ее функционирования с использованием теории массового обслуживания.

4.2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Современные металлообрабатывающие станки и многооперационные обрабатывающие центры оснащены ЧПУ. При этом возникают задачи управления работой не только металлообрабатывающими станками, но и всем циклом технологического процесса начиная с проектирования до изготовления готовых изделий, в том числе и координацией взаимодействия элементов, входящих в ГПС. При этом заданные технологические параметры генерируются в управляющие технологические программы и передаются по каналам связи в систему ЧПУ станка и другие системы, например, систему управления роботов по обслуживанию складов или систему доставки детали в центр сборки по конвейеру и т. д.

Теория массового обслуживания является базой для расчета параметров работы гибких производственных систем (ГПС). В результате расчетов определяются параметры надежности работы ГПС лаборатории «Компьютерное интегрированное производство», входящей в состав Технопарка авиационных технологий (созданного совместно УГАТУ и ).

4.2.1. Сведения о ГПС Технопарка авиационных технологий

ГПС лаборатории «Компьютерное интегрированное производство», входящей в состав Технопарка авиационных технологий был создан для учебных целей: для обучения студентов УГАТУ и работников УМПО. На этой ГПС возможно проводить широкий комплекс работ по разработке, изучению и моделированию автоматизированных производств. Возможно воздействие на работу ГПС как в материальном виде, так и в виртуальном, моделируя все воздействия на компьютере и наблюдая за работой виртуальной ГПС на мониторе. Использование компьютерных технологий позволяет реализовать различные проектные решения.

Возможно также определение оптимального состава и конфигурации ГПС, а также оптимального потока поступления заготовок в зону обработки и ряд других характеристик.

Общий вид (схема) ГПС представлен на рис. 4.1.

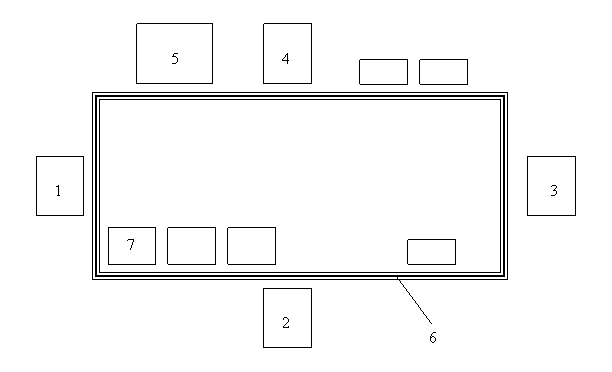
Рис. 4.1 – Схема ГПС «CIM System»:

1 - Мини склад, робот по обслуживанию склада

2 – Рабочий стол с приставкой для компьютера

3 – Фрезерный обрабатывающий центр с ЧПУ 5000 RPM 220 V, робот по обслуживанию обрабатывающего центра 5000 RPM 200V

4 - Робот сборки и контроля качества с машинным зрением

5 – Установка для электродуговой сварки в рабочей камере

6 - Пластинчатый конвейер замкнутого контура, размер 2040мм x 1400мм

7 - Палета размером 200х150 мм

4.2.2. Расчет основных показателей работы ГПС на основе теории массового обслуживания

В рассматриваемой работе на основе теоретических моделей массового обслуживания предусмотрено проведение расчетов характеристик надежности работы ГПС, интенсивности поступления деталей на транспортер ГПС в зависимости от заданной вероятности отказа в обслуживании.

Теория массового обслуживания занимается вопросами образования очередей, обслуживанием заявок – однотипных требований, которые поступают с систему в массовом количестве. Обслуживание происходит прибором (терминология ТМО), который расположен на канале обслуживания. Приборов и соответствующих каналов обслуживания может быть несколько. Существует ряд разновидностей моделей: с неограниченной очередью, с ограничением длины очереди, с отказом в обслуживании (при занятом канале), с приоритетом и др. Поток заявок подчиняется распределению Пуассона...

Система массового обслуживания может быть описана графом состояний. Состояния системы изображаются прямоугольниками, а возможные переходы – стрелками.

Рассмотрим пример случайного процесса: техническое устройство состоит из двух узлов, каждый из которых в случайный момент времени может отказать. После чего мгновенно начинается ремонт узла, тоже продолжающийся случайное время. Возможные состояния системы:

- оба узла исправны

- 1-й узел ремонтируется, второй исправен

- 2-й узел ремонтируется, первый исправен

- оба узла ремонтируются.

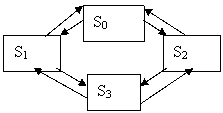Рис. 4.2. Граф состояний

В зависимости от типов моделей графы состояний системы будут различными.

Рассмотрим многоканальную систему с отказами. В качестве примера рассмотрим станочную систему, состоящую из параллельно работающих единиц оборудования и оснащенную центральным накопителем емкости на мест. В накопитель поштучно поступают заготовки с интенсивностью . Каждая поступившая в систему заготовка доступна для обработки, если в ней имеется хотя бы один свободный станок, в противном случае заготовки ожидают своей очереди обработки в накопителе. Интенсивность обработки , где -средняя длительность обработки. Рассматриваемая система является многокритериальной СМО с ограниченной очередью.

Рассмотрим возможные состояния системы : - все станки и накопитель свободны; - занят один станок, остальные станки и накопитель свободны; - заняты все станки, накопитель свободен; - заняты все станки и одно место в накопителе; - заняты все станки и все места в накопителе.

Таким образом, состояние системы определяется числом находящихся в ней заготовок (требований).

Увеличение числа занятых станков и мест в накопителе, переход из состояния в состояние происходит под действием входного потока заготовок с интенсивностью . Пропускная способность одновременно работающих станков суммируется, поэтому переход из состояния в состояние определяет поток событий с интенсивностью , если и , если . На рисунке показан граф состояний рассматриваемой системы.

Граф состояний системы изображен на рис. 4.3.

Рис. 4.3. Граф состояний системы

Обозначим через вероятность того, что система находится в состоянии . Принимая, что число уходов и приходов в каждое из возможных состояний будет сбалансированным, граф состояния можно описать следующей системой уравнений Колмогорова:

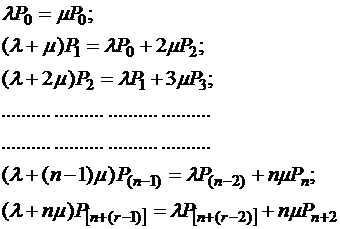
Поскольку система с достоверностью может находиться в любой из возможных состояний, то 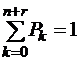. Решая систему уравнений и вводя обозначения 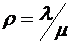, определяем вероятность того, что занято k каналов обслуживания (станков и мест в накопителе) по формуле

при 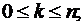(4.1)

при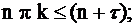

Вероятность, что все каналы обслуживания свободны (все станки и места в накопителе свободны) определяется по формуле

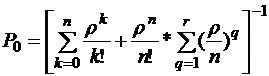(4.2)

Поступающие в систему заготовки получают отказ, если заняты все станки и накопитель, т. е. при 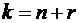. Вероятность отказа равна

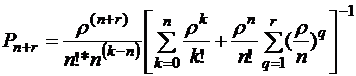(4.3)

Число станков, занятых обработкой, вытекает из состояния . Среднее число занятых станков в установившемся процессе обработки деталей равно

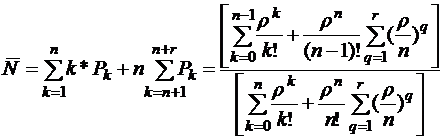
(4.4)

Если в момент поступления заготовки все станки заняты и, кроме того, уже имеется очередь в накопителе из заготовок, то средняя длительность ожидания обработки равна

.

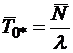Приведенная методика анализа и полученные общие зависимости могут быть использованы и для решения других частных задач. При имеет место одноканальная СМО с очередью (например, станок с локальным накопителем) при будем рассматривать - канальную систему с отказами.

4.3. ЗАДАНИЕ

Задание на лабораторную работу состоит из 2-х частей и выполняется по вариантам. Принята модель системы с отказами, состоящая из станков с общим накопителем объемом r.

Задание1. Рассчитать вероятности состояний ГПС при заданных параметрах работы (для всех вариантов):

- средняя интенсивность поступления заготовок на обработку со склада =4,

- среднее время обработки заготовки =3,

- количество станков =4,

- количество мест в накопителе (общем для всей ГПС) r=4.

Варианты задания приведены в таблице 4.1.

Таблица 4.1.

Варианты задания 1

Задание 2. Рассчитать среднюю интенсивность поступления заготовок на обработку со склада по следующим исходным данным

Таблица 4.2.

Варианты задания 2

4.4. МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4