Неравенства могут быть строгими – в том случае, если длина пути, равная пороговой не включается в множество путей, прошедших порог.
5)Таким образом множество всех путей q проверяется на соответствие ограничениям по каждому из второстепенных критериев. Остаются лишь те пути, которые удовлетворяют всем ограничениям, т. е. прошли пороги по всем второстепенным критериям. Обозначим это множество ![]() .
.
6)На множестве ![]() проводим однокритериальную оптимизацию по программе AMACONT, т. е. из множества путей
проводим однокритериальную оптимизацию по программе AMACONT, т. е. из множества путей ![]() выбираем тот, который содержит наилучший показатель основного (главного) критерия (к примеру, если это себестоимость С, то минимальное значение)
выбираем тот, который содержит наилучший показатель основного (главного) критерия (к примеру, если это себестоимость С, то минимальное значение)
2.3. ЗАДАНИЕ
Преподавателем выдается индивидуальное задание – многовариантный граф операций технологического процесса, где каждой вершине поставлено в соответствие значение двух безразмерных критериев оптимизации (условно, 1-го и 2-го).
В задании необходимо выполнить следующие оптимизационные расчеты, используя AMACONT (по выданному варианту задания):
1) Однокритериальную оптимизацию:
- по первому критерию;
- по второму критерию
2)Многокритериальную оптимизацию:
- по обобщенному критерию, приняв ![]() = 0,6 и
= 0,6 и ![]() =0,4;
=0,4;
- пороговую, приняв в качестве основного – 1-й критерий, пороговые значения 2-го критерия (второстепенного) указаны в варианте задания.
2.4. МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ
Данные для оптимизационных расчетов вводятся либо с клавиатуры, либо из файла.
При вводе с клавиатуры программа работает в диалоговом режиме, запрашивая последовательный ввод ребер графа, количества и значений критериев оптимизации по каждой вершине.
Автоматически программа считает, что оптимальное значение – минимум. В ином случае, необходимо вводить данные, добавив к ним минус.
При вводе из файла, его необходимо создать с расширением txt. Т. е. в «Блокноте». Порядок ввода таков: в первой строке вводятся значения вершин, соответствующие ребрам графа (через пробелы): пары номеров вершин, соответствующие «вершинам-предкам» и «вершинам-потомкам» для каждого ребра. На следующей строке указывается знак # и указывается количество критериев оптимизации. Со следующей строки указываются значения критериев оптимизации по каждой вершине от первой до последней – каждая вершина на отдельной строке (см. пример заполнения файла исходных данных)
Требования к составлению графа (является специфическим условием работы программы AMACONT):
1) Ребра соединяют лишь вершины соседних слоев
2) Ребра не соединяют вершины внутри слоя (в ином случае необходимо преобразовать граф, добавив фиктивные вершины)
3) Ребра не соединяют вершины через слой (в ином случае необходимо преобразовать граф, добавив фиктивные вершины)
4) Граф должен начинаться с одной вершины и заканчиваться одной вершиной (в ином случае необходимо добавить фиктивные вершины начала и (или) конца графа)
5) Нумерации вершин и ребер должны быть строго по слоям – от первого до последнего, в каждом слое сверху вниз).
Когда указывается, какой критерий основной, результаты расчета сортируются таким образом, что первая строка соответствует минимальному пути по основному критерию и далее в порядке возрастания основного критерия. При этом длина пути по основному критерию подсвечивается красным.
2.5. СОДЕРЖАНИЕ ОТЧЕТА
Отчет по лабораторной работе должен содержать:
1) цель работы;
2) вариант задания, в т. ч. граф;
3) распечатки вводимых файлов;
4) распечатки оптимизационных расчетов;
5) результаты оптимизационных расчетов;
6) выводы по результатам расчетов.
2.6. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Каков порядок пороговой оптимизации?
2. Что такое весовой коэффициент?
3. Почему необходимо при расчете по обобщенному критерию приводить значения критериев к безразмерному виду?
4. В чем достоинства и недостатки оптимизации по обобщенному критерию и пороговой оптимизации
5. Какие критерии могут быть выбраны в качестве критериев оптимизации?
СПИСОК ЛИТЕРАТУРЫ
1. «Системный анализ и математическое моделирование процессов в машиностроении»: учебное пособие / ; Уфимск. гос. авиац. техн. ун-т.- Уфа, 20с.
2. А. и др. Структурная оптимизация технологических процессов в машиностроении: Учебное пособие / , . - Уфа: Гилем, 19с.
3.Анферов и. оптимизация структуры технологических процессов: Учебное пособие / - Уфа: УГАТУ, 19с.
ЛАБОРАТОРНАЯ РАБОТА №3
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
В МАШИНОСТРОЕНИИ
НА ОСНОВЕ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
3.1. ЦЕЛЬ РАБОТЫ
Освоить математическое программирование, выполнив конкретное задание по определению программ выпуска изделий, по «расцеховке» изделий и по рациональному раскрою листового материала. Научиться выполнять решения задач математического программирования в среде MS Excel
3.2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Методы математического программирования представляют собой класс моделей, применяемых для формализации задач планирования, предусматривающих распределение ограниченного количества ресурсов разных видов. Подобного рода задачи решаются в различных отраслях деятельности: в экономике, в промышленности, при разработке проектов, составлении расписаний, планировании военных операций и т. п.
Употребление слова «программирование» связано с тем, что при решении задач находят такой набор переменных, который является программой (планом) при выполнении поставленной задачи. Методы линейного программирования применяются в случае, когда математическая модель изучаемого процесса может быть представлена в виде совокупности линейных отношений. Эти линейные отношения связывают некоторые параметры, определяющие ход процесса, и состоят из системы ограничений и целевой функции.
Методы решения такого типа задач позволяют найти оптимальные варианты управления, процессы, структуры, т. е. выбрать лучшее решение из всех возможных. Такие задачи относятся к задачам оптимизации.
Условно типы задач из области машиностроения можно разделить на технико-экономические, технические, технологические, проектно-организационные, транспортные. Косвенным образом соотносятся с машиностроением и другие типы задач, которые могут быть решены методом линейного программирования: задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарное планировании, межотраслевого баланса и т. п.
В рассматриваемой лабораторной работе требуется составить математическую модель задачи машиностроения, основанной на линейном программировании. Требуется составить целевую функцию, систему ограничений и решить задачу, пользуясь MS EXCEL.
3.2.1.Технико-экономическая задача определения программ выпуска нескольких видов продукции при ограниченности
сырья
Рассмотрим постановку этой задачи на конкретном примере.
Для изготовления двух видов продукции ![]() используют три вида сырья:
используют три вида сырья: ![]() Запасы сырья, затрачиваемые на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции приведены в табл. 2.1. Необходимо составить такой план выпуска продукции, чтобы при её реализации получить максимальную прибыль.
Запасы сырья, затрачиваемые на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции приведены в табл. 2.1. Необходимо составить такой план выпуска продукции, чтобы при её реализации получить максимальную прибыль.
Таблица 3.1
Исходные данные
Вид сырья | Запасы сырья | Кол-во единиц сырья, идущих на изготовление единицы продукции | |
|
| ||
| 20 | 2 | 5 |
| 40 | 8 | 5 |
| 30 | 5 | 6 |
Прибыль от единицы продукции, руб. | 50 | 40 |
Обозначим через ![]() количество единиц продукции
количество единиц продукции ![]() , а через
, а через ![]() количество единиц продукции
количество единиц продукции ![]() . Тогда, учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим систему ограничений:
. Тогда, учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим систему ограничений:
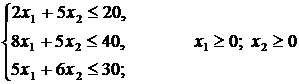 , (3.1)
, (3.1)
которая показывает, что количество сырья, необходимое на изготовление продукции, не может превысить имеющихся запасов. Кроме того, на неизвестные ![]() и
и ![]() должно быть наложено ограничение неотрицательности:
должно быть наложено ограничение неотрицательности: ![]() (с позиций здравого смысла)
(с позиций здравого смысла)
Конечную цель решаемой задачи – получение максимальной прибыли при реализации продукции – выразим как функцию двух переменных ![]() и
и ![]() . Реализация
. Реализация ![]() единиц продукции вида
единиц продукции вида ![]() и
и ![]() единиц продукции вида
единиц продукции вида ![]() дает соответственно
дает соответственно ![]() и
и ![]() руб. прибыли. Выражение для суммарной прибыли есть также выражение для целевой функции задачи
руб. прибыли. Выражение для суммарной прибыли есть также выражение для целевой функции задачи
![]() . (3.2)
. (3.2)
Необходимо найти такие неотрицательные значения ![]() и
и ![]() , которые удовлетворяли бы системе ограничений (3.1) и при которых функция (3.2) мела бы максимальное значение.
, которые удовлетворяли бы системе ограничений (3.1) и при которых функция (3.2) мела бы максимальное значение.
3.2.2. Техническая задача определения рационального способа разрезки (раскроя) листового материала
Также рассмотрим на конкретном примере.
На предприятии из стандартных листов стального проката необходимо вырезать заготовки трех видов в количествах, соответственно равных 24, 31 и 18 шт. Каждый лист может быть разрезан на заготовки двумя способами. Количество получаемых заготовок при данном способе раскроя приведено в табл. 2.2. В ней же указана величина отходов, которые получаются при данном способе раскроя одного листа стального проката.
Таблица 3.2
Исходные данные к задаче определения рационального способа разрезки листового материала
Вид заготовки | Количество заготовок (шт.) при раскрое по способу | |
1 | 2 | |
I | 2 | 6 |
II | 5 | 4 |
III | 2 | 3 |
Величина отходов (см 2) | 12 | 16 |
Определить, сколько листов проката и по какому способу следует раскроить так, чтобы было получено не меньше нужного количества заготовок при минимальных отходах.
3.2.3. Организационно-техническая задача распределения различных изделий для изготовления в различных цехах
(«расцеховка») либо распределение по участкам цеха,
либо распределение по рабочим местам (оборудованию)
При разработке межцехового технологического маршрута необходимо провести так называемую расцеховку деталей (изделий): распределить множество групп деталей  между группой цехов C={ci}. Заданы: суммарная трудоемкость
между группой цехов C={ci}. Заданы: суммарная трудоемкость ![]() изготовления детали-представителя i-й группы.
изготовления детали-представителя i-й группы.
Найти xij – количество деталей i-й группы (часть от программы ![]() ), обработка которых должна производиться в j-м цехе. На рис. 3.1 показан двудольный граф соответствий элементов множеств D и C.
), обработка которых должна производиться в j-м цехе. На рис. 3.1 показан двудольный граф соответствий элементов множеств D и C.
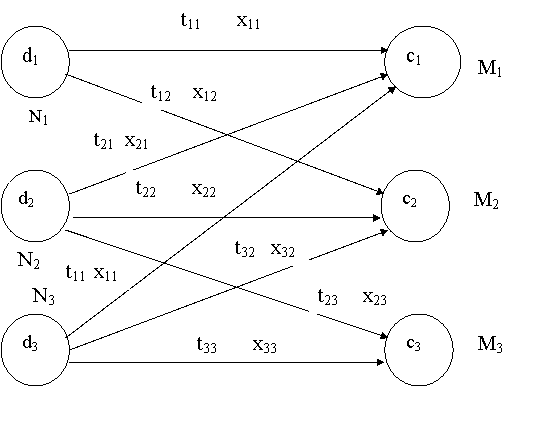

Рис. 3.1. Двудольный граф соответствий элементов множеств D и C:
![]() - программа выпуска i-й детали,
- программа выпуска i-й детали, ![]() - мощность j-го цеха в нормо-часах
- мощность j-го цеха в нормо-часах
Для решения задачи составляются системы линейных уравнений:
1. Баланс мощностей цехов ![]()
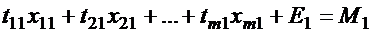 ;
;
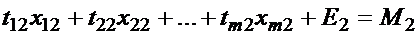 ; (3.3)
; (3.3)
……………………………
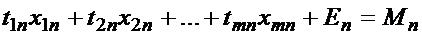 .
.
Мощность цеха ![]() задается в нормо-часах и определяется суммарным временем работы оборудования цеха за определенный период времени (в рассматриваемом случае – за год).
задается в нормо-часах и определяется суммарным временем работы оборудования цеха за определенный период времени (в рассматриваемом случае – за год).
![]() - резерв мощности i – го цеха, показывает недоиспользованную мощность цеха при выбранном варианте распределения деталей.
- резерв мощности i – го цеха, показывает недоиспользованную мощность цеха при выбранном варианте распределения деталей.
2. Баланс расчетных программ групп деталей ![]()
![]() ;
;
![]() ; (3.4)
; (3.4)
………………….
![]()
3. Равномерность относительной загрузки цехов
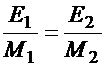 ;
;
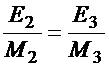 ; (3.5)
; (3.5)
…………
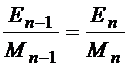 ,
,
где ![]() – мощность
– мощность ![]() -го цеха;
-го цеха; ![]() – резерв мощности
– резерв мощности ![]() -го цеха.
-го цеха.
Целевая функция, которую необходимо максимизировать, записывается в виде
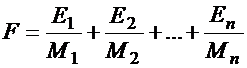 . (3.6)
. (3.6)
Эта функция выражает стремление минимизировать время обработки деталей в каждом цехе (относительный резерв мощности при этом должен увеличиваться)
3.3. ЗАДАНИЕ
Работа включает три задания:
1) определить программы выпуска нескольких видов продукции при ограниченности сырья (см. п. 1.1);
2) определить рациональный способ разрезки (раскроя) листового материала (см. п. 1.2);
3) распределить различные изделия для изготовления в различных цехах («расцеховка») (см. п. 1.3).
По каждому заданию преподаватель выдает каждому студенту (или 2-м, 3-м студентам, работающим за одним компьютером) индивидуальный вариант.
Примеры заданий.
К заданию 1:
Вид сырья | Запасы сырья | Кол-во единиц сырья, идущих на изготовление единицы продукции | |
|
| ||
| 25 | 3 | 4 |
| 35 | 5 | 5 |
| 40 | 4 | 3 |
| 20 | 3 | 4 |
Прибыль от единицы продукции, руб. | 40 | 45 |
К заданию 2:
Вид заготовки | Количество заготовок (шт.) при раскрое по способу | |
I | II | |
I | 3 | 5 |
II | 4 | 5 |
III | 3 | 6 |
Величина отходов (см 2) | 10 | 9 |
К заданию 3:
Программы | Мощности цехов, нормо-часы | ||
200 | 300 | 400 | |
Трудоемкость, час | |||
20 | 3 | 2 | 1 |
30 | 0 | 3 | 2 |
40 | 0 | 0 | 4 |
50 | 5 | 0 | 3 |
3.4. МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 |





