4.2 Истечение под уровень

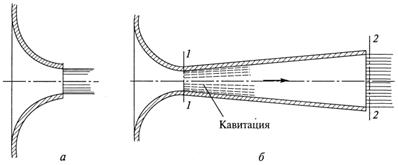
При течении жидкости в закрытых руслах часто приходится иметь дело с истечением жидкости не в газовую среду, а в пространство, заполненное этой же жидкостью (рисунок 4.2). Такое истечение называется истечением под уровень, или истечением через затопленное отверстие.

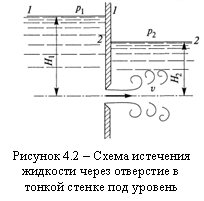Здесь, так же как и в предыдущем случае, при определении расхода Q следует составить уравнение Бернулли. Запишем его для сечений 1–1 и 2–2, в которых скорости движения жидкости принимаются равными нулю:

,

где – потери напора при движении жидкости между сечениями 1–1 и 2–2.

При определении потерь на-пора в этом случае необходимо учитывать, что они складываются из двух составляющих:

,

где ho – потери напора на торможение частиц жидкости о входную кромку отверстия;

hв. р – потери напора на внезапное расширение в баке после прохождения жидкости через отверстие.

Потери ho практически равны потерям при истечении через отверстие в газовую среду:

.

Следует иметь в виду, что при истечении под уровень вся кинетическая энергия струи, приобретенная частицами жидкости в от­верстии, при попадании в покоящуюся жидкость теряется на вихреобразование так же, как при внезапном расширении. Поэтому потери hв. р численно равны соответствующему скоростному напору, посчитанному по средней скорости жидкости в струе с учетом коэффициента Кориолиса α:

.

Таким образом, суммарные потери напора

.

Подставив полученное выражение в уравнение Бернулли, получим

.

Если в этом уравнении за расчетный напор принять выражение , то после преобразований можно получить формулу, определяющую значение средней скорости жидкости в сжатом сечении струи:

,

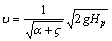которая совпадает с формулой (4.2). Это значит, что, проводя дальнейшие преобразования, необходимые для получения формулы, определяющей расход Q при истечении, можно получить формулы (4.6)
и (4.7).

Таким образом, как при истечении в газовую среду, так и при истечении под уровень расчетные формулы, определяющие расход Q, имеют один и тот же вид. Кроме того, как показала практика, коэффициенты , и , использующиеся в этих формулах, в обоих случаях истечения имеют одинаковые значения при равенстве соответствующих чисел Рейнольдса.

4.3 Истечение через насадки

Анализ полученных формул (4.6) и (4.7) позволяет заключить, что увеличение расхода Q при истечении через отверстие с неизменными значениями So и Hр возможно при увеличении коэффициента расхода . Для решения этой задачи служат насадки различной конструкции. Различают следующие типы насадков: цилиндрические (внешний
и внутренний), конические (сходящийся и расходящийся), коноидальные и комбинированные.

Внешним цилиндрическим насадком называется короткая трубка или просверленное отверстие в толстой стенке без обработки входной кромки (рисунок 4.3). Его длина l = (3…5) d, где d – диаметр отверстия.

На практике при истечении в газовую среду можно наблюдать два режима истечения жидкости через цилиндрический насадок: безотрывный (см. рисунок 4.3а) и с отрывом потока от стенок (см. рисунок 4.3б).

Безотрывный режим истечения характеризуется тем, что внутри насадка поток жидкости вначале сжимается до некоторого минимального поперечного сечения, площадь которого можно опре­делить по значению коэффициента сжатия струи , взятого для случая истечения жидкости через отверстие в тонкой стенке, а затем расширяется до размеров отверстия в насадке. В итоге при таком режиме истечения из насадка на его выходе сжатие струи отсутствует ( = 1) и площадь сечения струи равна площади проходного сечения отверстия в насадке. Поэтому в данном случае при определении расхода Q по формуле (4.7) коэффициент расхода = .

Для этого случая при турбулентном режиме течения жидкости внутри насадка (α = 1) и коэффициенте потерь = 0,5 (потери напора определяются как потери при внезапном сужении) коэффициент расхода

.

Сравнение полученных коэффициентов скорости и расхода со значениями этих ко­эффициентов при истечении жидкости через отверстие в тонкой стенке ( = 0,97, = 0,62) показывает, что при безотрывном истечении через цилиндрический насадок расход Q полу-чается больше, чем при истечении через такое же отверстие в тонкой стенке. Средняя скорость жидкости в потоке на выходе из насадка

при этом получается меньше. Уменьшение скорости вызвано большими

потерями напора в насадке по сравнению с потерями, которые возникают на входной кромке отверстия в тонкой стенке.

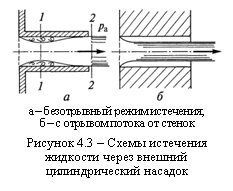Увеличение расхода Q при этом является следствием отсутствия сжатия струи на выходе из насадка. Кроме того, при безотрывном истечении на входе в насадок поток сжимается, а значит,

в соответствии с законом Бернулли скорость движения жидкости увеличивается, а давление
в этом месте уменьшается по сравнению с давлением среды, куда происходит истечение. Причем степень сжатия потока, а следовательно,
и степень уменьшения давления в узком сечении потока тем больше, чем больше расчетный напор Hр. При этом на входной кромке отверстия создается больший перепад давления, чем при истечении жидкости через отверстие в тонкой стенке при одном и том же значении Hр. В результате этого обеспечиваются дополнительный приток жидкости из бака в насадок и увеличение расхода Q.

Со сжатием потока на входе в насадок, а также с зависимостью степени сжатия от расчетного напора Нр связано внезапное изменение режима истечения через насадок. Это происходит при определенном критическом расчетном напоре Hкр, который при истечении воды
в атмосферу составляет около 14 м водяного столба. Внешне эта смена режима истечения заключается в том, что поток жидкости отрывается от стенок насадка, и жидкость истекает в атмосферу, не касаясь их. Этот режим истечения получил название истечение с отрывом потока от стенок насадка (см. рисунок 4.3б).

При истечении до отрыва потока от стенок давление в узком сечении потока приближается к давлению насыщенных паров. Как известно, в потоке при таком давлении следует ожидать возникновения

кавитации. Однако кавитационный режим течения при истечении
в газовую среду не успевает сформироваться. Возникающая начальная стадия кавитации способствует проникновению газовой среды внутрь насадка. Начиная с этого момента, струя жидкости после сжатия теряет взаимодействие со стенками насадка и уже не расширяется, а перемещается внутри насадка, не соприкасаясь с его стенками. Истечение становится таким же, как и при истечении через отверстие в тонкой стенке (см. 4.1), с теми же значениями коэффициентов , и . Таким образом, при смене режима истечения происходит скачкообразное уменьшение расхода приблизительно на 20 % за счет существенного сокращения площади сечения потока.

Следует также отметить, что если после отрыва потока от стенок напор Hр начать снижать, то режим истечения с отрывом сохраняется вплоть до самых малых значений напора, пока не произойдет самопроизвольное смачивание внутренней поверхности насадка. Это значит, что режим истечения с отрывом через цилиндрический насадок возможен и при значениях Hр < Hкр. Следовательно, при напоре Hр < Hкр возможны оба режима истечения.

Если жидкость истекает через цилиндрический насадок под уровень, то отрыв потока от стенок не происходит. Начиная с момента, когда в узком сечении потока внутри насадка давление становится близким к давлению насыщенных паров жидкости, на входе в насадок возникает кавитация и происходит связанное с ней увеличение сопротивления насадка.

Итак, использование внешнего цилиндрического насадка вместо отверстия в тонкой стенке обеспечивает в режиме безотрывного истечения при тех же значениях расчетного напора и поперечных размеров отверстия увеличение расхода через насадок.

Однако внешний цилиндрический насадок имеет и недостатки:

- в режиме безотрывного истечения – большое сопротивление и недостаточно высокий коэффициент расхода;

- в режиме истечения с отрывом – низкий коэффициент расхода;

- двойственность режима истечения в газовую среду при Hр < Hкр;

- возможность возникновения кавитации при истечении под уровень.

Это необходимо учитывать при использовании цилиндрического насадка в качестве жиклера, дросселя или форсунки. Улучшить внешний цилиндрический насадок можно за счет скругления входной кромки насадка. Для жиклеров рекомендуется снятие фаски на входе в отверстие с углом конусности около 60°.

Чем больше радиус закругления входной кромки насадка, тем ниже его коэффициент сопротивления и тем выше коэффициент расхода. В пределе, при радиусе кривизны, равном толщине стенки, цилиндрический насадок приближается к коноидальному насадку, или соплу.

Коноидальный насадок (сопло) (рисунок 4.4а) очерчивается по форме естественно сжимающейся струи, поэтому поток жидкости на выходе насадка получается безотрывным, параллельно-струйным
и устойчивым к возникновению кавитации. Для этого насадка коэффициент сжатия струи = 1, а коэффициент = = 0,96...0,99.

Диффузорный насадок (рисунок 4.4б) представляет собой комбинацию сопла и диффузора. Установка диффузора с оптимальным углом на выходе позволяет, не меняя проходного сечения отверстия (сечение 1–1) и расчетного напора, повысить расход жидкости почти в 2,5 раза по сравнению с расходом через сопло. Недостатком диффузорного насадка является склонность его к возникновению кавитации в узком сечении 1–1.

4.4 Истечение жидкости через проходные сечения

в гидравлических устройствах

При определении расхода Q через проходные сечения, образо­ванные взаимным расположением деталей в гидравлических устройствах, кроме оценки коэффициента расхода необходимо, как правило, определять площадь S проходного сечения отверстия как функцию смещения х одной из деталей относительно другой. Обычно величина х и определяет степень открытия проходного сечения.

Для расчетов рекомендуется использовать формулу

,

где S(x) – расчетная площадь проходного сечения, определяемая по значению смещения х перекрывающей детали;

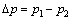– перепад давления на проходном сечении.

Таблица 4.1 – Основные величины, характеризующие истечения

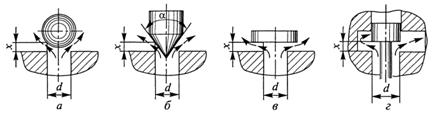
В таблице 4.1 и на рисунке 4.5 приведены основные варианты расчетных схем, полученные в результате анализа наиболее часто встречающихся случаев при решении задач определения расхода.
В основном эти варианты отличаются формой детали, перекрывающей круглое проходное сечение диаметром d, и соотношением поперечных размеров отверстия и перекрывающей детали. Для каждого из них даются рекомендуемые значения коэффициента расхода в области квадратичного сопротивления и формула, позволяющая оценить площадь S(x) соответствующего проходного сечения [3].

5 ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ

5.1 Простой трубопровод постоянного сечения

Трубопровод называется простым, если он не имеет ответвлений. Простые трубопроводы могут образовывать соединения: последовательное, параллельное или разветвленное. Трубопроводы могут быть сложными, содержащими как последовательное, так и параллельное соединения или разветвления.

Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад (разность) уровней энергии может быть создан тем или иным способом: работой насоса, благодаря разности уровней жидкости, давлением газа. В машиностроении приходится иметь дело, главным образом, с трубопроводами, движение жидкости в которых обусловлено работой насоса.

При гидравлическом расчете трубопровода чаще всего определяется его потребный напор Hпотр – величина, численно равная пьезометрической высоте в начальном сечении трубопровода. Если потребный напор задан, то его принято называть располагаемым напором Hрасп.
В этом случае при гидравлическом расчете может определяться расход жидкости Q в трубопроводе или его диаметр d. Значение диаметра трубопровода выбирается из установленного ряда в соответствии
с ГОСТ 16516–80.

Пусть простой трубопровод постоянного проходного сечения, произвольно расположенный в пространстве (рисунок 5.1а), имеет общую длину l и диаметр d и содержит ряд местных гидравлических сопротивлений I и II.

Запишем уравнение Бернулли для начального 1–1 и конечного 2–2 сечений этого трубопровода, считая, что коэффициенты Кориолиса
в этих сечениях одинаковы (α1=α2). После сокращения скоростных напоров получим

,

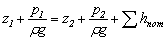где z1, z2 – координаты центров тяжести соответственно начального
и конечного сечений;

p1, p2 – давления в соответственно начальном и конечном сечениях трубопровода;

– суммарные потери напора в трубопроводе.

Отсюда потребный напор

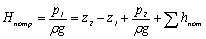. (5.1)

Как видно из полученной формулы, потребный напор складывается из суммарной геометрической высоты Δz = z2 – z1, на которую поднимается жидкость в процессе движения по трубопроводу, пьезометрической высоты в конечном сечении трубопровода и суммы гидравлических потерь напора, возникающих при движении жидкости в нем.

В гидравлике принято под статическим напором трубопровода понимать сумму .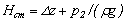

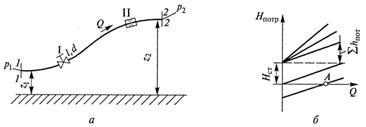
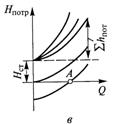
а – расчетная схема; б – характеристики потребного напора при

ламинарном режиме течения; в – то же при турбулентном режиме

Рисунок 5.1 – Простой трубопровод

Тогда, представляя суммарные потери как степенную функцию от расхода Q, получим

, (5.2)

где т – величина, зависящая от режима течения жидкости в трубопроводе;

К – сопротивление трубопровода.

При ламинарном режиме течения жидкости и линейных местных сопротивлениях (заданы их эквивалентные длины lэкв) суммарные потери

,

где lрасч = l + lэкв – расчетная длина трубопровода.

Следовательно, при ламинарном режиме т = 1,

.

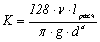При турбулентном течении жидкости

.

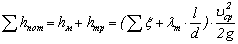Заменяя в этой формуле среднюю скорость жидкости через расход, получим суммарные потери напора

. (5.3)

Тогда при турбулентном режиме ,
а показатель степени m = 2. При этом следует помнить, что в общем случае коэффициент потерь на трение по длине является также функцией расхода Q.

Поступая аналогично в каждом конкретном случае, после несложных алгебраических преобразований и вычислений можно получить формулу, определяющую аналитическую зависимость потребного напора для данного простого трубопровода от расхода в нем. Примеры таких зависимостей в графическом виде приведены на рисунках 5.1б, в.

Анализ формул, приведенных выше, показывает, что решение задачи по определению потребного напора Hпотр при известных расходе Q жидкости в трубопроводе и его диаметре d несложно, так как всегда можно провести оценку режима течения жидкости в трубопроводе, сравнивая критическое значение Reкp = 2300 с его фактическим значением, которое для труб круглого сечения может быть вычислено по формуле

. (5.4)

После определения режима течения можно вычислить потери напора, а затем потребный напор по формуле (5.2).

Если же величины Q или d неизвестны, то в большинстве случаев сложно оценить режим течения, а, следовательно, обоснованно выбрать формулы, определяющие потери напора в трубопроводе. В такой ситуации можно рекомендовать использовать либо метод последовательного приближения, обычно требующий достаточно большого объема вычислительной работы, либо графический метод, при применении которого необходимо строить так называемую характеристику потребного напора трубопровода.

5.2. Построение характеристики потребного напора простого трубопровода

Графическое представление в координатах Н–Q аналитической зависимости (5.2), полученной для данного трубопровода, в гидравлике называется характеристикой потребного напора. На рисунках 5.1б, в приведено несколько возможных характеристик потребного напора (линейные – при ламинарном режиме течения и линейных местных сопротивлениях; криволинейные – при турбулентном режиме течения или наличии в трубопроводе квадратичных местных сопротивлений).

Как видно на графиках, значение статического напора Нст может быть как положительным (жидкость подается на некоторую высоту Δz или в конечном сечении существует избыточное давление p2), так
и отрицательным (при течении жидкости вниз или при ее движении
в полость с разрежением).

Крутизна характеристик потребного напора зависит от сопротивления трубопровода и возрастает с увеличением длины трубы
и уменьшением ее диаметра, а также зависит от количества и характеристик местных гидравлических сопротивлений. Кроме того, при ламинарном режиме течения рассматриваемая величина пропорциональна еще и вязкости жидкости. Точка пересечения характеристики потребного напора с осью абсцисс (точка А на рисунках 5.1б, в) определяет расход жидкости в трубопроводе при движении самотеком.

Графические зависимости потребного напора широко используются для определения расхода Q при расчете как простых трубопроводов, так и сложных [3]. Поэтому рассмотрим методику построения такой зависимости (рисунок 5.2а). Она состоит из следующих этапов.

1-й этап: используя формулу (5.4) определяем значение критического расхода Qкр, соответствующее Reкp=2300, и отмечаем его на оси расходов (ось абсцисс). Очевидно, что для всех расходов, расположенных левее Qкр, в трубопроводе будет ламинарный режим течения, а для расходов, расположенных правее Qкр, – турбулентный.

2-й этап: рассчитываем значения потребного напора Н1 и Н2 при расходе в трубопроводе, равном Qкр, соответственно предполагая, что Н1 – результат расчета при ламинарном режиме течения, а Н2 – при турбулентном.

3-й этап: строим характеристику потребного напора для ламинарного режима течения (для расходов, меньших Qкр). Если местные сопротивления, установленные в трубопроводе, имеют линейную зависимость потерь от расхода, то характеристика потребного напора имеет линейный вид.

4-й этап: строим характеристику потребного напора для турбулентного режима течения (для расходов, больших Qкp). Во всех случаях получается криволинейная характеристика, близкая к параболе второй степени.

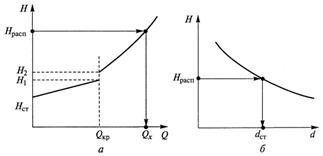
а – кривая потребного напора; б – кривая для определения диаметра

Рисунок 5.2 – Графические зависимости для расчета

простых трубопроводов

Имея характеристику потребного напора для данного трубопровода, можно по известному значению располагаемого напора Hрасп найти искомое значение расхода Qx (см. рисунок 5.2а).

Если же необходимо найти внутренний диаметр трубопровода d, то, задаваясь несколькими значениями d, следует построить зависимость потребного напора Hпотр от диаметра d (рисунок 5.2б). Далее по значению Нрасп выбрать ближайший больший диаметр из стандартного ряда dст.

В ряде случаев на практике при расчете гидросистем вместо характеристики потребного напора используют характеристику трубопровода. Характеристика трубопровода — это зависимость суммарных потерь напора в трубопроводе от расхода. Аналитическое выражение этой зависимости имеет вид

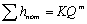. (5.5)

Сравнение формул (5.5) и (5.2) позволяет заключить, что характеристика трубопровода отличается от характеристики потребного напора отсутствием статического напора Hст, а при Hст = 0 эти две зависимости совпадают.

5.3 Соединения простых трубопроводов. Аналитические
и графические способы расчета

Рассмотрим способы расчета соединений простых трубопроводов.

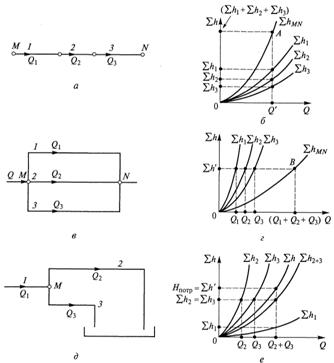
1,2,3 – трубопроводы

Рисунок 5.3 – Схема последовательного (а), параллельного (в) и

сложного (д) соединений трубопроводов и соответствующие им

характеристики (б, г, е)

Пусть имеем последовательное соединение нескольких простых трубопроводов (1, 2 и 3 на рисунке 5.3а) различной длины, разного диаметра, с различным набором местных сопротивлений. Так как эти трубопроводы включены последовательно, то в каждом из них имеет место один и тот же расход жидкости Q. Суммарная потеря напора для всего соединения (между точками М и N) складывается из потерь напора в каждом простом трубопроводе ( , , ), т. е. для последовательного соединения справедлива следующая система уравнений:

(5.6)

Потери напора в каждом простом трубопроводе могут быть определены через значения соответствующих расходов:

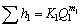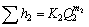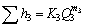; ; . (5.7)

Система уравнений (5.6), дополненная зависимостями (5.7), является основой для аналитического расчета гидросистемы с последовательным соединением трубопроводов.

Если используется графический метод расчета, то при этом возникает необходимость в построении суммарной характеристики соединения.

На рисунке 5.3б показан способ получения суммарной характеристики последовательного соединения. Для этого используются характеристики простых трубопроводов 1, 2 и 3, которые строятся по зависимостям (5.7).

Для построения точки, принадлежащей суммарной характеристике последовательного соединения, необходимо в соответствии с (5.6) сложить потери напора в исходных трубопроводах при одинаковом расходе. С этой целью на графике проводят произвольную вертикальную линию (при произвольном расходе Q'). По этой вертикали суммируют отрезки (потери напора , и ), получившиеся от пересечения вертикали с исходными характеристиками трубопроводов. Полученная таким образом точка А будет принадлежать суммарной характеристике соединения. Следовательно, суммарная характеристика последовательного соединения нескольких простых трубопроводов получается в результате сложения ординат точек исходных характеристик при данном расходе.

Параллельным называется соединение трубопроводов, имеющих две общие точки (точку разветвления и точку смыкания). Пример параллельного соединения трех простых трубопроводов приведен на рисунке 5.3в. Очевидно, что расход Q жидкости в гидросистеме до разветвления (точка М) и после смыкания (точка N) один и тот же и равен сумме расходов Q1, Q2 и Q3 в параллельных ветвях.

Если обозначить полные напоры в точках M и N через НM и HN, то для каждого трубопровода потеря напора равна разности этих напоров:

; ; ,

т. е. в параллельных трубопроводах потери напора всегда одинаковы. Это объясняется тем, что при таком соединении, несмотря на разные

гидравлические сопротивления каждого простого трубопровода, расходы Q1, Q2 и Q3 распределяются между ними так, что потери остаются равными.

Таким образом, система уравнений для параллельного соединения имеет вид

(5.8)

Потери напора в каждом трубопроводе, входящем в соединение, могут быть определены по формулам вида (5.7). Таким образом, система уравнений (5.8), дополненная формулами (5.7), является основой для аналитического расчета гидросистем с параллельным соединением трубопроводов.

На рисунке 5.3г показан способ получения суммарной характеристики параллельного соединения. Для этого используются характеристики простых трубопроводов 1, 2 и 3, которые строятся по зависимостям (5.7).

Для получения точки, принадлежащей суммарной характеристике параллельного соединения, необходимо в соответствии с (5.8) сложить расходы в исходных трубопроводах при одинаковых потерях напора.
С этой целью на графике проводят произвольную горизонтальную линию (при произвольной потере ). По этой горизонтали графически суммируют отрезки (расходы Q1, Q2 и Q3), получившиеся от пересечения горизонтали с исходными характеристиками трубопроводов. Полученная таким образом точка В принадлежит суммарной характеристике соединения. Следовательно, суммарная характеристика параллельного соединения трубопроводов получается в результате сложения абсцисс точек исходных характеристик при данных потерях.

По аналогичному методу строятся суммарные характеристики для разветвленных трубопроводов. Разветвленным соединением называется совокупность нескольких трубопроводов, имеющих одну общую точку (место разветвления или смыкания труб).

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6