микроманометр; д – двухжидкостный чашечный манометр

Рисунок 2.3 – Схемы жидкостных манометров

Пусть пьезометром необходимо измерить избыточное давление
риз6 = 0,1 МПа ≈ 1 ат в жидкости с плотностью, равной плотности воды (ρ= 1000 кг/м3). Тогда из формулы (2.3) при заданных условиях получим высоту столба воды в пьезометре Н ≈ 10 м, что является весьма значительной величиной. В машинострое-нии используются более высо-кие давления (в сотни атмосфер), что ограничивает применение пьезометров.

Аналогичные по принци-пу работы приборы с использова-нием ртути позволяют в 13,6 раза уменьшить пьезометрические высоты (ртуть в 13,6 раза тяже-лее воды). Но ртуть ядовита, и такие приборы в машинострое-нии практически перестали при-меняться.

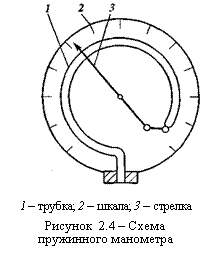
Широкое распространение в технике для измерения давлений получили пружинные маномет-ры. Основным элементом такого прибора (рисунок 2.4) является пружинящая тонкостенная трубка 1 (обычно латунная). Один из концов трубки

запаян и подвижен, а второй закреплен, и к нему подводится измеряемое давление. Подвижный конец трубки 1 кинематически связан со стрелкой 3. При изменении давления он изменяет свое положение и перемещает стрелку 3, которая указывает на соответствующее число на шкале 2.

Пружинные приборы для измерения вакуума не имеют ни принципиальных, ни конструктивных отличий от пружинных манометров. Устройства для измерения вакуума получили название вакуумметров.

Выпускаются также приборы, позволяющие измерять как избыточные давления, так и вакуум. Их принято называть мановакуумметрами.

В метеорологии измерение абсолютных значений атмосферных давлений проводят с помощью барометров. Для машиностроительных систем измерение абсолютных давлений практического значения не имеет.

2.3 Сила давления на плоскую стенку

До сих пор рассматривались давления, действующие в жидкости. Однако более важное практическое значение имеют силы, возникающие от действия жидкости на различные стенки.

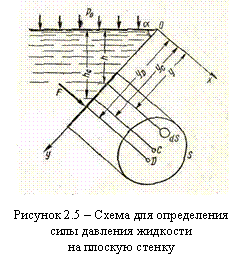При определении силы, действующей со стороны жидкости на плоскую стенку, рассмотрим общий случай, когда стенка наклонена к горизонту под углом α, а на свободную поверхность жидкости действует давление р0 (рисунок 2.5).

Вычислим силу давления F, действующую на некоторый участок рассматриваемой стенки площадью S. Ось Ох направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось Оу – перпендикулярно к этой линии в плоскости стенки.

Выразим сначала элементарную силу давления, приложенную
к бесконечно малой площадке dS:

dF = p dS = (pо + ρ gh) dS = pо dS + ρ g h d S,

где ро – давление на свободной поверхности, Па;

h – глубина расположения площадки dS, м.

Для определения полной силы F проинтегрируем полученное выражение по всей площади S:

,

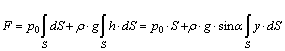где у – координата площадки dS.

Последний интеграл представляет собой статический момент площади S относительно оси Ох и равен произведению этой площади на координату ее центра тяжести (точка С), то есть

.

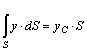Следовательно,

,

здесь hс – глубина расположения центра тяжести площади S.

Или окончательно получим

, (2.5)

т. е. полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление рС в центре тяжести этой площади.

В частном случае, когда давление ро является атмосферным
и действует также с другой стороны стенки, сила F избыточного давления жидкости на плоскую стенку равна лишь силе Fж давления от веса жидкости, т. е.

.

В общем случае давление ро может существенно отличаться от атмосферного, поэтому полную силу F давления жидкости на стенку будем рассматривать как сумму двух сил: Fо от внешнего давления pо
и силы Fж от веса жидкости, то есть

F = F0 + Fж = (pо + рС) S.

Найдем точки приложения этих сил, называемых центрами давления. Так как внешнее давление ро передается всем точкам площади S одинаково, то его равнодействующая Fо будет приложена в центре тяжести площади S. Для нахождения точки приложения силы давления Fж от веса жидкости (точка D) применим теорему механики, согласно которой момент равнодействующей силы относительно оси Ох равен сумме моментов составляющих сил, т. е.

,

где yD – координата точки приложения силы Fж.

Выражая значение Fж и dFж через величины уС и у и определяя значение yD, получаем

,

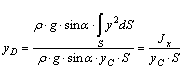где 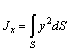– момент инерции площади S относительно оси Ох.

Учитывая, что ,

где Jxо – момент инерции площади S относительно центральной оси, параллельной Ох, находим

. (2.6)

Таким образом, точка приложения силы Fж расположена ниже центра тяжести площади стенки; расстояние между ними

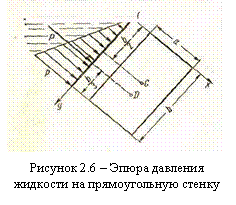
когда стенка имеет форму прямоугольника размерами а х b (рису-
нок 2.6), и одна из его сторон а лежит на свободной поверхности
с атмосферным давлением, центр давления D находится на расстоянии b/3 от нижней стороны.

2.4 Сила давления на криволинейные стенки. Плавание тел

Рассмотрим силу, действующую на криволинейную цилиндрическую стенку, которая погружена в жидкость так, что ее образующие параллельны свободной поверхности жидкости (рисунок 2.7). Такие стенки распространены на практике. В этом случае задача может быть сведена к определению равнодействующей силы, лежащей в вертикальной плоскости, перпендикулярной образующим цилиндрической поверхности. Определение этой силы сводится к определению ее вертикальной и горизонтальной составляющих.

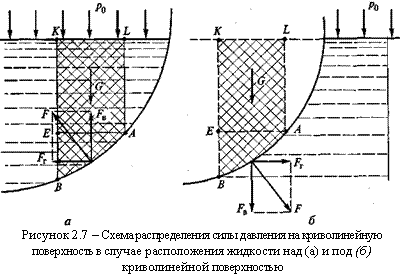В пределах цилиндрической поверхности (см. рисунок 2.7) выделим участок АВ и найдем силу F, действующую на этот участок при условии, что на свободной поверхности жидкости существует давление р0. Причем определим эту силу для двух случаев: жидкость расположена над цилиндрической поверхностью (см. рисунок 2.7а) и под ней (см. рисунок 2.7б). При определении силы, действующей на стенку, будем учитывать, что со стороны стенки на жидкость действует такая же сила, но в противоположном направлении.

Для определения силы F в первом случае (см. рисунок 2.7а) выделим объем жидкости, ограниченный поверхностью АВ и вертикальными плоскостями, проходящими через границы выбранного участка. На рисунке 2.7а

эти плоскости отображены линиями AL и ВК. Рассмотрим условия рав-новесия выделенного объема в вертикальном и горизонтальном направлениях, из которых найдем вертикальную FB и горизонтальную FГ составляющие силы F. На выделенный объем жидкости в вертикальном направлении, кроме силы FB, действуют его вес G и сила давления на свободную поверхность, равная произведению давления р0 на площадь горизонтальной проекции поверхности АВ, обозначаемую SГ . Тогда из условия равновесия найдем вертикальную составляющую

FВ = po S Г + G. (2.7)

При рассмотрении условия равновесия в горизонтальном направлении будем считать, что силы, действующие на поверхности ЕК и AL, взаимно уравновешены. Следовательно, на выделенный объем жидкости в горизонтальном направлении, кроме искомой силы F1, действует только сила давления на площадь вертикальной проекции поверхности АВ, обозначаемая SB. Ее найдем по формуле (2.4):

FГ = pC SB = (p0+hc ρ g) SВ, (2.8)

где hc – глубина погружения центра тяжести поверхности АВ, м;

SB – площадь поверхности BE, м2.

Определив по формулам (2.7) и (2.8) вертикальную FB и горизонтальную FГ составляющие силы F, найдем ее численное значение по зависимости

. (2.9)

Зависимости (2.7–2.9) получены для случая с расположением жидкости над криволинейной поверхностью. Очевидно, что при расположении жидкости снизу относительно стенки (см. рисунок 2.7б) давления в соответствующих точках будут точно такими, как и в первом случае. Поэтому
и силы, действующие на стенку (полная сила и ее вертикальная и горизонтальная составляющие), будут такими же по значению. Но направления этих сил будут противоположными, так как жидкость действует на стенку
с обратной стороны. Таким образом, формулы (2.7–2.9) будут справедливы и для этого случая. При этом в формулу (2.7) входит та же величина G, т. е. вес жидкости, которая заняла бы объем ABKL (выделен на рисунке 2.7б).

Полученные зависимости справедливы для цилиндрической поверхности, которая погружена в жидкость так, что ее образующие параллельны свободной поверхности. Аналогичным образом могут быть получены формулы для произвольной криволинейной поверхности. Их отличие будет в том, что полная сила F будет равна векторной сумме не двух составляющих сил (как в предыдущем случае), а трех. Причем одна из этих составляющих будет вертикальной, а две – горизонтальными и взаимно перпен-дикулярными.

Определение положения точки приложения силы F, действующей на криволинейную стенку, является весьма сложной задачей, которая решается с использованием графических или численных (компьютерных) методов. Определение положения точки приложения силы F, действующей на поверхность вращения (например, цилиндрическую), упрощается, так как
в этом случае линия действия силы F проходит через ось вращения поверхности.

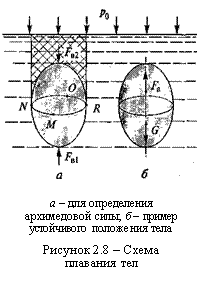Важной задачей при решении некоторых практических вопросов является определение силы, выталки-вающей тело, погруженное в жидкость. На рисунке 2.8а изображено тело произвольной формы, погруженное в жидкость. Рассмотрим силы, действующие на это тело в вертикальном направлении.

При рассмотрении сил, действующих на тело, условно разделим его замкнутой линией MNOR на две части: верхнюю и нижнюю. Причем линия разде-ления MNOR проведена так, что ее проекция и проекция тела на свободную поверхность жидкости (т. е. вертикально вверх) полностью совпадают. Обозна-чим вес жидкости, расположен-ной над телом, G0 (на рисунке 2.8а выделена штриховкой), а вес жидкости, вытесненной телом, – G, т. е. это вес жидкости, которая заняла бы объем погруженного тела (на рисунке 2.8а выделен затемнением).

Вертикальную силу (см. рисунок 2.8а), действующую на нижнюю поверхность тела, определим с использованием формулы (2.7):

FB1 = p0 SГ + G0 + G, (2.10)

где SГ – площадь горизонтальной проекции тела на свободную поверхность жидкости.

Таким же образом найдем вертикальную силу (см. рисунок 2.8а), действующую на верхнюю часть тела:

FB2 = p0 SГ + G0 . (2.11)

Их равнодействующая сила Fa , направленная вверх, будет равна алгебраической сумме этих сил и с учетом (2.10) и (2.11) определяется по формуле

.

Силу Fa принято называть архимедовой силой, а полученную для ее определения зависимость – законом Архимеда [1–3,9,10], согласно которому на тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх и равная весу жидкости, вытесненной телом.

Точкой приложения этой силы является геометрический центр тела, который называется центром водоизмещения. Он может не совпадать
с центром тяжести тела. Эти центры совпадают, если тело состоит из однородного и равномерно распределенного вещества. Плавающее тело будет находиться в устойчивом равновесии, когда центр водоизмещения располагается выше центра тяжести тела и они лежат на одной вертикальной прямой (см. рисунок 2.8б).

2.5 Относительный покой жидкости

Под относительным покоем понимают неподвижное состояние жидкости относительно сосуда, который движется с постоянным ускорением. Например, в относительном покое может находиться жидкость в емкости, которая установлена на разгоняющейся транспортной машине (топливный бак автомобиля). В относительном покое будет также находиться жидкость в сосуде, вращающемся с постоянной скоростью.

Законы, действующие при относительном покое жидкости, принципиально не отличаются от ранее рассмотренных законов гидростатики. Но если в ранее рассмотренных случаях на жидкость действовала только одна массовая сила – сила тяжести, то при относительном покое появляется новая – сила инерции. Это приводит к изменению положения свободной поверхности жидкости и изменению давлений в различных ее точках.

Анализ относительного покоя удобно проводить для сил, действующих на условную частицу жидкости единичной массы (массой т = 1). При таком подходе сила всегда численно равна соответствующему ускорению. Например, на частицу единичной массы действует сила тяжести
G = mg =1 g = g. Таким образом, математические зависимости существенно упрощаются.

Рассмотрим прямолинейное движение сосуда с постоянным ускорением (или замедлением) а. В этом случае на каждую частицу жидкости единичной массы действуют две силы: сила тяжести g и сила инерции а (рисунок 2.9). Равнодействующая этих двух сил

(2.12)

определяет положение свободной поверхности жидкости, так как угол
между этой поверхностью и силой всегда составляет 90°. Из геометрических

соображений (см. рисунок 2.9) следует, что положение свободной поверхности может быть задано углом α, значение которого найдем из отношения

tga = а/g.

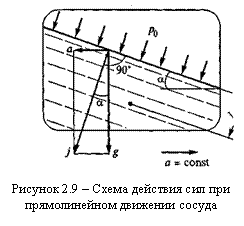Для определения давле-ния в произвольно выбранной точке на расстоянии l от сво-бодной поверхности исполь-зуется математическая зависимость

p = p0 + l ρ j. (2.13)

Она получена тем же методом, что и основное уравнение гидростатики, но учитывает действие не только сил тяжести, но и сил инерции.

Эта зависимость являя-ется более общей, чем основной закон гидростатики, который может быть получен из нее как частный случай. Действительно, при а = 0 из (2.12) следует j = g. Тогда
c учетом l = h из (2.13) получим формулу (2.1), т. е. основное уравнение гидростатики.

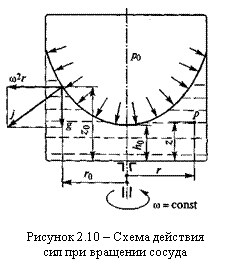Другим случаем отно-сительного покоя жидкости является вращение сосуда с постоянной угловой скоростью ω (рисунок 2.10). При вращении на каждую частицу жидкости единичной массы, располо-женную на радиусе r, также действуют две силы: сила тяжести g и сила инерции, вызванная центробежным ус-корением, а = ω2 r. Равнодействующая этих двух сил

определяет положение свобод-ной поверхности жидкости. Но
в рассматриваемом случае цент-робежное ускорение является переменной величиной, так как зависит от радиуса расположения точки.

Поэтому поверхность вращения принимает параболическую форму и описывается уравнением

,

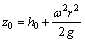где z0 – высота расположения точки свободной поверхности относительно дна сосуда;

h0 – высота жидкости на оси вращения.

Формула для определения давления р в любой точке жидкости может быть получена методом, использованным в 2.1.

Тогда после математических преобразований найдем давление в точке, расположенной на радиусе r и высоте z относительно дна сосуда:

. (2.14)

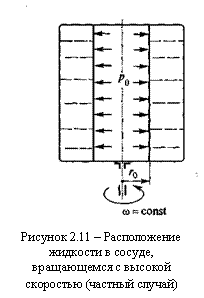
На практике часто встречается другой частный случай – вращение сосуда с очень высокой скоростью. В этом случае центробежные силы существенно больше сил тяжести и жидкость отбрасывается центробежными силами к стенкам сосуда (рисунок 2.11), а ее свободная поверхность располагается на радиусе r0. Тогда некоторыми геометрическими величинами, входящими в формулу (2.12), можно пренебречь и формула для определения давления упрощается:

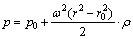. (2.15)

Следует отметить, что формула (2.14) получена для сосуда, имеющего вертикальную ось вращения, а формула (2.15) применима для вращающихся сосудов с любым расположением оси в пространстве.

3 КИНЕМАТИКА И ДИНАМИКА ЖИДКОСТИ

3.1 Основные понятия и определения

Уравнения кинематики и динамики жидкости весьма значительно отличаются от аналогичных уравнений для твердого тела. Это вызвано, прежде всего, особенностями исследуемого объекта – жидкости, частицы которой не имеют жесткой связи между собой. Отсутствие жесткой связи существенно усложняет рассмотрение процессов, происходящих в жидкости. Для упрощения изучения течений в гидромеханике широко используется так называемая идеальная жидкость. Под этим термином понимают гипотетическую несжимаемую жидкость, в которой отсутствуют силы межмолекулярного взаимодействия, то есть отсутствует вязкость. Тогда происходящие явления сначала исследуются применительно к идеальной жидкости, а затем полученные закономерности переносятся с введением корректирующих поправок на потоки реальных жидкостей.

Течение жидкости, как и любое другое движе-ние, может быть устано-вившимся и неустановив-шимся. Установившимся называется течение, при котором все физические параметры (скорость, давление и другие) зависят только от координат точки и остаются неизменными во времени, то есть

р = f1 (х,y,z), υ = f2 (х,y,z), .

Примером установившегося течения может служить истечение через отверстие в дне сосуда, в котором поддерживается постоянный уровень жидкости, или движение жидкости в трубопроводе, создаваемое центробежным насосом с постоянной частотой вращения вала.
В частном случае установившееся течение может быть равномерным, когда скорость каждой частицы не изменяется с изменением ее координаты и поле скоростей остается неизменным вдоль потока. При неустановившемся течении физические параметры потока (или некоторые из них) изменяются в пространстве и во времени. В общем случае

неустановившегося течения давление и скорость зависят как от координат, так и от времени: р = F1 (х,y,z,τ), v = F2 (х,y,z,τ). Для примера можно привести рассматриваемое выше истечение, но без поддержания постоянного уровня жидкости в сосуде, то есть истечение до полного опорожнения или в напорной трубе поршневого насоса, поршень которого совершает возвратно-поступательное движение. В дальнейшем будут рассматриваться в основном установившиеся течения жидкости.

Для описания движения в механике жидкости существуют разные подходы, в которых рассматриваются различные модели сплошной среды [5,6,7] и соответствующие им уравнения движения (Коши,
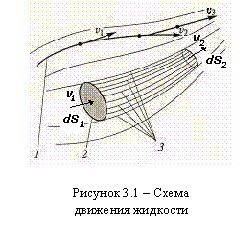
Эйлера и другие). В машиностроительной гидравлике поток жидкости принято представлять как совокупность элементарных замкнутых объемов, движущихся совместно. Большое значение в этой модели имеет понятие «линия тока». Под этим термином понимают условную линию в потоке жидкости, проведенную так, что вектор скорости в любой ее точке направлен по касательной (линия 1 на рисунке 3.1). При установившемся течении линия тока совпадает с траекторией движения частицы жидкости. Необходимо также отметить, что при установившемся течении в любой точке потока существует только одна (неизменная во времени) скорость. Поэтому через данную точку может проходить только одна линия тока. Следовательно, линии тока при установившемся течении не могут пересекаться.

Если в потоке жидкости взять бесконечно малую замкнутую линию 2 (см. рисунок 3.1), состоящую из множества точек, и через каждую из этих точек провести линию тока 3, то множество этих линий образуют трубчатую поверхность. Такую поверхность принято называть трубкой тока, а часть потока внутри этой поверхности – элементарной струйкой.

Как было отмечено ранее, при установившемся течении линии тока не пересекаются и, следовательно, ни одна линия тока не может пронизывать трубку тока (иначе она пересечет одну из линий, образующих эту трубку). Следовательно, ни одна частица жид­кости не может проникнуть внутрь трубки тока или выйти из нее. Таким образом, выделенная трубка тока при установившемся течении является непроницаемой стенкой для жидкости.

Сечениями потока (или струйки) жидкости принято называть поверхности, нормальные к линиям тока. Например, поверхность dS1, ограниченная замкнутым контуром 2 (затемнена на рисунке 3.1), является сечением для элементарной струйки. При параллельно-струйном течении сечения представляют собой плоскости, перпендикулярные

направлению движения жидкости. Сечения потоков или струй жидкости иногда также называют живыми сечениями.

Различают напорные и безнапорные течения жидкости. Напорными называют течения в закрытых руслах без свободной поверхности, а безнапорными – течения со свободной поверхностью. Примерами напорного течения могут служить течения в трубопроводах, гидромашинах, гидроаппаратах. Безнапорными являются течения в реках, открытых каналах. В данном учебном пособии рассматриваются
в основном напорные течения жидкости.

3.2 Расход. Уравнение расхода

Расход – это количество жидкости, которое протекает через данное сечение в единицу времени. Количество жидкости можно измерять в единицах объема, массы или веса. Поэтому различают объемный Q (м3/с), массовый QM (кг/с) и весовой QG (Н/с) расходы.

Для элементарной струйки, имеющей бесконечно малые площади сечений, можно считать скорость υ одинаковой во всех точках сечения. Следовательно, объемный расход для элементарной струйки

dQ = υ dS.

Основываясь на законе сохранения вещества и полагая, что течение внутри элементарной струйки является сплошным и неразрывным, можно утверждать, что для установившегося течения несжимаемой жидкости

dQ = υ1 dS1 = υ2 dS2 = const. (3.1)

Это уравнение называется уравнением объемного расхода для элементарной струйки.

Для потока конечных размеров скорость в общем случае имеет различные значения в разных точках сечения, поэтому расход определяют как сумму элементарных расходов струек, составляющих поток:

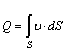. (3.2)

На практике удобнее определять расход через среднюю по сечению потока скорость

υср = Q / S,

откуда

Q = υср ·S.

Очевидно, что и для потока конечных размеров при условии его сплошности и неразрывности будет выполняться условие постоянства объемного расхода вдоль потока, то есть

Q = υср1 ·S1 = υср2 ·S2 = const. (3.3)

Из последнего уравнения следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям сечений

. (3.4)

Полученные уравнения расходов (3.1) и (3.3) являются следствием общего закона сохранения вещества.

3.3 Уравнение Бернулли для элементарной

струйки идеальной жидкости

Рассмотрим установившееся течение элементарной струйки идеальной жидкости, находящейся под действием лишь одной массовой силы – силы тяжести (рисунок 3.2). В рассматриваемом случае в жидкости могут действовать нормальные напряжения сжатия (давление), но не могут действовать касательные напряжения (трение), так как у жидкости отсутствует вязкость.

Для вывода уравнения Бернулли выберем два сечения 1–1 и 2–2,
а также произвольную горизонтальную поверхность О–О. Будем считать, что в сечении 1–1 площадью dS1 скорость жидкости υ1 и действует давление р1, а его центр тяжести располагается на высоте z1 относительно выбранной поверхности 0–0. Сечение 2–2 характеризуется аналогичными параметрами, но с индексом «2» (dS2, υ2, р2 и z2).

Пусть за время dτ участок струйки, ограниченный сечениями 1–1 и 2–2, сдвинулся и занял новое положение, ограниченное сечениями 1'–1' и 2'–2'. Тогда первое сечение переместилось на расстояние dl1, а второе сечение – на расстояние dl2. При этом можно условно считать, что часть ограниченного объема жидкости осталась на месте (объем между сечениями 1–1 и 2–2), а другая часть между сечениями 1–1
и 1'–1' (на рисунке 3.2 заштрихована) переместилась на место между сечениями 2–2 и 2'–2' (на рисунке 3.2 также заштрихована), т. е. объемы заштрихованных участков равны:

.

Следовательно, равны и массы этих объемов (dm), а также одинаковы их веса (dG).

Для вывода уравнения Бернулли применим к жидкому телу, находящемуся между сечениями 1–1 и 2–2, теорему механики об изменении кинетической энергии, согласно которой изменение кинетической энергии тела равно работе сил, приложенных к этому телу.

Как следует из сказанного ранее, кинетическая энергия участка жидкости между сечениями 1'–1' и 2–2 за время dτ не изменилась, так как этот участок условно можно считать неподвижным. Тогда изменение кинетической энергии всего жидкого тела будет определяться разностью кинетических энергий выделенных объемов (участков, затемненных на рисунке 3.2), а точнее, изменением их скоростей, так как их массы одинаковы, т. е.

.

Работу за отмеченный промежуток времени совершают силы тяжести и силы давления. При оценке работы сил тяжести также будем учитывать условную неподвижность участка жидкости между сечениями 1'–1' и 2–2. Тогда работа сил тяжести AG определится перемещением веса dG на расстояние (z1 – z2):

AG =dG (z1 – z2).

Работа сил давления Ap будет складываться из двух величин: работы положительной силы и работы отрицательной силы. Первая, равная произведению давления pl на площадь dS1, способствует сдвигу сечения 1–1 на расстояние dl1, а вторая, равная произведению давления р2 на площадь dS2, препятствует перемещению сечения 2–2 на расстояние dl2, то есть

.

Приравняв сумму работ сил тяжести AG и давления Ap к изменению кинетической энергии тела Ек, получим

.

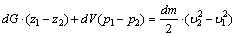Разделим каждый член последнего уравнения на вес dG. После математических преобразований, учитывая, что dG = dm·g = dV·ρ·g, получим

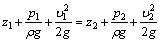, (3.5)

где z – геометрический напор, м;

р / ρ·g – пьезометрический напор, м;

υ2 / 2g – скоростной напор, м.

Полученное уравнение называется уравнением Бернулли [1–3,9,10] для элементарной струйки идеальной жидкости. Оно было получено Даниилом Бернулли в 1738 году.

Трехчлен вида

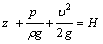
называется полным напором.

Уравнение Бернулли (3.5) записано для двух произвольно выбранных сечений. Очевидно, что для любого другого сечения этой же струйки полный напор будет иметь то же значение:

.

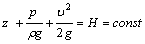Таким образом, для идеальной движущейся жидкости сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная вдоль струйки.

3.4 Геометрическая и энергетическая иллюстрация

уравнения Бернулли

Рассмотрим элементарную струйку идеальной жидкости, показанную на рисунке 3.3. Измерим величины геометрического, пьезометрического и скоростного напоров в сечениях 1–1, 2–2 и 3–3.

Как видно из рисунка, сумма трех напоров, представляющая собой полный напор, во всех сечениях будет одинакова, а линия полного напора параллельна произвольной горизонтальной плоскости сравнения, то есть тоже горизонтальна. Если соединить поверхности жидкости в пьезометрах, установленных вдоль потока плавной линией, то получим геометрическое место точек, называемое пьезометрической линией.

напор увеличивается в 16 раз, а сечение 3– 3 имеет ту же площадь, что и сечение 1–1. Штриховой линией показана пьезометрическая линия при увеличении расхода еще в раз, вследствие чего скоростные высоты увеличиваются в два раза, а в узкой части струйки давление становится меньше атмосферного, т. е. возникает вакуум.

Уравнение Бернулли можно записать в другой форме. Помножив уравнение (3.5) на ускорение свободного падения g, получим

. (3.6)

Рассмотрим энергетический смысл уравнения Бернулли, записанный в форме (3.6). Условимся называть удельной энергией жидкости энергию, отнесенную к единице массы.

Нетрудно показать, что члены этого уравнения являются различными формами удельной механической энергии жидкости, а именно:

gz – удельная потенциальная энергия положения;

р/ρ – удельная потенциальная энергия давления движущейся жидкости;

υ2/2 – удельная кинетическая энергия жидкости;

– полная удельная механическая энергия движущейся жидкости.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6