Таким образом, энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве полной удельной энергии жидкости вдоль струйки. Следовательно, уравнение Бернулли выражает закон сохранения механической энергии в идеальной жидкости. Механическая энергия движущейся жидкости может иметь три формы: энергия положения, давления и кинетическая энергия. Первая и третья формы механической энергии известны из механики, и они в равной степени свойственны твердым и жидким телам. Энергия давления является специфической для движущихся жидкостей и газов. В процессе движения идеальной жидкости одна форма энергии может превращаться в другую, однако полная удельная энергия при этом, как следует из уравнения Бернулли, остается без изменений.

Как всякая форма энергии, энергия давления легко преобразу-ется в механическую работу. Прос-тейшим устройством, с помощью которого осуществляют такое пре-образование, является цилиндр
с поршнем (рисунок 3.4). При подаче жидкости под давлением в левую полость цилиндра поршень со штоком будет перемещаться вправо, преодолевая усилие, приложенное к штоку, таким образом совершать полезную работу.

3.5 Уравнение Бернулли для потока реальной жидкости

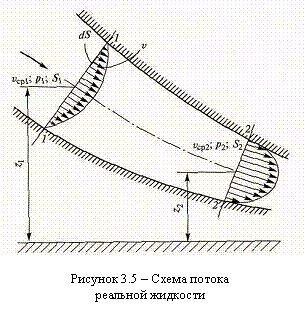
Пусть поток реальной жидкости, обладающей вязкостью, движется в русле, ограниченном неподвижными стенками. При этом вследствие трения между слоями жидкости существенно возрастает неравномерность распределения скоростей по сечению потока (рисунок 3.5),
а также возникают потери энергии на трение при перемещении жидкости от одного сечения к другому. Кроме того, движение вязкой жидкости часто сопровождается вращением частиц, вихреобразованием
и перемешиванием, что тоже требует затрат энергии. Поэтому удельная

энергия движущейся вязкой жидкости не остается постоянной, как
в случае идеальной жидкости, а постепенно расходуется на преодоление сопротивлений, и, следовательно, уменьшается вдоль потока.

Получим уравнение Бернулли для потока реальной жидкости, основываясь на том, что оно является законом сохранения энергии для движущейся жидкости. Вывод этого уравнения проведем в два этапа. На первом этапе учтем неравномерность распределения скоростей по сечению потока, а на втором учтем и потери энергии.

При выводе будем считать, что в пределах выбранных сечений гидростатический напор остается постоянным:

. (3.7)

На первом этапе определим формулу для вычисления мощности N потока реальной жидкости в его сечении. Вычисление этого параметра затруднено тем, что из-за перераспределения скоростей (см. рисунок 3.5) разные слои жидкости несут различное количество энергии.

Для определения мощности N в сечении (например, в сечении 1–1 на рисунке 3.5) выберем струйку жидкости бесконечно малой поперечной площади dS, в пределах которой скорость жидкости будем считать постоянной, равной υ. Тогда полный напор (или полная удельная энергия) в сечении струйки

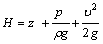. (3.8)

Мощность струйки dN в сечении площадью dS равна произведению удельной энергии Н и веса жидкости, которую проносит поток через это сечение в единицу времени, т. е. элементарного весового расхода dQG. Тогда с учетом (3.6) и (3.1) получим математическую зависимость для мощности струйки:

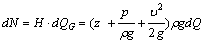. (3.9)

Мощность всего потока в сечении найдем, просуммировав мощности всех элементарных струек, т. е. вычислив интеграл по площади S от выражения (3.9):

.

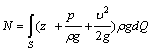После математических преобразований зависимость для мощности потока реальной жидкости принимает следующий вид:

, (3.10)

где α – безразмерный коэффициент, определяемый по формуле

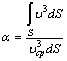. (3.11)

Этот коэффициент, называемый коэффициентом Кориолиса, учитывает неравномерность распределения скорости жидкости в сечении реального потока. Если числитель и знаменатель в формуле (3.11) умножить на величину ρ/2, то станет очевидно, что коэффициент α есть отношение действительной кинетической энергии реального потока
в данном сечении к кинетической энергии того же потока в том же сечении, но посчитанной по средней скорости жидкости в данном сечении. В этом заключается физический смысл коэффициента Кориолиса.

Алгебраическое выражение, ограниченное скобками в (3.10), принято называть средним значением полного напора в сечении реального потока, т. е.

. (3.12)

Средний напор Нср широко используется в практических расчетах, так как является важнейшим параметром, характеризующим механическую энергию (или мощность) потока реальной жидкости. Для подтверждения этого решим уравнение (3.10) относительно Hср с учетом (3.12). Тогда получим

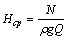. (3.13)

Из анализа зависимости (3.13) следует, что при постоянном расходе Q средний напор Hср пропорционален мощности N и в пределах данного потока однозначно определяет эту мощность. Поэтому средний напор Hср, вычисляемый с учетом неравномерности распределения скоростей в сечении по формуле (3.12), в дальнейшем будем использовать в качестве основного параметра, характеризующего механическую энергию потока реальной жидкости.

Учтем теперь потери энергии, возникающие при движении жидкости. В реальных потоках из-за этих потерь среднее значение полного напора в конечном сечении всегда меньше, чем в начальном сечении, т. е. H ср1 > H ср2. Поэтому при записи уравнения баланса энергий (средних напоров) в его правую часть добавляют слагаемое , учитывающее потери удельной энергии. Тогда уравнение баланса принимает вид 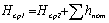, или с учетом (3.12)

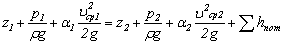. (3.14)

Уравнение (3.14) носит название уравнения Бернулли для потока реальной жидкости [1–3, 5–7].

Сравним уравнение Бернулли для струйки идеальной жидкости (3.6) и уравнение для потока реальной жидкости (3.14). Из этого сравнения следует, что в последнем уравнении дополнительно присутствуют коэффициент Кориолиса α и .

При равномерном распределении скоростей по сечению потока

α = 1 (поток идеальной жидкости). В потоках реальной жидкости
коэффициент Кориолиса в большинстве случаев лежит в пределах

1 < α < 2.

Суммарная потеря полного напора на участке между начальным и конечным сечениями складывается из суммы потерь удельной энергии во всех гидравлических сопротивлениях, расположенных на рассматриваемом участке потока. В гидравлике эти потери энергии принято делить на две группы: местные потери и потери на трение по длине.

Местные потери hм – это потери в так называемых местных гидравлических сопротивлениях, к которым относятся поворот, сужение или расширение потока, а также различные гидравлические устройства (вентили, жиклеры и т. д.). Потери в большинстве этих сопротивлений вызваны вихреобразованием. Как показывает практика, они пропорциональны квадрату скорости жидкости, а для оценки их величины используется формула Вейсбаха

, (3.15)

где ζ – безразмерный коэффициент, определяющий потери в данном местном сопротивлении;

υср – средняя скорость в трубопроводе, в котором установлено местное сопротивление, м/с.

Второй вид гидравлических потерь – потери на трение по длине hтр – это потери, которые имеют место в длинных прямых трубах постоянного сечения. Потери на трение по длине вызваны как внутренним трением в жидкости, так и трением о стенки трубы. Эти потери пропорциональны длине трубы l и обратно пропорциональны ее диаметру d. Они имеют достаточно сложную зависимость от средней скорости жидкости, (это будет рассмотрено позднее), но во всех случаях для их оценки может быть использована универсальная для гидравлики формула Дарси

, (3.16)

где λ – безразмерный коэффициент потерь на трение по длине, который принято называть коэффициентом Дарси.

Следует отметить, что определение потерь энергии при расчете гидравлических систем является одной из наиболее важных проблем гидравлики.

3.6 Примеры использования уравнения Бернулли в технике

Уравнение Бернулли широко применяется в технике, как для выполнения гидравлических расчетов, так и для решения ряда практических задач. Одной из таких задач является измерение скорости и расхода жидкости. Рассмотрим некоторые устройства для измерения расхода и скорости жидкости.

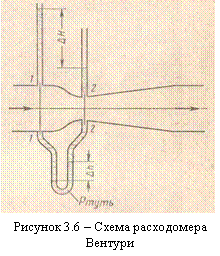
Расходомер Вентури представляет собой устройство, устанавливаемое в трубопроводах и осуществляющее сужение потока – дросселирование (рисунок 3.6). Расходомер состоит из двух участков – плавно

венно υ2, р2, S2. Разность показаний пьезометров, присоединенных
к указанным сечениям, ΔН.

Запишем для сечений 1–1 и 2–2 потока уравнение Бернулли
и уравнение расхода (считая распределение скоростей равномерным):

где hм – потеря напора между сечениями 1–1 и 2–2.

Учитывая, что и найдем из этой системы уравнений одну из скоростей, например

,

отсюда объемный расход

(3.17)

или , (3.18)

где С – величина, постоянная для данного расходомера.

Зная величину С и наблюдая за показанием пьезометра, можно найти расход в трубопроводе для любого момента времени по формуле (3.18). Константу С можно определить теоретически, но точнее ее можно найти экспериментально, т. е. в результате градуирования расходомера.

Связь между ΔН и Q получается параболической, а если по оси абсцисс откладывать расход во второй степени, то график этой зависимости будет представ-

лять собой прямую.

Очень часто вместо пары пье-зометров для из-мерения перепада давления в расхо-домере применяют

дифференциальный ртутный манометр. Учитывая, что над ртутью в трубках находится та же жидкость плотностью ρ, можно записать

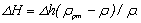
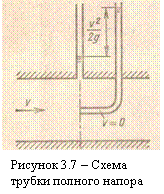
Трубка полного напора (или трубка Пито) служит для измерения скорости, например, в трубе (рисунок 3.7). Если установить в этом потоке трубку, изогнутую под углом 90°, отверстием навстречу по-току и пьезометр, то жидкость в этой трубке поднимается над уровнем

в пьезометре на высоту, равную скоростному напору. Объясняется это тем, что скорость υ частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, а давление, следовательно, увеличивается на величину скоростного напора. Измерив разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке.

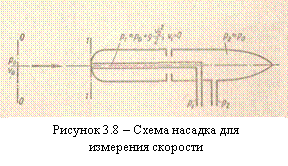
На этом же принципе основано измерение скорости полета самолета. На рисунке 3.7 показана схема самолетной скоростной трубки (насадка) для измерения малых по сравнению со скоростью запуска скоростей полета.

Запишем уравнение Бернулли для струйки, которая набегает на трубку вдоль ее оси, а затем растекается по ее поверхности. Для сечений 0–0 (невозмущенный поток) и 1–1 (где υ = 0), получаем

.

Так как боковые отверстия трубки приближенно воспринимают давление невозмущенного потока, р2 ≈ р0, следовательно, из предыдущего имеем

.

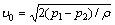Другим важным случаем практического использования уравнения Бернулли является создание топливно-воздушной смеси для двигателей внутреннего сгорания с помощью карбюратора и эжектора.

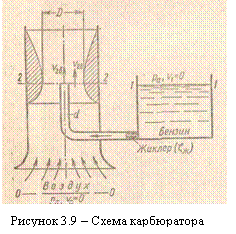
Карбюратор поршневых двигателей внутреннего сгорания служит для подсоса бензина и смешения его с потоком воздуха (рисунок 3.9).

сопротивления воздушного канала (до сечения 2–2) ζв и жиклера ζж (сопротивлением бензотрубки пренебрегаем).

Записав уравнение Бернулли для потока воздуха (сечение 0–0 и
2–2), а затем для потока бензина (сечение 1–1 и 2–2), получим (при
z1 = z2 и α = 1):

,

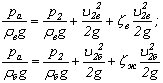откуда

.

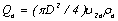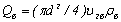Учитывая, что массовые расходы и , получим

.

Таким образом обеспечивается постоянство соотношения расходов бензина и воздуха. Однако следует иметь в виду приближенный характер данного решения.

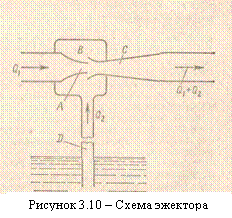
Струйный насос (эжектор) состоит из плавно сходящегося насадка А (рисунок 3.10), осущест-вляющего сжатие потока, и постепенно расширяющейся трубки С, установленной на некотором расстоянии от насадка в камере В. Вследствие увеличения скорости потока давление в струе на выходе из насадка и по всей камере В значительно понижается. В расширяющейся трубке скорость уменьшается, а давление возрастает приблизительно до атмосферного (если жидкость вытекает в атмосферу), следовательно, в камере В давление обычно меньше атмосферного, т. е. возникает разрежение (вакуум). Под действием разрежения жидкость из нижнего резервуара всасывается по трубе D в камеру В, где происходят слияние и дальнейшее перемешивание двух потоков.

3.7 Режимы течения жидкости в трубах

Опыты показывают, что возможны два режима или два вида течения жидкостей и газов в трубах: ламинарный и турбулентный [1–3, 5–10].

Указанные течения жидкости можно наблюдать на приборе, представленном на рисунке 3.11. Он состоит из резервуара А с водой, от которого отходит стеклянная труба В с краном С на конце, и сосуда D с индикаторной подкрашенной жидкостью, которая может по трубке вводиться тонкой струйкой внутрь стеклянной трубы В.

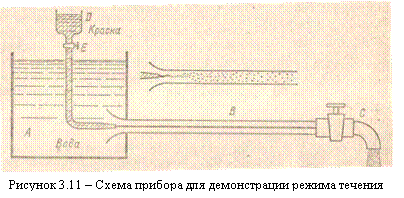Если несколько приоткрыть кран С и дать возможность воде протекать в трубе с небольшой скоростью, а затем с помощью крана Е впустить индикаторную жидкость в поток воды, то увидим, что введенная в трубу подкрашенная жидкость не будет перемешиваться
с потоком воды. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубы, что указывает на слоистый характер течения жидкости и на отсутствие перемешивания. Пьезометр или трубка Пито, присоединенные к трубе, покажут неизменность давления и скорости по времени, отсутствие колебаний (пульсаций). Это так называемое ламинарное (слоистое) течение.

При постепенном увеличении скорости течения воды в трубе путем открытия крана С картина течения вначале не меняется, но затем при определенной скорости течения наступает быстрое ее изменение. Струйка подкрашенной жидкости при выходе из трубки начинает колебаться, затем размываться и перемешиваться с потоком воды, причем становятся заметными вихреобразования и вращательное движение жидкости. Пьезометр и трубка Пито показывают непрерывные пульсации давления и скоростей в потоке воды. Течение становится, как его принято называть, турбулентным (см. рисунок 3.11, вверху).

Если уменьшить скорость потока, то восстановится ламинарное течение.

Итак, ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсаций скоростей и давления. При таком течении все линии тока определяются формой русла, по которому течет жидкость. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, т. е. прямолинейно; отсутствуют поперечные перемещения жидкости.

Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. При турбулентном течении векторы скоростей имеют не только осевые, но и нормальные составляющие, поэтому наряду с основным продольным перемещением жидкости вдоль русла происходят поперечные перемещения (перемешивание) и вращательное движение отдельных объемов жидкости.

Режим течения данной жидкости в данной трубе изменяется при вполне определенной средней по сечению скорости течения υ кр, которую называют критической. Как показывают опыты, значение этой скорости прямо пропорционально кинематической вязкости v и обратно пропорционально диаметру трубы d, т. е.

.

Входящий в эту формулу безразмерный коэффициент пропорциональности k одинаков для всех жидкостей и газов, а также для любых диаметров труб. Это означает, что изменение режима течения происходит при определенном соотношении между скоростью, диаметром и вязкостью v:

k = υкр d/v.

Полученное безразмерное число называется критическим числом Рейнольдса и обозначается

Reкр = υкр d/v. (3.19)

Критическое число Рейнольдса Reкр не зависит от рода жидкости и размеров сечения, а лишь в небольшой степени определяется формой сечения и шероховатостью стенок трубы.

Таким образом, критическое число Рейнольдса является критерием, определяющим режим течения в трубах.

Как показывают опыты, для труб круглого сечения Reкр ≈ 2300.

Зная скорость движения жидкости, ее вязкость и диаметр трубы, можно расчетным путем найти число Re и, сравнив его с Reкр , определить режим течения жидкости [1–3].

При Re < Reкр течение является ламинарным, при Re > Reкр – турбулентным. Точнее говоря, вполне развитое турбулентное течение

в трубах устанавливается лишь при значениях Re ≥ 10000, а при

2300 ≤ Re ≤ 10000 имеет место переходная, критическая область.

На практике имеют место как ламинарное, так и турбулентное течения, причем первое наблюдается в основном в тех случаях, когда по трубам движутся весьма вязкие жидкости, например смазочные масла, второе обычно происходит в водопроводах, а также в трубах, по которым перетекают бензин, керосин, спирты, кислоты и другие маловязкие жидкости.

3.8 Теория ламинарного течения в круглых трубах

Как указывалось ранее, ламинарное течение является строго упорядоченным, слоистым течением без перемешивания жидкости. Теория ламинарного течения жидкости основывается на законе трения Ньютона. Это трение между слоями движущейся жидкости является единственным источником потерь энергии в данном случае.

Рассмотрим установившееся ламинарное течение жидкости
в прямой круглой цилиндрической трубе с внутренним диаметром
d = 2r0. Чтобы исключить влияние силы тяжести и этим упростить вывод, допустим, что труба расположена горизонтально. Достаточно далеко от входа в нее, где поток уже вполне сформировался (стабилизировался), выделим отрезок длиной l между сечениями 1–1 и 2–2.

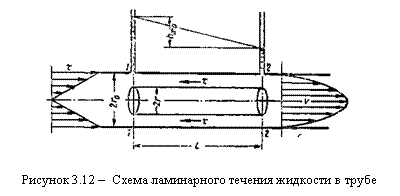Пусть в сечении 1–1 давление равно р1, а в сечении 2–2 – р2. Ввиду постоянства диаметра трубы, скорость жидкости будет постоянной,
а коэффициент а будет неизменным вдоль потока вследствие его стабильности, поэтому уравнение Бернулли для выбранных сечении примет вид

,

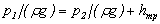где hтр – потеря напора на трение по длине, м.

Отсюда

,

что и показывают пьезометры, установленные в этих сечениях.

В потоке жидкости выделим цилиндрический объем радиусом r, соосный с трубой и имеющий основания в выбранных сечениях. Запишем уравнение равномерного движения выделенного объема жидкости в трубе, т. е. равенство нулю суммы сил, действующих на объем: сил давления и сопротивления. Обозначая касательное напряжение на боковой поверхности цилиндра через τ, получим

,

откуда

.

Из формулы следует, что касательные напряжения в поперечном сечении трубы изменяются по линейному закону в функции радиуса. Эпюра касательного напряжения показана на рисунке 3.12 слева.

Выразим касательное напряжение τ по закону трения Ньютона через динамическую вязкость и поперечный градиент скорости;
при этом заменим переменное (расстояние от стенки) у текущим радиусом r:

.

Знак минус обусловлен тем, что направление отсчета радиуса r (от оси к стенке) противоположно направлению отсчета расстояния у (от стенки).

Подставляя значение τ в предыдущее уравнение, получаем

.

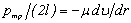Найдем отсюда приращение скорости

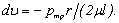
При положительном приращении радиуса получается отрицательное приращение (уменьшение) скорости, что соответствует профилю скоростей, показанному на рисунке 3.12.

Выполнив интегрирование, получим

Постоянную интегрирования С найдем из условия, что на стенке при r = r0 υ = 0:

,

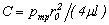тогда скорость по окружности радиусом r

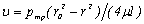. (3.20)

Это выражение является законом распределения скоростей по сечению круглой трубы при ламинарном течении. Кривая, изображающая эпюру скоростей, является параболой второй степени.

Максимальная скорость, имеющая место в центре сечения (при r = 0),

. (3.21)

Входящее в формулу (3.20) отношение pтр/l (см. рисунок 3.12) представляет собой гидравлический (пьезометрический) уклон, умноженный на ρg. Эта величина является постоянной вдоль прямой трубы постоянного диаметра.

Применим полученный закон распределения скоростей, описываемый уравнением (3.20) для расчета расхода. Для этого выразим сначала элементарный расход через бесконечно малую площадку dS:

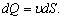
Здесь есть функция радиуса, определяемая формулой (3.20),
а площадку dS целесообразно взять в виде кольца радиусом r и шириной dr, тогда

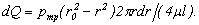
После интегрирования по всей площади поперечного сечения, т. е. от r = 0 до r = r0, получим

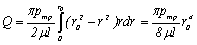. (3.22)

Среднюю по сечению скорость найдем делением расхода на площадь. С учетом выражения (3.22) получим

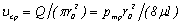. (3.23)

Сравнение этого выражения с формулой (3.20) показывает, что средняя скорость при ламинарном течении в два раза меньше максимальной: .

Для получения закона сопротивления, т. е. выражения потери напора hтр на трение через расход и размеры трубы, определим pтр из формулы (3.22)

Разделив это выражение на произведение ρg, заменив величину динамической вязкости µ на произведение νρ, а величину pтр на произведение hтрρg, а также перейдя от радиуса r0 к диаметру d = 2r0, найдем

(3.24)

Полученный закон сопротивления показывает, что при ламинарном течении в трубе круглого сечения потеря напора на трение пропорциональна расходу и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закон, обычно называемый законом Пуазейля, используется для расчета трубопроводов с ламинарным течением [1–3,9,10].

Заменим в формуле (3.24) расход произведением После сокращений получим

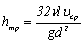. (3.25)

Данное выражение известно как закон Стокса [1,9]. Приведем закон сопротивления Стокса к виду формулы Вейсбаха-Дарси:

.

Для этого умножим и разделим формулу (3.25) на скорость, перегруппировав сомножители, после сокращений получим

,

откуда следует, что при ламинарном режиме

. (3.26)

где λл – коэффициент потерь на трение для ламинарного течения.

Изложенная теория ламинарного течения жидкости в круглой трубе хорошо подтверждается опытом, и выведенный закон сопротивления обычно не нуждается в каких-либо поправках, за исключением следующих случаев:

1) при течении в начальном участке трубы, где происходит постепенное формирование параболического профиля скоростей;

2) при течении с теплообменом;

3) при течении в капиллярах и зазорах с облитерацией;

4) при течении с большими перепадами давления.

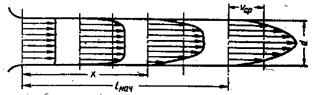
Участок от начала трубы, на котором формируется (стабилизируется) параболический профиль скоростей, называется начальным участком течения (lнач). За пределами этого участка имеем стабилизированное ламинарное течение, параболический профиль скоростей остается неизменным, как бы ни была длинна труба, при условии сохранения ее прямолинейности и постоянства сечения. Изложенная выше теория ламинарного течения справедлива именно для этого стабилизированного ламинарного течения и неприменима в пределах начального участка.

Для определения длины начального участка можно пользоваться приближенной формулой Шиллера, выражающей эту длину, отнесенную к диаметру трубы, как функцию числа Re:

. (3.27)

Сопротивление на начальном участке трубы получается больше, чем на последующих участках. Объясняется это тем, что значение производной dυ/dy у стенки трубы на начальном участке больше, чем на участках стабилизированного течения, а потому больше и касательное напряжение, определяемое законом Ньютона, и притом тем больше, чем ближе рассматриваемое сечение к началу трубы, т. е. чем меньше координата x.

Потеря напора на участке трубы, длина которого l lнач, определяется по формуле

. (3.28)

Закономерности ламинарного течения с теплообменом и большими перепадами давления подробно рассмотрены в [1].

3.9 Турбулентное течение

3.9.1 Основные сведения

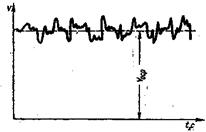
Турбулентное течение характеризуется перемешиванием жид-кости, пульсациями скоростей и давлений. Если с помощью особо

чувствительного прибора-самописца измерить и записать пульсации, например, скорости по времени в фиксированной точке потока, то получим картину, подобную показанной на рисунке 3.14. Скорость беспорядочно колеблется около некоторого осредненного по времени значения υоср, которое в данном случае остается постоянным.

Рисунок 3.14 – Пульсация скорости в турбулентном потоке

Траектории частиц, проходящих через данную неподвижную точку пространства в разные моменты времени, представляют собой кривые линии различной формы, несмотря на прямолинейность трубы. Характер линий тока в трубе в данный момент времени также отличается большим разнообразием (рисунок 3.15).

Рисунок 3.15 – Характер линий тока в турбулентном потоке

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6